基于SST的无砟轨道离缝缺陷识别方法研究

杨 勇，田秀淑，赵维刚，杨怀志

(1.石家庄铁道大学 安全工程与应急管理学院,河北 石家庄 050043；2.石家庄铁道大学 材料科学与工程学院, 河北 石家庄 050043；3.京沪高速铁路股份有限公司,北京 100005)

无砟轨道是我国高速铁路的主要轨道结构型式，受环境荷载和列车荷载的长期、反复作用，因此由轨道板、功能层、支承层和支承结构构成的无砟轨道结构不可避免的在不同部位显现不同类型、不同程度的病害。其中，轨道板与功能层之间的离缝缺陷是无砟轨道的常见病害形式[1]。由于离缝缺陷早期发育于无砟轨道结构内部，表观无法直观观测。随着离缝缺陷进一步发展，离缝面积逐步增加，导致轨道板与功能层不断摩擦，引发功能层浆液流出、无砟轨道结构外部封闭层混凝土碎裂等病害，这些病害将破坏无砟轨道结构传力路径，严重影响列车行驶的平顺性和安全性[2]。所以，研究无砟轨道离缝缺陷检测方法，及早发现无砟轨道结构内部是否存在离缝缺陷和离缝缺陷的发育状态，已成为我国高速铁路无砟轨道结构状态检测的重要研究内容。

无砟轨道是由多层混凝土构成的层状结构。目前，层状混凝土结构内部缺陷检测方法主要包括探地雷达法、超声波法和弹性波法。

探地雷达法通过分析电磁波在不同介电常数物质表面的反射波和透射波，获取结构内部状态。探地雷达在混凝土目标检测中的主要对象为钢筋[3]和空洞[4]。但是无砟轨道钢筋分布密集，Yang等[5-6]分析了探地雷达B-Scan回波特征，提出基于曲波变换的方向滤波器，实现了无砟轨道中空洞缺陷定位与识别，但这种方法适用于平面面积大、竖向尺度厚的缺陷识别，对于竖向小尺寸离缝缺陷检测识别的有效性还有待研究。

超声波法是根据超声波在被检测目标内的传播时间和幅值变化判断缺陷位置和大小。梁咏宁等[7]分析了硅酸盐对混凝土的侵蚀作用，得到了混凝土强度与超声波传播速度之间的关系。林韦正等[8]运用超声波法检测了混凝土中的裂缝。但这些方法适用于浅层、大目标、强反射混凝土结构内部目标，难以适应小尺度离缝缺陷检测需求。

弹性波法是混凝土结构内部缺陷的常用手段，其主要通过弹性回波信号的Fourier频谱分析，获取无砟轨道结构结构状态[9-10]。但实际检测信号中，常伴随着检测装置的系统噪声、环境噪声和边界噪声，Fourier频谱分析难以有效分辨无砟轨道离缝回波。

近年来，随着调和分析的发展，时频分析方法逐步应用于结构病害检测信号处理。Epp等[11]运用小波变换处理钢筋混凝土结构弹性回波信号，识别内部空洞缺陷；Chang等[12]结合FFT和Morlet小波变换提出钢筋回波和裂缝回波的区分方法。小波时频分析方法被证明是奇异点检测的有效手段，但是其频域分辨率较低，基于此，Daubechies等[13]、Auger等[14]提出同步挤压小波变换(Synchrosqueezing Wavelet Transform,SST)，其将有利于提高多目标回波的分辨率。因此，本文提出将SST方法用于无砟轨道离缝回波信号处理，以期提升离缝缺陷的识别精度。

1 弹性波离缝缺陷识别原理

1.1 无砟轨道结构模型与弹性波传播特性分析

1.1.1 无砟轨道结构弹性波传播模型

无砟轨道是由轨道板、功能层、支承层和路基表层等支承结构构成的多层复合结构。图1为无砟轨道结构模型。图1中，E、ρ、μ分别为材料的动态弹性模量、材料密度、泊松比。

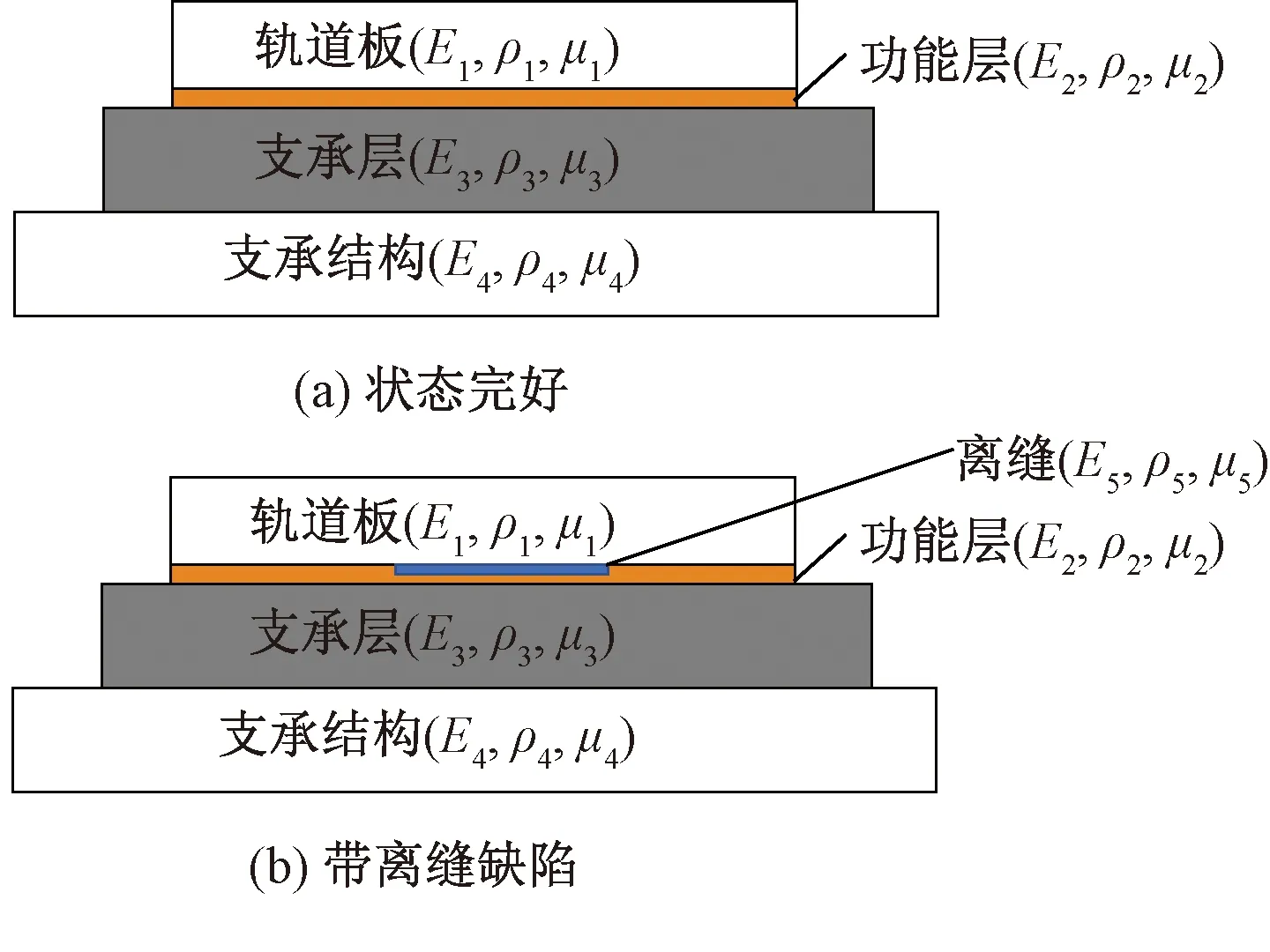
图1 无砟轨道复合结构模型

弹性波在无砟轨道内部传播过程中由于各层波阻抗的不同，将在不同介质表面产生弹性波的反射和透射现象。以垂直入射的P波为例，其反射系数R和透射系数T分别为

(1)

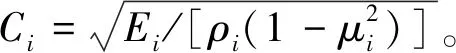
图2为CRTSⅡ型无砟轨道弹性波P波的传播特性。在状态完好的无砟轨道结构中，由于无砟轨道复合结构各层的波阻抗不同，特别是在轨道板与功能层界面，弹性波将发生反射和折射，在支承层与路基表层界面，由于波阻抗差异巨大，绝大部分的能量将发生反射，极小部分发生透射。而CRTSⅡ型无砟轨道功能层较薄(约为3 cm)，轨道板与功能层界面回波和功能层与支承层界面回波混叠，所以图2中忽略了轨道板与功能层之间的界面回波。

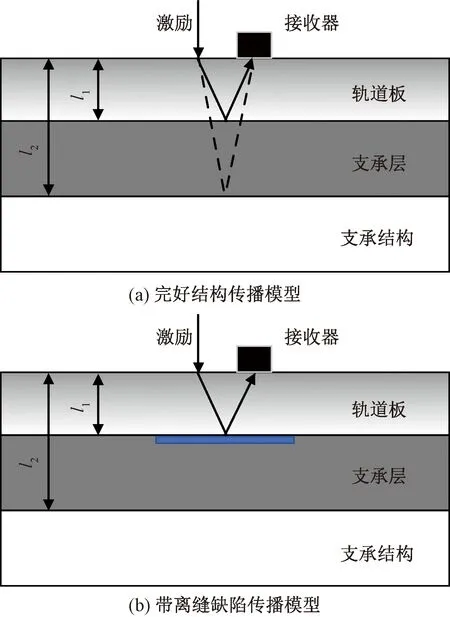
图2 无砟轨道弹性波理想传播模型

设轨道板厚度为l1，轨道板、功能层和支承层的总厚度l2，则接收器接收的回波信号中存在两种显著频率信号f1和f2，即

f1=C1/2l1f2=C2/2l2

(2)

式中：C1和C2分别为传播路径的平均波速。

在带离缝缺陷的无砟轨道结构中，由于功能层离缝与轨道板在波阻抗上的巨大差异，其反射系数R约等于1，P波将不再向下传播，所以接收器接收的回波信号显著频率只包含式(2)中的f1。

1.1.2 无砟轨道回波时频分析

设激励输入信号为u(t)为有限支撑信号，其支撑区间与激励形状和激励-轨道板表面接触时间相关。弹性波在无砟轨道中传播时伴随着能量衰减，设在轨道板中的能量衰减系数为α1，在轨道板和支承层平均衰减系数为α2，则轨道板与功能层(离缝缺陷)反射回波信号可表示为

(3)

式中：R1为轨道板与功能层界面反射系数；t1=2l1/C1；符号*为运算符，表示卷积运算；n为反射次数，n=1,2,3,…；δ为单位脉冲函数。

支承层与支承结构反射回波信号可表示为

(4)

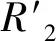
当结构状态完好时，回波信号x(t)表示为

x(t)=x1(t)+x2(t)

(5)

当结构带离缝缺陷时，回波信号x(t)表示为

x(t)=x1(t)

(6)

为计算方便，将激励信号u(t)简化为常量u0，则x1(t)和x2(t)的Fourier变换X1(f)和X2(f)可表示为

(7)

由此可见，X1(f)和X2(f)的幅值在n/t1和n/t2(n=1,2,3,…)处呈现脉冲信号，且幅值大小近似与频率f成反比。即由x1(t)和x2(t)组合形成的完好结构回波信号在f1=1/t1和f2=1/t2呈现较强的频域峰值；带离缝缺陷结构的回波信号将只在f1=1/t1存在频域峰值。

1.2 同步挤压小波时频分析

1.2.1 常用回波信号处理方法

基于FFT的回波信号频率特征分析，是判断无砟轨道离缝缺陷的常规途径。设结构回波信号为x(t)，其Fourier频谱为

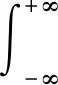
(8)

但实测信号中包含了设备系统噪声、环境噪声和边界噪声。图3显示了实测无砟轨道冲击回波信号与信号的Fourier谱。从图3(a)可知接收器接收的回波信号包含了冲击响应、系统噪声和余振噪声等多种回波成分，而图3(b)中频谱成分复杂，并不能明确获知无砟轨道界面回波信号。

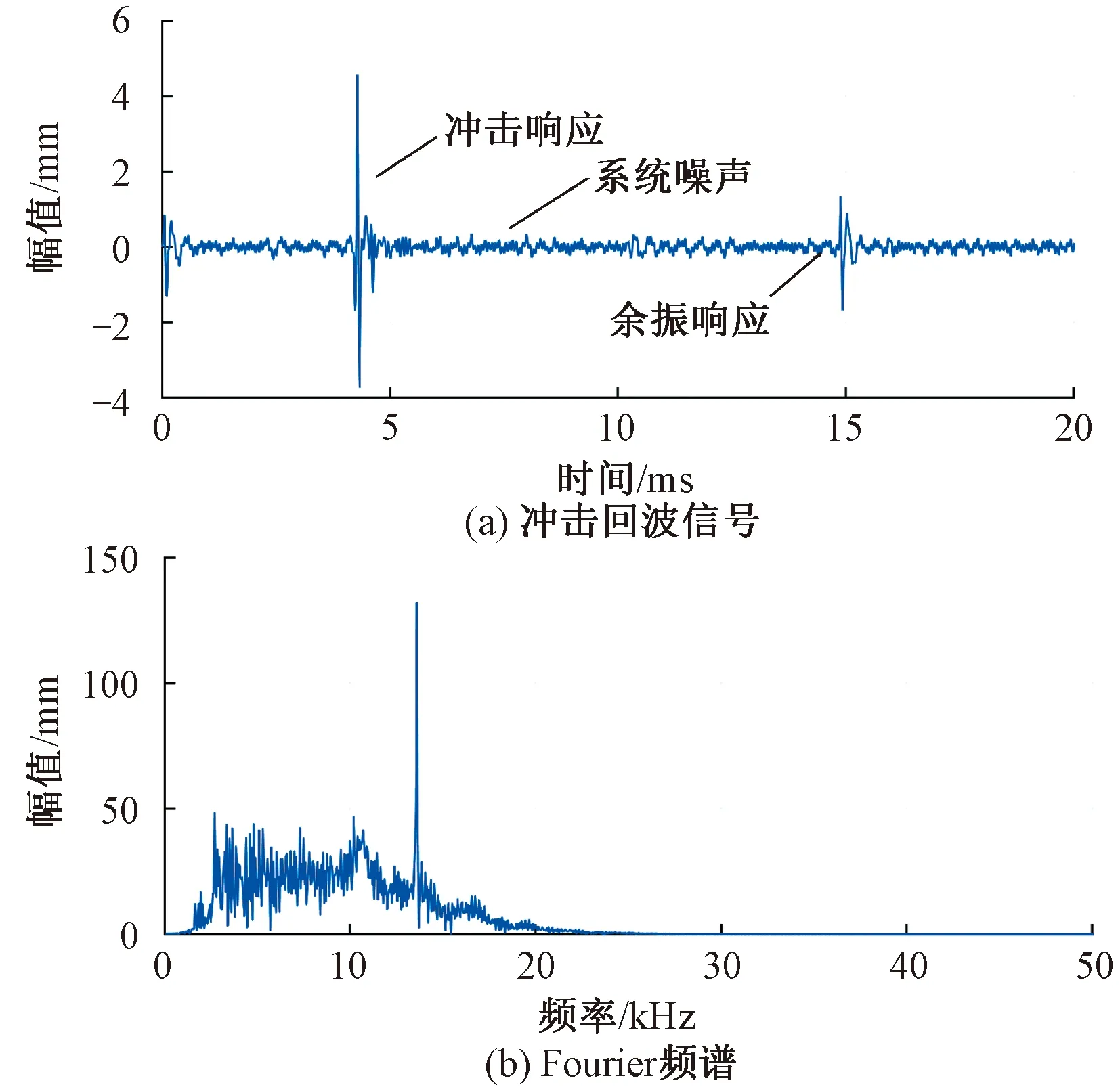
图3 实测无砟轨道冲击回波信号与Fourier谱

1.2.2 同步挤压小波变换(SST)

SST是由Daubenchies等[15]于2011年在总结了STFT和小波变换的缺点基础上，结合Hilbert-Huang经验模态分解提出的一种提高时频分辨率的信号分析方法，SST的处理过程主要分为信号的连续小波变换、小波时间-尺度空间到时间-频率空间转换和时频空间同步挤压三个步骤。

设x(t)为时域信号，则x(t)的连续小波变换Wx(a,b)可表示为

(9)

式中：a为尺度参数；b为时间参数；φ*为母小波函数的复共轭。

通常，小波变换用1/a近似表示频率f，尺度参数a值越大，小波母函数的支撑区间越大，对应频率f越低；a值越小，小波母函数的支撑区间越小，对应频率f越高。

但尺度参数与数据频率之间的物理意义并不明确，需将时间-尺度空间转换为时间-频率空间。设信号x(t)是由N个频率分量组合形成，即

(10)

式中：xi(t)=Aicos(2πfit)，Ai为第i个信号幅值，fi为xi(t)的频率。

根据Plancherel定理，xi(t)分量的连续小波变换可表示为

Wxi(a,b)=

(11)

式中：Xi(f)和Φ(f)分别为x(t)和φ(t)的傅里叶变换。

对Wxi(a,b)相对于时间参数b求导数，可得到瞬时频率fi，即

(12)

根据式(12)可将(b,a)平面转换为(b,f)平面。此时，以fi为中心，以Δfi/2为半径，对周围的非零值同步压缩，即SST表示为Txi(f,b)，计算式为

(13)

式中：Δfi=fi-fi-1。

图4为信号x(t)=Acos[2π(t+1)2]的小波变换和同步挤压过程。信号的瞬时频率f=2t+2，采样频率为100 Hz，采样时间10 s。图4(b)中连续小波变换纵坐标采用了对数坐标，所以图中瞬时频率显示为曲线。对比小波变换和SST变换，很明显，以时间为函数的瞬时频率在连续小波变换中被模糊化，频率分辨率降低；在SST变换中，以瞬时频率为中心，通过对连续小波变换的积分挤压，频率成分向中心频率集中，分辨率明显提高。

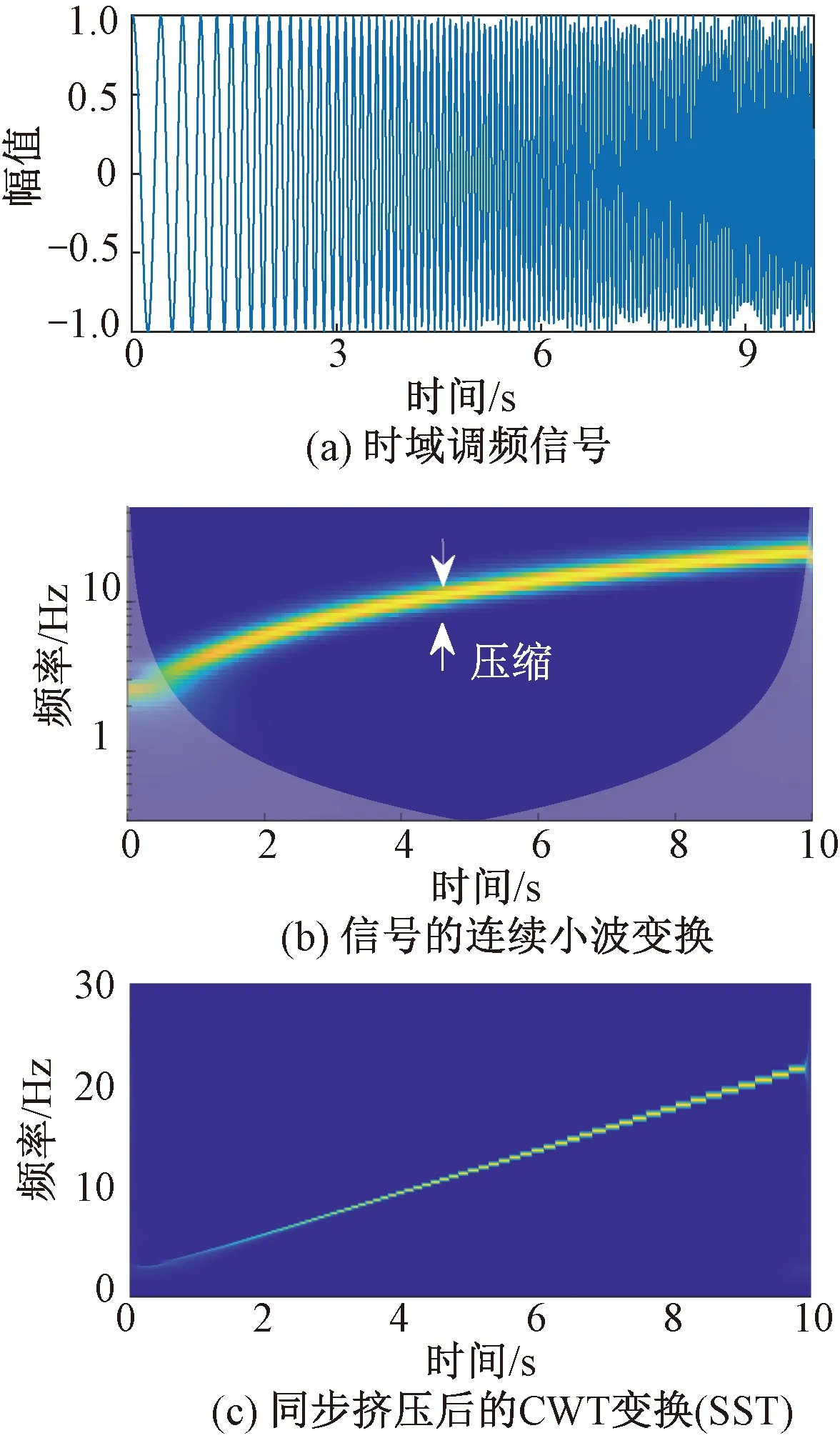
图4 SST变换过程示意图

综上所述，SST变换作为一种高分辨率时频分析方法，将有利于区分轨道板与支承层界面回波和支承层与支承结构的界面回波，提高高速铁路无砟轨道离缝缺陷检测精度。

2 数值模拟与试验分析

为验证SST在实际无砟轨道离缝缺陷检测识别中的应用效果，本文从数值仿真模拟、现场试验出发分析了所提方法的有效性。

2.1 数值模拟试验

(1) 数值试验模型

本文运用Ansys有限元分析软件构建CRTSⅡ型无砟轨道三维数值仿真模型。CRTSⅠ型无砟轨道结构轨道板、支承层和支承结构的仿真参数和数值采样参数如表1和表2所示，无砟轨道结构边界采用完美匹配层作为弹性波的吸收层。

表1 数值仿真模型参数

表2 数值采集参数

数值仿真模型如图5所示。图5(b)中离缝缺陷的长度为50 cm。

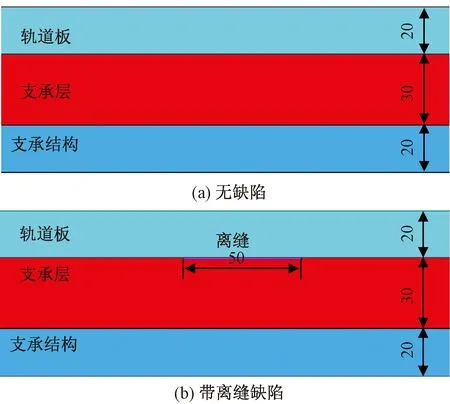
图5 数值仿真模型(单位：cm)

(2) 试验分析

数值仿真弹性波传播过程如图6所示。其中图6(a)、图6(b)为弹性波在无缺陷无砟轨道结构中的传播过程。当t=1.13×10-4s时，弹性波穿过了轨道板和支承层的界面，透射P波波头进入支承层，如图6(a)所示。由于支承层和轨道板波阻抗分别为9.36×106、8.03×106kg/(m2·s)，反射率R=0.076，透射率T=0.924，反射波能量很少，几乎不可见。

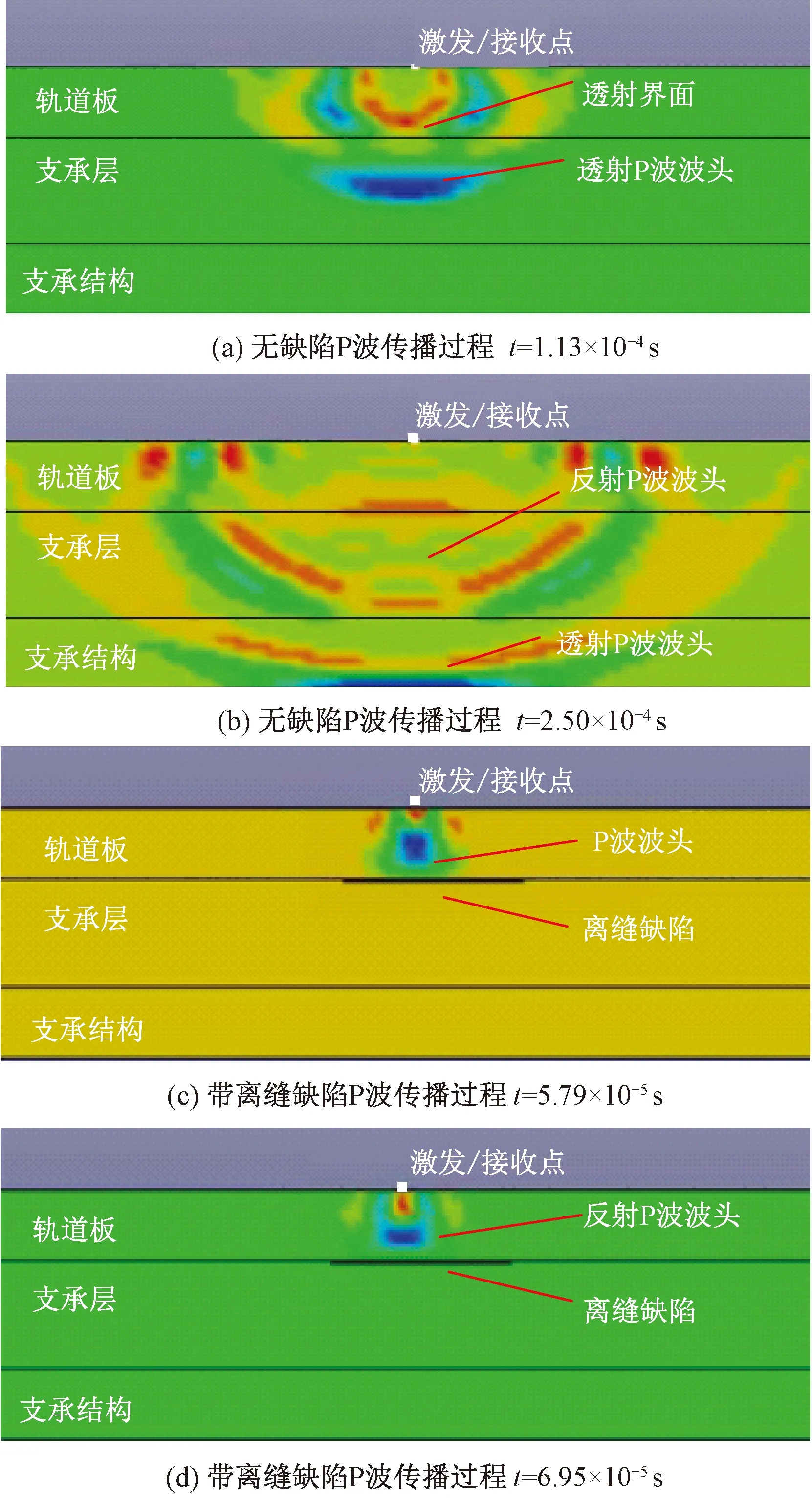
图6 弹性波传播过程

当t=2.50×10-4s时，如图6(b)所示，此时透射P波波头到达支承层底部，由于支承层与支承结构波阻抗差异，支承层与支承结构的反射P波波头清晰可见。

图6(c)、图6(d)为弹性波在带离缝缺陷无砟轨道结构中的传播过程。从图6(c)可见，当t=5.79×10-5s时，P波波头到达轨道板与离缝缺陷界面。图6(d)显示了当t=6.95×10-5s时，P波的传播状态。此时，由于离缝缺陷与轨道板波阻抗的巨大差异，所有的P波信号均被反射，没有透射的P波信号。

无缺陷、带离缝缺陷无砟轨道速度回波信号见图7。由图7(a)可见，由于轨道板与支承层密切接触，且波阻抗接近，大部分能量向下传播，所以回波信号衰减速度快。由图7(b)可见。由于缺陷的存在，反射率R=1，所以相对于无缺陷回波，离缝缺陷回波幅值较大，且幅度衰减速度明显变慢。

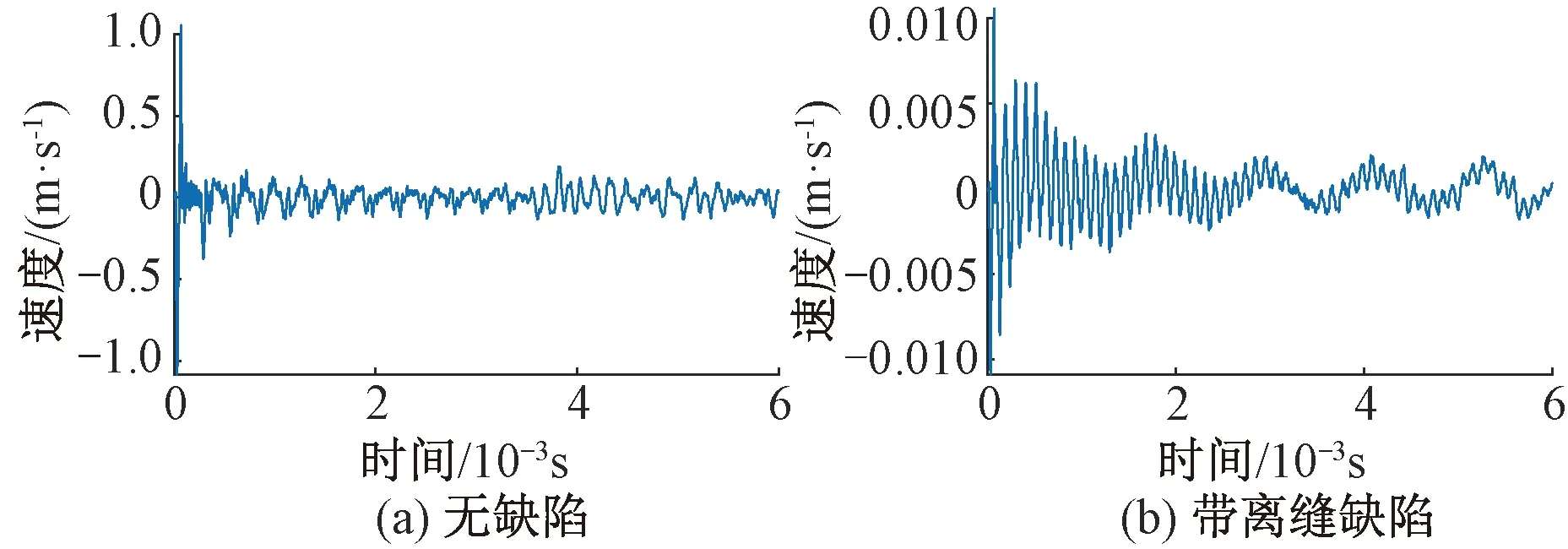
图7 无缺陷、带离缝缺陷无砟轨道速度回波信号

对图7速度回波信号进行SST处理，处理结果如图8所示。图8(a)为无缺陷无砟轨道速度回波信号的SST变换。从图8(a)中可以看出，在0～4 ms之间存在明显的支承层与支承结构之间的界面回波，频率约为3.55 kHz，与计算频率3.58 kHz基本相符。同时，无缺陷无砟轨道速度回波信号的SST变换在7.20、11.00 kHz附近出现了较强的幅值，为周期脉冲回波信号频谱。而轨道板和支承层边界的回波频谱并不明显。从图8(b)中可以看出，在0～6 ms之间存在非常显著的轨道板与离缝缺陷界面回波，频率约为9.50 kHz，与计算频率9.75 kHz基本相符。

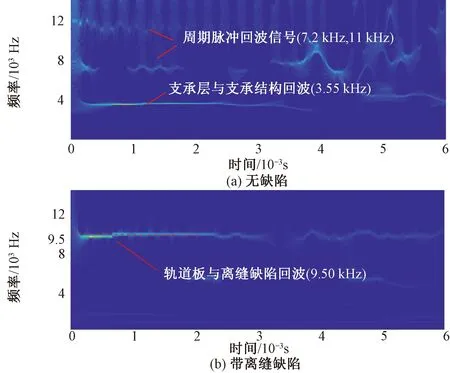
图8 无砟轨道回波信号SST变换

2.2 现场试验

现场试验分别对没有浇筑功能层的空板、含预设缺陷的CRTSⅢ型无砟轨道板和CRTSⅡ型运营线路无砟轨道离缝缺陷展开测试。现场试验传感器采用BK4533-B-002型加速度传感器，采样频率为200 kHz，激励方式为锤击方式。

(1) 空板试验

波速是影响弹性波回波频率分布的重要因素。空板试验是为了获取轨道板与支承层完全脱离时，轨道板底部的回波频率，进而获取其弹性波的波速信息。

试验采用CRTSⅢ型无砟轨道结构，轨道板厚度为20 cm。图9为试验采集到的数据和SST处理结果。经过SST变换后，空板状态下轨道板底部回波信号的显著频率在12 kHz附近，轨道板弹性波P波波速约为4 800 m/s。同时，图9(c)显示在20～30 kHz之间存在明显幅值信号，为轨道板边界、承轨台边界回波噪声。

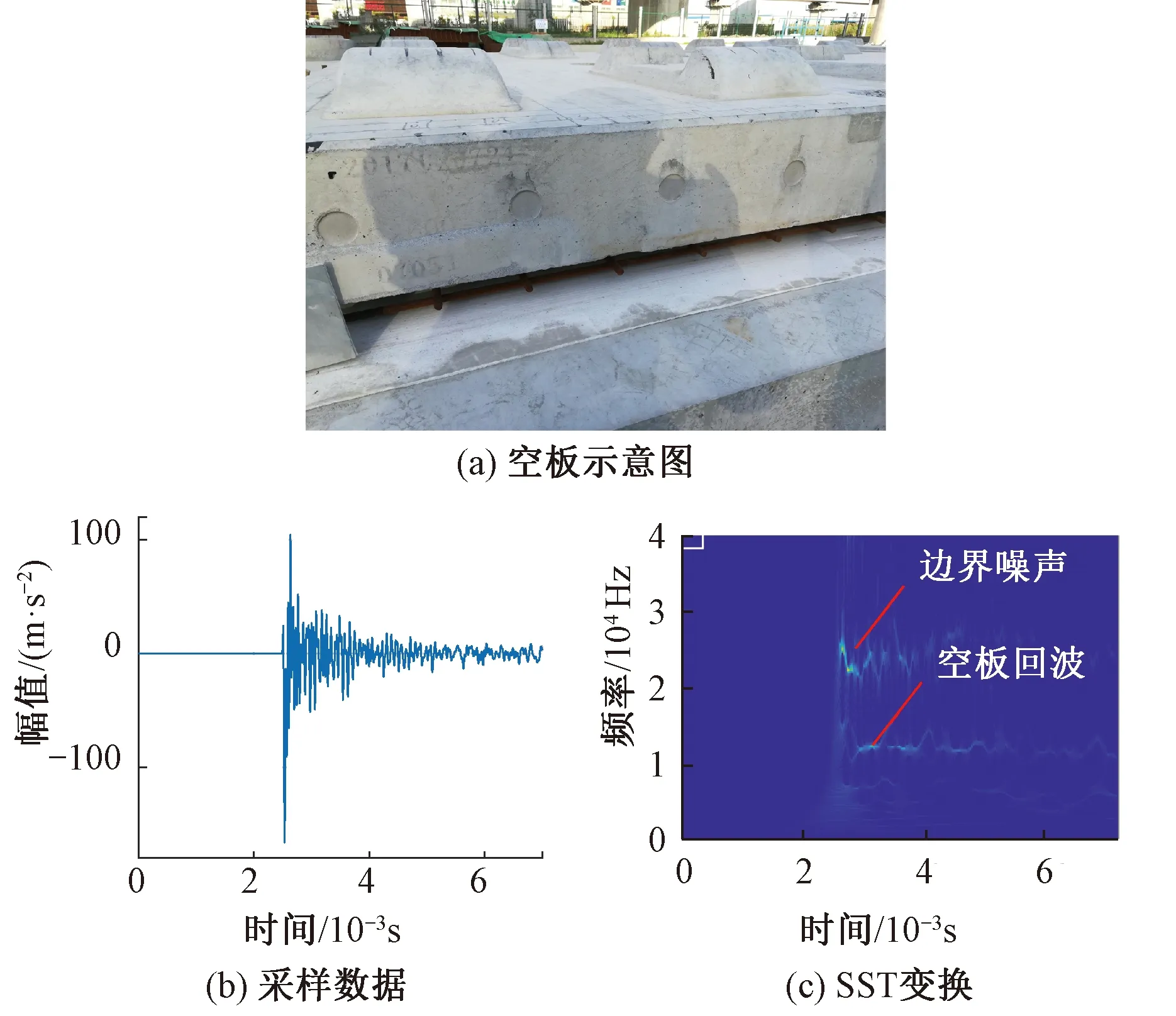
图9 空板试验

(2) 预设缺陷试验

预设缺陷位置为CRTSⅢ型无砟轨道结构轨道板底部，预设缺陷采用泡沫胶带，尺寸为10 cm × 10 cm。试验过程中数据采集点分别设在轨道板表面预设缺陷中心位置和远离预设缺陷位置。图10为预设缺陷示意，图11为两次采集到的回波数据。

图10 预设缺陷示意(单位：cm)

由图11可见，当采集点为病害中心位置时，回波显著频率以12 kHz为主，即由于泡沫胶带与轨道板在弹性模量上的巨大差异，弹性波P波以反射回波为主，与空板检测显著频率吻合。当采集点远离预设缺陷时，回波频率以6.8 kHz频率为主。由于试验对象为CRTSⅢ型无砟轨道，功能层厚度为9 cm，此时功能层厚度不能再忽略不计；同时，由于混凝土凝固时间较短，检测时功能层并没有完全达到设计强度，造成了功能层和支承层之间弹性模量的差异，影响了弹性波波速，所以回波显著频率在6.8 kHz附近达到峰值。

图11 预设缺陷采集数据与SST变换

由此可见，运用SST能够有效的区分无砟轨道内部有无离缝缺陷。

(3) 运营线路无砟轨道离缝缺陷检测试验

2017年，本文作者所在课题组在CRTSⅡ无砟轨道运营线路上进行了弹性波离缝缺陷检测试验，传感器测点布置如图12所示。

图12 运营线路试验测点布置

以图中测点5—测点16为测试范围，测点间距为20 cm。测试过程中传感器以双面胶的形式黏结固定。SST处理结果如表3所示。

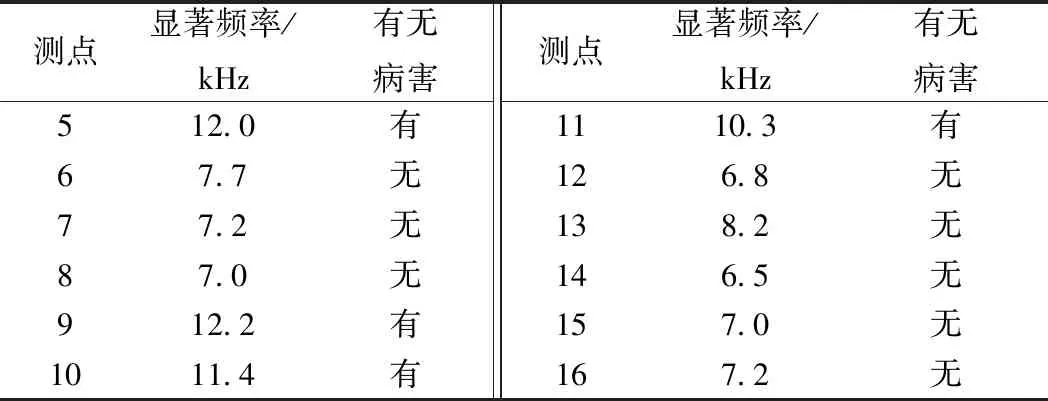
表3 运营线路测试处理结果

对表3的处理结果可用云图进行表示，如图13所示。显然，在轨道板中部位置存在比较明显的离缝缺陷。在横向测线1和3的边缘部分，离缝缺陷正处于发育状态。

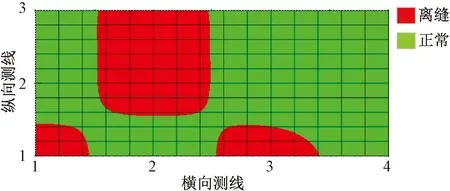
图13 运营线路离缝缺陷检测结果云图

2.3 分析与讨论

2.3.1 与FFT的对比分析

FFT为常用的弹性波信号分析方法。为对比SST和FFT对离缝缺陷的检测精度，对图11(a)、图11(b)所示的不同采集点数据进行FFT变换，如图14所示。从图14中可以看出，图14(a)和图14(b)分别在12.7、6.8 kHz出现了频域峰值，分别表示预设缺陷回波和无缺陷支承层回波。同时图14(a)在7 kHz附近仍有代表支承层回波的频域峰值，与1.1.1节所述带离缝缺陷弹性波传播模型不符，造成无砟轨道离缝缺陷判识困难。

图14 预设缺陷数据FFT变换

由图11(c)、图11(d)可以清楚的看出回波信号显著频率开始时间和持续时长，这将有利于判断无砟轨道结构中是否存在离缝缺陷。

2.3.2 对系统噪声的抑制作用

噪声信号干扰了无砟轨道离缝缺陷的判识精度。如图15(a)所示，为无砟轨道离缝缺陷检测数据采集信号，对该信号进行FFT变换处理，如图15(b)所示。显然，分别在f1=3.52 kHz和f2=10.25 kHz存在两个显著频率，如根据1.1.2小节分析，直接从Fourier频谱上判断该处为正常状态的无砟轨道。

该信号的SST变换结果如图15(c)所示。从接收传感器接收到激励信号形成的信号起跳点前后，系统中一直存在着3.52 kHz的系统噪声，而起跳点后，回波信号的显著频域只有存在于10 kHz左右，所以此处应为存在离缝缺陷的无砟轨道。

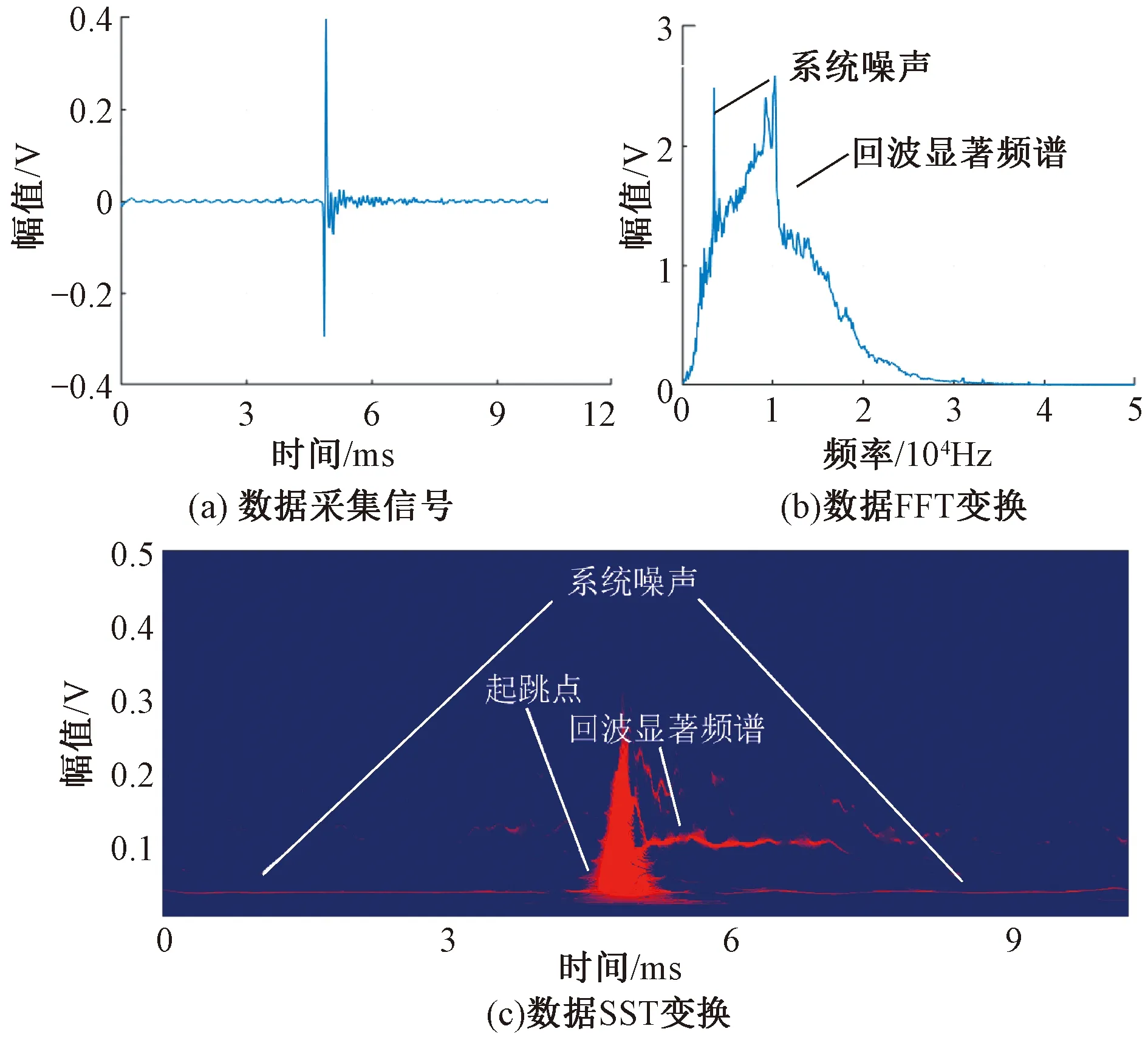
图15 噪声抑制对比

由此可见，运用SST变换可有效抑制采集设备的系统噪声，提高回波频域成分识别精度。

3 结论

本文分析了弹性波在无砟轨道中的传播特性，解析了无砟轨道不同状态条件下弹性波回波的频率特征，提出基于SST的无砟轨道离缝缺陷识别方法，得出如下结论：

(1) 无砟轨道是否存在离缝缺陷在频谱上表现出不同的显著性特征。状态完好的无砟轨道理论上存在两个显著频率，实际处理过程中，由于轨道板与支承层波阻抗近似，弹性波以透射为主，所以在频域上以支承层与支承结构反射回波的低频显著频域为主。带离缝病害无砟轨道的弹性波频谱以高频显著频谱为主。

(2) SST通过在时频域上挤压连续小波变换，可有效提取离缝缺陷回波信号显著频率开始时间和持续时长，提高了弹性波回波信号的频率分辨率，降低了由于系统噪声等原因形成的结构状态辨识误差，提升了无砟轨道离缝缺陷识别精度。