灾害时空属性下高铁时序网络韧性分析

王秋玲，柯宇昊，高诣民，程 承，王宇杭，林吉祥

(1.长安大学 运输工程学院，陕西 西安 710064；2.陕西省交通运输厅，陕西 西安 710075；3.西安市交通信息中心，陕西 西安 710018)

中共中央、国务院发布的《交通强国建设纲要》和《国家综合立体交通网规划纲要》中均明确提出，要增强我国高铁系统韧性[1-2]。高铁运输极度依赖交通基础设施，灾害可能导致整个运输系统受到破坏并难以正常运行[3]，研究异质灾害下高铁时序网络的韧性有助于认清高铁运输系统运输客流的能力，对保障高铁的稳定运营具有重要意义[4]。

高铁复杂网络韧性涵盖网络在部分损毁情况下，剩余网络所具有的疏解客流的能力[5]。ALBERT和BARABASI研究了复杂网络的可靠性[6]。随着研究的逐步发展，各国学者将高铁系统与复杂网络相结合，从高铁网络的拓扑结构出发，研究某一节点、连边或超边的失效对整个网络韧性的影响[7]。对此，研究人员多采取移除网络中的部分拓扑结构的方式对网络进行破坏，具体攻击策略主要涉及随机攻击[8]、蓄意攻击[9]。近年来，各国学者在拓扑韧性的基础上考虑了交通系统的运营情况，通过客流数据对网络中的连边加权，进一步研究高铁网络的运行韧性[10]。为在一定程度上克服结构韧性的局限，研究人员通过减小路段通行能力[11]、增加线路客流量[12]、考虑乘客换乘时间[13]等方法，将静态网络结构与乘客出行需求、运营方供给能力等情况相结合，但却较少考虑通过高铁时序网络来分析。此外，研究人员对自然灾害进行了大量的研究，研究主要集中于致灾因子及承载体属性[14]、自然灾害及灾害链时空属性[15]、应急救灾及灾后重建[16]等方面。侧重于探讨灾害对单个承灾体的影响[14]，而对整个系统的影响讨论较少[15-16]，尚未考虑到高铁网络面对灾害时空属性上的差异[6-8]，网络的连续删除策略往往没有考虑到攻击方式的时空异质性[10]；现有对于网络韧性的研究中，较少涉及灾害不同时段网络系统韧性的差异，并且多灾害下高铁网络韧性评估模型的分析较少[17]。针对上述问题，文中结合高铁运行时空特性构建高铁时序网络模型，提出一种考虑灾害时空异质性的节点删除策略，采用客观赋权法[18]对不同灾害进行权重测算，构建综合评估高铁时序网络韧性的模型，采用基于平均最短时序路径的网络韧性评价指标，分析高铁时序网络的韧性。文中将从常态和灾害态势下的高铁时序网络韧性、数据验证与实证分析，逐层深入展开。

1 常态下高铁时序网络韧性

本部分将分别从高铁时序网络构建与高铁时序网络韧性评价两方面来说明。

1.1 高铁时序网络构建

在现有研究的基础上[17]，考虑灾害往往会影响多个站点[19]，通过超边连接位于同一行政区域的节点，基于国内铁路列车时刻表构建高铁时序网络。网络节点代表不同高铁场站，网络节点之间存在的连边代表这两个站点在具体的时间段内存在列车的通行；根据行政区域的划分，将位于同一城市的节点采用超边连接。

高铁时序网络表示为Q=(G，E)，G={Gα|α∈(1，2，…，n)}是列车运行事件的集合，n代表列车运行的总事件数目，Gα=(i，j，t，Δt，g)表示的是列车运行的第α个事件，α代表列车运行事件的编号，i代表出发的节点，j代表到达的节点，t代表出发的时间，Δt代表出发持续的时间，g代表列车的编号。E={Eβ|β∈(1，2，…，m)}是列车时序网络中的超边集合，β代表城市超边的编号，m代表高铁时序网络中超边总数目。[T(u)，T(u+1)]是高铁时序网络中的时间窗口u，高铁时序网络示意图如图1所示，图中相同形状的节点位于同一超边，不同超边发生灾害的概率并不相同；层间连边的区别代表事件的异质性，层间连边代表不同行驶的列车运行事件，不同的列车采用不同形状的线条表示；底层的颜色代表网络层数的时序特性，网络层底层颜色越淡，代表时间越早。

1.2 高铁时序网络韧性测度

采用网络效率相对值这一常用[20]指标来衡量高铁时序网络韧性，网络效率相对值φ计算公式为

(1)

(2)

其中，N代表节点数目，duij代表时间窗口u内，节点i与节点j间的最短时序距离。φ的值越小，表示受灾后高铁时序网络中平均时序路径越长，高铁时序网络韧性越弱。其中两节点间的时序路径duij的公式为

(3)

其中，T(u)为时间窗口u的初始观测时间，T(u+1)为时间窗口u的结束观测时间，(t1ij，t2ij，…，tnij)代表从i点到j点第1次至第n次列车运行的开始时间，(Δt1ij，Δt2ij，…，Δtnij)代表从i点到j点第1次至第n次列车运行的持续时间。

2 灾害态势下的高铁时序网络韧性

灾害种类众多，基于分析的时间和效率考量，选择了较为常见的暴雨与地震[21]为代表进行阐述。下面分别对暴雨与地震下的高铁时序网络受灾概率进行分析，并通过熵权法对灾害赋权，在多种灾害并存的情形下，评估高铁时序网络的韧性。灾害对于高铁网络的影响方式包括攻击节点与攻击连边，考虑到这两类攻击的分析较为类似，为避免赘述，以攻击高铁网络节点为例，分析高铁网络面对灾害下的网络韧性。基于灾害的时空属性评估高铁系统的韧性，包括时间属性与空间属性[22]，因此在计算网络节点受灾概率时，需要分别计算时间维度与空间维度上节点受灾概率，即在特定灾害下每一时间窗口内的节点受灾概率以及每一省份的节点受灾概率。

2.1 暴雨下网络节点受灾概率

为保证预测精度，使用近10年的数据预测当前年度各省份发生暴雨频数，以及各时间窗口发生暴雨的频数，进而计算各省份发生暴雨的概率。本部分采用常用的三指数平滑算法[23]对暴雨时序数据进行预测，算法预测未来T期的值xt+T公式为

xt+T=AT+BT+CTT2，

(4)

其中，AT、BT及CT的计算公式为

(5)

(6)

为取得最优平滑系数，采用均方差计算误差：

(7)

当σ最小时，取得最优的平滑系数，(x1，x2，…，xt)是时间长度为t的历史数据。

将暴雨初始发生的时间按小时收集，暴雨发生时间段的概率与当年该时间段暴雨预测发生数量成正比，即时间窗口u发生暴雨的概率为

Pu1=Xu1/Xa1，

(8)

将暴雨发生的范围按行政区域划分，省级行政区发生暴雨的概率与当年该地区预测暴雨发生数量成正比，即省级行政区β发生暴雨的概率为

Pβ1=Mβ1/Ma1，

(9)

尽管暴雨及其引发的次生灾害会对高铁系统造成严重影响[24]，但由于高铁站点会倾向于建在更安全的地方，文中考虑的是暴雨不会直接损毁站点建筑但在暴雨发生时间内高铁场站的运行受到影响的情形。

2.2 地震下网络节点受灾概率

与暴雨场景不同，当地震对高铁造成影响，高铁场站存在完好与损坏两种情形。场站完好时，高铁列车暂时被扣下，在地震发生的观察时间窗口内，高铁列车的运行会受到影响；场站损坏时，高铁场站需要经过长时间的维修，一天的时间窗口内，高铁列车的运行都会受到影响[25]。地震发生的地点为省级行政区β，当高铁场站完好，在时间窗口u内，经过β内场站的列车停运；当高铁场站损坏时，所有的时间窗口内，经过β内场站的列车停运。

具体地，将地震初始发生的时间按小时收集，K={K1，K2，…，K24}代表24 h中每小时内我国发生地震的数量的集合，地震发生时间段的概率与历史发生数量成正比，即时间窗口u发生地震的概率为

Pu2=Ku2/Ka2，

(10)

将地震发生的范围按行政区域划分，Z={Z1，Z2，…，Zm}代表m个省级行政区内发生地震数量的集合，省级行政区发生地震的概率与该区域地震历史发生数量成正比，即省级行政区β发生地震的概率为

Pβ2=Zβ2/Za2，

(11)

2.3 考虑灾害时空属性的高铁时序网络韧性评价

2.3.1 高铁时序网络韧性多灾害权重算法

基于以往仅考虑单个灾害的时空属性的研究，在考虑灾害属性时讨论多个灾害同时存在时高铁时序网络韧性的变化，采用熵权法这一普遍采用的客观赋权法[17]计算不同灾害的权重。

将评价矩阵进行标准化处理后得到矩阵R={rxy|x=1，2，…，L；y=1，2，…，N}，其中

(12)

计算每个灾害的熵值为

(13)

最后计算每个灾害的熵权为

(14)

综合各种灾害的熵权，得到高铁时序网络韧性大小

(15)

其中，φx代表第x个时间窗口下，考虑多灾害时高铁网络的韧性。

2.3.2 高铁时序网络韧性多灾害评价算法

现有的高铁网络韧性评价模型较少考虑到灾害存在时间上的异质性，难以有效分析高铁在不同时间窗口韧性变化。基于以往研究，考虑了灾害发生与结束的时间，算法流程如下：依据列车时刻表数据建网，采用暴雨与地震灾害数据对网络进行攻击，测算损害前后高铁时序网络的网络效率相对大小，用以分析高铁系统的韧性，具体算法流程如图2所示。

3 数据验证与分析

3.1 数据来源与处理

3.1.1 铁路列车时刻表

基于铁路列车经过的高铁站点数据，确定当天高铁列车经过的站点分布于27个省级行政区域，列车时刻表数据来源于12306网站，包含48 000多条高铁运行数据，其示例如表1所示，到站时间为空值代表该站点为始发站，发车时间为空值代表该站点为终点站。

表1 铁路列车时刻表

3.1.2 高铁站点对应的超边数据

基于高铁站点的位置信息与省级行政区域划分数据，获得高铁站点与省级行政区域间的对应关系，其示例见表2。

表2 超边对应关系

3.1.3 暴雨灾害数据

基于中国降雨强度等级划分标准[21]进行暴雨强度划分，基于官方公示数据，收集从2011年1月1日至2021年1月1日各地级市日降雨量，示例如表3所示。除频率数据外，暴雨发生持续时间数据来源于文献[26]。

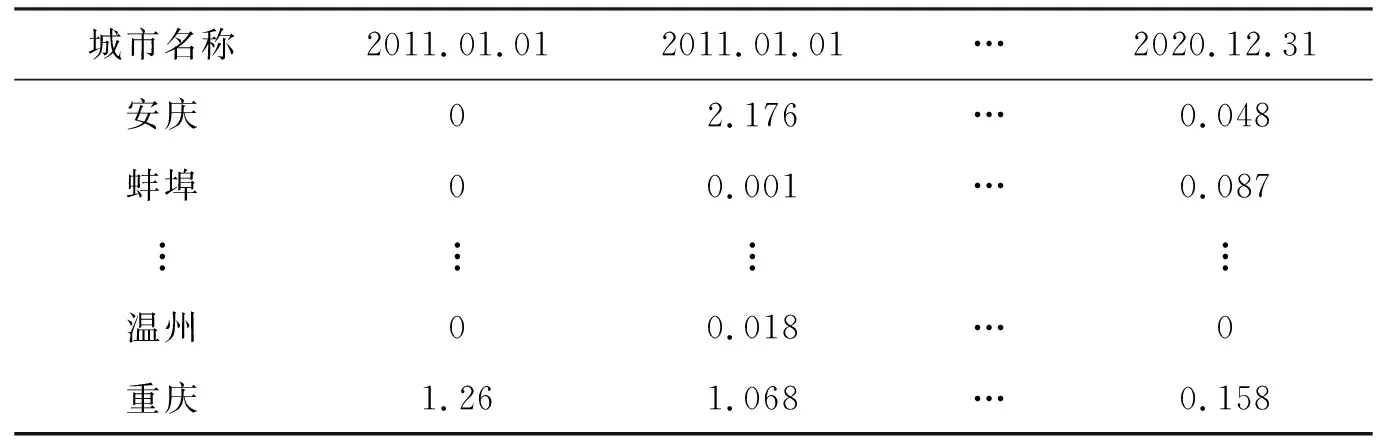
表3 各地级市降雨数据 mm

3.1.4 地震灾害数据

笔者选取对高铁运行造成明显影响4.5级以上的地震灾害数据[21]，特别地，按照铁路局地震应急预案中Ⅲ(较大地震灾害)应急响应的规定，当高铁场站遭受6.0级以上的地震时，将高铁场站视为损坏，以此计算高铁站点在地震下损坏的概率。地震数据的选取来源于中国地震台网中心，国家地震科学数据中心(http：//data.earthquake.cn)，地震数据从2011年1月1日至2021年1月1日，其示例如表4。

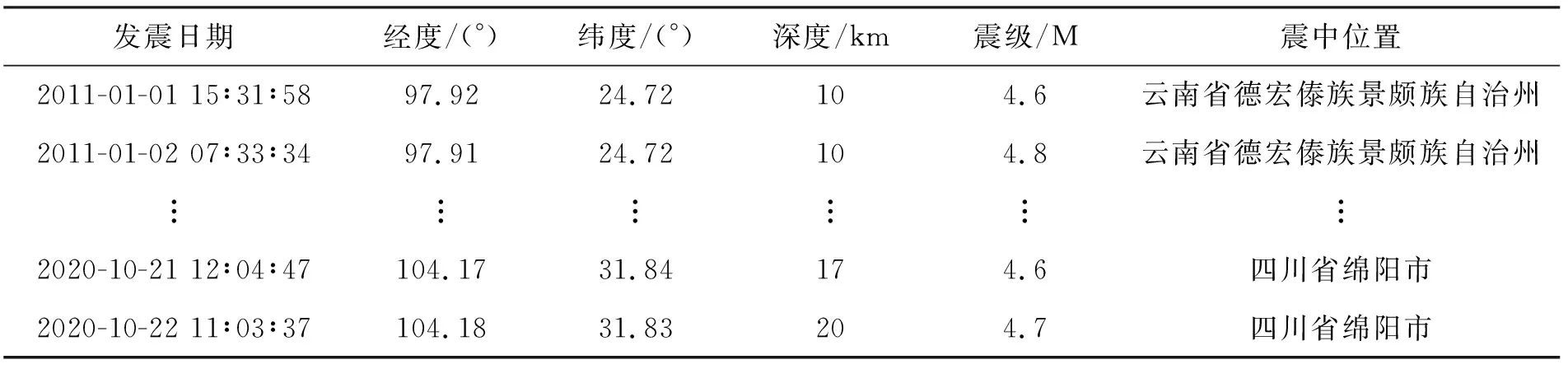
表4 地震数据

3.2 灾害数据分析

3.2.1 灾害区域数据分析

根据收集到的暴雨灾害数据与地震灾害数据，处理后得到各省级行政区的灾害发生概率如图3(a)所示。从图3(a)中可以看出，各省级行政区之间地震发生概率比暴雨发生概率差异性更大；内蒙古、天津及重庆的暴雨发生概率较低，分别为0.05%、0.02%及0.06%；北京、河南、湖南等7个省级行政区在选取的时间范围内没有4.5级及以上地震发生，地震发生概率低于其他省级行政区，而四川与云南为地震较频发地区，发生的概率分别为33.94%与31.67%。

从图3(b)中可知，在3 h后，随着暴雨持续时间的增加，暴雨发生的概率整体呈下降趋势。

将地震灾害数据按照发生时间所处的时间窗口进行统计，得到地震在不同时间窗口下的发生概率，如 图3(c)所示。

3.2.2 灾害时间数据分析

根据收集到的暴雨持续时间数据，按持续时长进行统计，暴雨持续时间概率如图3所示。分析一天内的高铁时序网络韧性，将暴雨持续时间对24取余，将超过一天的暴雨持续时间处理到1天内。

地震灾害的持续时间与震级相关，基于收集到的地震灾害数据，过去10年27个省级行政区，4.5级以上的地震共230次，6.0级以上地震共9次，经计算得出地震影响时间为24 h的概率为3.91%，地震影响时间为2 h的概率是96.09%。

3.3 韧性分析与结论

3.3.1 单灾害下高铁时序网络韧性

在单灾害下考虑节点发生灾害的概率[27]、时间窗口发生灾害的概率[28]及灾害持续时间的概率[29]进行高铁时序网络韧性研究，得到暴雨与地震后不同时间窗口下的高铁时序网络效率相对大小，如图4所示。

对图4中暴雨灾害进行分析，在14～16点网络效率相对大小最小为0.983，表明暴雨灾害在14～16点这一时间窗口，对高铁网络的损坏最大；由于高铁客运很少在夜间行车[30]，因此这两个时间窗口内，随机性的灾害较难影响高铁的运行，与图4中2～4点、4～6点时网络效率相对大小为1的情况吻合；不考虑0～6点时，6～8点高铁时序网络的网络效率相对大小最大，表明暴雨影响下6～8点高铁网络维持原有运营能力更强。

对图4中地震灾害进行分析，在6～8点时网络效率相对大小最小，为0.996，表明地震灾害在6～8点这一时间窗口，对高铁的损坏最大；在2～4点及4～6点时网络效率相对大小为1，其由于高铁客运夜间很少行车，随机性的灾害较难影响高铁的运行。不考虑0～6点时，22～24点高铁时序网络效率相对大小最大，表明在地震影响下，22～24点高铁网络维持原有运营能力更强。

对比分析暴雨与地震对于高铁时序网络韧性的影响，暴雨对高铁网络的损坏整体强于地震的损坏强度，这是由于分析灾害对于高铁系统韧性影响时，大多数的地震震级较低[31]，对高铁运行的影响时间较短。并且在不考虑0～6点这段高铁少有运行的时间段时，在14～16点这一时间窗口，暴雨影响下高铁时序韧性最弱，此时地震影响下高铁时序韧性较强。这一结果表明：灾害异质性使得在同一时间窗口内评估高铁网络韧性相差甚大。

3.3.2 多灾害下高铁时序网络韧性对比分析

将不同时间窗口视为“个体”，暴雨与地震下高铁时序网络的网络效率相对大小视为“评价指标”，采用权值计算公式(12)～(15)，测得暴雨与地震的权重分别为0.566 8与0.433 2。

为验证该算法的准确性，选取传统网络韧性评估模型以及最新文献[17]中的韧性评估模型，与文中模型进行对比分析，其结果如图5所示。

从图5中可知，多灾害条件下，高铁网络在14～16时网络效率相对大小最小，这表明在地震和暴雨灾害并存时，14～16点这一时间窗口内灾害对高铁网络的破坏性较大；而在2～4点及4～6点时，高铁网络的相对效率为1，这表明在这两段时间窗口内高铁网络较少受到灾害的影响，依然能够维持自身的稳定。

现有的对静态网络韧性分析的方法已较为成熟，即传统韧性分析方法[9]，因此计算文中模型以及文献[17]模型与传统网络模型的皮尔逊相关系数；当采用模型分析的结果与静态网络传统模型的相关性更强时，时序网络韧性分析模型更具有优越性[4]。模型间的皮尔逊相关系数ρ的计算公式为

(16)

通过计算，采用ρ1代表传统网络韧性评估模型结果与文中韧性评估模型结果的皮尔逊相关系数，采用ρ2代表传统网络韧性分析模型结果与文献[17]中韧性评估模型结果的皮尔逊相关系数。计算得ρ1为5.005 2×10-14，ρ2=5.658 9×10-15，从实验结果可以看出，笔者提出模型的皮尔逊相关系数高于文献[17]模型，具有一定的优越性。

采用传统网络模型测得高铁网络韧性为0.997 5，取值包含于文中模型测得的韧性区间，并且传统的网络模型无法表征出各个时间窗口下的高铁网络韧性的不同，而本模型可以表征出不同时间窗口高铁网络韧性的不同。在现有研究的基础上，笔者进一步考虑灾害的时空属性，使得文献[17]中模型的韧性明显弱于笔者提出模型的韧性，表明高铁时序网络的韧性整体是强于文献[17]中模型所表现出的韧性的。

现有高铁网络韧性研究中，并未区分灾害的异质性，而地震发生频次又远低于暴雨发生频次，因此，传统的网络分析模型中，弱化了地震对于高铁韧性的影响。采用熵权法对灾害进行权重计算，能够更为合理地评估地震与暴雨对高铁运行的影响。笔者研究得出不同时间窗口下高铁系统韧性会发生变化，因此高铁系统有关部门可根据相关研究，在不同的时间窗口内合理地分配防护资源，更有效地增强高铁系统的抗灾能力。

4 结束语

针对现有研究常将灾害视为简单随机攻击，忽略了灾害的时间特征与异质性，进而无法较全面分析高铁时序网络韧性的问题，笔者提出了一种考虑灾害时空时序下高铁时序网络韧性分析方法。该方法基于灾害开始时间、持续时间及空间地点的不同，提出单灾害下评估高铁时序网络韧性的模型；在此基础上通过熵权法计算不同灾害重要度，构建多灾害条件下高铁时序网络韧性分析框架。分析结果表明：笔者提出的模型可用于分析单灾害下高铁时序网络韧性，也能扩展到考虑更多灾害情形下的高铁韧性分析。后续可进一步探索不同攻击方式对高铁时序网络的影响。