判别与结构信息保持的无监督领域自适应方法

陶 洋，杨 娜，郭 坦

(重庆邮电大学 通信与信息工程学院，重庆 400065)

传统机器学习方法能够表现出高性能的前提是基于以下两个假设：(1) 大量且充分标记的样本保证模型能够得到充分有效的训练；(2) 训练数据和测试数据遵循独立同分布[1-2]。但是，在实际应用中，这两个假设很难成立。首先，有标记的样本是十分稀缺的，因为收集大量带有标签的训练数据需要投入大量的人力物力[3]；其次，难以保证训练样本始终具有与测试样本相同的分布。例如，不同分辨率以及不同外部环境下采集的图像数据具有不同的分布规律[4]。忽视数据分布差异而训练的机器学习模型，将难以取得良好的性能。

无监督的领域自适应方法能够利用具有完全标记信息的源域数据以及分布不同但语义相关的未标记目标域数据学习和构建跨领域学习模型，提高目标域数据的分类精度，可缓解互联网时代背景下数据量庞大，但标记数据不足的矛盾。尽管两个域的分布不同，但是存在一些潜在的共享信息。因此，如何发掘、提取和充分利用这些潜在共享信息，以降低两个域之间的数据分布偏差，提高跨领域学习效率，是领域自适应中的主要问题[5]。领域自适应方法可分为基于分类器的方法、基于特征表示的方法和基于实例的方法[6]。基于分类器的方法通常调整模型参数，将分类器适应于不同分布的数据来减少域偏差问题。基于实例的方法根据源域样本的重要性，通过样本重加权或选择源域样本来减轻分布的差异。而基于特征表示的方法强调学习在目标域和源域间学习一个公共子空间，通常可以取得较好的性能[7]。笔者主要对基于特征表示的方法进行研究，在现有的基于特征表示自适应方法中主要存在两个问题：(1) 通过特征变换的方式减少源域和目标域的差异，但是变换后的不同类别的样本缺少足够的判别性。(2) 在特征变换中丢失了数据的几何结构信息，导致过拟合问题，致使分类器难以取得理想的性能。

针对上述问题，笔者提出了一种新型的无监督领域自适应方法，在减少跨域分布差异的同时，最大化地保留了数据的判别信息和结构信息。具体地，利用目标域和源域数据之间的线性组合关系，联合学习一个潜在的不变子空间，有效减少跨域数据的分布差异。此外，通过非负松弛标签学习策略提高子空间投影的判别性，并使用源域类间稀疏补偿被松弛标签矩阵扩大的类内距离。与此同时，利用自适应概率图在判别的子空间中建立近似数据的连通性图结构，最大化地利用数据间的局部结构信息来增强子空间学习的鉴别力和鲁棒性。所提出模型的学习效果示意图如图1所示。其中，正方形、三角形和五角星形分别表示3种不同类别的样本，空心形状表示源域的样本，实心形状表示目标域的样本。P表示将两个域变换到子空间的转换矩阵，ICS(Inter-Class Sparsity)表示源域的类间稀疏约束，GR(no Graph Regularization)表示图正则化约束。

综上所述，文章的创新点总结如下：(1) 基于低秩约束构建数据跨领域重建模型，在此基础上通过标签松弛矩阵扩大来自不同类别样本的距离，并且使用类间稀疏约束缩小了同类样本的距离，同时保证源域数据的类内紧凑性和类间可分性，提高样本特征学习的判别性。(2) 在学习判别投影子空间的同时联合学习自适应概率图，使用自调整的技术来自适应地学习一个更加可靠的相似性度量，有效地保留数据的几何结构，提高目标分类器的性能，获得更高的分类精度。(3) 针对构建的无监督领域自适应模型，设计了一种基于交替优化的算法，以解决该模型的优化问题。在3个基准跨域数据集上进行实验，结果验证了该方法的有效性。

1 相关工作

1.1 子空间学习

子空间学习方法被广泛应用于计算机视觉、机器学习和模式识别等领域中[8]。子空间学习的中心思想是学习一个将原始冗余高维数据投影至低维空间的转换矩阵，在转换过程中，最大程度地保留数据的有效信息。随着对领域自适应的广泛研究，许多研究人员将子空间学习的思想应用于领域自适应方法中。受低秩表示的启发，文献[9]和文献[10]提出使用低秩重构的方法来减少跨域分布差异，通过将源域和目标域中的数据变换到一个公共子空间内，使得源域和目标域的分布近似相同。因为域间的数据重构能够有效地反映数据的内在信息，因此假设目标数据由公共子空间中的源域数据线性表示，并且通过对重建矩阵施加低秩约束，使得每个目标数据都可以由其在源域中的相似邻居来重建。子空间学习项的模型定义如下：

(1)

其中，P∈Rm×d，表示两个域之间的转换矩阵；XS∈Rm×ns，表示源域数据；XT∈Rm×nt，表示目标域数据；Z为重构矩阵。m是原始数据空间的维度，d表示该公共子空间的维度，ns是源域中的样本数量，nt是目标域中的样本数量。rank(·)表示一个矩阵的秩运算符，然而，秩函数的非凸性使得式(1)很难优化。因此，一般利用核范数作为矩阵秩的凸近似，等式可以被重新表述为

(2)

其中，‖·‖*表示矩阵的核范数。

1.2 图嵌入理论

在高维数据转到低维迁移子空间时，假设样本xi和xj在原始空间中是近邻关系，那么在子空间中也应该保持这种近邻关系；在流形学习中，这种保持近邻关系被称为局部不变性假设[11]。图嵌入作为模型的正则项，使得同类训练样本转化到标签空间后能够紧密地聚集在一起。因此在领域自适应方法的模型中增加图结构约束，对整个模型的学习都十分有利。图嵌入的目标函数如下：

(3)

其中，P为变换矩阵，W为权重矩阵，n表示样本数量。

2 方法描述

领域自适应的目的是为了充分利用源域数据知识，学习一个对目标域有效的分类器。虽然通过基于低秩重构的子空间学习模型能够学习源域和目标域之间的公共子空间，以减少数据的分布偏差，但是却丧失了数据的判别能力，导致分类精度不理想。因此在特征学习过程中，减少域偏移的同时还必须保持原始特征中蕴含的一些有效信息，例如判别信息和结构信息。

2.1 保留源域的判别信息

为了提高模型的性能，应该充分考虑不同类中源域数据的结构差异，在公共子空间中保留源域的判别信息，最大化源域不同类样本的类间距离。传统的线性回归方法假设训练样本可以精确地转换为严格的二值标签矩阵YS，通过在二值标签矩阵中引入一个非负标签松弛矩阵M，将严格的二值标签矩阵放松为松弛变量矩阵YS+B⊙M。受文献[12]的启发，考虑到l2，1具有行一致性稀疏的特性，利用l2，1范数损失函数提高对噪声干扰信息度量的鲁棒性。判别子空间学习函数的定义如下：

(4)

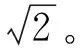
(5)

式(5)的第1项放松标签矩阵旨在扩大不同类别之间回归响应的距离，第2项通过保持同类样本的行稀疏一致性，可以降低同类别样本在投影后的距离。

2.2 保留数据的几何结构

在源域向目标域知识迁移过程中，引入图结构来保持局部临近信息。更重要的是，如果过于强调源域的判别信息而忽略数据内部的非线性几何结构，得到的子空间会很容易在源域样本上产生过拟合，图嵌入能够有效解决该问题。已有的图结构学习方法通常在原始高维空间中基于距离相似性建立数据的连通性，但是高维空间的冗余信息和噪声会使得这种连通性不可靠。因此，笔者在判别的子空间中建立了图结构，基于概率连通性为每个数据点自适应地分配最优邻居，假设在判别子空间中密切相关的样本具有更高的连接可能性。通过以下图正则项来定义：

(6)

其中，ddist(a，b)表示样本a和样本b之间的距离，en表示n维全1向量，约束矩阵Q是转移概率矩阵，其每一个行都是一个概率分布。使用欧氏距离的平方定义任意两个在子空间中数据的距离。为了避免转移概率矩阵Q出现平凡解，将式(6)可以重写为下式：

(7)

2.3 判别与结构信息保持的无监督领域自适应方法模型

将子空间学习项(2)、判别子空间学习函数(5)、图正则项(7)结合，得到最终的目标函数：

(8)

其中，λ和β是权重参数。第1项和第2项共同构成判别子空间学习项，可以扩大来自不同类的两个数据点之间的距离，并缩小来自相同类的两个数据点之间的距离，提高共享空间内目标域和源域特征表达的准确性，从而减少源数据和目标数据的分类误差。第3项是一个低秩约束，它能够强化重构矩阵Z的分块结构特性，保证每个目标域样本能够由其源域中的近邻表示。第4项是一个图正则化项，从样本的角度保留了数据的空间关系，同时避免了过拟合。

3 模型优化

3.1 模型优化

针对构建的领域自适应模型式(8)，将详细描述目标函数的优化求解方案。考虑到模型式(8)是一个非凸问题，因此通过固定其他变量迭代更新每个变量。

首先，引入3个辅助变量E，Z1和F，以及相对应的两个等式约束。式(8)可转化为如下优化问题：

(9)

式(9)可以通过非精确增广拉格朗日乘子法(IALM)进行优化[16]，进一步转化为

(10)

其中，C1，C2，C3，C4是拉格朗日乘子，μ≻0是惩罚因子。等式中的变量不能同时进行优化，引入交替优化的策略。

更新P：通过固定其他变量，得到P的子问题，并将其重写为基于图的紧凑形式：

(11)

类似地，通过删除其他不相关的变量，可以求得Z和Z1的解。

更新E：固定其他变量，通过以下子问题求解E：

(12)

(13)

更新M：固定其他变量，根据文献[9]，通过以下方法求解M：

(14)

更新F：与求解E相似，删除其他无关变量并将其转化为独立的子问题可以求出F的解。

更新Q：固定其他变量，能够得到关于Q的子问题。将其继续分解为n个独立的子问题，并且每一个子问题都有相同的形式。根据文献[14]，得到Q的子问题qi的最优解和σ的值：

(15)

3.2 计算复杂度分析

4 实验结果与分析

为了验证所提出方法的有效性，使用3个广泛使用的跨域图像数据集开展实验验证工作，3个数据集分别为：① 4DA目标数据集，由Office数据和Caltech-256数据构成。共有A(Amazon)、C(Caltech-256)、D(DSLR)和W(Webcam)四个域。在实验中，分别使用浅层SURF特征和深层DECAF6特征，通过交替部署成对域(源域和目标域)，共构建了24个跨域任务。② COIL20 3D对象数据集，包含20个对象，其中有1440张灰度图像(每个对象有72张多姿态图像)。该数据集分为两个子集COIL1(C1)和COIL2(C2)，在构建源域和目标数据时考虑两种设置：C1→C2和C2→C1。③ MV数据集，由MSRC和VOC2007两个数据集构成。实验使用这两个数据集共享的6个的语义类别，分别为飞机、鸟、羊、牛、自行车和汽车。建立了两个任务：M→V和V→M。实验所用数据集图像示例如图2所示。

实验所使用的对比算法，包括两种未进行领域自适应的方法NN分类器和AlexNet[15]，7种传统领域自适应方法：GFK[16]、LTSL[17]、JDA[18]、LRSR[9]、BDA[19]、LRDRM[20]和SPDA[21]，以及两种深度领域自适应方法：DDC[22]、DAN[23]。考虑到方法对比的公平性，采取了与其他方法的相同的评估指标和实验设置，实验结果见表1～4，其中分类精确度最高值通过加粗表示。

表1 COIL 20数据集上的精度 %

表2 MV数据集上的精度 %

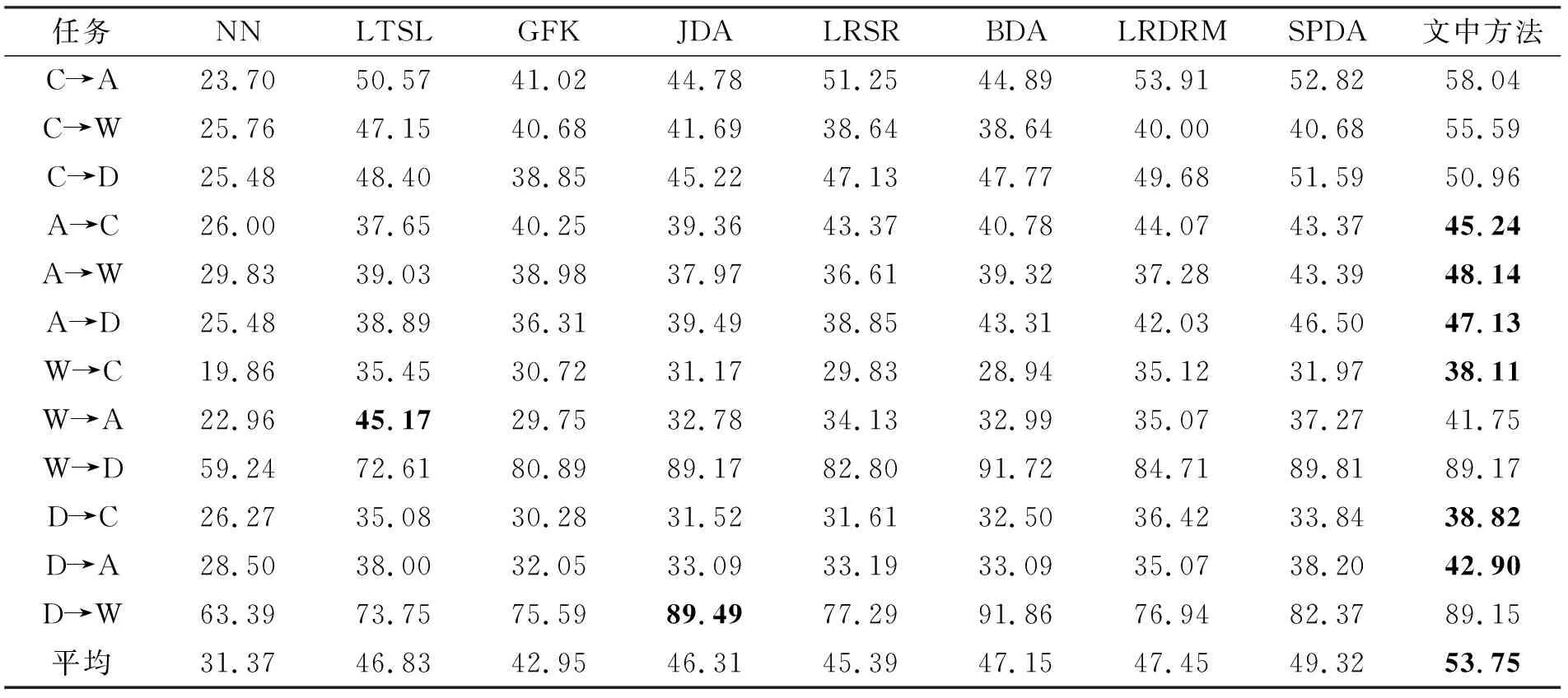
表3 4DA(SURF)数据集上的精度 %

4.1 实验结果分析

COIL20数据集的实验结果见表1。从表可以看出，笔者提出的方法平均性能优于大多数其他比较方法的性能。与基线方法相比，NN分类器没有进行领域自适应，性能比提出的方法低15.07%左右。这表明笔者提出的方法完成了源域到目标域的知识迁移。SPDA方法取得了最优的分类性能，这可能是因为该方法不仅保持了几何结构信息，而且同时减少了条件分布和边缘分布差异。

MSRC-VOC2007数据集的实验结果见表2。结果表明，与最新的领域自适应方法LRDRM相比，当VOC2007数据集是源域时，MSRC数据集是目标域时，分类精度提高了3%。尽管当MSRC数据集是源域时，VOC2007数据集是目标域时，笔者提出的方法分类精度没有取得最优的结果，但是与其他类似的方法相比，提出的方法获得了最高的平均分类精度。

4DA数据集的实验结果见表3和表4。表3为具有SURF特征的4DA数据集实验结果，在12个跨域任务中，提出的方法在8个任务中获得了最优的性能，并且取得了更好的平均性能。LTSL、LRSR和SPDA与所提出的方法都属于迁移子空间学习方法，但是LTSL没有进行源域的判别学习，LRSR虽然学习了源域的判别信息，但是忽略了保持类内的紧凑性和数据的几何结构，SPDA是在原始高维空间中保持的数据几何结构。笔者提出的方法较最优对比方法SPDA精度提高了约4.43%。表4为具有深度DECAF6特征的4DA数据集实验结果，其中带*号表示是深度领域自适应方法。DDC和DAN是两种深度学习领域自适应方法，由于深度神经网络的非线性和层次表示能力，使得这两种方法取得了比大多数非深度方法更优的结果。但是笔者提出的方法和SPDA的性能仍然优于DDC和DAN，原因可能在于DDC和DAN没有利用域自适应层中数据的结构信息，而SPDA和笔者的方法在减少分布差异的同时保留了数据的流形结构。

表4 4AD(DECAF6)数据集上的精度 %

4.2 消融分析

与现有的方法相比，笔者提出的方法引入了源域的类间稀疏约束和自适应图正则项。为了验证其有效性，进行了3个实验与笔者提出的方法作比较。使用4DA(DECAF6)数据集进行消融实验。

第1个实验是一个不包含自适应图正则项和源域类间稀疏约束项的简单模型，称为“原始”，该实验的目标函数如下：

(16)

第2个实验评估了自适应图正则化项对模型性能的影响，称为“No-GR”(No Graph Regularization)，表示不使用图正则化项约束。该实验的目标函数如下：

(17)

第3个实验评估了具有源域类间稀疏约束的判别子空间项是否提高了模型的性能，称为“No-ICS”(No Inter-Class Sparsity)，表示未进行源域的类间稀疏约束。目标函数如下：

(18)

不同模型的实验结果见表5。从表中可以看出笔者提出的方法性能最好，这表明源域类间稀疏提高了迁移子空间的判别性能，以及所提出的自适应图正则项在迁移过程中保留样本几何结构的有效性。

表5 4DA(DECAF6)数据集上消融实验结果 %

为了更好地直观地展示所提方法跨领域共享子空间的学习效果，对4DA(DECAF6)数据集中C→D跨域任务进行了t-SNE可视化，图3(a)展示了C→D任务的原始特征。图3(b)和(c)展示了式(15)和式(16)学习到的数据表征。图3(d)为笔者提出的方法学习到的数据表征。不同形状表示不同类别的数据，通过图示可以清楚地看到同一类别的数据分布相近，不同类别的数据互相远离。这表明了学习到的数据表征的强判别性。通过对比图(a)～(b)和图(d)，可以看出域间差异的不断减少。

4.3 参数敏感度分析

如式(8)所示，该目标函数有两个参数：保证数据类间稀疏性结构参数λ和图正则项β。为了分析该方法的参数敏感度，本节实验测试了λ和β两个参数不同值的组合下对算法性能的影响。参数λ和β的取值范围设置为{0.001，0.005，0.01，0.05，0.1，0.5，1，5，10}。具有不同参数的W→D(SURF)、A→D(DECAF6)、COIL2→COIL1的计算结果如图4所示。由图可知，虽然两个参数对所提出的模型在多个不同的数据集上性能变化有所不同，但是在比较大的参数区间范围内，可以取得稳定并令人满意的分类准确率。

4.4 算法运行时间对比

本节对比了提出的算法与GFK、JDA、LRSR、BDA和SPDA算法的运行时间。所有的测试都在一台CPU为Intel 1.8GHz双核处理器、内存为8GB的计算机上完成，软件平台选定为MATLAB R2016b。本节实验在4DA(SURF)数据集的C→A任务和COIL数据集的C1→C2任务上进行实验，各个算法的执行时间如表6所示。其中GFK算法的运行时间最短，但是该算法的分类精度相对而言较低。LRSR算法的运行时间最长，这是因为该算法的收敛速度相较于其他算法较慢。笔者提出的方法并不是时间成本最高的算法。

表6 算法运算时间对比

4.5 讨论

值得注意的是，所有的实验结果都显示领域自适应方法的性能优于标准的机器学习方法。这进一步验证了当训练数据和测试数据来自不同的领域时，导致分类性能差的原因主要是因为域间分布不同。如果能够尽可能地减少源域和目标域之间的分布差异，就能利用源域充分标记的样本来学习未标记的目标样本，使得使用源域内的标签信息成为了可能。但是在学习新的跨领域特征表示时，也应该考虑保持原始特征的判别能力，否则一味地减少分布差异，容易导致目标样本不可分，这对分类任务十分不利。并且也不能忽视数据的局部结构信息，否则会导致模型的泛化性能差，容易引起过拟合问题。这3点对于学习分类器都有良好的促进作用，能够得到更准确的目标分类器。笔者提出的方法将上述的3个目标融合为一个框架，在多个跨域数据集任务上的实验结果表明了该方法的强判别性、泛化性和有效性。本研究更注重于分类精度的提升，结合源域类间稀疏性约束与图正则项后的目标函数模型较为复杂，其分类精度的提升是牺牲了一定的时间复杂度换取的。

5 结束语

笔者提出了一种判别与结构信息保持的无监督领域自适应方法。在源域至目标域的知识迁移过程中，通过松弛标签矩阵和源域类间稀疏约束充分的保留了源域的判别性能，联合自适应图约束能够在保留样本的几何结构同时避免学习过拟合的问题。大量实验结果表明，在迁移过程中保留这些重要属性对模型分类性能提高的有效性。