基于伴随网络的受端电网多馈入短路比约束线性化建模
李少岩,曹 珂,顾雪平,任乙沛
(1. 华北电力大学电气与电子工程学院,河北省保定市 071003;2. 国网湖北省电力有限公司武汉供电公司,湖北省武汉市 430012)
0 引言
为缓解中国可再生能源与负荷中心逆向分布的矛盾,促进以“碳达峰、碳中和”为目标的能源转型,在远距离、大容量输电方面具备独特优势[1-2]的基于电网换相换流器的高压直流(line commutated converter based high voltage direct current,LCCHVDC)输电技术得以快速发展。随着多回直流馈入同一受端交流系统,为避免由于电压支撑不足导致的直流相继换相失败[3],受端电网必须具备足够坚强的网架结构以降低直流系统承受的潜在安全风险。
在电力系统规划建设和运行控制中,通常需要进行输电网拓扑结构的优化或决策,以实现系统经济性或其他性能指标的提升。文献[4]指出通过合理的线路扩展规划可以有效缓解电网的输电阻塞。文献[5]对输电网结构优化在降低系统发电成本、处理紧急故障等方面的应用研究进行了综述。文献[6]提出了一种在紧急情况下以电网分区的方式实现连锁故障阻断的有效策略。对多馈入系统而言,网架拓扑的变化很可能破坏系统强度,对多馈入短路比(multi-infeed short circuit ratio,MISCR)造成明显影响。因此,在相关问题的优化建模中必须有效计及MISCR 约束。作为衡量交直流电网结构品质的重要指标[7],近年来不断有学者开展关于MISCR的研究。CIGRE 工作组较早地给出了MISCR 的定义,为指导大规模交直流系统的规划及运行提供了重要依据[8]。文献[9]在此基础上进行了实用化推导,得到了该指标的简化计算方法。此后,学者们也对MISCR 在受端电网分区规划[10]、限流措施优化配置[11-12]、主动解列方案决策[13-14]中的应用进行了诸多探索。然而,在上述涉及交流网架拓扑调整的场景下,已有模型缺乏对MISCR 与决策变量之间显性关系的讨论,因而大多采用启发式算法进行求解,结果的最优性难以保证。
随着运筹学的发展及应用,近年来很多学者在解决电网优化问题时常采用数学规划方法,其优势在于只要将模型构建成混合整数线性规划等特定形式,即可通过成熟的商用优化求解器得到全局最优解[15]。目前,基于线性规划的输电网规划和运行控制优化模型已得到广泛应用。因此,亟须提出一种MISCR 约束的线性化建模方法用于保证受端电网的安全性。由于网架拓扑调整总是通过改变换流母线的自阻抗和互阻抗,进而对MISCR 产生影响,因此,节点阻抗元素的建模是其中的难点和关键。在前期的研究中,文献[16]已提出了节点阻抗线性自保持模型,但仍是以交流系统为研究对象,缺乏对MISCR 的直接讨论。
基于上述问题,本文以节点阻抗元素的物理意义为切入点,通过构建与原网架拓扑相似、支路开断状态随动的伴随网络,实现了MISCR 约束关于支路状态的线性化解析建模。然后,将提出的方法应用于受端电网主动解列和最优线路开断(optimal transmission switching,OTS)模型。最后,算例结果验证了本文所提约束的正确性和有效性。
1 MISCR 与节点阻抗元素之间的关系
1.1 MISCR 的定义
CIGRE 工作组综合考虑交流系统短路容量、多回直流输电容量以及各换流站间的电气耦合关系,给出了MISCR 的定义:
式中:Pdi和Pdj分别为第i、j回直流传输功率的标幺值;Zeq,ii为等值节点阻抗矩阵中第i回母线的自阻抗;Zeq,ij为换流母线之间的等值互阻抗。
由MISCR 与换流母线节点阻抗之间的关系可知,若在系统规划或运行中对受端电网的拓扑结构进行调整,则MISCR 既可能增大也可能减小。这种不确定性表明网架拓扑的变化会使系统承受潜在的安全运行风险。因此,在相关的优化模型中引入MISCR 约束是很有必要的。
1.2 节点阻抗元素的物理意义
由式(2)可知,MISCR 约束建模的关键在于节点阻抗元素的获取。在涉及网架拓扑调整的优化问题中,支路的投运状态并非预先给定,而是作为决策变量参与优化。因此,若想完成MISCR 的建模,首要前提是实现节点阻抗元素关于决策变量的线性化表达。
传统研究采用的节点导纳矩阵求逆法和追加支路法受限于阻抗矩阵生成过程的强非线性,无法适用于混合整数线性规划模型的构建与求解。文献[17]推导出节点阻抗矩阵与线路运行状态的线性函数关系,但其只是一个近似矩阵,含有误差,且仍存在由矩阵求逆导致的非线性问题。文献[18]利用节点导纳矩阵与节点阻抗矩阵之积为单位矩阵的特点,推导并建立了对节点阻抗矩阵的精确约束,虽回避了文献[17]中线性化带来的误差,但建模过程较为复杂。
基于上述不足,本文以节点阻抗元素的物理意义为切入点,进一步探索MISCR 与支路状态之间的线性化建模方法。节点电压方程可表示为:

式中:Zij为节点阻抗矩阵第i行第j列的元素,i,j=1,2,…,m;Ii为节点i的注入电流;Ui为节点i的电压值,当选择大地为参考节点时,Ui即为节点i的对地电压值;m为系统节点数。
观察式(4)可知,当向节点i注入单位电流源时,其他节点所接电流源均开路,即当Ii=1、Ij=0(∀j≠i)时,有Ui=Zii、Uj=Zij。由此可知,在仅含单位电流源注入的特定网络中,各节点阻抗元素可以由相应的节点电压值加以表征。
2 MISCR 约束的线性化解析建模
2.1 基于单源多网的MISCR 约束建模
本节结合一个三馈入的受端系统说明基于节点阻抗物理意义的MISCR 建模方法。假设该系统共包含2 台机组、8 个节点、10 条线路以及3 个LCCHVDC 系统,具体拓扑结构如图1 所示。
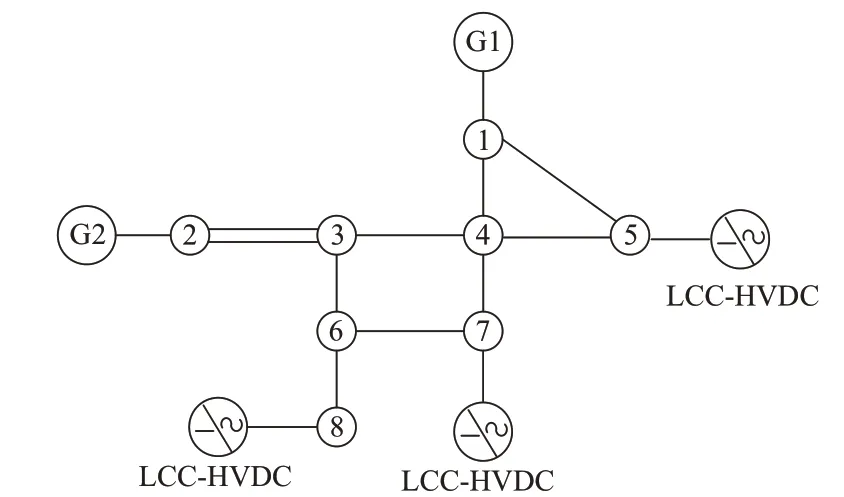
图1 多馈入系统示例图Fig.1 Example of multi-feed system
以节点8 为例具体说明。为实现该节点处的MISCR 约束建模,需要对节点8 的自阻抗及与另2回直流落点间的互阻抗进行提取。首先,构建一个与原网络拓扑结构相似但参数不同的纯电抗伴随网络:机组以暂态电抗的接地支路表示,变压器和线路统一采用电抗近似表示,并在目标节点8 处施加一个单位电流源I8,如图2 所示。其中:xGi为机组i的暂态电抗值;xijc为支路电抗,其中下标c为回路编号;电流源I8=1。在此伴随网络中,节点集合由N扩展为包含大地节点的N0,线路集合K扩展为包含接地支路的集合K0。
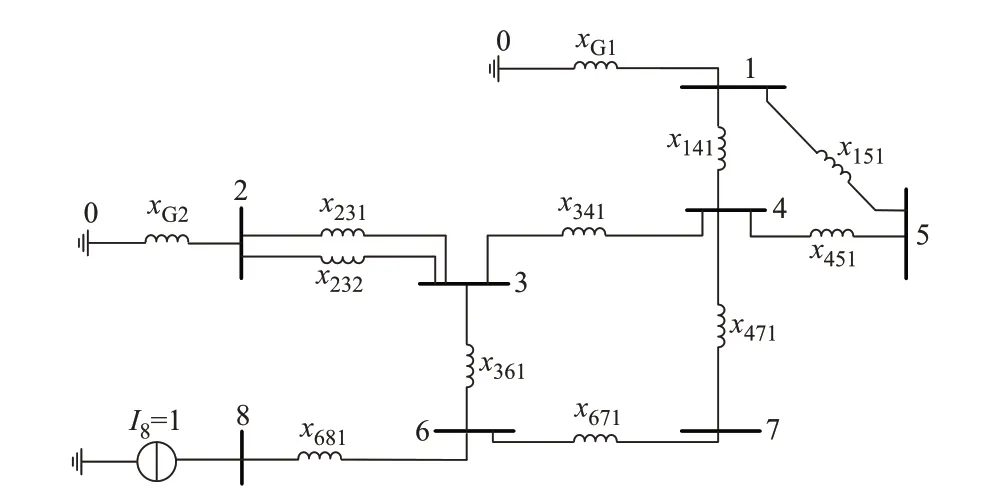
图2 提取MISCR 的伴随网络Fig.2 Accompaniment network for extracting MISCR
结合节点阻抗元素的物理意义可知,在针对节点8 构建的伴随网络中,该节点的电压值即为自阻抗值,节点5、7 的电压值即为各自与节点8 之间的互阻抗值。当构成MISCR 的目标阻抗元素均已知时,便可将节点8 的MISCR 下限约束转化为节点电压与直流功率线性组合的上限约束。具体建模如式(5)所示。
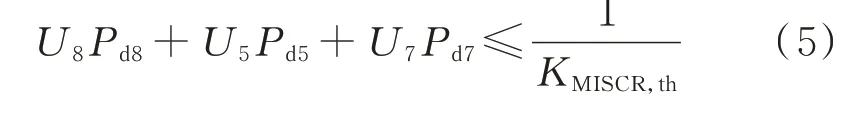
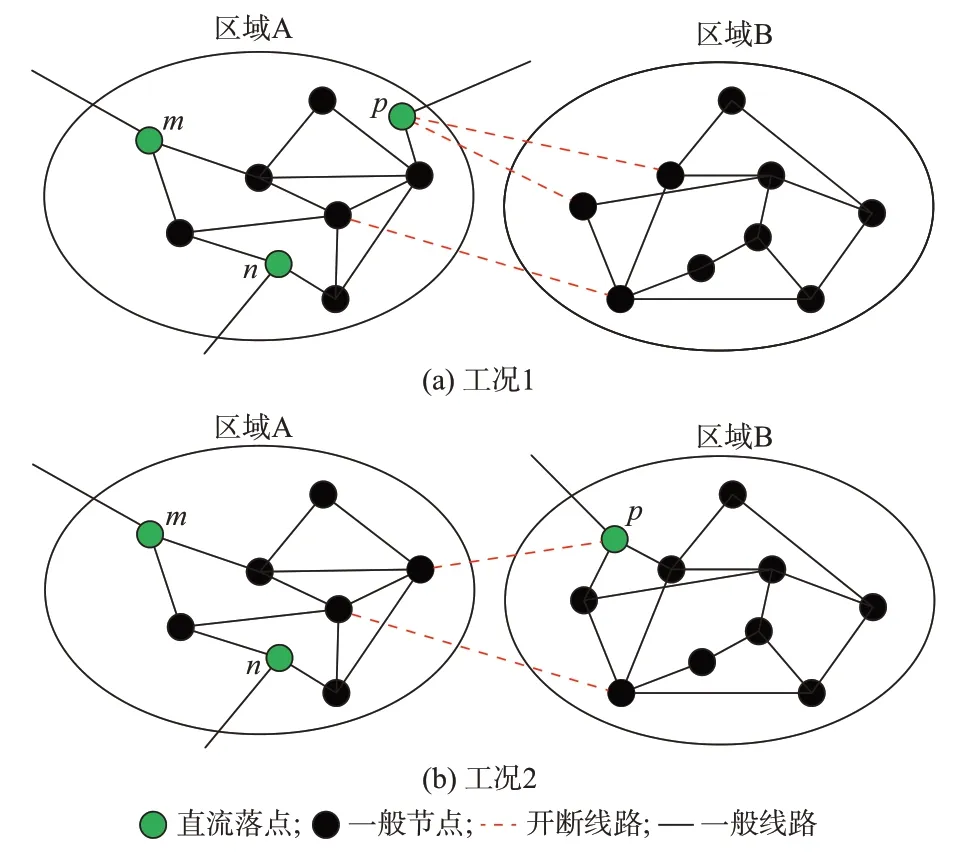
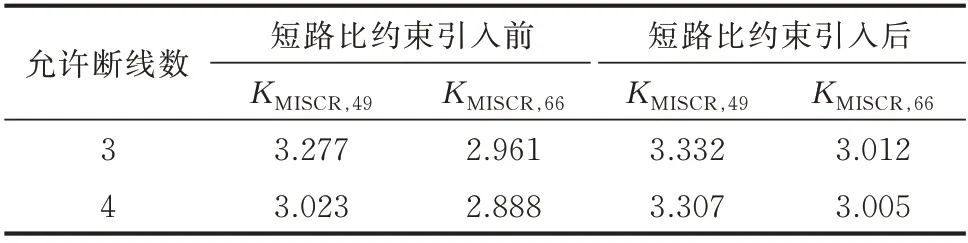
式中:KMISCR,th为设定的理想MISCR 阈值,通常取值为3。一般认为,KMISCR>3 时受端系统为强系统;2 依此类推,当电网中含有多回直流馈入时,需要针对每个直流落点构建一个相应的伴随网络,用于提取与MISCR 相关的各节点阻抗元素。由于上述方法需要根据馈入直流的数目构建多个伴随网络,且每个网都附加一个单位电流源,因此称之为单源多网模型。其中,为提取MISCR 约束所构建的伴随网络之间相互平行,共同辅助主网进行网架拓扑决策优化。其内在关系如图3 所示。 为了将MISCR 与支路状态之间的关系线性化,还需借助2 个基本的电路定律,即 式中:NHVDC为多馈入系统直流落点的集合;下标f表示基于直流落点f构建的伴随网络;Iijc为伴随网络中流过线路的电流;bi为伴随网络中注入节点的电流源大小;M为一个极大的数,用来松弛相关的不等式约束;Zijc为网架拓扑优化的决策变量,Zijc=0 表示支路被断开,Zijc=1 表示支路投入运行。 式(6)为基尔霍夫电流定律(KCL)约束式;式(7)保证各伴随网络中只有直流馈入点处有单位电流源注入;式(8)表示除大地节点和直流落点之外的节点都满足电流平衡;式(9)和式(10)为大M 法表达的线路欧姆定律;式(11)可以保证当Zijc=0 时线路无电流流过;式(12)为节点电压表征的MISCR约束。 单源多网模型通过构建一系列伴随网络,实现了MISCR 约束关于支路状态决策变量的线性化表达。需要注意的是,伴随网络中流过的电流与原电网中的潮流无关,它们是两种完全不同的网络流。由于两层网络在优化过程中使用同一组决策变量,原网络的拓扑变化可以实时映射在伴随网络中,两者可以保持很好的随动关系。因此,无论系统结构如何变化,伴随网络总能准确刻画MISCR 与支路状态之间的动态关系,从而更好地服务于网架拓扑决策优化。 在单源多网模型中,若要完成所有换流母线处的MISCR 建模,需要针对每个直流落点构建一个相应的伴随网络。那么,当直流落点数增多时,模型中的约束条件集合将会快速扩充,不利于求解。为此,本节提出了一种更加简洁高效的MISCR 约束建模方法。 假定传输功率为Pdi、Pdj、Pdk的三回直流分别落点于母线i、j、k,将式(4)中各直流落点的节点注入电流用相应的传输功率标幺值替代,其余节点电流均设为零,则节点电压方程可展开为: 由式(14)可知,当向直流落点处同时注入各自传输功率大小的电流源时,换流母线的节点电压值与其MISCR 互为倒数。因此,可以通过构建具有如下特征的伴随网络,实现MISCR 约束的线性化建模。 1)每个直流馈入点处外施一个电流源,其他节点不设置电流源。 2)外施电流源的大小与相应的直流传输功率标幺值相等。 3)换流母线处的节点电压值与相应的MISCR互为倒数。 本节仍以图1 所示三馈入系统为例,说明基于多源双网的MISCR 约束建模方法。首先,将机组、变压器、线路等效为纯电抗支路,按照上述3 个特征完成伴随网络的构建,如图4 所示。伴随网络与原网络之间的映射关系见附录A 图A1。 图4 基于多源双网模型的伴随网络Fig.4 Accompanying network based on multi-source dual-network model 在图4 所示的伴随网络中,根据MISCR 与节点电压之间的倒数关系,可将前者的下限约束转化为后者的上限约束: 式(15)为KCL 约束式;式(16)保证伴随网络中只有换流母线处有电流源注入;式(17)表示除大地节点和直流落点之外的节点满足电流平衡;式(18)和式(19)为欧姆定律;式(20)为线路容量约束;式(21)为用节点电压直接表征的MISCR 约束。 通过对比,该模型与单源多网模型的不同首先在于每个伴随网络中的单一电流源变成了多个电流源,可由式(16)体现;其次,MISCR 由一个节点电压与直流馈入功率的线性组合约束转化为直接对直流落点处的电压值通过式(21)加以限制。相比之下,多源双网模型对于伴随网络中节点电压的物理意义进行了更充分地挖掘和利用。此外,由单源多网到多源双网的推演可知,无论是单一节点阻抗元素,还是由多个节点阻抗元素线性加和形成的指标,都可以通过构建特定的伴随网络实现相应指标与支路状态之间映射的线性化建模。 本节中的伴随网络只是多源双网模型中的一张网,用来提取所有的MISCR 约束,另一张网将在3.2.2 节中进行介绍。 网架拓扑调整过程中,一系列的开断操作有时会使全网的连通性遭到破坏,导致多个直流落点分散在同一区域或不同区域中。此时,本文提出的MISCR 建模方法依然有效。为说明这一点,本节将对该方法在网架不连通工况下的适用性做进一步分析。假设由于网架拓扑调整导致含有三回直流馈入的受端网架被分成两部分,如图5 所示。 图5 2 种网架不连通工况Fig.5 Two kinds of unconnected grid operation conditions 在工况1 中,原网架被分割成2 个子系统:三回直流同时落点于区域A 中;区域B 为纯交流系统。在工况2 中,原网架被分成一个多馈入系统A 和一个单馈入系统B。 2.3.1 单源多网模型的适用性分析 工况1:当向区域A 中的某个直流落点注入单位电流源时,该节点的电压值为其自阻抗值,其余节点电压均为与该节点间的互阻抗值。由于区域B 与区域A 完全割裂,区域B 中没有电流源注入,因此,各节点电压始终为零,对MISCR 没有贡献。区域A中阻抗元素与节点电压之间的映射关系保持良好,物理意义明晰,直流落点的电压值可直接用于构建MISCR 的约束表达式。 工况2:当向区域A 中的m或n点注入单位电流源时,另一直流落点的电压即为两者间的互阻抗。p点所在的区域由于没有电流源注入,节点电压保持为零,即Zmp=Znp=0。于是区域A 中两节点的MISCR 退化为双馈入系统的短路比。同理,当向节点p注入电流源时,区域A 中各节点电压均为零,以电压值表示的节点p短路比退化为传统短路比。由于单馈入系统与多馈入系统通常所采用的系统强弱划分标准一致[19],因此,退化后的约束式仍可用于保证区域B 这个单馈入系统的网架结构强度。 2.3.2 多源双网模型的适用性分析 工况1:若向区域A 中的3 个直流馈入点同时注入直流功率大小的电流源,此时3 个节点电压值的倒数可以用来正确表征该多馈入系统的3 个短路比。不含直流落点的区域B 由于没有电流源注入,各节点电压均为零,对区域A 中各节点电压与MISCR 之间的映射关系没有影响。 工况2:当向3 个节点同时注入电流源时,区域A 中各节点的电压特性由节点m、n处发出的电流在网络中流动建立,因此只反映了这2 个直流落点之间的相互作用,与区域B 中的另一直流落点及其施加的电流源无关。而对区域B 而言,节点p的电压值与节点m、n处注入的电流源无关,只反映了所在单馈入系统的短路比特性。 综上,即使是在网络连通性被破坏的情形下,伴随网络中节点电压与阻抗元素或MISCR 之间依旧能够保持良好的映射关系。由此说明本文提出的节点阻抗建模方法并不受限于网架结构的连通状态,具有很大的灵活性。 为了避免极端情况下系统崩溃,主动解列作为电力系统第3 道安全防线的重要手段,通过将局部电网从主网中分离,最大限度地保证负荷分区不间断供电[20-21]。考虑到交直流受端电网解列后某些孤岛内可能存在直流的情况,在进行主动解列决策时应兼顾MISCR 约束以确保子系统内各直流的稳定运行。 式中:gd为解列后系统的分区编号;Zijc,gd为线路在分区gd中的投运状态;PHVDC,i为节点i处的直流馈入功率;Pg为发电机g的有功出力;Pijc为线路有功潮流;Pming和Pmaxg分别为发电机g的最小和最大出力;θij为两节点间的相角差;Pmaxijc为线路容许潮流的最大值;Gi为包含节点i所接的所有发电机的集合;G为所有发电机的集合。 式(23)为功率平衡方程;式(24)为发电机出力约束;式(25)和式(26)为直流潮流方程;式(27)确保线路潮流不越限;式(28)为相角差约束。 (2)同调群连通约束 在主动解列模型中,需要保证同调机组之间是相互连通的。首先,选择需要保证连通性的节点,共同构成集合Ns;然后,选择其中一个节点作为源点,其余节点均为汇点,构成集合N's。将解列后的每个子系统视为一个单源多汇网络,通过流量平衡原理来保证各区域的连通性。 式中:yijc,gd为线路在分区gd中的流量值;zi,gd为0-1变量,表示节点i在分区gd中的带电状态。 式(29)为源点的流量平衡方程,确保各子系统中源点发出的流量恰为各汇点所需的流量之和;式(30)保证各汇点的流量平衡;式(31)对支路上的流量大小进行限制。 (3)非同调群分离约束 除了同调机组的连通性约束外,还必须保证非同调机组不连通。 式(32)用来保证每个节点只属于一个分区,且没有孤立节点存在。当机组分群确定后,同调机组在同一区域带电,非同调机组在不同区域带电。式(33)表示每条线路要么在某分区投运,要么被断开,被断开的一组线路即为割集,共同构成最优解列断面。式(34)和式(35)表示只有当线路两端节点在同一区域带电时,线路在该分区投运,否则不投运。 此外,针对各分区均建立一组形如式(15)至式(21)所示的MISCR 约束,并在建立的受端电网主动解列模型中计及,即构成一个典型的混合整数线性规划模型,可采用商用优化求解器求解。 李志文(1963—),女,辽宁朝阳人,教授,博士生导师,研究方向为海洋法和海事法。E-mail:lizhiwen@dlmu.edu.cn 为进一步优化电网运行,提升系统经济性,通过开断规定数量的输电线路即可有效降低系统发电成本[22]。在面向交直流受端电网进行OTS 决策时,向优化模型中引入MISCR 约束,能够有效确保受端交流网架对直流运行的电压支撑能力。 1)OTS 目标函数 式 中:f为OTS 目 标 函 数 值;cg为 发 电 机g的 单 位 发电成本;ck为开断单条线路的操作成本。式(36)由发电成本和线路开断成本共同组成。 2)OTS 约束条件 在OTS 的寻优过程中,希望断线操作不会破坏整个网架的连通性。由于伴随网络中的支路状态与原网架一一对应,因此将网络流理论直接应用于伴随网络,即可保证原网络的连通性。首先,以伴随网络中电流源所在节点为源点,其他节点为汇点构成单源多汇网络。那么,除发电机接地点外,其他任意节点都因为受到电流源的作用建立起高于零电位的节点电压。因此,通过式(37)即可保证网络拓扑的连通性。 由此可见,在单源多网模型中,通过对各伴随网络中的节点电压加以限制,便可实现连通性约束的建模。而在多源双网模型中,伴随网络中含有多个源点,即使是在网架不连通的情形下,只要各子系统中存在至少一个源点,便可使全网建立起大于零的节点电压。此时,式(37)所示的连通性约束不再有效。因此,需要重新构建一个仅含单位电流源注入的伴随网络,通过限制电压大于零来保证全网的连通性。至此,多源双网模型的“双网”已全部构建完成。 除连通性约束外,再将式(23)至式(28)修改为不考虑分区的直流潮流约束[5],并引入式(6)至式(12)或式(15)至式(21)所示的MISCR 约束,即可完成混合整数线性规划模型的建立。 为说明本文所提MISCR 建模方法的有效性,本章基于通用代数建模系统(GAMS)平台搭建了主动解列模型和OTS 模型,并利用CPLEX 求解器进行求解。所有测试均在配置为Intel Core i5-6200 CPU、8 GB 内存的PC 上进行。 该模型采用IEEE 39 节点系统进行测试,假设在节点5、14、18 处分别馈入500、800、600 MW 的直流传输功率,具体拓扑如图6 所示。 图6 修改后的IEEE 39 节点系统Fig.6 Modified IEEE 39-bus system 假设系统遭受严重故障后失稳,发电机分为2 个同调机群:机组30、31、32、37、39 为一同调机群,剩余机组为另一同调机群。为防止事故进一步扩大,此时需要寻求最优解列断面,将系统解列为2 个孤岛运行。以故障后的总负荷损失最小为目标求得初始解列断面由线路25-26、17-18、14-15 组成,如图6 中的方案1 所示。引入本文所提的MISCR 约束后,得到的最优解列断面由线路25-26、3-18、15-16 组成,如图6 中的方案2 所示。为说明本文所提方法在网架拓扑决策优化中的有效性,现将MISCR 约束引入前后2 种解列方案的测试结果在表1 中进行对比。 观察表1 可知,采用原始模型求得的解列方案将直流落点5、14、18 划入同一子系统,且各换流母线节点处的MISCR 均小于3。这表明该子系统的受端交流网架过于薄弱,不具备同时支撑3 回直流稳定运行的能力,未考虑安全约束得到的决策方案可能使含有直流馈入的孤岛承受一定的运行风险。当计及MISCR 约束后,求得的最优解列断面将完整网架分成了2 个独立运行的小型交直流系统。其中,左侧区域是含有直流落点5 和14 的双馈入系统,右侧区域为仅含有直流落点18 的单馈入系统。由各换流母线处的短路比指标均大于3 可知,解列后的2 个孤岛对于馈入本系统中的直流都有着足够坚强的电压支撑能力,这大大降低了直流换相失败的风险,更加有利于后续的系统恢复。 表1 2 种主动解列方案结果对比Table 1 Comparison of results with two active splitting schemes 由此可见,本文所提约束可以有效确保电网拓扑优化后各换流母线处的MISCR 始终在允许范围内,减小直流发生换相失败故障的概率,因而在交直流受端电网的紧急控制方案决策中具有一定的实用价值。即使是在系统多处不连通的工况下,所提模型依然能够跟随网架拓扑的变化正确反映各直流落点的短路比情况,具有良好的适应性。 本节采用修改后的IEEE 118 节点系统作为算例[23]对OTS 模型进行测试。该系统中的直流落点为节点49、66,馈入功率均为800 MW,具体系统结构见附录A 图A2。 在网架全接线的初始状态下,节点49、66 处的MISCR 分别为3.333、3.012,受端电网结构较为坚强。为进一步提升电网运行的经济性,期望通过合理的开断操作改善原有的网架拓扑。在借助OTS模型确定开断方案的过程中,为避免触及交直流系统的安全运行底线,向模型中加入本文所提约束,以保证各直流落点处的MISCR 始终在阈值内。为说明该约束在决策中所起的重要作用,现将模型测试结果记录在表2 中。 表2 约束引入前后双馈入系统的模型测试结果Table 2 Model test results of double-feed system with and without constraints 由表2 可知,当允许开断的线路数目一定时,不含约束的OTS 模型给出的开断方案会使系统的MISCR 指标有不同程度的下降,KMISCR,66甚至跌落到3 以下。此时,交流网架对于直流的支撑能力较弱,电网的安全运行可能受到威胁。而考虑短路比约束后得到的网架拓扑决策方案可以有效确保系统结构经调整后仍然具备足够的电压支撑能力,避免了由于线路开断导致的受端网架强度下降,从而降低了直流换相失败的风险。由此可见,在面向交直流系统的受端网架拓扑优化过程中,有必要对各直流落点的MISCR 加以限制,由此保障系统的安全稳定运行。 另外,IEEE 118 节点系统还设置了3 回直流馈入的场景,除节点49、66 外另增设一回直流落点92,所接入直流的传输功率为800 MW。利用OTS 模型对上述场景进行测试,并将结果记录在表3 中。 表3 约束引入前后三馈入系统的模型测试结果Table 3 Model test results of triple-feed system with and without constraints 观察表3 可知,在允许开断数目一定的前提下,相比于约束引入之前,节点49、66 处的MISCR 指标在约束引入后有了明显的提升,说明在涉及网架调整的运行优化模型中计及MISCR 约束,能够有效确保交直流系统的稳定运行。由此可见,本文所提约束对于受端电网的安全性保证具有一定的实用价值。 网架拓扑调整作为受端电网设计规划、运行与控制中常见的优化措施,可能对MISCR 产生明显影响。为此,本文研究提出了一种受端电网拓扑决策优化中MISCR 约束的线性化建模方法。通过构建与原网架拓扑相似、支路开断状态随动的伴随网络,实现了MISCR 与支路开断状态映射的线性化解析表达。 基于所提方法,建立了计及MISCR 约束的受端电网主动解列和OTS 问题的混合整数线性规划模型,算例结果验证了该模型的正确性和有效性。此外,本文分析证明了基于伴随网络的节点阻抗建模方法能够在决策过程中保持MISCR 随系统结构的变化关系,不仅适用于运行优化中的网架微调,还适用于主动解列这样网架拓扑不连通的情形,为受端电网规划、运行控制中共性安全约束的建模问题提供了参考。即使是在网架极度残缺的场景下,本文所提方法也依然适用。因此,考虑MISCR 约束的受端电网在大停电后的网架重构问题将是下一步重点研究内容。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。2.2 基于多源双网的MISCR 约束建模

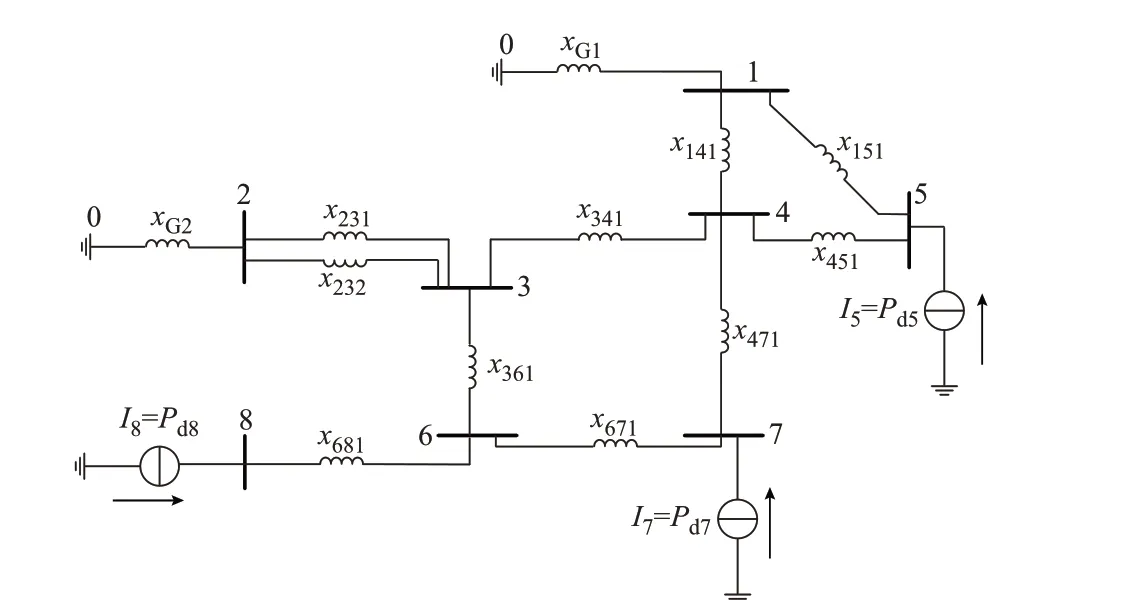
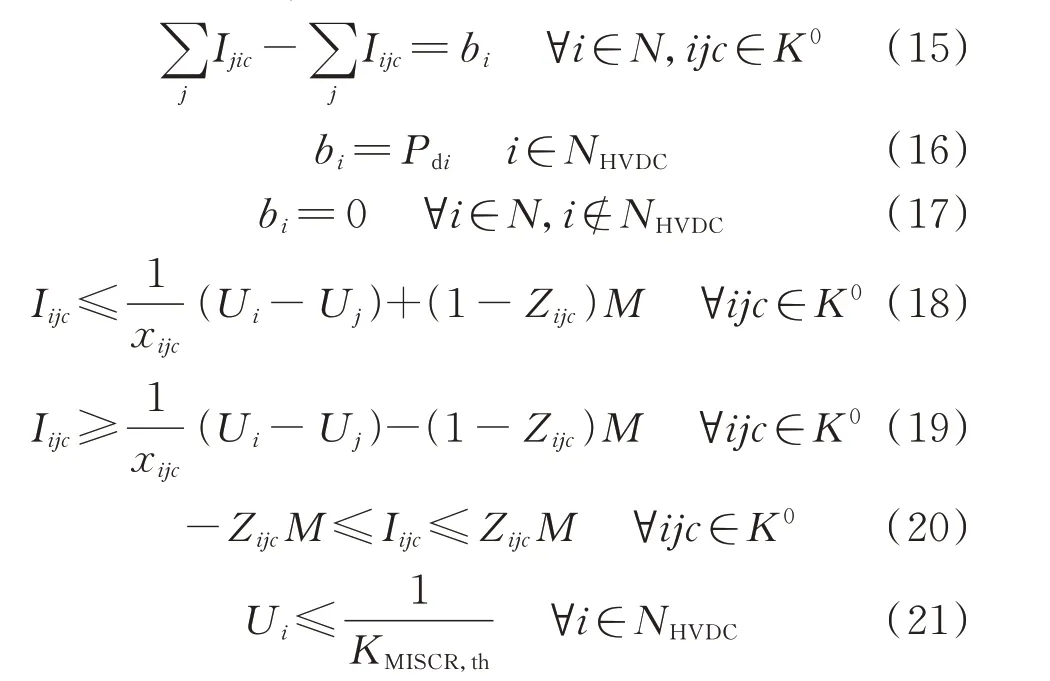
2.3 网架不连通情况下的适用性分析
3 含MISCR 约束的网架拓扑优化模型
3.1 严重故障后的主动解列问题

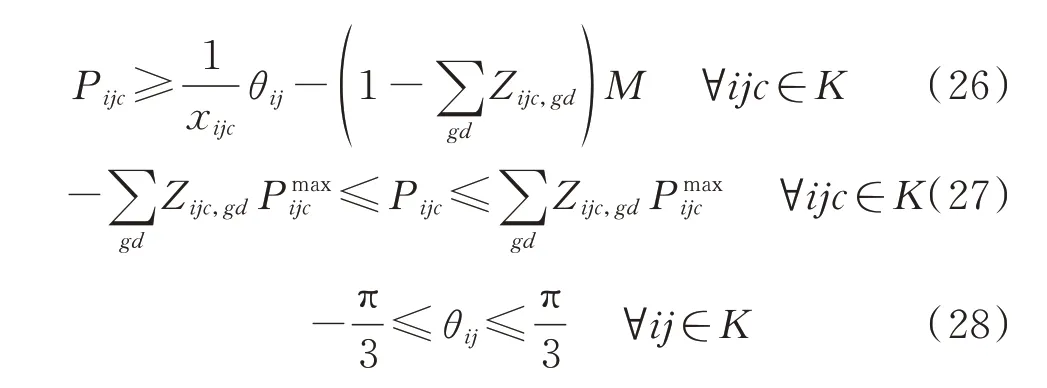
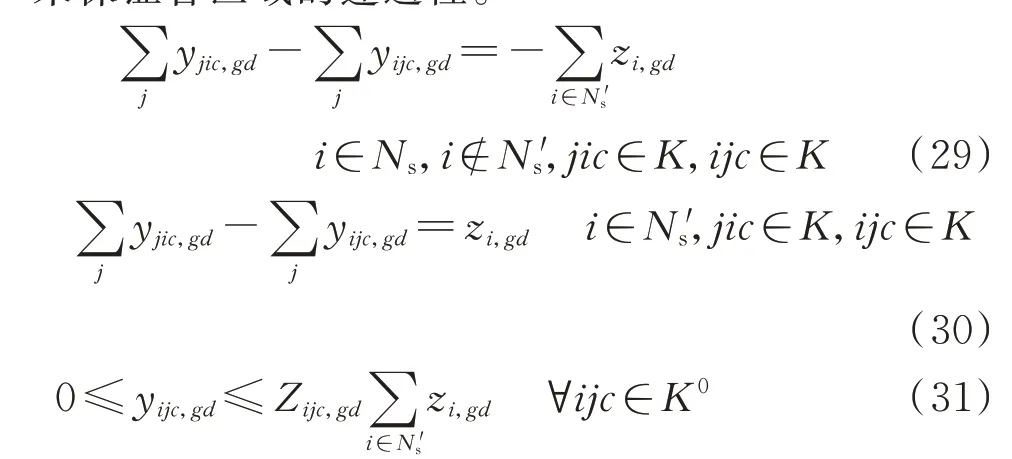
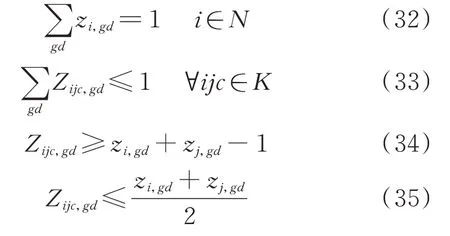
3.2 正常运行时的OTS 问题
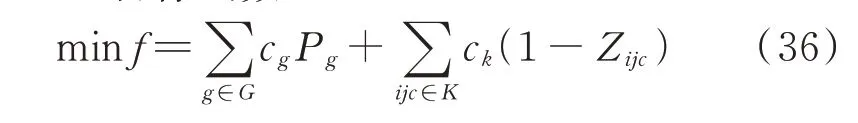
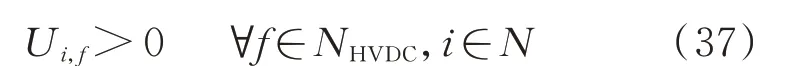
4 算例测试
4.1 主动解列模型测试结果
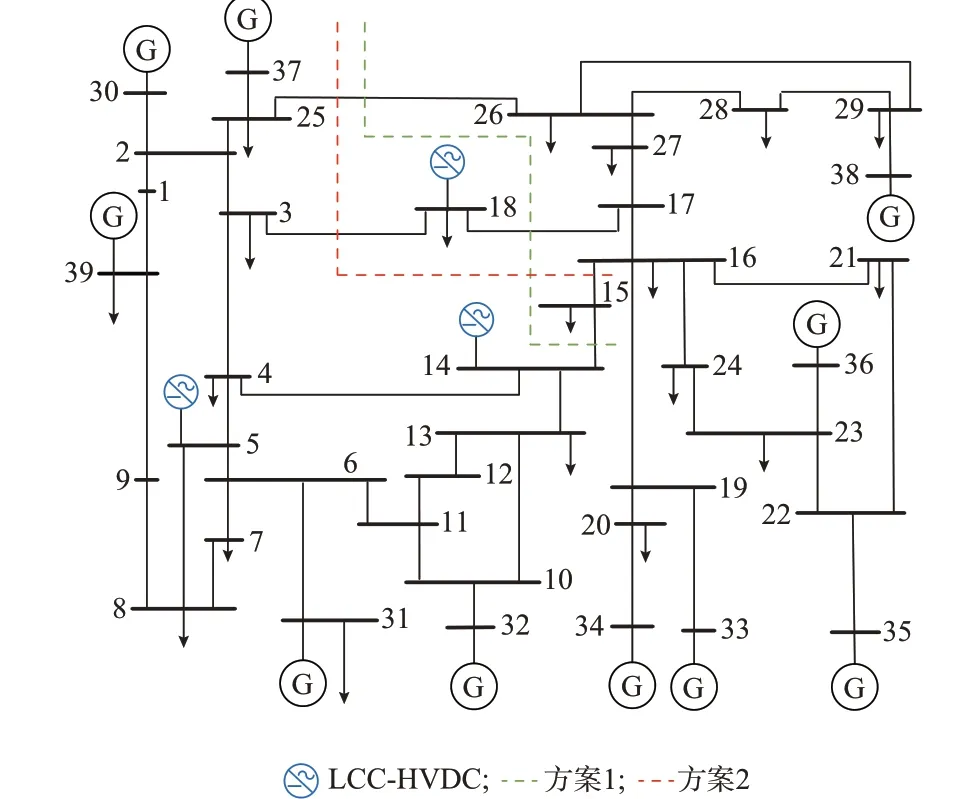

4.2 OTS 模型测试结果

5 结语

