广义位势理论本构模型的开发和验证

钟志辉，杨光华，张玉成，温 勇,官大庶

(1.广州市宏禹水利水电勘测设计有限公司，广州 511458； 2.广东省水利水电科学研究院，广州 510610；3.华南农业大学 水利与土木工程学院，广州 510642； 4.仲恺农业工程学院 城乡建设学院，广州 510225；5.广东水利电力职业技术学院，广州 510610； 6.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221008)

1 研究背景

岩土材料的本构模型是现代土力学的基本课题，是岩土工程计算的基础，其研究在世界范围内都受到很大的重视。目前为止，人们建立的岩土本构模型达数百个，但绝大部分的本构模型是基于经典的金属弹塑性理论提出的，被广泛应用的模型却较少。把复杂材料的本构模型建立在简单材料的本构理论基础上，显然有一定的局限性[1-2]。

为了突破经典弹塑性理论的局限，杨光华等[3-6]从数学角度出发，建立了材料本构模型的广义位势理论，并阐明了传统本构理论的数学实质。广义位势理论的本构模型数学依据明确、物理假设较少，因此基于广义位势理论建立的本构模型从理论上来讲更为科学和完善。近年来，通过广义位势理论构建本构模型逐渐得到更多人的研究和应用[7-14]。周爱兆等[8]基于广义位势理论建立了接触面的弹塑性本构模型；杨光华等[12]针对正常固结黏土的室内试验特征，基于广义位势理论构建了一个类似于剑桥模型的改进模型；温勇等[13]在类剑桥模型的基础上，发展了一个能考虑土体剪胀性的二重势面模型；钟志辉等[15-16]采用颗粒流软件PFC3D对广义位势理论的二重势面模型进行了验证；陆有忠等[17]提到广义位势理论虽然应用前景广阔，但仍会受到建模者的经验和土体复杂性的限制。

广义位势理论数学原理明确，即首先在主空间上数学拟合应力应变试验曲线，然后用数学势函数的方法，将主空间的应力应变关系转换成六维空间的应力应变关系，从而建立岩土材料的本构模型。然而，将广义位势理论的本构模型开发到大型数值分析软件中，并在六维应力应变空间中进行计算分析和验证的工作仍然比较缺乏[18]。为此，本文介绍了广义位势理论的本构模型及其弹塑性矩阵，以2个广义位势理论二重势面模型——不考虑剪胀性的类剑桥模型和考虑剪胀性的类剑桥模型为例，在FLAC3D中实现模型的开发，并采用开发的模型在FLAC3D的六维应力应变空间中进行计算分析。通过对比数值计算结果和室内试验结果，以验证广义位势理论本构模型的科学性和软件模型开发结果的正确性，为广义位势理论的应用提供基础支持。

2 基于广义位势理论的本构模型

2.1 多重势面模型

广义位势理论中的多重势面模型，其塑性应变增量与应力之间的关系可表示为[4]

(1)

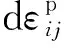
(2)

在三维主空间中，通过三轴试验可以拟合出塑性主应变εip与主应力σi的关系函数hk(σ1,σ2,σ3)，从而间接得出塑性主应变与应力σij的关系fk(σij)，即

(3)

写成增量的形式为

(4)

或写成矩阵的形式为

(5)

广义位势理论的核心就在于如何把主空间应力和应变的关系转换成六维空间的应力应变关系。在三维主空间中，根据式(1)可得

(6)

写成矩阵的形式为

(7)

联立式(5)和式(7)得

(8)

把应变增量dε分解为弹性部分dεe和塑性部分dεp，则有

{dσ}6×1=[De]6×6{dεe}6×1=

[De]6×6({dε}6×1-{dεp}6×1) 。

(9)

式中[De]为弹性矩阵。把式(2)代入式(9)求得{dσ}，再把{dσ}代入式(8)得

(10)

解方程组(10)得

其中：

(12)

(13)

|A|为矩阵A的行列式；Aik为aik对应的代数余子式。把式(8)代入式(2)后,再把{dεp}6×1代入式(9)可得

{dσ}6×1=[Dep]6×6{dε}6×1。

(14)

式中[Dep]为多重势面模型的弹塑性矩阵。式(14)为六维空间的应力应变关系。

2.2 二重势面模型

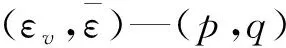
(15)

或者可以写成

(16)

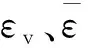
(17)

将式(17)代入式(16)得

(18)

通过三轴试验，可以拟合出二维主空间的应力和塑性应变的关系,即

(19)

式中A、B、C、D为塑性系数。

此时，式(14)的弹塑性矩阵[Dep]变为

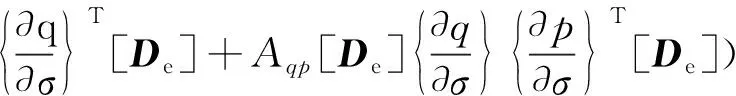
(20)

其中系数：

3 FLAC3D开发本构模型简介

本文以FLAC3D为开发平台，对广义位势理论本构模型进行开发，以验证广义位势理论本构模型在六维应力应变空间计算的可行性。

FLAC3D是美国Itasca Consulting Group, Inc.公司开发的专门针对岩土工程的三维有限差分法分析软件，该程序基于连续介质的显式拉格朗日差分法，适合求解非线性大变形问题，在岩土工程数值分析领域应用较为广泛。

FLAC3D提供了一个完善的本构模型开发环境，用户自定义的本构模型可以通过C++语言编写，并以动态连接库(DLL.文件)的形式提供给主程序调用。在每一步计算过程中，主程序会提供应变增量，用户需要根据自己的本构模型计算应力增量，然后更新单元应力并返回给主程序，具体的开发步骤可参考FLAC3D用户手册和文献[19]。对于广义位势理论的本构模型，应根据式(14)或式(20)生成弹塑性矩阵，6个应力分量增量通过该矩阵与6个应变分量增量建立关系，最后根据本构方程(11)计算应力增量。FLAC3D内部计算过程如图1所示，整个过程是在六维应力应变空间中计算的。

图1 FLAC3D内部计算过程Fig.1 Internal computing process in FLAC3D

4 开发实例1——不考虑剪胀性的类剑桥模型

4.1 类剑桥模型介绍

本文以一个二重势面模型——类剑桥模型进行说明。文献[12]提出的类剑桥模型，其类似式(19)的表达形式为

(21)

其中：

(22)

(23)

(24)

式中：参数M、λ、κ与剑桥模型的参数一致，分别为极限应力比、压缩指数、回弹指数；参数n按文献[12]给出的方法确定；e为孔隙比。

弹性应变通过弹性理论求得，即

(25)

式中：Ke为弹性体积模量；Ge为弹性剪切模量。Ke一般通过等向回弹试验确定，即

(26)

根据弹性理论，Ge可表示为

(27)

式中μ为泊松比，一般可取0.3。可见，主应力空间的应力和应变的关系为

(28)

通过式(20)和式(14)即可转换为六维空间的应力应变关系。

4.2 类剑桥模型“屈服面”推导

由于类剑桥模型满足关联流动法则，因此可以将塑性势面代替屈服面，通过屈服面来确定加卸载准则。根据式(21)，类剑桥模型的塑性应变增量方向为

(29)

设屈服轨迹为f(p,q,H)=0，由一致性条件可得

(30)

根据关联流动法则，可得

(31)

联立式(29)—式(31)得

(32)

解微分方程(32)得

(33)

式中p0为等向固结压力，可以视为该屈服面的硬化参数。

4.3 算例验证

在FLAC3D中对类剑桥模型进行开发。为了测试开发的类剑桥模型的计算精度，本节采用开发的类剑桥模型在FLAC3D中模拟土单元在三轴压缩受力状态下的应力和应变，并与文献[20]提供的正常固结黏土的三轴试验结果进行比较。土样参数如表1所示，表1中的参数n根据文献[12]提出的方法确定，e是300 kPa固结压力下的孔隙比。

表1 算例1的计算参数Table 1 Parameters for computational example 1

为了同时考虑网格单元数量的影响，数值模型分别采用了单个网格单元和多个网格单元。单网格模型为1个边长600 mm的立方体brick单元(见图2(a))；多网格模型为8个边长300 mm的立方体brick单元(见图2(b))。两个模型都采用相同的边界条件：模型底面约束竖向位移；侧面采用应力边界条件，围压300 kPa；模型顶部的轴压分级施加，每一级增加5 kPa。

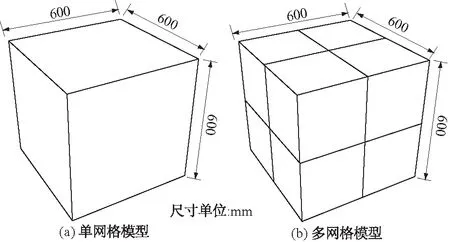
图2 FLAC3D中的计算模型Fig.2 Computational model in FLAC3D

图3为试验结果与数值模拟结果的比较，图3中分别有试验数据、式(28)的拟合结果、单网格模型的计算结果和多网格模型的计算结果。

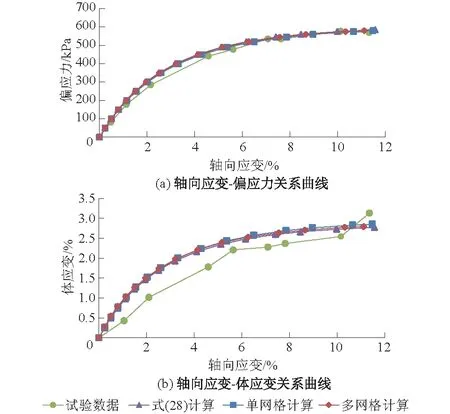
图3 常规三轴压缩试验结果与模拟结果对比Fig.3 Comparison between conventional triaxial compression test results and simulated results

由图3可见：

(1)类剑桥模型在主空间的应力应变拟合曲线，即式(28)，能够较好地反映试验结果，说明类剑桥模型在主空间的应力应变拟合关系是合理的。

(2)将六维空间的应力应变关系，即式(11)，开发到FLAC3D进行数值计算，无论是单个网格计算还是多个网格计算，得出的数值计算结果与式(28)的计算结果十分接近，说明了广义位势理论对主空间和六维空间的应力应变关系的转换方法是可行的，同时也说明了在FLAC3D中开发的类剑桥模型是正确的。

(3)理论上FLAC3D的计算结果应该与式(28)的计算结果完全一致，但由于数值模拟精度与网格单元的类型和数量有关，数值模拟难免存在计算误差，若增加网格密度，计算误差会进一步减少。

5 开发实例2——考虑剪胀性的类剑桥模型

5.1 考虑剪胀性的类剑桥模型

第4节的类剑桥模型不能反映土体的剪胀性，文献[13]在类剑桥模型的基础上，提出了一个能考虑土体剪胀性的二重势面模型，该模型在主空间的塑性应变与应力的关系表达式为

(34)

其中：

(35)

(36)

式中:A与式(22)一致；M为特征状态应力比;Mf为峰值强度时的应力比，两者定义参考文献[20]。主空间应力和应变的关系为

(37)

通过式(20)和式(14)即可转换为六维空间的应力应变关系。

5.2 算例验证

采用文献[21]—文献[22]提供的试验数据对上述模型进行验证。土样参数如表2所示，表2中的参数n根据文献[12]提出的方法确定，e是196 kPa 固结压力下的孔隙比。计算网格仍采用如图2所示的网格，围压196 kPa，单元顶部的轴压分级施加，每一级增加5 kPa。

表2 算例2的计算参数Table 2 Parameters for computational example 2

图4为试验结果与数值模拟结果的对比，可见两者的轴向应变-偏应力关系曲线十分接近，而两者的轴向应变-体应变关系曲线有一定差异，但在允许范围内。结果表明该本构模型在一定程度上能反映土的剪胀性，计算结果较为合理。

图4 常规三轴压缩试验结果与模拟结果对比Fig.4 Comparison between conventional triaxial compression test results and simulated results

可见，在FLAC3D六维空间中的计算结果，跟主空间的应力应变计算结果(即式(37))几乎重合，说明了广义位势理论对主空间和六维空间的应力应变关系的转换方法是合理可行的，同时也表明该本构模型在FLAC3D中的开发是成功的。

6 结 论

广义位势理论从数学角度出发，给出了从主空间应力应变的关系转换成六维空间的应力应变关系的方法，数学依据明确，物理假设少，因此在广义位势理论基础上建立的本构模型更为科学和完善。

本文在数值分析软件FLAC3D中开发了广义位势理论基础上的2个二重势面模型——不考虑剪胀的类剑桥模型和考虑剪胀的类剑桥模型，通过三轴试验成果对FLAC3D开发的类剑桥模型进行验证，结果表明：基于开发的本构模型得出的数值计算结果与试验结果较为接近，由此说明了2个类剑桥模型的合理性和模型开发的正确性。同时也验证了广义位势理论中把应力应变关系从主空间转换到六维应力应变空间的方法是可行的。