面向纹理平滑的方向性滤波尺度预测模型

林俊彦，刘春晓，章金凯，李泓易

浙江工商大学计算机与信息工程学院, 杭州 310018

0 引 言

纹理滤波旨在通过保留物体的结构和平滑不重要的纹理对图像进行滤波，这是一个底层视觉算法问题，并在细节增强、色调映射、去噪和边缘提取等领域有着重要的实用价值。

已有的纹理滤波方法可以分为两大类，即图像处理方法和深度学习方法。图像处理的纹理滤波方法又可以分为局部滤波和全局滤波两类。局部滤波方法通过局部滤波核计算纹理像素的邻域平均值，同时试图保留结构像素的原始值，如He等人(2010)提出的引导滤波(guided filtering，GF)，Zhang等人(2014)提出的滚动引导图像滤波(rolling guidance filter，RGF)，Zhang等人(2015)提出的基于分割图的图像滤波(segment graph based image filtering，SGF)，刘春晓等人(2018)提出的基于半高斯梯度算子的尺度自适应纹理滤波。局部滤波的方法往往能以较快的速度得出平滑结果，但是效果不是很理想。而全局滤波的方法通过寻求含有数据约束项和先验平滑项的目标函数的最优解来进行纹理滤波，如Xu等人(2012)提出的相对总变分(relative total variation，RTV)，Xu等人(2011)提出的L0梯度最小化方法，Ham等人(2018)提出的鲁棒引导图像滤波(static/dynamic filter，SDF)，邵欢和刘春晓(2018)提出的结合纹理梯度抑制与L0梯度最小化的纹理滤波。这些方法往往能得到较好的运行结果，但是速度较慢。现有的基于图像处理的纹理滤波方法难以在滤波强梯度纹理的同时较好地保持结构，并且大多数此类方法都需要经过复杂的超参数调整。

目前已有许多基于深度学习的纹理滤波方法， Xu等人(2015)的深度边缘感知过滤器(deep edge-aware filters，DEAF)和Fan等人(2017)提出的级联边缘和图像学习网络(cascaded edge and image learning network，CEILNet)在模型表示方面有相似的思想，即先求出物体的结构，再求出最终的滤波结果。Zhu等人(2019)提出的边缘保持图像平滑的基准模型(benchmark for edge-preserving image smoothing，BEPS)，在没有任何先验知识的前提下，使用残差网络进行端对端的训练。虽然训练方式简便，但会给模型拟合带来困难。上述方法都是在以现有非深度学习方法产生的结果为标签的基础上进行训练的，相较于复杂的非深度学习方法，运行速度较快，同时也能得到不错的性能，但是无法克服现有非深度学习方法的不足。其中BEPS是此类方法的代表，它以多种图像处理方法的结果为标签，分别计算损失函数并根据视觉平滑效果人工确定混合权重。虽然BEPS的训练方式可以得到综合性能较好的模型，但是当所有图像处理方法都对某些纹理失效时，BEPS也不会得到好的结果，并且这类方式工作量巨大。Fan等人(2018)提出了基于无监督学习的图像平滑，这种方法利用一个可以自动鉴别纹理的能量函数对模型进行训练，但其鉴别方式较为简单，不能广泛地涵盖所有纹理，因此在纹理鉴别的时候性能会受到一定约束。它的网络结构与BEPS类似，都是较深的单阶段卷积神经网络，所以其模型表示方式的缺点也与BEPS类似。Lu等人(2018)提出了纹理和结构敏感的图像平滑网络(texture and structure aware filtering network，TSAFN)，借助自己合成的数据集来训练提出的网络模型。然而，它以卡通图像等缺乏纹理的图像作为图像平滑标签，在此基础上整体添加纹理细节生成待平滑图像。这样的数据集合成方式存在两个问题：1)标签方面，TSAFN中纹理细节移除后的图像平滑标签与目前主流方法所追求的纹理和背景的平滑颜色不一致。2)纹理方面，TSAFN在整幅图像上覆盖同样的纹理，而自然图像中的纹理是因物体而各异的。因此，TSAFN合成的数据集不但与真实图像有较大的域差异，而且不符合主流的纹理平滑期望。

1 本文算法

针对目前图像平滑方法在平滑强梯度纹理与保持物体结构上性能较差，深度学习方法缺少可使用的数据集与其模型表示方式比较粗糙的问题，本文在现有结构图像的基础上，通过逐连通区域填充不同形式的纹理和对物体边缘进行多种处理的方式，生成了一个面向深度学习的纹理滤波数据集。随后，本文设计了一个由尺度感知子网络和图像平滑子网络组成的基于方向性纹理滤波尺度预测模型的图像平滑网络。其主旨是先通过尺度感知子网络得到滤波尺度图，该图不但包含了某一像素与周围像素是否为同一纹理的要素，而且还隐含了某一像素是否为结构像素的信息。然后将滤波尺度图与原图堆叠作为图像平滑子网的输入进行纹理滤波。图1为本文算法的流程图。

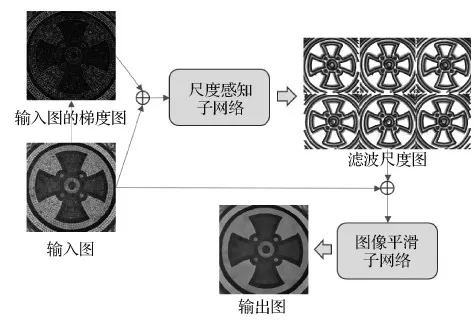
图1 本文算法流程图Fig.1 The flowchart of our algorithm

1.1 纹理滤波数据集

本文在现有取自DUTS(Dalian University of Technology Saliancy)(Wang等，2017)、THUR(Tsinghua University region)(Cheng等，2014)和显著目标检测数据集(salient object dataset，SOD)(Movahedi和Elder，2010)(图2(a))的结构图像的连通区域中随机填充1 089种纹理图的一种(图2(b))，纹理图来自描述纹理数据集(describable texture dataset，DTD)(Cimpoi等，2014)，这些纹理图有不同的梯度与形式，可以有效增强模型对于不同纹理的平滑能力。而对应的标签图(图2(c))就是在相同连通区域填充对应纹理图的平均颜色。纹理图以及平均后的纯色图见图2(d)。本文共生成15 086幅训练图以及对应标签图。

图2 本文纹理滤波数据集的构造Fig.2 Construction of our texture filtering datasets((a)structure map; (b)training image; (c)ground truth image; (d)texture images and corresponding pure color images)

在上述设置下，本文制作的面向深度学习的纹理滤波数据集不仅有利于增强算法对于强梯度纹理与结构的区分能力，而且还减小了合成数据与真实数据的域差异。

1.2 尺度感知子网络

由于目前深度学习方法的模型表示方式本身比较粗糙，所以本文采用一种更加细致有效的模型表示方式：即使用尺度感知子网络来逐像素预测Dn幅滤波尺度图。Dn幅滤波尺度图代表Dn个方向的滤波尺度，在本文中，方向数量Dn设置为6。设置滤波尺度的最大值为p，当滤波尺度大于最大滤波尺度p或者超出图像边界时，将其设置为p，设置p值为21，相对应，本文网络输出值的范围为[p,1]，在归一化处理后为[1/p,1]。

纹理大多体现在低级特征上，而U-Net(Ronneberger等，2015)具有优秀的利用低级特征的能力。因此，将U-Net作为本文网络结构。如图3所示，U-Net的左侧是压缩路径，右侧是扩展路径。压缩路径由4个块组成，每个块都含有3个卷积层和1个最大池化层，每次池化后特征图的长和宽都会缩小为原特征图的1/2，并且特征图的数量也会增加为原特征图的两倍。扩展路径同样由4个块组成，每个块包含1个反卷积层和3个卷积层，反卷积层将特征图数量减少为原特征图的1/2，长和宽增加为原特征图的两倍，第1个卷积层的输入特征为扩展路径的特征图和压缩路径对应尺寸的特征图的堆叠。由于本文设置的方向数量为6，所以输出一共有6个通道，代表6个方向的滤波尺度。扩展路径的最后一个块的反卷积层被替换为1×1的卷积层，卷积后输出6幅滤波尺度图。因为纹理在梯度中往往有更加直观的反映，添加梯度信息有利于模型对于滤波尺度的预测，所以输入一共有4个通道，分别是RGB图像和它的单通道梯度图。

图3 尺度感知子网络的结构Fig.3 Structure of scale-aware sub-network

尺度感知网络的尺度标签是根据训练图的对应标签图制作的(图2(c))。注意，本文方向顺序是顺时针的。在标签制作中，标签图中一个像素点i在某方向时，若在最大边长为t、角度为360°/Dn的扇形中没有其他颜色的像素值出现，则该像素点i在该方向的纹理尺度为t，当t大于p或者达到图像边缘则直接设为p。注意，在纹理图中，相邻的连通区域不会用同一平均颜色的纹理填充，所以这个方法不会出现意料外的情况。以图4为例，不规则线条连接而成的连通区域表示结构，扇形的顶点代表选中的像素，圆形代表该点6个方向同时都是最大滤波尺度时的情况。在该像素点上各个方向的滤波尺度就是图中各个方向扇形的边长。可以简单地把扇形区域理解为该方向滤波器的形状。也就是说，如果某像素值在方向0的尺度为5，则该像素在顺时针方向[0,π/3]处边长为5的扇形区域内不包含别的纹理像素。

图4 6个方向的滤波尺度Fig.4 Filtering scales in six directions

通过观察可以发现，尺度感知子网络预测得到的滤波尺度图比结构图更加细致，能够在模型训练过程中起到较强的约束作用，从而有利于模型的快速收敛。

(1)

式中，Lsa就是尺度感知网络的损失函数，N代表不同方向的尺度图数量，Num代表图像中像素的数量，S′代表尺度标签，S代表网络输出图像。

图2所示图例的滤波尺度图标签在归一化后如图5所示。

图5 尺度感知子网络的标签Fig.5 Ground truth of scale-aware sub-networks((a)direction 0; (b)direction 1; (c)direction 2; (d)direction 3; (e)direction 4; (f)direction 5)

1.3 图像平滑子网络

在获得像素级的各方向的滤波尺度信息后，已经可以根据其平滑图像，如图4中像素点的纹理滤波后的值就是图中所有扇形内的像素平均值。但这样计算速度过慢，而且预测结果不可能绝对准确，因此，本文将滤波尺度图和原图堆叠，通过额外的几层卷积来进行平滑，以加快计算速度，并对尺度感知网络的结果进行修正。采用的网络结构如图6所示，其中Conv代表卷积层，括号内的数字分别代表卷积核的长、宽、输入层数和输出层数，除了最后一层卷积层，每个卷积层后都有ReLU激活函数层和批处理层。

图6 图像平滑子网络的结构Fig.6 Structure of image smoothing sub-network

(2)

式中，Lis就是纹理滤波网络的损失函数，D代表RGB图像的3个通道，Num代表图像中像素的数量，I′代表纯色图标签，I代表网络输出图像，g(·)代表图像梯度计算函数。纹理滤波网络的损失函数是L1损失和梯度损失。使用L1损失的原因是其优秀的颜色保持能力，能较好还原出滤波后的颜色；使用梯度损失是为了使模型更注重边缘处的平滑表现。

2 实验结果与讨论

本文算法基于Pytorch实现，训练以及测试都在单张NVIDIA RTX 2080显卡上进行。

2.1 数据集的使用

本文使用自建数据集，共15 086对训练图像对，其中1 500对作为验证集，1 000对作为测试集，训练时将数据集统一裁剪为224×224像素。

2.2 训练设置

本文的尺度感知子网络与图像平滑子网络都采用随机梯度下降方法，其中批尺寸为10，初始学习率设置为0.01，动量为0.9，权值衰减为0.000 2，学习率的下降策略为：每5个轮次(epoch)学习率下降一半，尺度感知子网络训练50轮次(epoch)，图像平滑子网络训练100个轮次(epoch)。

2.3 训练曲线及分析

本文模型的训练曲线如图7所示，图7(a)为尺度感知子网络的训练曲线，蓝色实线为训练曲线，红色虚线为验证曲线，loss为L2损失(式(1))。通过两个曲线的对比可以发现，验证损失仅略高于训练损失，因此模型在训练过程中没有出现过拟合的现象。随着轮次(epoch)的增多，训练集的平均损失值也在逐渐下降，在20个轮次(epoch)之后训练曲线下降得较为缓慢。图7(b)为图像平滑子网络的训练曲线，loss为L1损失和梯度损失的结合(式(2))。通过对比可以发现，模型在训练过程中没有出现过拟合现象，训练集的平均损失值逐渐下降，在最后20个轮次(epoch)趋于平缓，验证集的平均损失值虽然也有波动，但也在逐渐下降，没有与训练集的平均损失值产生较大的偏差。

图7 模型的训练曲线Fig.7 The training curves of our model((a) scale-aware sub-network; (b) image smoothing sub-network)

2.4 与现有模型的方法对比

将本文方法与7个经典方法进行对比，其中5个为图像处理方法，分别是L0梯度最小化方法(Xu等，2011)、RTV(relative total vriation)(Xu等，2012)、GF(guided filtering)(He等，2010)、RGF(rolling guidance filter)(Zhang等，2014)和SDF(static dynamic filter)(Ham等，2018)；2个为深度学习方法，分别是DEAF(deep edge-aware filters)(Xu等，2015)和BEPS(benchmark for edge-preserving image smoothing)(Zhu等，2019)。对比的指标为峰值信噪比(peak signal to noise ratio,PSNR)、结构相似度(structural similarity,SSIM)、均方误差(mean squared error,MSE)和运行时间。对于图像处理方法，本文使用开源代码中的默认参数进行计算。对于深度学习方法，所有模型都会在本文生成的数据集上进行重新训练。

如表1所示，在与其他方法的对比中，本文方向性纹理滤波尺度预测模型的峰值信噪比和结构相似度都达到了最大值并且均方误差与运行时间都达到了最小值。在本文数据集中进行视觉对比发现，许多图像处理方法在面对一部分纹理时会有优秀的滤波效果，但是面对另一部分纹理时，表现会较差，而本文方法不会有这种缺陷。观察图8的合成图1与合成图2，可以看出，SDF在面对大多数纹理时可以展现出相对较好的性能，但是有时会出现纹理滤波不彻底的情况，并且可能会产生严重的边缘模糊。

表1 不同模型在本文纹理滤波数据集中的性能表现Table 1 The performance of different algorithms on our texture filtering dataset

图8 本文方法与其他方法在本文自建数据集上的效果对比Fig.8 Comparison of different texture filtering methods on our dataset((a)input; (b)SDF (Ham et al., 2018); (c)L0 (Xu et al., 2011); (d)GF (He et al., 2010); (e)RTV (Xu et al., 2012); (f)RGF (Zhang et al., 2014); (g)DEAF (Xu et al., 2015); (h)BEPS (Zhu et al., 2019); (i)ours; (j)ground truth)

L0在两组图像上的表现较不理想，它对于梯度较弱的纹理有一定的抑制作用，但是对于较强梯度的纹理并不能有效滤波。RTV虽然在合成图1上表现较好，极其接近标签，但是在合成图2上，面对强梯度的纹理，RTV对纹理的滤波效果就会大打折扣。基于深度学习的方法DEAF与BEPS虽然对所有形式的纹理都有不错的处理能力，但是纹理平滑和边缘保持的能力都明显不如本文方法。在运行速度一列中，可以发现，由于GPU的加速效果，深度学习方法的运行时间比大多数图像处理方法少很多。而从深度学习方法之间的对比可以发现，本文模型在具有最好的纹理滤波能力的同时，还享有最快的速度。

本文挑选了SSIM评分最高的前4个算法，在现实世界图像上与本文方法进行比较。图9中，实例1的纹理以细条纹等弱梯度纹理为主。通过观察可以发现，虽然RTV在餐桌、墙壁和地面上的弱梯度纹理中展现了良好的滤波性能，但是其错误地模糊了人物面部和书架左侧书籍的结构。RGF、DEAF和BEPS虽然不会像RTV在面部呈现较大的模糊，但是它们的结构保持得并不平整，且纹理还有一定残留。本文算法对于纹理过滤得较为干净，对于人物面部和书架左侧书籍的结构也保持得较好。实例2展示的弱梯度纹理与实例1相似，并且有许多的细小结构，RTV对于弱梯度纹理有很好的平滑能力，但是对于草坪间的分割线和飞机的机身等细小结构并不能有效保留。RGF、DEAF和BEPS对于分割线等细小结构有一定保持能力，但是保持得不平整，有毛刺感。本文算法很好地保持了草坪中的分割线，值得注意的是，飞机旁的黄线和阴影也保持得非常好，没有出现模糊现象，证明了本文算法对于细小结构优异的保持能力。实例3反映了不同算法在强梯度纹理下的表现。可以看出，RTV对于强梯度纹理表现较好，但是其对于细小的结构，即远处的树和天空的云朵保持得并不理想。RGF对于强梯度纹理表现较差，不能有效进行滤波。DEAF和BEPS虽然对强梯度纹理有一定的滤波作用，但是还是有较多残留。本文模型可以有效平滑强梯度纹理滤波，同时保持云朵和树的结构，不会产生模糊。

图9 本文方法与其他方法在真实图像中的效果对比Fig.9 Comparison between our method and other methods on real images((a)input; (b)RTV; (c)RGF; (d)DEAF; (e)BEPS; (f)ours)

因为BEPS利用了多种图像处理方法的结果混合训练，最有代表性，将官方实现的开源模型与基于本文生成的数据集重新训练的模型进行对比，如图10所示，可以明显发现重新训练的模型在马赛克纹理、强梯度纹理等多种纹理上有较好的综合表现。这证明了面向深度学习的纹理滤波数据集可以增强模型对于强梯度纹理与弱梯度或细小结构的区分能力。

图10 官方的BEPS与基于本文生成的数据集重新训练的BEPS的对比Fig.10 The official BEPS compared to BEPS retrained on our dataset((a)original images; (b)results of the official BEPS; (c)results of BEPS retrained on our dataset)

3 结 论

针对目前纹理滤波的深度学习方法缺少可使用的数据集以及图像处理方法的强梯度纹理的平滑与弱梯度或细小结构保持的平衡问题，本文生成了面向深度学习的纹理滤波数据集，该数据集通过多种策略减小了与真实数据集间的域差异，并且含有多种类型的纹理与结构，可以增强模型对强梯度纹理与弱梯度或细小结构的区分能力。针对现有深度学习方法的模型表示方式不够细致的问题，本文提出了含有尺度感知子网络和图像平滑子网络的两段式的方向性纹理滤波尺度预测模型，它具有较好的性能和较快的运行速度，并且泛化能力较强。

当一幅图像中存在尺度较大的纹理时，其中的纹理线条会被当做图像结构保持下来，导致纹理平滑不彻底。目前暂时可以通过先将输入图像缩小再进行纹理平滑，然后通过放大纹理平滑结果来解决这个问题。如何根据图像的纹理尺度动态调节滤波尺度是下一步的研究方向。