基于热平衡法的方壳电池电芯温度预测模型

吕乔，周萍，郑岳久，沈凯

（上海理工大学，上海 200093）

随着电动汽车数量不断上升，各类电动汽车安全事故也呈现多发态势，尤其是电动汽车自燃事故报道越来越多，据不完全统计，电动汽车大多在充电过程中发生自燃。因此，对充电过程电池的温度预测显得尤为重要，建立准确的电池热模型具有十分重要的意义。

研究电池热模型是研究锂离子电池热行为的最有效的方法之一。BERNARDI 等提出了具有普适性的电池系统能量平衡方程来描述电池的产热特性，被广泛应用在电池热性能的研究中。HALLAJ等使用带有集总参数的一维简化模型，对Sony US18650 电池内部温度进行模拟，在低倍率放电下，仿真结果与试验结果较为一致，但在高倍率放电下，仿真结果与试验结果出现较大误差。CHEN等搭建出具有分层结构的三维热模型，成功预测了电池内部温度分布的差异。

现有文献主要通过搭建热模型来预测低倍率充电情况下的电池内部温度，但是较少有文献研究高倍率充电情况下电池内部的温度变化，以及充电过程中电池内部与表面的温度变化，也较少有估计电池内部和表面温度的热模型得到充分的验证。

本文面向1 C 与2 C 充电场景，通过以下几方面的工作建立了热平衡法温度预测模型：

（1）进行了内置热电偶试验，采用内置热电偶的方法来测量电池内部温度，解决了大容量方形电池内部温度难以获取的问题。

（2）采用试验测量的方法，获取电池热模型输入的各项关键参数，主要包括直流内阻、比热容、各项导热系数和熵系数等参数，准确测量的热模型参数，保证了电池热模型计算的精度。

（3）基于热平衡法分别对电池表面和电池卷芯建立能量守恒方程，建立电池三维温度预测模型，实现对电芯温度精准预测以及电池各部分温度预测。

1 试验

1.1 内置热电偶试验

试验所用电池为三元锂电池，电池相关参数见表1。

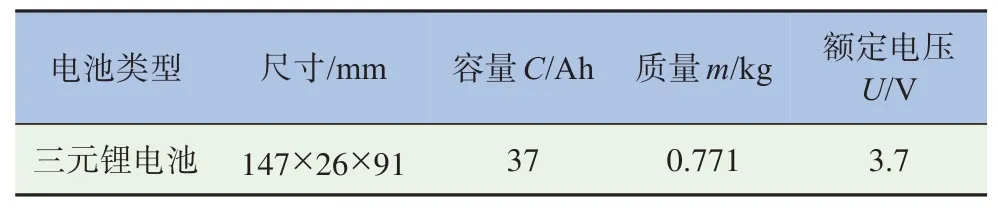
表1 电池参数

为获取充放电过程中电池的核心温度，本文选用了一种内置热电偶的方法。在内置前，先将电池放电到0%SOC，标注电池侧面的中心点，确定打孔位置，然后用电钻打出一个直径5 mm 左右的孔洞，用一根钢针探入电池内部，将卷芯之间分离出一条间隙，将铠装K 型热电偶包裹后塞入电池内部中心位置，用一小块聚酰亚胺胶带铺在开孔处的卷芯上，防止胶水进入卷芯，将无机胶涂入孔洞内，再将胶均匀涂抹在孔洞表面，竖直静置12 h，试验过程如图1所示。

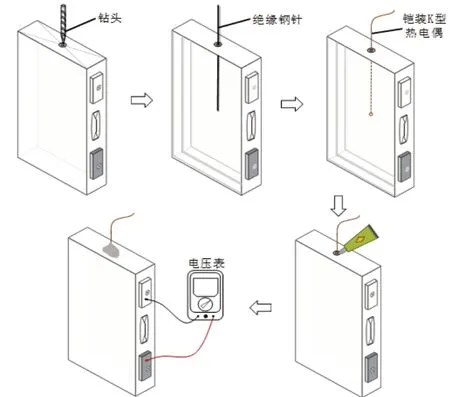
图1 内置热电偶流程

记录内置热电偶之后电池的电压，并与内置前的电压进行比较，测得电压差小于0.1 V，并在静置12 h 后再次测量电压，测得电压差仍小于0.1 V，则认为内置热电偶成功，对内置热电偶电池进行标准容量测试，测得容量损失不超过3%，因此，认为内置热电偶后的电池是有效的。

1.2 电池等效内阻测试

本文采用混合动力脉冲能力特性（Hybrid Pulse Power Characteristic，HPPC）试验测试电池等效内阻。在25°C 环境下对内置热电偶电池进行了1 C、2 C 充电倍率的HPPC 测试，每隔10%SOC 对电池施加一次脉冲，所测等效内阻如图2所示。

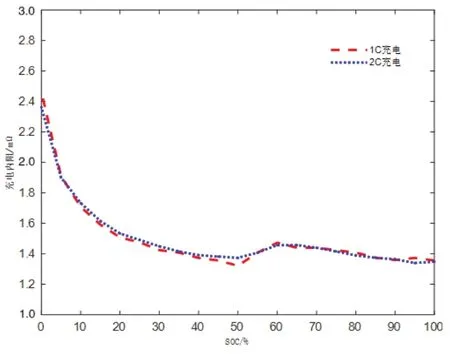
图2 内置热电偶电池等效内阻

1.3 电池比热容测试

电池的比热容是电池热模型中十分重要的参数之一，采用内置加热片的方式对比热容进行测试。首先在干燥的房间中拆解电池，在加热片中心处粘贴一个热电偶，在电池卷芯表面中心处布置一个热电偶，将加热片放入两卷芯之间，用铝塑膜重新封装电池，然后在电池表面中心处布置一个热电偶，如图3 所示。将电池置于绝热环境中，对加热片进行加热并开启温度数据采集仪，试验过程中分别记录下加热片表面、卷芯表面和铝塑膜表面3 个热电偶处的温度数据。试验需假设在加热过程中加热片产生的热量全部被卷芯吸收，加热片传递给两侧卷芯的热量是相等的，且电池在绝热环境中无热量散失。

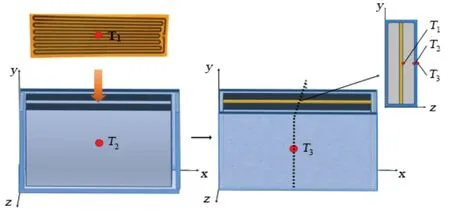
图3 比热容测试试验电池

根据能量守恒定律，可由式（1）和式（2）来计算电芯的比热容：

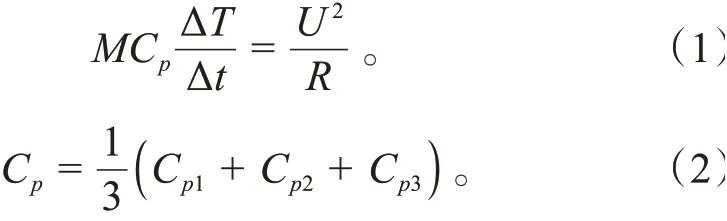
式中：为电池卷芯质量；C为电池卷芯比热容；∆为温度差值；∆为时间差值；C、C和C分别代表3个测温点处计算的电池卷芯比热容。

由式（1）计算可得3 个测温点处的比热容，由式（2）计算可得3 个结果的平均值，计算结果见表2。

表2 比热容计算结果

1.4 电池各向导热系数测试

导热系数是电池材料的重要热物理性能参数之一，严重影响着锂离子电池的各种特性。试验首先在干房中拆解电池，内置陶瓷加热片于两个卷心中间，在陶瓷加热片中心布置一个K 型热电偶，在水平方向每隔22 mm 等距离布置两个K 型热电偶和，电池卷芯表面的对应位置也分别布置3个热电偶、和，将安装好热电偶的电池用铝塑膜重新封装，再用隔热石棉包裹起来，如图4所示。对电池进行加热并分别记录下3 个热电偶处的温度数据。

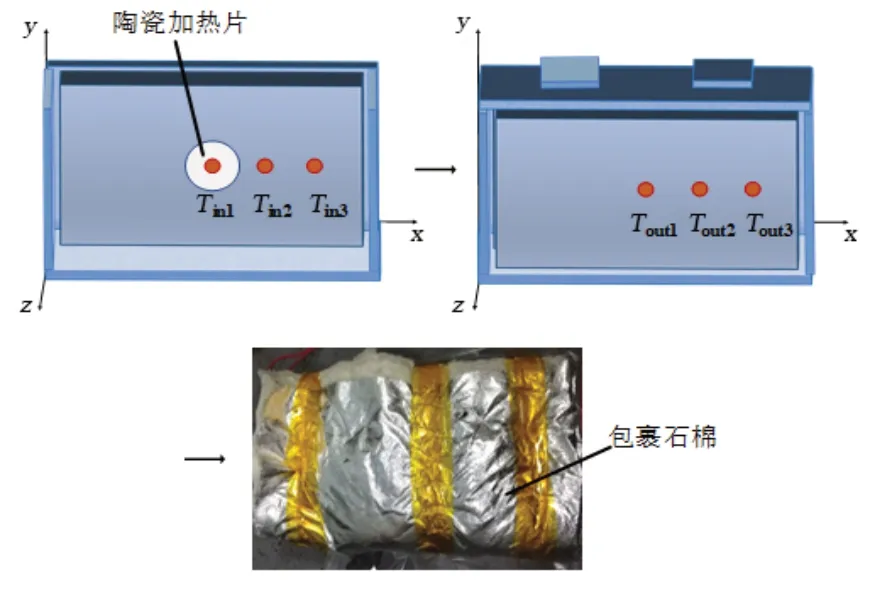
图4 导热系数测试试验电池

为了模拟导热系数测试试验过程，在Comsol中建立一个三维传热模型，对电池3 个方向的导热系数进行计算。由于电池的两块卷芯是对称的，所以只需要建立一侧的卷芯传热模型进行计算，可减少一半的计算量。所建立的卷芯模型尺寸为：长146.0 mm，高85.0 mm，厚12.5 mm，如图5所示。

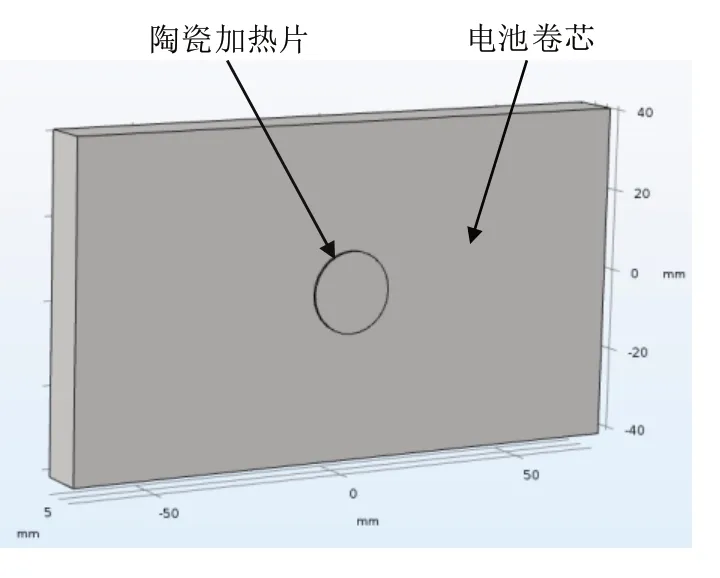
图5 卷芯三维传热模型

根据试验过程中布置的热电偶测得的温度与所建立的三维传热模型计算出的温度差值，确立优化目标函数如式（3）所示：

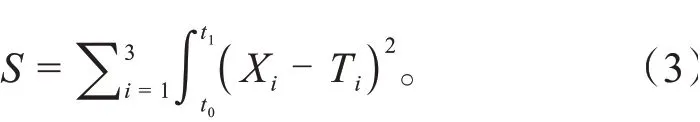
式中：X为三维传热模型的计算数据；T为试验过程中测得的数据，优化的各向导热系数：电池厚度方向导热系数λ、电池展向导热系数λ和λ，并认为λ= λ。

导热系数计算结果如图6 所示，其中虚线是模型计算结果，实线是试验结果，试验测得温度与模型计算温度较匹配，通过模型优化后的导热系数见表3。

表3 导热系数优化结果

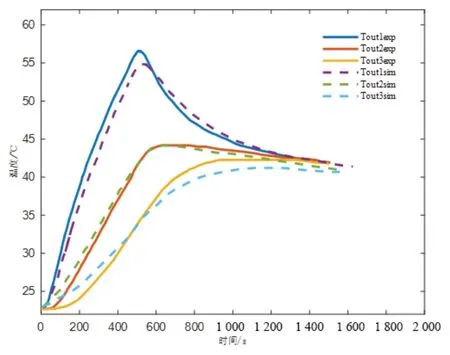
图6 模型计算结果与试验结果

1.5 电池熵热系数测试

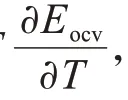
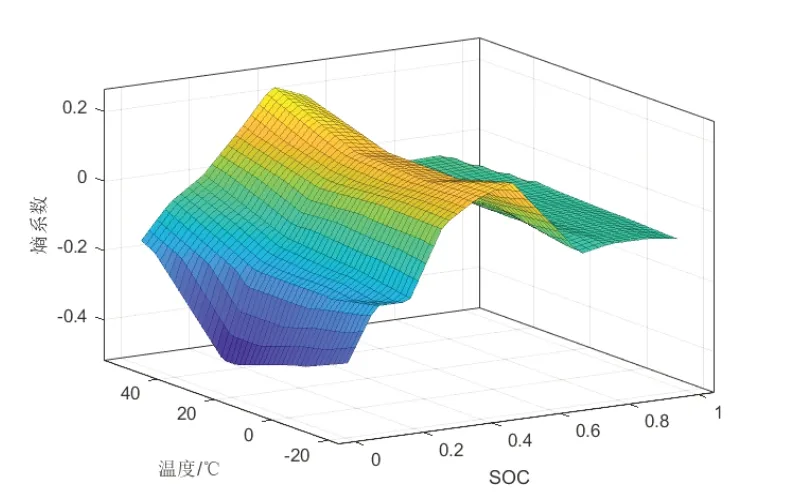
图7 熵系数测试结果

2 热平衡法温度预测模型

2.1 热平衡法模型搭建

热平衡法温度预测模型考虑电池的温度梯度变化，利用有限元的思想，把电池划分成相同等份的方块。为了准确预测电池正中心温度，以奇数为单元进行网格划分，如果选择以电池整个卷芯为一个小块无法反映出电池内部温度梯度，如果选择125个小块模型，则较复杂且计算时间成指数倍增加，因此，选定划分27 个小块，既保证中心温度估计准确性，又能实现温度的实时估计，如图8 所示。基于内节点法，以每一个小方块的中心点为目标点，分别对电池卷芯和电池表面应用能量守恒定律，建立热平衡方程，计算每一个方块的温度，也就可以获得电池每一部分的实时温度，具体流程如图9所示。

图8 电池网格模型

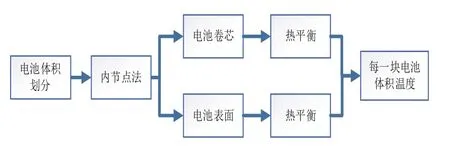
图9 热平衡法原理

电池由内部的卷芯和金属外壳组成，两者的能量增加与消散过程不同，电池内部卷芯存在热传导，电池外壳不仅存在热传导，也与空气接触产生热对流，因此，需要建立不同的热平衡方程。以电池一顶角所在的点为原点建立空间坐标，轴、轴和轴的方向如图10所示。

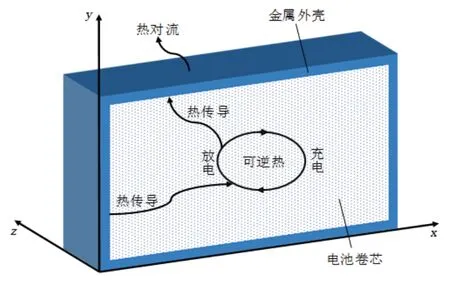
图10 电池能量传递示意图

电池产热量由电池的焦耳热、极化热及化学反应引起的熵热组成，方程为：

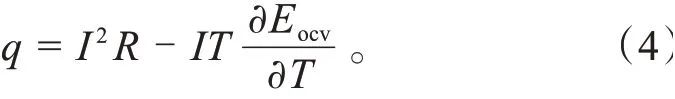
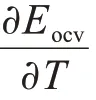
电池内部卷芯不与外界接触，因此，只考虑电池内部产热与热传导，根据能量守恒定律，建立电池内部卷芯的瞬态三维传热方程：

式中：为电池内部密度；C为电池内部比热容；λ、λ、λ分别代表电池在、、三个坐标系方向的导热系数；为电池的产热量。将、C及用一个新的参数表示，即=·C，称为热扩散率或热扩散系数，则电池内部温度计算公式为：

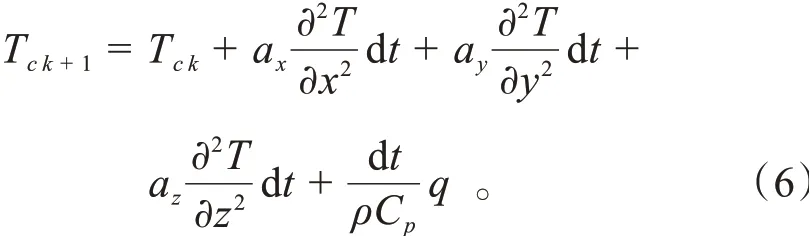
式中：T 为电池内部电芯温度预测值；T 为时刻电池内部电芯温度值；d为单位时间。

电池铝外壳与周围空气产生热量传递，并且受到来自电池内部卷芯传递的热量，电池铝外壳在轴方向的瞬态三维传热方程为：

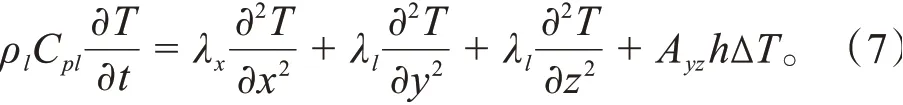
式中：ρ为电池铝外壳密度；C为电池铝外壳比热容；λ为电池在坐标系方向的导热系数；λ为电池铝外壳的导热系数；A为一个小方块的对流换热面积；为对流换热系数；∆为电池表面与周围空气的温差，将上式展开并进一步整理，可得电池外壳的温度计算公式为：

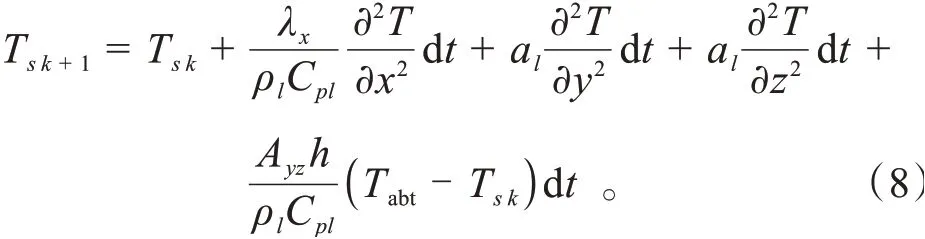
式中：T 为电池外壳温度预测值；T 为时刻电池外壳温度值；a为电池外壳的热扩散系数；为环境温度。

按照上述方法同样可求得电池金属外壳在轴与轴方向的温度计算公式。将轴、轴和轴3个方向的电芯温度与表面温度计算公式分别列出，即可获得每一时刻电池不同位置的温度。

2.2 电池温升试验

为了获取电池在大倍率充电情况下的温度状态，本文在自然对流条件下，对电池进行了1 C 及2 C 倍率的充电试验，并记录了电池在充电过程中表面的温度变化及电芯的温度变化，温升试验测试系统如图11所示。

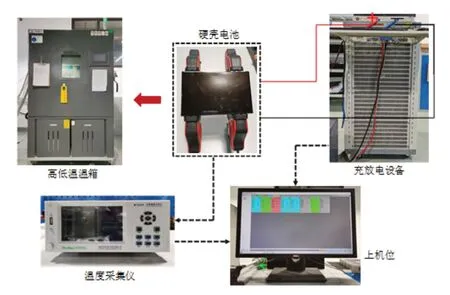
图11 温升试验测试系统

试验所测得的1 C 及2 C 倍率充电过程电池温升如图12 所示。其中，在1 C 充电过程中，先将电池恒流充电到2 000 s左右，再进行恒压充电，电池的温度先逐渐升高，到2 000 s左右时，温升速率开始快速下降，在恒压阶段，电池的温度几乎不再上升，维持在最高温度30℃左右。

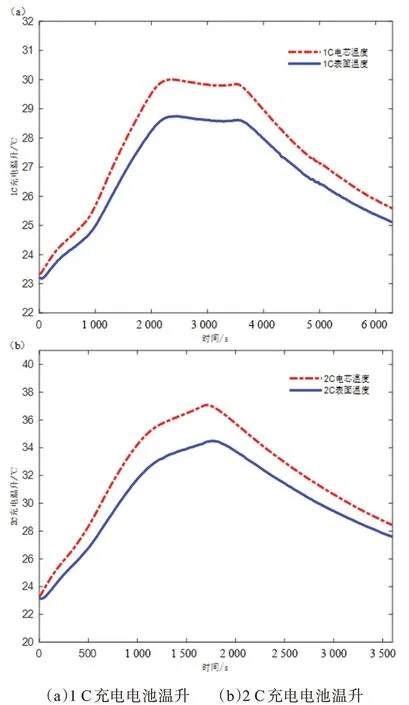
图12 电池充电温升图

试验结果表明，在自然对流条件下，1 C及2 C倍率充电时电芯温度与电池表面温度均在充电结束时达到最高。其中在1 C 充电过程中，电芯温度从23.1 ℃上升到30 ℃，表面温度从23.1 ℃上升到28.7 ℃，最大温升为6.9 ℃；在2 C充电过程中，电芯温度从23.2 ℃上升到37.1 ℃，表面温度从23.2 ℃上升到34.5 ℃，最大温升为13.9 ℃，见表4。

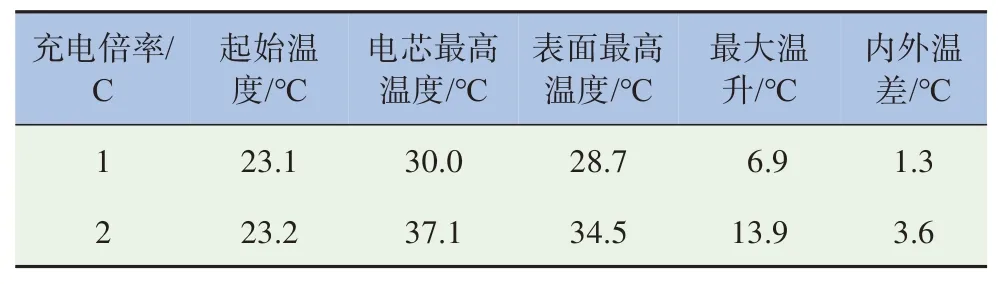
表4 1 C、2 C倍率充电电池温度变化

3 热平衡法温度预测模型结果及验证

利用有限元的思想搭建热平衡电池温度估计模型，首先将电池划分成相同的小方块，针对电池内部卷芯和电池铝外壳构建不同的热平衡方程，通过推导得到最终电池温度预测公式。本文利用所搭建的热平衡法温度估计模型，预测了1 C、2 C充电条件下电池内部各部分的温度与电池表面金属外壳温度，结果如图13所示。

图13 电池各部分温度预测结果

由模型预测结果可以看出，1 C 充电过程中电池卷芯整体温度差异不超过1 ℃，2 C 充电过程中电池卷芯整体温度差异明显，最大超过2 ℃。2 C充电过程电池卷芯与外壳温差明显小于1 C 充电，电池整体温度分布均匀。

将仿真模型所预测的电芯温度和表面温度与试验所测得的真实数据作对比，结果如图14所示。

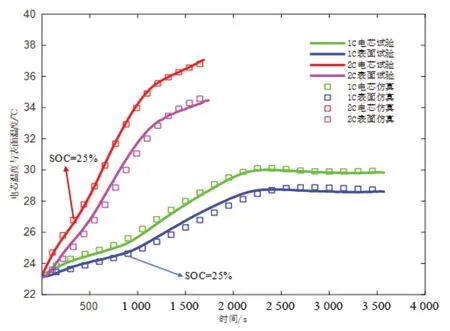
图14 热平衡法模型计算结果

从模型的计算结果可以看到，当SOC 在25%附近时，1 C 倍率充电的电池温升速率变化较明显，而2 C 倍率充电在25%SOC 附近时，电池温升速率变化幅度很小。这是因为电池在不同充电倍率下的充电热特性不同，1 C 充电时由熵变引起的热量变化是主要原因，在不同SOC 时电池熵热系数不同，引起的温升速率变化较显著，而2 C 充电时焦耳热是热量变化的主导因素，所以充电过程中电池温升速率变化不明显。

由仿真结果可知，1 C 充电所预测的电芯温度误差为0.33 ℃，表面温度误差为0.5 ℃，2 C 充电所预测的电芯温度误差为0.35 ℃，表面温度误差为0.7 ℃，见表5，模型预测最大误差不超过1 ℃，可见其预测结果准确。

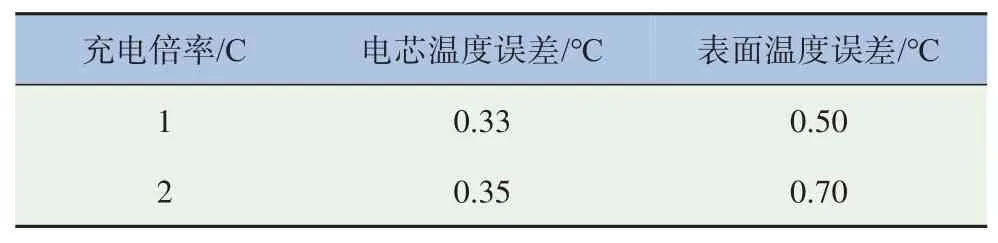
表5 热平衡法模型温度预测误差

4 结论

本文针对方形锂离子电池建立了热平衡法温度预测模型，将电池划分成等份的小块，计算出电池每一小块的温度，通过贴在电池表面和内置于电池内部的温度传感器，实现不同充电倍率下温度的测量与验证。热平衡法温度预测模型有以下优点：

（1）可以观测到电池空间温度分布细节，反映电池的温度梯度变化，所预测的电芯温度及表面温度最大误差不超过0.7 ℃，实现了电池整体温度的精确估计。

（2）合理的模型分割使热平衡法模型在5 s 内能够预测出结果，计算速度快且能够随测量温度实时预测电池温度，具有较强的实用性。

（3）针对不同倍率充电条件均可实现精确的电芯与表面温度预测，且能准确预测高倍率充电情况下的温度，对于快充条件下电池的温度预测有明显优势。