基于STEAM 教育理念下的数学建模活动教学策略与案例分析

●高照颖 赵宝江

STEAM 教育理念是集科学、技术、工程及艺术的数学跨学科教育，强调课程回归生活以学生为本，应用数学知识解决社会生产问题，推动数学学科知识与多领域知识的综合应用，在创新驱动下培养综合人才，打破传统教学中单学科教学和课堂教学中教师重理论轻实践教学的弊端，通过实践活动运用知识掌握技能提出的一种数学教学理论。

一、基于STEAM 理念的数学建模活动教学策略

STEAM 教育理念作为新教育理念，在高中建模教学的研究相对较少，数学建模活动对于高中生来说是个比较难驾驭的课题，数学建模活动提出的课题问题大多来自现实生活，解决建模活动问题需要综合物理、化学、生物、经济等领域的知识，因此教师在建模活动教学中渗透STEAM 教育理念，注重多学科的融合教学，让学生找到建模问题突破方向，经历完整建模活动，明白问题解决的来龙去脉，通过建模活动发挥主人公、决策者、合作伙伴等角色，学生是建模活动的主人公，学生亲自实践动手联系实际生活，用数学眼光观察世界，运用数学语言表达世界，让学生在建模专题实践活动中综合发展学科素养、数学建模思维，获得直接经验和实践能力，从而保证建模活动的顺利开展提出以下教学策略。

（一）精选贴近实际生活的数学建模活动课题

STEAM 理念下的教学强调实践性，数学建模活动具有开放性，因此教师和学生在共同确定探究的数学建模活动课题时，应精选贴近学生实际生活的活动课题，本着面向全体学生，活动课题的选择不应过于深奥或者理论性过强，不利于学生参与的积极性。选题应本着以学生为本，激发学生的建模活动参与的积极性，与学生现阶段的建模认知水平相契合，难度适中，学生在主动查阅资料和收集数据过程中，积累建模活动经验，真正实现在做中学数学，从而提升学生的建模思维水平。收集建模课题素材，根据现行高中数学不同版本教材整理和改编提出建模教学课题，例如，“对国民收入、消费与投资的关系的探究”“体重与脉搏探究”“决定苹果最佳出售时间点”“进货次数与总费用关系的存贮模型探究”等，或者根据现实生活提出建模问题，例如“用适当的空气隙提高暖瓶保温效能”等进行探究。

（二）建模过程中开展数学化训练

数学建模活动以实际问题背景引入，例如，“对雾霾天室内PM2.5 浓度变化探究”学生需要综合多学科查阅相关资料，对提出的实际问题转化为数学问题，再用数学知识求解。因此教师在教学中开展建模数学化训练，训练学生科学阅读能力，增强学生物理、生物、经济学等方面的生活阅历，多积累不同知识领域专有术语及相关知识，比如马尔萨斯增长模型、车流密度、放射性物质衰变、交通流量、信道容量、声音强度、投资回报率、个人所得税税率等。通过多领域科学知识的积累，帮助学生在建模活动中对实际背景的认识理解，顺利地从直观感知到抽象推理，让学生能够将实际问题抽象为数学问题并用形式化的数学语言表达出来的数学化过程。

（三）营造学生知识正迁移教学氛围

STEAM 理念下的教学强调知识迁移，在开展数学建模活动中，针对提出的课题问题，教师应创设促使学生发生知识正迁移的教学氛围，从数学模型假设、模型求解、模型的验证与反思的过程中，激发学生原有的认知对建模活动问题解决的促进作用，达到知识应用的融会贯通，真正做到学以致用。如提出建模问题“参加宴会8 人每两个人之间进行握手，共多少次握手？”教师引导学生应用原有知识多角度解决此模型问题，学生顺应思维可运用小学算法一一罗列加和；运用初中的算法平面几何求正八边形边数和对角线数；运用高中算法杨辉三角以及数列通项迭代公式算法求解等多种知识迁移应用可得共28 次。针对建模问题，综合学习过的知识，不拘泥于仅仅解决建模问题，教师应鼓励学生多途径多维度剖析问题，促使学生发生知识的正迁移，举一反三。

（四）组织建模经验交流，深化应用意识

建模活动教学中组织开展建模经验交流，师生共同进行研究成果的展示与交流，建模小组汇报本组的建模活动研究成果，汇报内容重点覆盖从收集数据到模型求解的整个过程以及出现的难点、解决方案，通过质疑、辩论、分析不足、反思，开展自我评价、同学评价与教师总结评价，总结成果并分享体会领悟。经过相互交流借鉴、取长补短，实践交流中积累数学建模活动经验，发挥小组合作能力，进一步激发学生建模活动主人公精神，学思结合形成应用数学融合多学科领域解决实际问题的意识，针对不同建模角度切入进行经验交流开拓建模视角，从而提升学生建模创新思维的发展。

二、基于STEAM 理念的数学建模活动教学案例

结合STEAM 教育理念与提出的建模活动教学策略，选取贴近高中生实际生活和符合认知规律的建模活动课题“不同包装规格商品的成本问题”进行分析。

《不同包装规格商品的成本问题》数学建模活动教学案例

（一）数学建模活动实际问题提出：

同学们，去超市购物，我们看到货物架上琳琅满目的商品（如洗衣粉、奶粉、大米、牙膏、沐浴露等）有大包装和小包装不同规格，价格也不同，那么请同学们实际调研当地便利店的商品，探究同一商品单位包装量价格与包装规格大小的关系，发现了什么？针对同一商品不同包装量与商品成本价格之间的数学关系，尝试建立数学模型并预测不同包装规格的牙膏成本价格。

（二）学生小组合作收集数据

分别统计奶粉、沐浴露、大米、牙膏不同包装规格的售价和计算单位包装量的价格，通过表格初步判断之间的逻辑关系。

（三）教师引导学生分析数据

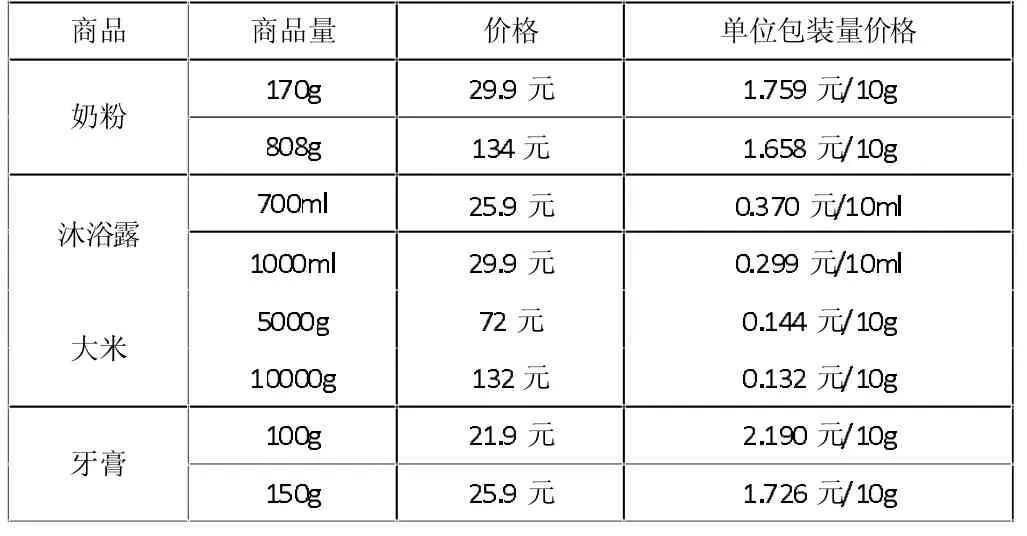
表1 不同规格商品的商品量、价格和单位包装量价格

通过表格数据统计我们可以分析得到同一商品单位包装量价格与商品包装规格的关系，即：同一商品大容量包装比小容量包装的单位包装量价格普遍少，这是由于大容量包装节省包装成本，那么我们可以进一步预测同一商品包装量（即商品量）增大时生产产品的单位成本降低，通过建立相应数学模型描述并验证我们的猜想。

（四）师生共同探究模型假设

由于商品生产过程复杂，因此要探究商品的成本价格与商品不同规格包装量的关系，将做如下前提假设：

1.商品的成本价格由生产商品的原料及加工成本和商品的包装材料及加工成本两部分组成，商品在其他生产过程中产生的成本忽略不计；

2.同一商品包装的材料是相似的，不同规格大小的商品包装外观是相似的；

3.商品包装是密合的没有空隙[1]。

根据上述生产过程的前提假设，设商品的成本价格为y元，商品的规格包装量为x（g）,商品的原料及加工成本为M1（元），商品的包装材料及加工成本为M2（元）。商品的原料及加工成本为M1（元）与商品的规格包装量成正比，包装材料及加工成本M2正比于商品的表面积S, 而包装表面积S 正比于商品体积,商品体积V 正比于商品的规格量[2]。

（五）学生小组通过数学化建立数学模型

根据上述模型假设，运用形式化的数学语言表达上述关系：

商品的生产原料加工成本：M1=kx

商品的成本价格：y=M1+M2

由此我们得到了商品成本价格与商品不同包装规格量的数学模型（2.1）。

（六）学生小组对建立的数学模型进行求解

通过调查，现有同款牙膏规格100g 成本价格为12.8 元，150g 成本价格为16.9 元，将其代入建立的数学模型（2.1），联立方程组求出参数k 和参数t，即：

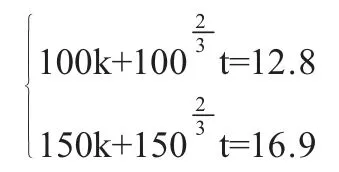
由方程组解得参数k≈0.021

从而得到该同款牙膏不同包装规格的成本价模型：

由此我们得出刻画该牙膏成本与不同包装规格量的数学模型。

（七）学生小组对建立的数学模型进行验证

根据建立的数学模型，我们预测该同款牙膏200g 的成本价格，将x=200 代入模型，解得y=21.68 元，对比调查的同款牙膏200g 成本价格21.9 元，误差值约为1%，因此我们预测的这个模型相对较成功。

（八）师生共同开展建模活动交流与总结

开展数学建模教学活动，进行建模交流活动，深化对实际问题的认识与模型的应用，通过探究“不同包装规格商品的成本问题”建立商品成本价格与商品不同包装规格量的数学模型，根据建立的模型，我们可以进一步综合分析得到：

由此可得单位商品包装量的成本（2.3）是包装规格量X的减函数，因此印证了包装规格量增加时，商品的单位包装量的成本下降。

同时，我们再进一步进行知识迁移从定性角度分析做深入研究，同一商品包装规格量增加时，商品的单位包装量的成本下降速率：

由此可得商品的单位包装量的成本下降速率（2.4）是包装规格量的减函数，因此随着商品包装规格量的增加其单位包装量的成本降低率的变化将越来越小[1]。

教师补充总结通过探究“不同包装规格商品的成本问题”建立的数学模型属于量的比例模型即轮廓模型，由两个物理量的乘幂之间的比例关系的形式表示出来，例如本探究中的包装表面积s 正比于包装体积。轮廓模型是数学建模中常用的一种模型，面对复杂的实际问题，通过简单的方式描述有关量之间的大致关系，利用量的比例关系所组建的模型就是轮廓模型[1]，是一个很实用的简化假设模型，例如“探究动物体重与心率模型”“二十一届高中应用竞赛初赛根据数据计算水库的水面面积”等实际问题对轮廓模型的广泛应用，拓宽学生的建模知识面，深化量的比例模型在不同实际问题情境中的应用。

三、基于STEAM 教育理念的教学案例反思

笔者将STEAM 教育理念与高中数学建模活动教学的有机结合，尝试探索高中数学建模活动教学新模式，选取轮廓模型进行高中建模活动案例分析，在STEAM 教育理念下应用提出的建模教学策略，使得学生在建模活动中掌握应用数学的基本技能体会数学与多学科的融合，学生在“自主”或者“合作”的建模活动方式下，提升学生数学建模抽象、归纳、演绎、类比、模拟等逻辑思维能力以及想象、直觉、顿悟灵感等非逻辑思维方法能力，培养创新驱动下综合素质人才奠定基础，通过数学建模活动综合多领域学科知识的应用，解决实际问题的创新型教学理念下的数学建模活动。