利用四阶样条快速计算信号的希尔伯特变换

覃潇潇，余 波

(三峡大学 理学院，湖北 宜昌 443002)

对任意函数f∈Lp(R),1≤p≤∞，若下述主值积分存在，则函数f在x∈R处的希尔伯特变换为

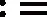
希尔伯特变换是解决数学和工程中许多问题的重要工具, 这些问题包括信号处理[1]、数值积分计算[2]、地震裂缝识别[3-5]、电气设备处理[6-7]等。有关希尔伯特变换的更多信息，请参阅文献[8]。特别地，需要通过希尔伯特变换来定义给定信号的瞬时频率，所以希尔伯特变换在信号处理领域起着至关重要的作用。Huang等[9]提出一种结合经验模态分解和希尔伯特谱分析非线性和非平稳信号的出色算法，在不同领域获得广泛关注[10]，这种方法称为希尔伯特-黄变换；后来，Chen等[11]提出一种基于B-样条的改进经验模态分解方法。此后，希尔伯特变换的计算引起了越来越多的研究兴趣。Zhou等[12]提出一种利用Haar小波计算给定函数的希尔伯特变换的方法；Micchelli 等[13]建立一种快速算法计算任何给定信号的希尔伯特变换。如果给定信号的长度为n，则计算复杂度降低到O(nlogn)，同时相比现有的方法，精度有所提高。受这项工作的启发，Bilato等[14]开发一种基于分段线性函数表示和离散三角变换(discrete trigonometric transform, DTT)计算给定信号的希尔伯特变换的算法；Abd-el-Malek等[15]提出一种基于三次样条的希尔伯特变换方法，将三次样条的希尔伯特变换表示为三次多项式和对数函数的乘积，但计算复杂度较高。如文献[14-15]所述，虽然文献[13]中方法比这2种方法的适用性更普遍，但却存在一个缺陷：不能用于逼近给定信号的样条函数在B-样条节点处的希尔伯特变换。本文旨在解决这一问题，利用四阶样条对几个常见函数计算其希尔伯特变换，并与现有方法在计算速度和计算精度2方面进行比较，说明本文算法的有效性。

本文结构如下：第1章阐述问题，描述思想；第2章给出算法；第3章介绍误差分析；第 4章展示数值结果；第 5 章是结语。

1 问题表述及思想

本章先描述如何利用四阶样条的希尔伯特变换近似计算给定函数f在有限区间上的希尔伯特变换。假设函数f在一系列点{xj:j∈Nn+10}处的值已知，其中n是要计算的给定函数f的希尔变换的点数，Nn+10={1,2,…,n+10}。称{xj:j∈Nn+10}为样本点，{f(xj):j∈Nn+10}为样本。这一设置中，假设有10个更多的样本点可用，在实际应用中，由于n往往远大于10，这一假设是可以接受的。稍后会看到这里多出来的10个样本将用于获得函数f良好的四阶样条逼近。本文主要目的是提出一种快速算法，假设样本点的间隔相等，并用h表示采样步长。在希尔伯特样条变换的一般理论中，样本点的间隔可以任意选取，感兴趣的读者可以参看文献[13]。本文目标是使用样本和四阶样条的希尔伯特变换来近似计算函数f在n个点处的希尔伯特变换值。

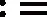
式中：[ξj,…,ξj+k]f表示函数f在节点{ξj:j∈Z}上的k阶差商；点·表示差商计算的变量。k=4的情形即为本文所讨论的四阶B-样条，也有文献称它为三次B-样条。

接下来用四阶B-样条{Bj,4:j∈Nn+6}的线性组合来逼近目标函数f，相应的B-样条节点用{ξj:j∈Nn+10}表示，即

(1)

式中cj∈R。由{cj:j∈Nn+6}组成的向量c被定义为样条函数S4的系数向量。容易看出，为了使S4很好地逼近函数f，cj应该与样本{f(xj):j∈Nn+10}有关，故令cj=λjf,j∈Nn+6。cj的具体表达式将在后文给出。

从式(1)可以看出，如果S4对目标函数f具有很好近似，那么S4的希尔伯特变换就可以用来近似计算目标函数f的希尔伯特变换。根据式(1)和希尔伯特变换的线性性质，将计算S4的希尔伯特变换问题转化为计算Bj,4的希尔伯特变换问题。由文献[8]知HR在L2(R)是等距映射，因此，将第j个k阶B-样条函数的希尔伯特变换Hj,k定义为

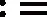
从而得到函数HRS4，在几乎处处的x∈R可表示为

(2)

下面将推导Hj,4的一般表达式。文献[11]证明对一般情况下的k，Hj,k满足de Boor递推关系，即对于x∈R，有

Hj,k+1(x)=φj,k(x)Hj,k(x)+ψj+1,k(x)Hj+1,k(x)，

(3)

式中函数φj,k和ψj,k在x∈R处被定义为

(4)

文献[13]给出了初始Hj,1，其表达式为

(5)

利用式(3)、(4)和(5)，可以得到Hj,2的一般表达式为

(6)

在Hj,2基础上，再次利用式(3)和(4)，可以得到

(7)

最终，利用式(3)、(4)和(7)，得到Hj,4的表达式为

(8)

ξj=xj,j∈Nn+10。

(9)

假设样本点是等间距选取的，因此四阶样条对应的样条节点也是等距的，这样，式(8)中的Hj,4可以简化为

(10)

式中h是采样步长。

得到Hj,4的表达式之后，回到式(1)来讨论逼近系数cj的选取。在样条逼近理论的文献中，有多种方法选取逼近系数cj，使相应样条函数对目标函数有好的逼近效果，比如插值方法、Peano核定理方法等。本文采用文献[16]中第20.4节的方法选取系数cj，即

(11)

需要强调一下，本文将利用式(2)、(9)、(10)和(11)计算四阶样条函数的希尔伯特变换，式(9)采样点与样条节点完全一致，故这种方法既可以计算采样点处的希尔伯特变换，又可以计算样条节点处的希尔伯特变换，但文献[13]中样条节点与采样点相差半个采样步长，故三阶样条方法只能计算采样点处的希尔伯特变换，而不能计算样条节点处的希尔伯特变换，这是本文与文献[13]的主要区别。根据式(2)、(9)、(10)和(11)，可以得到四阶样条的希尔伯特变换公式为

(12)

第2章将利用式(12)给出HRS4的快速算法，并用它作为目标函数f的希尔伯特变换的近似。

2 算法描述

本章主要根据式(12)来给出四阶样条的希尔伯特变换的快速算法。假设需要计算给定函数f在n个点{xl:l∈Nn}处的希尔伯特变换值，如果直接根据式(12)计算，每计算一个点的希尔伯特变换值就需要至少n+6次乘法，因此，总计算量为O(n2)。下面从矩阵角度来思考这一问题，即令

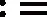
(13)

这样，A是一个n×(n+6)矩阵，u是n+6维列向量，目标则是利用快速算法来计算向量v，即希望将计算复杂度由O(n2)降低为O(nlogn)。这一目标能实现的原因在于系数矩阵A是一个Toeplitz矩阵，而Toeplitz矩阵可以填充为循环矩阵，循环矩阵与向量的乘法则可以利用快速傅里叶变换来实现[17]。

将矩阵A分成3块

A=[B1CB2]，

(14)

式中：B1和B2都是n×3矩阵，其列分别由矩阵A的前3列和后3列组成；C是一个n×n矩阵，其列由矩阵A的中间n列组成。与此同时，将向量u分为3部分

u=[p1；q；p2]T，

(15)

式中：p1∈R3和p2∈R3分别由向量u的前3个元素和后3个元素组成；q∈Rn由向量u的中间n个元素组成。因此，目标向量v可以表示为

v=B1p1+Cq+B2p2。

(16)

向量B1p1和B2p2的计算都只需要3n次乘法，所以将主要研究如何降低矩阵C与向量q的乘积Cq的计算量。为达到这一目的，首先将n×nTopelitz矩阵C填充为2n×2n的循环矩阵

式中G是一个n×n矩阵，定义如下

容易看出D是一个2n×2n循环矩阵。如果用qnew表示R2n中向量，它的前n个分量与q一致，而其余分量均为零，则向量Dqnew的前n个分量与向量Cq一致。

r=(C1,1,C2,1,…,Cn,1,0,C1,n,…,C1,2)，

(17)

通过快速傅立叶变换可以将循环矩阵D对角化，即

FDF-1=diag(Fr)。

因此，Dqnew=F-1diag(Fr)Fqnew。综上所述，可以给出计算四阶样条的希尔伯特变换HRS4的快速算法。

算法四阶样条的希尔伯特变换的快速算法

输入：已知样本点{xj:j∈Nn+10}和采样{f(xj):j∈Nn+10}。

输出：给定样本中间n个点处的希尔伯特变换值{HRS4(xl):l∈Nn}。

1)根据式(9)和(11)，得到 {ξj:j∈Nn+10}和 {cj:j∈Nn+6}。通过式(10)，计算矩阵A的第1行和第1列元素。

2)由矩阵A的第1行和第1列的元素生成整个矩阵A。矩阵B和矩阵C由式(14)得到，向量p和q由式(15)得到。

3)计算式(16)右边的第1个和第3个向量，用ω1和ω2表示，即ω1=B1p1,ω2=B2p2。

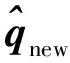
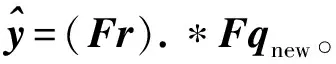
由该算法可以得知，第3)步的乘法计算量为3n+3n=6n；第4)步和第5)步中用到快速傅里叶变换，计算复杂度为O(nlogn)；第6)步中用到2个向量的对应分量乘法，计算量为2n。其他步骤中的计算量足够小，可以忽略。综上所述，本算法的计算复杂度为O(nlogn)。

3 误差分析

本章将给出利用四阶样条近似计算给定函数f的希尔伯特变换算法的误差估计。

在文献[13]中，k阶样条的希尔伯特变换对目标函数f的希尔伯特变换的逼近误差为

(18)

引理1如果f是3次多项式，那么对于所有xj,j∈Z，有S4(xj)=f(xj)，S′4(xj)=f′(xj)，S″4(xj)=f″(xj)。因此，S4=f。

证明根据式(1)和(11)，对任意j∈Z，有

引理2如果f∈C4(R)，J是非空有界闭区间，则有

证明任取t∈J, 并在ξ∈R上定义3次多项式g为

由引理1，得

式中λl(g-f)为f(t)-S4(t)的样条逼近系数。由于所有Bl,4(t)非负且小于1，

代入四阶样条的样条系数，得

根据文献[16]中定理20.4，得

由B-样条的性质，Bl,4(t),l∈Nn+6在t处最多有3个非零的B-样条节点。因此，当Bl,4(t)≠0时，可以确定

|xl+1-t|≤h，|xl+2-t|≤2h，|xl+3-t|≤3h。

式中r是某个正整数。在不等式(18)中取k=4，并利用引理2，可得定理1。

4 数值实验

本章将给出一些数值结果，证明本文所提方法具有更好的计算精度和更快的计算速度。下面选择表1中4个函数进行数值实验，选取这些函数的原因是它们的希尔伯特变换具有解析表达式。

表1 4种函数及它们的希尔伯特变换

本文数值实验在配置为Intel i7-4790、3.60 GHz 处理器、16 GiB RAM和操作系统为 Microsoft Windows 7的个人计算机中使用MATLAB(R2014A)完成。将所提四阶样条方法(四阶HST)与大多数现有计算给定函数的希尔伯特变换的方法进行比较，即 FFT方法[18]、Haar小波方法[12]、离散三角变换方法(DTT)[14]和文献[13]中所涉及的三阶样条方法(三阶HST)。从计算精度和计算速度两方面比较这些方法的数值性能。为此，在L2范数下，定义函数的希尔伯特变换HRf与样本点{xj:j∈Nn}处的计算结果u之间的相对误差为

类似地，在L∞范数下，两者之间的绝对误差定义为

然后记录这5种方法的L2范数相对误差E2和L∞范数绝对误差E∞，并在表2到表9中列出。为了评估不同方法的计算效率，还记录了每种方法的计算时间。将样本点作为自变量，L2范数相对误差E2和计算时间乘积的对数函数值作为因变量，然后在同一窗口中用曲线表现两者的关系。如图 1、图 2、图 3和图 4所示。

表2 在区间[-10,10]上函数希尔伯特变换的L2范数相对误差

表3 在区间[-10,10]上函数希尔伯特变换的L∞范数绝对误差

表4 在区间[-5,5]上函数希尔伯特变换的L2范数相对误差

表5 在区间[-5,5]上函数希尔伯特变换的L∞范数绝对误差

表6 在区间[-5,10]上函数希尔伯特变换的L2范数相对误差

表7 在区间[-5,10]上函数希尔伯特变换的L∞范数绝对误差

表8 在区间[-10,5]上函数希尔伯特变换的L2范数相对误差

表9 在区间[-10,5]上函数希尔伯特变换的L∞范数绝对误差

图1 5种计算函数的希尔伯特变换方法比较

图2 5种计算函数希尔伯特变换方法比较

图3 5种计算函数的希尔伯特变换方法比较

图4 5种计算函数的希尔伯特变换方法比较

从表2～表9中可以看出，在L2范数相对误差E2和L∞范数绝对误差E∞的数据中，三阶样条方法和四阶样条方法的误差均小于其他3种方法，其中Haar小波方法和DTT方法的误差都小于FFT的误差，因为Haar小波方法中利用到伸缩因子，DTT方法涉及到离散三角变换，所以在误差上它们都优于FFT方法，但计算时间比FFT方法长。通过图1～图4可以看出，如果考虑计算时间，那么三阶样条方法和四阶样条方法在计算精度和计算速度上都优于其他3种方法，因此二者都具有较好的逼近性能。在第4个函数中，四阶样条方法得到的L2范数相对误差E2和L∞范数绝对误差E∞均分别优于三阶样条方法，而在前3个函数中，虽然四阶样条方法得到的L2范数相对误差E2优于三阶样条方法，但三阶样条方法得到的L∞范数绝对误差E∞仍优于四阶样条方法，产生这个现象的原因可能是cj的选取不好，从而导致L∞范数绝对误差不优于三阶样条方法。根据这一现象，后续工作将进一步研究样条系数cj更好的选取方式。

5 结语

本文给出用四阶样条近似计算目标函数的希尔伯特变换的快速计算方法，在计算过程中直接使用样本点作为四阶样条节点，解决了文献[14-15]指出的希尔伯特样条变换方法不能计算目标函数在样条节点处的希尔伯特变换的问题。然后给出利用四阶样条近似计算目标函数的希尔伯特变换的计算复杂度和误差估计。数值结果表明：本文算法在计算精度和速度上都具有很好的性能。未来工作将进一步研究样条函数特点，设计更好的快速算法，达到好的逼近性能。