两个移动荷载作用下简支梁的动力耦合分析

石红迁SHⅠHong-qian

（广东盛翔交通工程检测有限公司，广州 511400）

0 引言

随着科技的不断进步，交通运输系统也在不断发展完善。在各种运输系统（如公路、铁路）中，车辆行驶速度越来越快、车流密度不断增加，车辆与桥梁的动力耦合现象也引起了人们的重视[1，2]。一方面，车辆在桥梁上的快速运动，会对桥梁造成动态的作用进而引起桥梁的振动，对桥梁的工作状态与其使用寿命造成一定的影响；另一方面，桥梁的振动也会对桥上行驶的车辆产生相应的作用，进而威胁到车辆行驶的稳定性与安全性[3，4]。因此，研究车-桥动力耦合问题，对车辆与桥梁在动态过程中的状态进行分析与研究，可以为需要承担动态车辆荷载的桥梁的设计提供一定的理论依据与实践指导。相对于传统等截面梁桥来说，变截面梁桥具有受力合理、节省材料等优点，应用到了越来越广泛的工程实践中[5]。因此研究变截面桥梁与车辆的动力耦合问题有着重要意义。

本文对指数变宽度矩形梁模型在两端简支条件下，受到一前一后两个同向移动常荷载作用时的动力响应进行了相关的分析研究。采用模态迭加法进行分析，通过推导得到了问题的理论解。并在理论解的基础上，详细研究分析了非均匀系数与速度两项参数对振动响应的影响。其结果可以为相关桥梁工程设计提供相关的理论依据与一定的实践指导。

1 两端简支变截面梁的动力响应

1.1 问题简述

针对实际中在简支梁上车辆行驶时桥梁的振动响应问题，本文建立了一个两端简支矩形梁在受到两个同向移动常荷载作用下的动力耦合模型，如图1 所示。其中，假设梁的截面是非均匀的，其变宽度函数为b（x）=b0eax，且b0为初始宽度，梁横截面的高为常数。

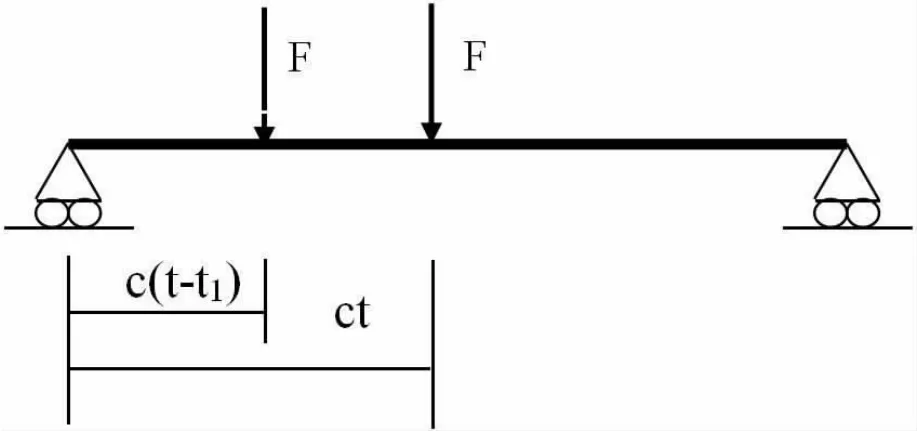
图1 两载荷同向移动模型示意图

在梁上作用有两个同向动态常荷载，模拟桥梁车辆行驶。两荷载一前一后，我们认为这两个力是同时同地出发的，只是在最初的t1时间段内第一个力恒定的速度出发，而第二个力的速度为0，在t1时间过后，第二个力才获得速度开始移动。

1.2 理论解推导

模型动力学方程形式如下：

式中，E0、I0为初始截面的弹性模量与惯性矩，ρ0和A0为初始截面密度与截面积，K（x）为截面惯性矩的变化函数，m（x）为截面面积的变化函数，v（x，t）为梁变形函数，F为所施加的力的大小，δ（x）是脉冲函数。

式（1）可以写为以下两式的和

记

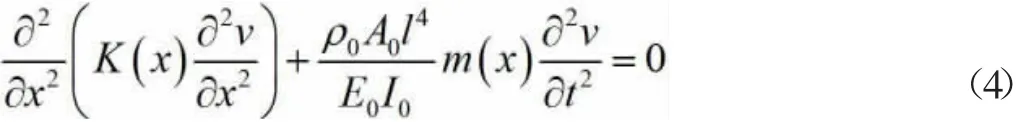
化简得

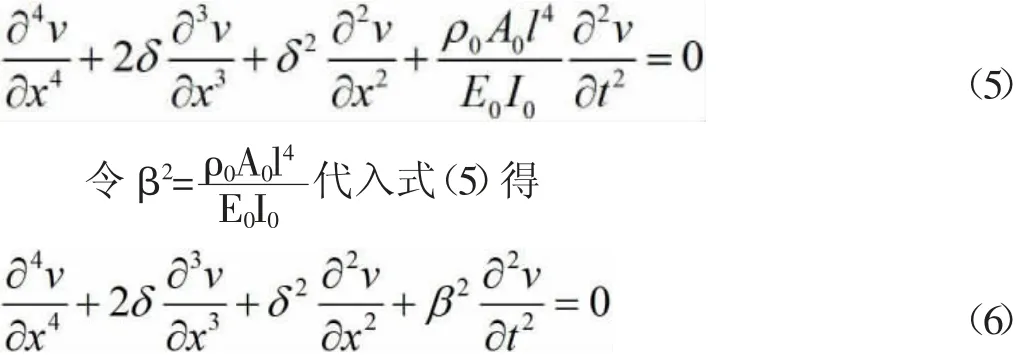
令v（x，t）=ΣVi（x）·qi（t）代入式（6）中可得

解为

进一步求解qi（t）：

令v（x，t）=Σi=1Vi（x）·qi（t）代入式（2）中可得

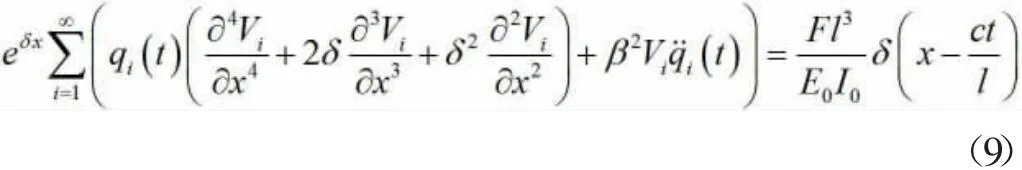
对（9）从0 到1 进行积分

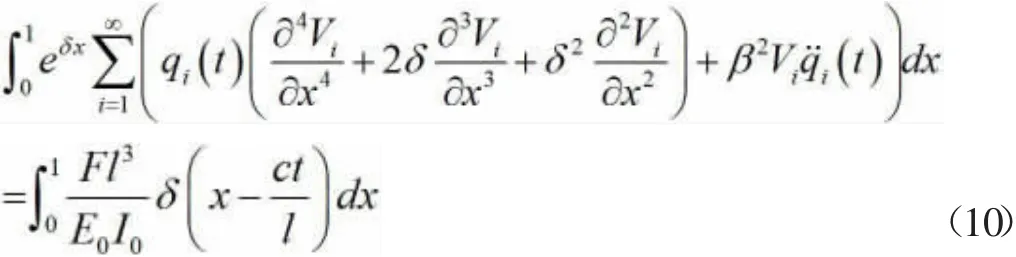
方程式（10）两边同时乘以Vi可以得

对于两边简支问题有：

则式（11）化简为

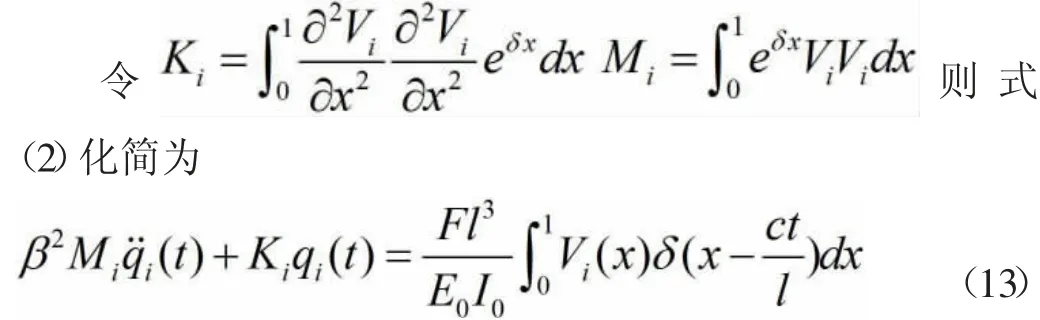
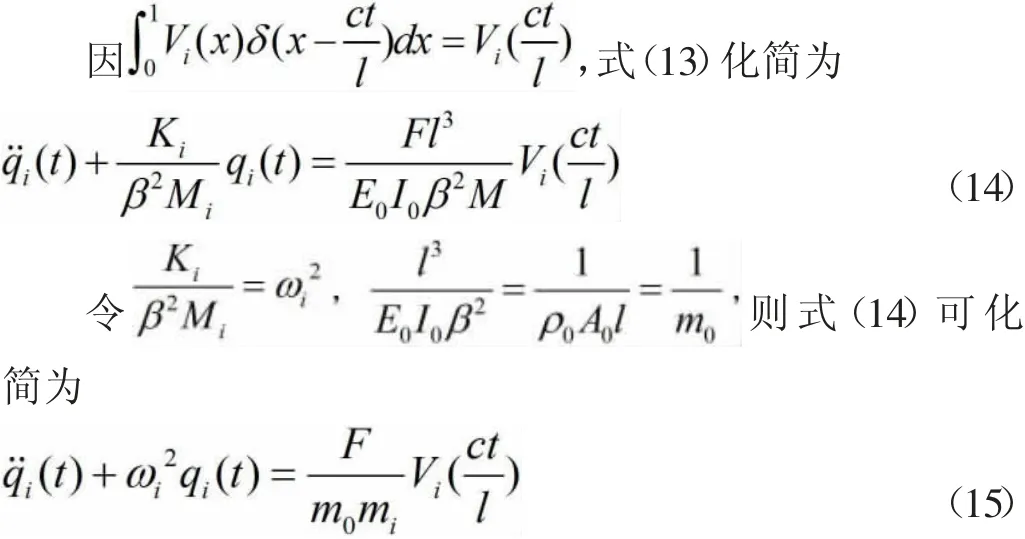
同理式（3）可转化为

对式（15）利用杜哈梅积分公式得

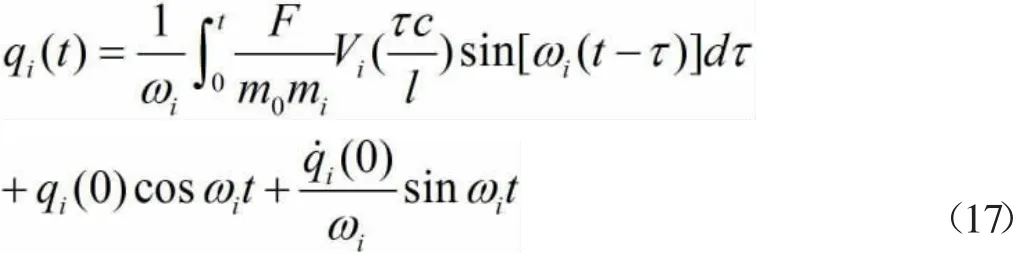
故式（17）化简为

同样对式（16）利用杜哈梅积分公式，并化简可得

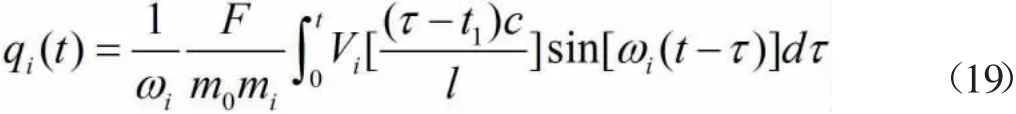
通过进一步的推导我们可以得到

其中

进而我们可以得到两端简支情况下

2 相关参数对动力响应的影响

2.1 非均匀系数δ 对移动荷载响应的影响

应的七条曲线，如图2 所示。

图2 不同非均匀系数对简支梁振动响应的影响

上图说明，随着δ 由小变大，相应的跨中处的挠度逐渐减小，图示不仅给出了定性的趋势，而且给出了定量的数值。出现这种现象是由于δ 的逐渐增大引起a 的逐渐增大，使得桥梁的宽度的变化量不断增加进而使得桥梁的重量增加，相应的移动荷载对桥梁的影响就会减小。

2.2 速度对移动荷载响应的影响

众所周知，桥梁的动力响应与移动荷载的移动速率有密切的联系，荷载的移动速度达到特定的区间时，还会使桥梁产生共振。而当速度达到一定大小时，桥梁的最大响应将会出现在移动荷载过桥之后。我们通过改变不同的速度值，来分析研究荷载移动速度对本桥梁模型的影响是否符合现实情况。

为使速度有较大的变化范围，我们取速度从0.1m/s到30m/s 进行画图，如图3 所示。

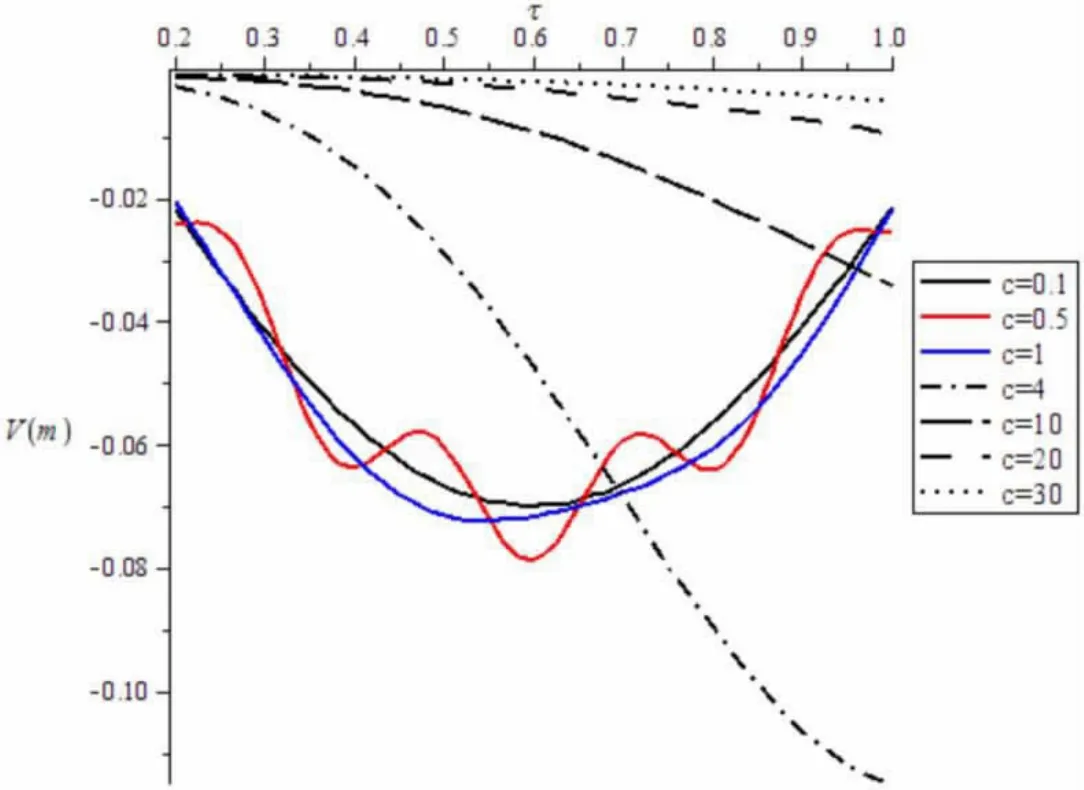
图3 不同移动速度对简支梁振动响应的影响

从上图我们发现当荷载移动速度为4m/s 附近时，跨中挠度达到最大；而当速度超过10m/s 时，跨中挠度的最大值出现在移动荷载离开的瞬间。

3 结论

本文建立了简支变截面梁与两个同向移动常荷载的动力耦合模型，验证了理论解的准确性，并对相关参数进行分析研究，其结果对指导变截面梁桥的设计与应用存在一定的理论意义与实践价值。主要结论如下：

①通过模态叠加法推导得到问题的理论解，并将理论解与Maple 数值计算结果进行了比较，二者吻合较好。

②本文深入分析了非均匀系数对振动响应的影响，通过分析相关图中的结果，我们发现随着变截面梁桥非均匀系数的增大，其跨中的挠度将不断减小。这是因为非均匀系数的增大，桥梁的宽度将不断增大，进而造成桥梁的重量不断增加，移动荷载对桥梁的影响将不断减小。

③移动荷载对桥梁的影响与移动荷载的移动速度有着密切的关系，为了进一步了解移动荷载速度与桥梁对移动荷载的动力响应之间的关系，本文对荷载移动速度进行了分析研究。结果表明，当移动荷载的速度达到4m/s 附近时，跨中的挠度将达到最大；当荷载移动速度超过10m/s时，跨中挠度将在移动荷载离开的瞬间达到最大值。这与现实情况有较好的一致性。