基于改进DPC和特征分区的点云去噪算法
耿 蜜,朱 攀,周兴林
(1.武汉科技大学 冶金装备及其控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学 机械传动与制造工程湖北省重点实验室,湖北 武汉 430081)
1 引 言
随着三维激光扫描技术的发展完善及各种扫描设备的日益普及,三维点云已经成为一种常见的空间三维物体的表示信号。三维激光扫描因其测量精度高、数据获取快、适用场合多等诸多优势被广泛应用于地形勘测、文物保护、计算机视觉、无人驾驶等各个领域[1-3],通过对扫描仪采集到的物体表面信息点云进行逆向建模从而实现物体复现。然而受限于仪器精度、被测物件复杂度、环境干扰、人为操作误差等因素,获取的点云数据通常包含着部分噪声,这些噪声将严重影响后续的数据处理工作,因此点云去噪工作成为了点云逆向建模中不可或缺的一环。
点云去噪在近年来一直是一个备受国内外学者关注的研究课题,去噪算法也是种类繁多,各有所长:Fleishman[4]等将图像双边滤波引入点云去噪,通过使用局部邻域信息对点进行沿法矢方向的偏移实现了光顺效果,但无法处理较大误差的离群点且易造成过光顺。Mattei[5]等受图像稀疏去噪启发,通过加权L1最小化点偏离局部参考平面从而保持点云尖锐特征,去噪性能优异但在高噪声下计算量显著增大且法矢方向可能出现错误。Rakotosaona[6]等提出一种基于深度学习的PCN去噪框架,该框架无需预先设置参数,通过去除离群点并对剩余点修正达到去噪效果,但相应地需要成对的干净噪声训练数据,且噪声特性与训练数据不同时效果较差。Zeng[7]等利用曲面块的自相似性,引入低维流形模型并通过图维拉普拉斯正则化最小化流形维数达到去噪效果,但计算复杂度较高。Zhou[8]等提出一种非迭代双阈值去噪方法,对点云进行分层处理,去噪速度快且鲁棒性强,但特征保持度欠佳。王晓辉[9]等通过点到拟合平面的法向距离对点进行划分,并分别采用加权局部最优投影和双边滤波对不同区域点去噪,改善点云分布均匀性的同时保持了尖锐特征。柳赟[10]等基于主成分分析与曲面拟合原理,通过法矢粗去噪后进行曲面拟合,再根据点到拟合曲面距离精去噪,对于平坦区域具有较好的去噪效果。赵夫群[11]等采用层次化的去噪方案,首先基于张量投票完成点云初始去噪,然后通过设置曲率阈值剔除异常点实现精细去噪,该算法复杂度较低,执行效率高。魏硕[12]等通过kd树求取点云密度并设置阈值粗去噪,然后融合改进DBSCAN和统计滤波对数据进行精细去噪,性能优于传统的半径滤波且参数自适应能力强。
从近年来点云去噪方法的发展趋势不难看出,单种去噪方法难以满足复杂的去噪环境需求,融合型去噪方案更具普适性,因此本文提出了一种综合性的去噪方案,通过对点云噪声进行分尺度、分区域地去除,从而实现对包含混合噪声的点云数据的适应性。
2 算法描述
本文首先通过改进的密度峰值聚类去除大尺度噪声,得到粗去噪数据后根据点的曲率等信息进行特征判断分区,对不同区域的点云采取相应的去噪算法,具体的去噪流程如图1所示。
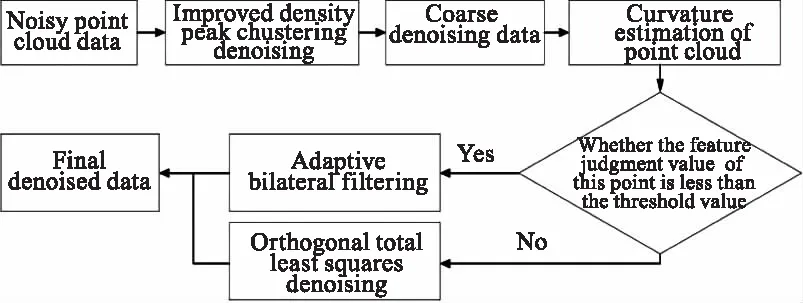
图1 去噪算法流程图Fig.1 Denoising algorithm flow chart
2.1 密度峰值聚类算法相关概念
2.1.1局部密度ρi
局部密度是指点pi在以dc为半径的圆内的邻域点个数,即:
(1)
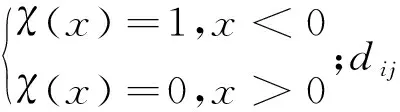
2.1.2 最邻高密度点距离δi
该距离为点pi与局部密度大于它的点的最小距离,即:
(2)
2.1.3 两个假设
DPC(Clustering by fast search and find of density peaks)算法[13]认为:聚类中心周围的邻域点的局部密度较小;聚类中心与局部密度较大的点的距离较远。
2.1.4 改进的DPC算法
DPC算法基于欧氏距离及密度对数据进行分类,不仅可以完成任意形状任意维数数据的聚类,同时能够发现并剔除异常点,但需要计算任意两点间距离,计算开销较大,且聚类中心需要通过观察pi及δi的决策图进行人工选取,提高了算法的冗余度。
为了克服DPC算法的不足,本文对数据进行分组降低数据量从而提高运行效率,在此基础上引入文献[14]中簇中心权值γi,从而实现簇中心点的自动选取。
改进后的DPC去噪具体步骤如下:
(1)首先对原始点云数据进行分组,根据样本数N确定分组数n,由表1可以得出:为保证最佳运行效率,n取[N/1000],然后对分组后各组数据进行步骤(2)~(6)处理。

表1 不同分组数下DPC算法运行时间Tab.1 Running time of DPC algorithm under different number of packets
(2).计算各点间距离并作升序排列,截断距离dc取前2%处数值并计算各点的ρi和δi。
(3).对ρi和δi作降序排列,根据噪声高低设置噪点判断阈值s,将δi位于前s%且ρi位于后s%的点标记为噪点。对bunny点云添加信噪比RSN为10 dB的随机噪声并在不同s值下利用改进的DPC进行去噪,结果如图2所示,可以看出:当s为95时,仍残留着部分噪声点;而当s=75时,部分边缘也被当作噪声去除;s=85时去噪效果较好。因此通常情况下s取值应略小于(100-RSN)。


图2 阈值s取不同值下DPC算法粗去噪效果Fig.2 Coarse denoising effect of DPC algorithm with different threshold s
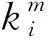

(5)将剩余各点分配到距离它最近的局部密度比它高的点所属的簇。
(6)各点分配完成后对各簇包含点数进行判断,设定阈值nmin,通常取nmin为25~30,将点数量小于nmin的簇标记为群聚噪点。
(7)去除各组标记噪点后合并数据,得到粗去噪数据。
2.2 点云法矢及曲率估算
在对原始点云数据进行大尺度去噪后,我们需要进一步去除距离点云主体较近的小尺度噪声,然而这些噪点难以仅仅通过点的三维坐标信息进行区分,因此需要通过估算点的法矢及曲率作为点的信息补充。
2.2.1 点云法矢估算
本文采用常用的主成元分析法(PCA)进行法矢估计,给定粗去噪后的点集P={pi,i∈1,2,…,n},pi∈R3中的点pi及其k邻域N(pi)={pj,j∈1,2,…,k},pj∈P,得到点pi的协方差矩阵C(pi):
(3)

2.2.2 法矢方向调整
通常情况下由PCA得到的点的法矢会零散地指向点云主体的不同侧,这会严重影响后续去噪的准确性,因此需要对法矢方向进行一致性调整。而目前常用的最小生成树法效率低下,难以应用于数据量较大的点云数据,因此本文提出一种基于邻域传播的法矢修正法,相较于传统的最小树生成法,降低了调整时的搜索范围且逐步增加传播点个数,极大地提高了法矢调整的效率,主要流程如图3所示。
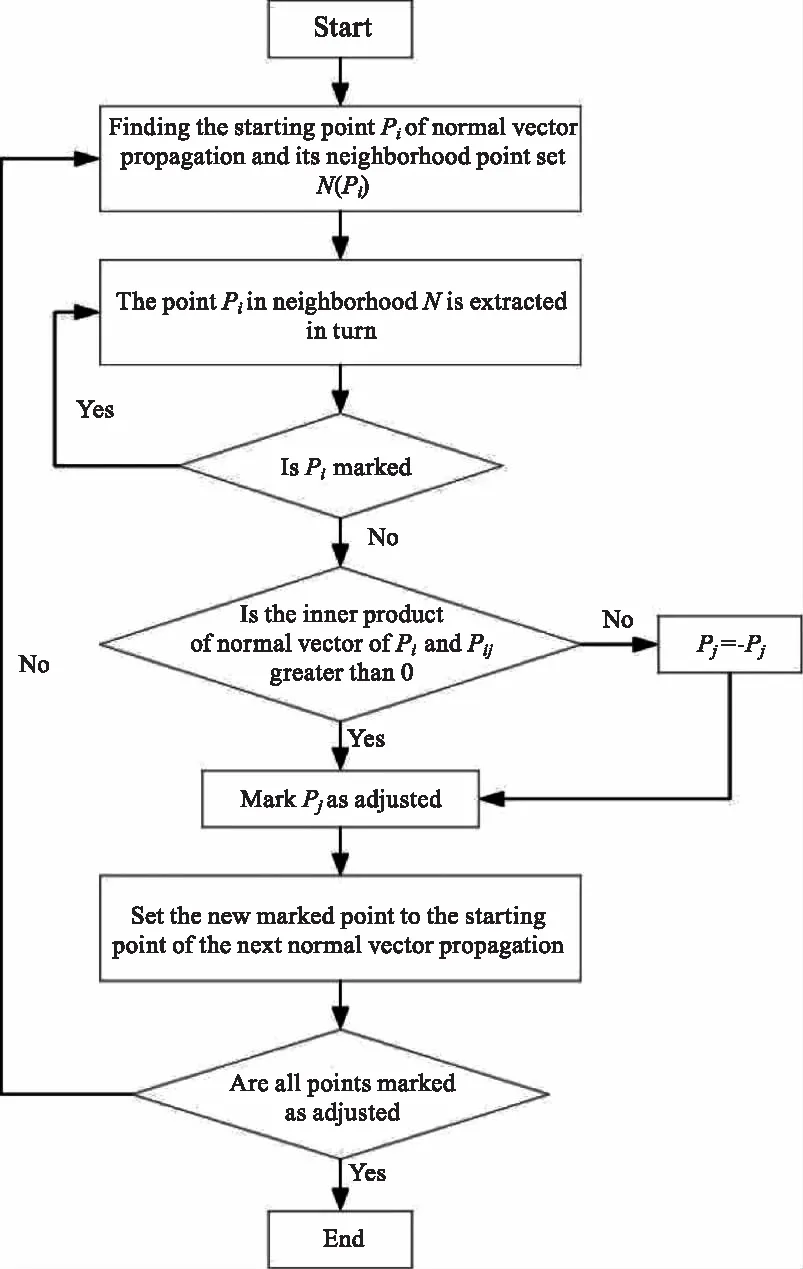
图3 法矢方向一致性调整流程图Fig.3 Flow chart of normal vector direction consistency adjustment
首先选取法矢传播起始点,这里选取z轴坐标最大的点作为起始点,依据其法向量n与[0,0,1]的内积大于0进行方向调整;确定起始点后按照上图流程依次对其邻域各点法矢进行调整,调整基于相邻点法矢夹角小于90°这一规则进行,至此完成一次调整循环,随后更新法矢传播点,再次循环直到所有点调整完毕。
2.2.3 点云曲率估算
由特征矩阵C得到的特征值λ1代表着法矢α1的偏移量,即数据点相对其切平面的偏移程度,因此引入曲面变分[15]r近似代替曲率R来表征局部区域的几何特征,其表达式为:
(4)
2.3 小尺度噪声去除
为了在保证特征信息损失较小的前提下去除小尺度噪声,需要对点云进行特征判断分区,对不同区域点云采用不同的去噪算法以达到最佳去噪效果。
本文基于点曲率及其标准差对点云进行特征划分,已知点pi的曲率为Ri,其邻域内的平均曲率为:
邻域点曲率标准差为:
则定义特征判断值e:
(5)
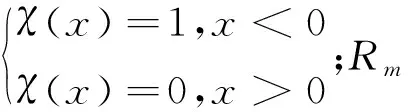
2.3.1 平坦区域噪声去除
针对平坦区域点云,使用基于平面拟合的去噪方法较为合适,通过计算各点到拟合平面距离并设定阈值剔除噪声。因此选择兼顾自变量与因变量误差的正交整体最小二乘法[16]进行平面拟合,具体步骤如下:
(1)建立拟合平面模型

(6)

(2)由式(3)的协方差矩阵C特征分解求得的特征值λ1对应的特征向量α1即为a,b,c的值。
(3)计算点到拟合平面距离di
(7)
(4)根据仪器精度ε设置距离阈值dmax,当di>dmax时,将该点作为噪点删除,反之保留。
2.3.2 特征区域噪声修正
在特征区域,选择特征保持效果较好的双边滤波[4]并加以改进,通过为高斯滤波参数添加特征权实现参数自适应选择。该方法利用点邻域信息对数据点云进行法矢方向的移动从而修正点坐标位置达到光顺效果,在双边滤波中:
p′=p+α·n
(8)
其中,α为双边滤波因子;根据α及法矢n对原始坐标p进行调整得到新的坐标p′,α的计算公式如下:
(9)
(10)
(11)
其中,k为采样点p邻域中点个数;pi为邻域点;ωc,ωs分别为光顺滤波权函数和特征保持权函数,控制两个函数大小的参数σc和σs分别对应着双边滤波的光顺程度和特征保持度,通常情况下,σc取邻域半径:
σc=max‖p-pi‖
(12)
当σc确定后,σs的取值对平滑效果影响较大,σs越大,代表p的法向修正距离越大,平滑程度越大,因此令:
σs=t·σc
(13)
(14)

3 实验及结果分析
本文选取特征丰富的bunny点云和以平面为主的block点云进行去噪实验,并将实验结果与通过正交整体最小二乘法和双边滤波去噪后的效果进行对比。图4、5分别为bunny和block两个点云模型在不同算法下的去噪效果图。对于特征较多的bunny点云模型,从图4(b)可以看出,仅采用正交整体最小二乘法去噪后虽然整体平滑程度提高,但特征细节损失较为严重,在图4(c)中,仅使用双边滤波去噪后,光顺度有一定程度提高,特征保持效果也较好,但无法去除远离主体的大尺度噪声且噪声污染严重区域整体光顺度较差,而图4(d)中采用本文算法去噪后,可以看到模型整体无明显噪声,模型表面轮廓特征清晰,光顺度也较好。对以平面为主的block点云模型,图5(b)中,仅采用正交整体最小二乘法去噪后,光顺效果好,仅在边缘尖锐处有部分损失,图5(c)中双边滤波去噪同样无法去除大尺度噪声,且光顺效果较差,图5(d)中本文算法去噪后,模型光顺效果较好且尖锐特征得到保留,仅在噪声污染严重处有小幅波纹。


图4 不同去噪算法下bunny点云去噪重构模型效果对比图Fig.4 Comparison of the rabbit point cloud denoising reconstruction model under different denoising algorithms


图5 不同去噪算法下block点云去噪重构模型效果对比图Fig.5 Comparison of the block point cloud denoising reconstruction model under different denoising algorithms
综合图4、5的结果对比可以看出,正交整体最小二乘法对于平面光顺效果较好,但特征保持不佳,双边滤波则受大尺度噪声影响较大,而本文算法能够同时处理大小尺度噪声,针对各类点云模型均能兼顾光顺及特征保持效果,具有良好的适应性。
为了进一步衡量本文算法的去噪性能,还需要引入多种定量评价指标验证算法的可行性。点的坐标误差可以直接反映去噪效果的好坏,而在特征保持度上,本文引入信息熵[17]作为评判标准,点的信息熵取决于所在区域的无序程度,因此可以用于描述点的特征丰富度。去噪时间则决定着算法的运行效率,因此本文通过最大误差、平均误差、点平均信息熵、去噪时间这四个评价指标来对去噪结果进行更加客观的分析。平均信息熵的计算公式为:
(15)
(16)
(17)
(18)

不同去噪算法下计算结果如表2所示。

表2 不同去噪算法客观评价对比Tab.2 Objective evaluation and comparison of different denoising algorithms
从表2可以看出,本文算法对两组点云去噪后的最大误差与平均误差均小于另两种算法,即整体去噪效果优于另外二者。在平均信息熵上,对于特征丰富的bunny点云,本文算法去噪后的结果高于另外两种算法,说明特征信息保留越完整;对于以平面为主的block点云,本文算法去噪结果低于另外二者,说明整体光顺效果越佳。而在去噪时间上,由于本文算法步骤较多,参数需要自适应调整,因此运行时间较另外二者有所增加,但运行效率基本能够满足日常需求。
为了验证本文算法的可行性,通过对block点云添加不同强度的高斯噪声并使用本文算法进行去噪,结果如图6所示。


图6 不同强度高斯噪声下本文算法去噪效果Fig.6 Denoising effect of the algorithm of this paper under different intensities of Gaussian noise
由图6可以看出,本文算法在面对不同强度的噪声时均能取得较好的光顺效果,结合前面的去噪性能对比可以得出,本文算法整体优于单独使用正交整体最小二乘法和双边滤波,且具有良好的适用性。
4 结 论
针对三维点云数据后处理过程中的去噪问题,本文提出了一种融合型算法,首先通过改进的DPC去除远离点云主体的大尺度噪声,减小了后续点云k邻域及法矢、曲率等信息估算的误差,同时基于邻域传播的法矢方向调整方案使得法矢方向调整时间大大缩短。在对点云进行特征分区后,对不同区域点云分别采用适用于平面的正交整体最小二乘法和倾向于保留特征的改进的双边滤波进行去噪以到达最佳效果。从实验结果可以看出:本文算法在面对不同点云模型与不同强度噪声时,均能得到较好的去噪效果,具有一定的的普适性,且去噪性能相较于单独使用正交整体最小二乘法或双边滤波均有一定的提升。后续工作中如何提高算法运行效率将是下一步工作的重点。

