一种基于不连续伽辽金方法求解多区域目标散射问题的优化预处理器

张慧雯 黄晓伟 吴比翼 盛新庆

（北京理工大学信息与电子学院应用电磁研究所，北京 100081）

引 言

在电磁计算应用中，由介质和金属结合的多区域结构有着广泛的应用价值.典型的介质金属结合的多区域目标，例如天线-天线罩系统、微波天线阵列等，无法通过建立单一等效模型得到准确的电磁计算结果. 而一些曾经使用单一区域模型来计算电磁特性的目标，也可以通过细化区域结构的方式得到更精确的结果，比如飞行器、导弹模型等. 因此，研究多区域目标的高效、高精度电磁计算方法是十分必要的.

为了提高多区域目标的电磁计算效率，我们使用面积分(surface integral equation, SIE)[1]矩量法(method of moment, MoM)[2]以更高效地求解分块均匀目标的散射问题，因为其相较于体积分方程具有更少的未知数. SIE 方程一般使用Rao-Wilton-Glisson(RWG)基函数进行离散[3]，但RWG 基函数的连续性使得其很难处理多区域目标的区域结合边界[4]. 通常的解决方法是在边界处增加区域连接模型(connectregion modeling, CRM)以保证边界的连续性条件，但这需要共型区域剖分[5]. 然而当目标具有精细几何结构时，共型剖分是十分繁琐且耗费时间的[6-7].

为解决上述问题，区域分解技术(domain decomposition method, DDM)被前人提出，以在不同区域中使用非共型且相互独立的几何剖分[8]SIE 方程的区域分解可以分为两大类：封闭式区域分解(体分解) (volume-based SIE-DDM)和非封闭式区域分解(面分解)(surface-based SIE-DDM)[9]. 封闭式区域分解以体积为基本区域单元，在子区域的连接处需要施加Robin传输条件(TCs)以保证子区域电流的连续性[10-11]，而这将带来更多的未知数. 非封闭式区域分解方法中，不连续伽辽金 (discontinuous Galerkin, DG)方法的研究最为深入[12-13]. 在不同面区域的边界处，DG 方法使用半RWG 基函数进行剖分，同时将电流的连续性条件直接加在半RWG 的阻抗矩阵元素上. DG 方法无需增加未知数，因此该方法的非共型剖分可以更容易地运用在复杂目标中. 近年来，学者已将DG 方法成功运用于完美电导体[14-15]、均匀介质[16]和阻抗边界表面[17-18]等目标的计算中，而对于多区域结构的目标，该方法还未有深入的研究.

对于电大目标的仿真，预处理技术是一种加速迭代收敛的有效方法[19-20]. 近场预处理器(near-field preconditioner, NFP)是多层快速多极子方法(multilevel fast multipole algorithm, MLFMA)[21]常用的预处理方式. 对于复杂的多区域目标，其近场矩阵元素非常多，增加了预处理矩阵求逆的运算时间. 距离稀疏预处理器(distance sparse preconditioner,DSP)使用距离限制减少了预处理器的矩阵元素，可以明显减少计算时间和内存需求[22]. 进一步，我们提出了优化距离稀疏预处理器(optimized DSP, ODSP)，不同积分算子的矩阵块，其数值大小随距离变化的趋势不尽相同. 算子的预处理矩阵块可以保留更少的矩阵元素而并不会大程度削弱其预处理的效果. 对于多区域目标，O-DSP 对不同的子区域矩阵块使用不同的构建方法，使之合成为完整的预处理矩阵. 与DSP 相比，O-DSP 保持了相近的加速收敛效果，而且构建的预处理矩阵元素数目大幅降低.

1 理论与公式

1.1 多区域目标的电磁散射计算

考虑图1 所示的交界面模型，这里 Ωi表示不同的体积区域，可以是均匀介质或金属. 金属 δi=0，均匀介质 δi=1. 任意两个空间区域的交界面用S ij表示，默认法相方向nˆij以区分面的外表面和内表面. 若交界面的两个空间区域至少一个是金属区域，则只需要在表面上定义电流，用 Δij=0表示；当交界面的两个空间区域均为介质时，还需要定义磁流，用Δij=1表示.

图1 任意交界表面与其两侧体积区域示意图Fig. 1 An arbitrary surface with its internal and external regions

1.2 DG 方法

在式(1)、式(2)所表示的原方程中所有边界上建立方程(10)，并乘以 −jαijαii0/ki加到原方程中，用同样的基函数进行离散，以消去式(7)L算子元素中的第五项基函数是半RWG 的计算.

对于复杂目标，使用MLFMA 来加速计算[23]. 对于DG 建立的离散方程同样适用. 唯一的区别在于边界的半RWG 需要进行一个三角形的积分计算.

1.3 预处理方法

多区域目标SIE 方程迭代计算的收敛速度较慢，因此需要进行合适的预处理. 预处理矩阵的定义如下：

图2 多区域交界处示意图Fig. 2 The junction of multiple regions

图3 介质球体不同算子矩阵块内元素模值随距离约束的变化Fig. 3 The variation of modulus value with distance constraint of a dielectric sphere

数值实验发现，在K 算子矩阵块中使用式(13)的预处理方式和原DSP 的预处理方式在迭代速率上相近，但是预处理矩阵元素进一步减少. 结合之前L算子矩阵块的预处理方法，简称这种方法为 ODSP.

矩阵块中的未知数为N，则近场矩阵元素个数为O(N2). 式(12) 中距离判断与介质波长有关，因此其矩阵元素数量为O(N)，由于有很多元素仍被约束在距离判断内，O(N)的实际系数很大. 式(13) O-DSP 中矩阵每一行只会保留4 个或2 个元素，因此整体元素数将小于4N，最终整体的预处理矩阵元素数将会明显减少，且介质表面未知数越多，减少效果越明显.

2 数值结果

利用广义最小残差 (generalized minimum residual,GMRES)求解器来进行仿真，Krylov 子空间的大小为100，迭代残差为1 0−3. 预处理求逆使用大规模并行求解器(multifrontal massively parallel solver, MUMPS)，计算平台为2.2 GHz CPUs 和 1 TB 内存的 Intel Xeon E7-4850.

如图4 所示，半径为0.5 m 的介质球，相对介电常数为5，被分为4 个子区域，剖分尺寸为0.005 m，为介质波长的11/100，频率为300 MHz 的平面波沿-Z方向入射. 利用DSP 和O-DSP 对 VV 极化方向的双栈雷达散射截面(radar cross section, RCS)(记为VV-RCS)进行对比计算，计算结果如图5 所示. 可以看出，DSP 和O-DSP 数值计算结果均很好地吻合了理论计算的Mie 求解，不会对求解结果的精度产生影响.

图4 介质球的区域分解形式Fig. 4 Domain partitioning for the dielectric sphere

图5 介质球的双栈VV-RCSFig. 5 The bistatic VV-RCS of the dielectric sphere

L算子的距离约束不变，为介质波长的1 /2，令K算子矩阵块内元素受不同的距离约束，对比其预处理内存和迭代次数，结果如图6 所示. 可以看到，当距离阈值在介质波长的1/10～1/2 时，迭代次数几乎不变，但元素个数随距离的减小大大减少，说明去掉含奇异点残留项的元素不会对迭代产生很大的影响.当距离阈值为介质波长的3/50 时，处于是否包含奇异点残留元素的临界，迭代次数发生了较为明显的改变，因此有保留这些元素的必要性.

图6 K 算子矩阵迭代次数和元素数量随距离约束的变化Fig. 6 The iteration numbers and element numbers of K operator matrix block, as a function of distance constraint

表1 对几种不同预处理器的数值效果进行了对比. 对比的稀疏策略(sparse strategies, ST)有如下四种：

表1 不同预处理器的DG 方法计算数值效果对比Tab. 1 Comparison of the n umerical performance of the DG solution with different preconditioner

由表1 可知，和NP 相比，所有的预处理器都增加了收敛速度，其中NFP，DSP，O-DSP 效果最好. 这三种收敛速度较好的预处理器中，O-DSP 矩阵元素数量最少. 和DS-2BDP 相比O-DSP 收敛速度极快，说明K算子矩阵块中有奇异点残留项的元素对于矩阵的收敛十分重要，即使数量并不多. 同样使用ST3 作用在L算子矩阵块，迭代速率明显下降，说明L算子矩阵块需要保留较多的矩阵元素.

图7 为图4 中的介质球子区域数量分别为4、8、16 和32 的分解情况. 不同分解区域数对DSP 和O-DSP 的迭代次数和元素比率的影响如表2 所示.区域数越多意味着边界半RWG 越多，K算子矩阵块会保留更少的元素. 从表2 中可以看出，两个预处理器的迭代速率几乎是一致的，说明子区域的数量并不会影响O-DSP 的效率.

图7 介质球的不同区域分解Fig. 7 Domain partition schemes for a dielectric sphere

表2 不同分解区域数对DSP 和O-DSP 的迭代次数和元素比率的影响Tab. 2 Comparison of the iteration numbers and element ratios of the DG solution with DSP and O-DSP for different decomposed spheres

如图8 所示，区域数量为4 的介质球内嵌不同个数半径为0.15 m、剖分尺寸均为0.005 m 的金属球.频率为300 MHz 的平面波沿-Z方向入射，介质球内嵌不同个数的导体块模型的双栈VV-RCS 结果如图9所示. 从图9 可以看出，使用DG 和O-DSP 的预处理器计算的数值结果很好地吻合了商业软件FEKO 使用共型剖分计算的结果. 导体块数量分别为2，4 和8 时三种预处理器迭代次数和元素个数对比如表3所示. 对比DSP，O-DSP 的迭代数有轻微的增加，而矩阵元素数量明显减少. 由此说明，O-DSP 仍然适用于多区域的目标.

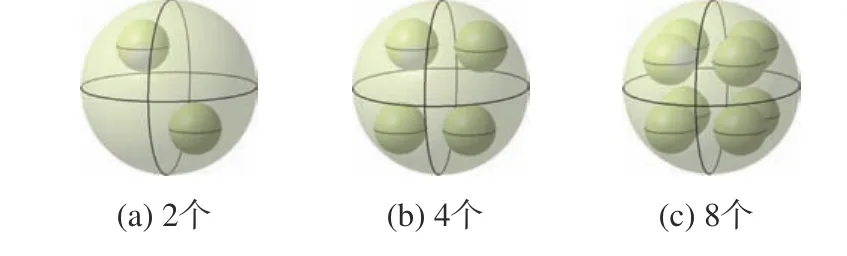
图8 介质球内嵌不同个数的导体块模型Fig. 8 Different numbers of conducting spheres embedded in one dielectric sphere

图9 介质球内嵌不同个数导体块模型的双栈VV-RCSFig. 9 The bistatic VV-RCS for the model of multiple conducting spheres embedded in one dielectric sphere

表3 导体块数量不同情况下三种预处理器迭代次数和元素个数对比Tab. 3 Comparison of the iteration numbers and element numbers by 3 different preconditioners with different numbers of conducting spheres

图10 所示为一个简化的射频芯片模型，包含了所有射频芯片内部的基本结构. 介质长方体模型尺寸为20 mm×20 mm×5 mm ，介电常数为 2.5，内嵌间距为 1 mm 的 5 片金属片，其中第一层和第五层用 4个金属圆柱相接作为整体的支撑，第一层和第二层之间由过孔相连，第三层和第四层之间是介电常数为4.2 的介质体. 剖分尺寸为细金属柱0.3 mm，其余部分0.5 mm. 一共分为 17 个 DG 区域，总未知数为 85 970 个.

频率为 40 GHz 的平面波沿-Z方向入射，使用CTF 方程计算，使用O-DSP 作为预处理器， VV极化方向的双栈 RCS 如图11 所示，验证了方程的计算正确性. 迭代收敛速度如图12 所示， DSP 和O-DSP 的迭代次数分别是 149 和153 ，略有差异，两者明显快于NP 的收敛速度. DSP 的矩阵元素数量是 78 061 756，O-DSP 为 46 922 730，数量明显减少.

图11 射频芯片模型的双栈VV-RCSFig. 11 The bistatic VV-RCS of the radio frequency chip model

图12 使用不同预处理器求解射频芯片模型的迭代收敛情况Fig. 12 Convergence histories for the radio frequency chip model under different preconditioners

图13 所示为四旋翼无人机模型的区域分解示意图，四个旋翼和支架是金属的，机身是相对介电常数为4 的介质体. 飞行器长宽约为2 000 mm 和830 mm.12 个子区域的总未知数为415 223 . 介质处的剖分为6 mm，一般导体的剖分为8 mm，旋翼处由于太细剖分尺寸为6 mm.

图13 四旋翼无人机模型的区域分解示意图Fig. 13 Illustration of subdomain partition scheme of a fourrotor aircraft model

频率为 4 GHz 的平面波沿-Z方向入射， VV极化方向的双栈 RCS 如图14 所示. 可以看出，O-DSP的 DG 方法和FEKO 符合良好.

图14 四旋翼无人机模型的双栈VV-RCSFig. 14 The bistatic VV-RCS of the four-rotor aircraft model

图15 为利用NP，DSP 和O-DSP 求解四旋翼无人机模型的迭代收敛情况. 可以看出，DSP 和O-DSP均快速收敛，二者速度相近. 表4 为 DSP 和O-DSP预处理器计算四旋翼无人机迭代次数和矩阵元素数量对比，其中O-DSP 矩阵元素数量明显减少.

图15 使用不同预处理器求解四旋翼无人机模型的迭代收敛情况Fig. 15 Convergence histories for the four-rotor aircraft model under different preconditioners

表4 DSP 和O-DSP 预处理器计算四旋翼无人机迭代次数和矩阵元素数量对比Tab. 4 Comparison of the iteration numbers and element numbers of the DG solution with DSP and O-DSP for the fourrotor aircraft model

3 结 论

本文使用DG 方法来求解多区域目标问题，并使用O-DSP 来提高仿真效率. 优化的预处理矩阵根据积分微分算子的不同数值特性，分块进行更恰当的预处理构建. 数值算例证明了预处理器的灵活性和准确性. O-DSP 相比DSP 拥有相近的迭代次数和更稀疏的结构特性，由于K算子的预处理矩阵块使用了一种更精准的判断方式保留了恰当的元素，因此ODSP 是一种更加有效的计算多区域目标散射的预处理方式.