用于并联机器人定位抓取的双目视觉算法实现＊

任建华 张宁可 高瑞贞

（河北工程大学机械与装备工程学院，河北 邯郸 056038）

工业机器人结合双目视觉模仿人眼去感受现实世界的真实场景，已经成为工学、医学等交叉学科的新型技术。对于工业机器人，如何快速实现对工件的定位抓取已经成为行业发展的关键性问题[1-3]。参考国内外研究现状，有关机器人定位的研究多数集中在自主定位方面，常见的是结合激光雷达、三维扫描仪等传感器[4-6]进行点云重构计算。该类方法当中，多数过程采用补偿技术结合运动学分析进行位姿计算估计，可以有效地提高定位精度[7]。但是成像范围小、设备投入昂贵等因素，以至于得不到大规模推广应用。其中双目立体视觉技术以设备简单、投资少等优点成为当前机器人视觉定位研究的热点[8]。

并联机器人属于工业机器人的一种，相比传统的工业机器人，并联机器人具有更快速度、更高精度和刚度等优点，采用末端执行器定位的方法。在机器人定位图像立体匹配中，对于窗口半径选取的变换、像素计算以及视差计算等操作具有较好的可行性。但在实际的工作环境中，如外部光照、内部弱纹理特征以及视差图不连续等一些因素，都会影响立体匹配的精度结果，导致三维重建不佳。其中对于弱纹理区域，由于图像局部分辨率变化，加上光照不均等因素，就会导致计算的纹理结果有较大偏差、误匹配率增高和出现“空洞”等一些问题。针对弱纹理区域存在的缺点，很多研究学者在局部算法方面也做了众多研究。Gómez-Espinosa A[9]基于深度RGB 传感器获取对象表明颜色，结合立体视觉进行模型重建，该方法虽提高了焊接轨迹的定位识别精度，但耗资较高，应用不广泛。陆明军[10]等将弱区域分类，将引导滤波结合视差融合，在保证匹配率的情况下具有更高的匹配精度。Liu H[11]等运用梯度增强的方法对引导滤波进行改进，通过自适应“十”字窗口进行代价聚合，提高匹配精度，但对引导滤波边缘保持性的缺点有待考虑。郁怀波[12]等根据不同区域像素的颜色选择性赋值系数，以树形结构算法为基础，进行代价聚合计算，在弱纹理区域取得了较好的匹配结果，但对于匹配窗口、权值计算等都是采用人为设置，缺少一定的不确定性、灵活性。传统的稀疏点云立体匹配算法是通过获取视差图进行三维重建，周泩朴[13]以此为基础进行分析和改进，虽然整体的准确效率提高了，但是在特征点提取不足的缺点依旧存在。Feng H[14]等结合ADCensus 立体匹配算法对特征点进项滤波处理，有效地降低了像素点局部噪声的影响，提高鲁棒性。鲁光明[15]等针对视差突变的问题，采用AD 算法变换结合代价聚合SGM 改进，提高了弱纹理区域匹配效率，但缺乏实时性的改进。赵春晖[16]以特征点为基础，选取主方向尺度信息作为匹配代价数据，提高匹配率，该算法在旋转和缩放的情况下表现良好。

综上分析，结合传统工业机器人二维情况下存在定位抓取准确率低、适用性差等缺点，引入三维信息到机器人定位抓取中。设计一种将梯度信息、自适应双边滤波应用到SGBM 算法当中，以提高三维点云质量为基础，提高机器人的准确定位抓取方法。该算法解决了在代价计算阶段对于弱纹理区域，存在的像素变换不连续、普通算法视差有残缺等问题。可以降低图像在立体匹配时的误差，较好地抑制了弱纹理区域像素变化对代价的影响，增强了噪声、光照因素对立体匹配的稳定性，提高了视差图的匹配效率和质量精度，实现了工件任意摆放下的准确定位抓取。

1 双目成像原理

在图像处理中，单目相机是无法估计像素的深度恢复三维模型坐标的，但是类似于人眼的双目相机，可以通过引入更多的约束求解出图像的三维模型坐标。双目相机同时从不同角度拍摄物体，物体表面上的像素点会被映射到投影平面，其模型原理如图1。

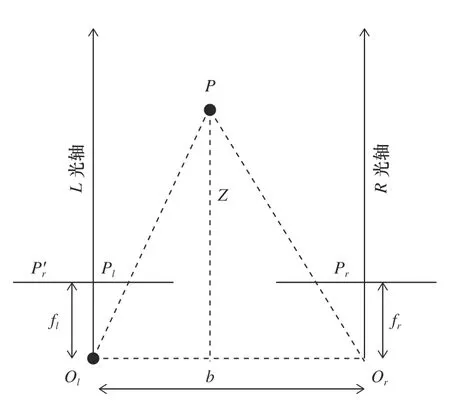
图1 双目立体相机模型

图中以左相机为原点。基线b：相机光心距离，f：相机焦距。假定像素点P在左右成像面交点横坐标为Pl、Pr、xl、xr。结合三角形相似原理，由POlOr组成的三角形可以得出俯视图上P点到成像平面的距离，也就是该点所在的深度信息。其结果为

由结果可知，其中fb乘积是固定不变的，左右成像平面横坐标xl-xr越小，深度值Z越大，相反越小，这种方式求得的Z又被称为视差。在双目立体匹配中，左右相机就是通过这种方法根据左右像素点坐标，通过计算找到三维空间中的同一点像素，进而求算出图像的视差图进行三维点云重建。进一步，以手眼标定算法实现物体坐标在相机、机器人之间转换，完成定位。其总的流程如图2。

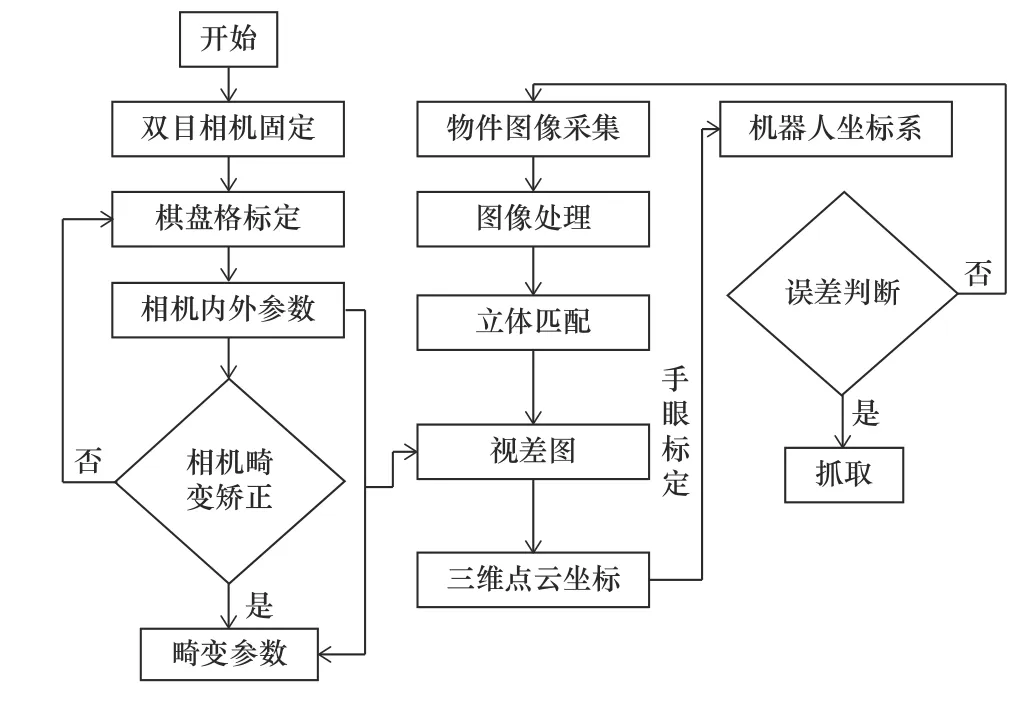
图2 整体定位算法流程图

2 算法的实现描述

2.1 匹配代价计算

匹配代价计算是对左右两幅图的相似性度量。常见的有AD、SAD、SSD 和NCC 算法，其中基于差的绝对值和（sum of absolute difference，SAD）匹配代价算法计算量小、速度快，能够满足实时响应的要求[17]。本文在此基础上又融入梯度信息，在视差图像不连续区域中梯度可以有效地解决误匹配问题。首先以SAD 算法构建一个窗口遍历左右图像，计算左右匹配图像窗口内所对应像素之差的绝对值之和，通过阈值比较，最小值即为颜色匹配代价进行视差计算。其公式表示为

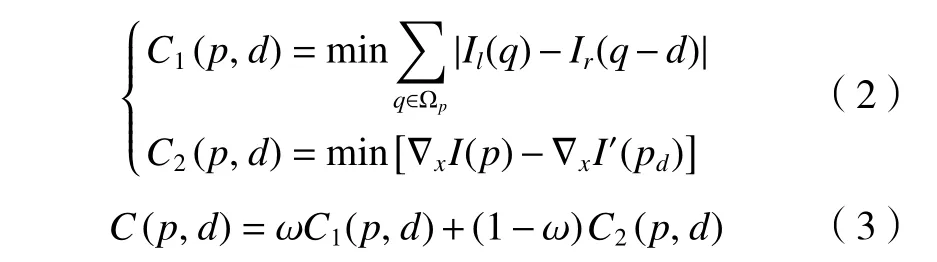
式中：C1(p,d) 为 SAD 匹配代价、C2(p,d)梯度匹配代价、C(p,d)融合匹配代价。受文献[18]启发，根据SAD 窗口边长选取的不同，将权重系数 ω引入一个调整系数K，这样在融合代价计算时可更好地分配权重。可定义为

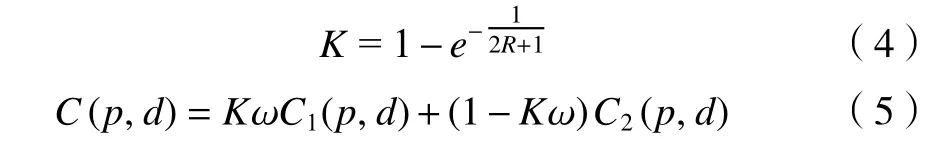
式中：像素点选窗口R越大，则对应的调整系数就越小，从而所在的SAD 匹配代价权重就越小，梯度代价权重就偏大。因此，对于那些在弱纹理区，可以更好地使用梯度代价来进行计算。

2.2 自适应双边滤波代价聚合

2.2.1 传统双边滤波

双边滤波（bilateral filter）[19]其工作也是采用加权平均的计算方式，主要是以待处理像素点与四周像素点欧式距离及像素亮度作为权重。在滤波器分类中，双边滤波属于非线性滤波，其数学模型公式为

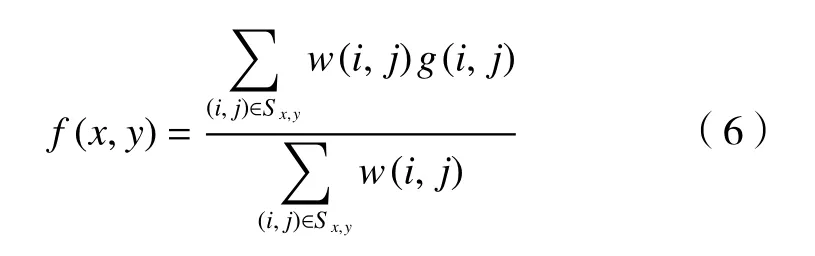
式中：S(x,y)所 代表的是以像素点为中心 2R+1为边长的方形领域坐标集合，和SAD 窗口的选取f(x,y)为滤波处理后图像在点 (x,y)的 灰度值，g(i,j)为未经处理的噪声图像灰度值。在整体的算法当中综合权重w(i,j)由 空间域权重ws(i,j)、领域灰度权重wr(i,j)组成，可表示为

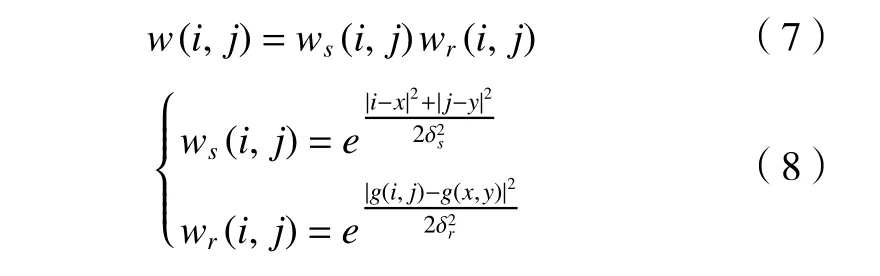
对于参数R、δs、δr是影响双边滤波器大小的主要因素。当滤波器窗口半径R越大滤波程度就越大；空间域标准差 δs越 大，与其对应的空间高斯函数ws权重越分散，虽然去噪效过提高了，但图像边界越模糊；领域灰度标准差 δr越大，与其对应的灰度相似度函数wr对灰度的要求就越低，颜色平均区域越模糊。选取样品局部区域为验证对象，设置R=4，空间域标准差 δs=2领 域灰度标准差 δr=0.1的参数效果如图3 所示。可以看出图3c 双边滤波和中值滤波相比纹理变换边界更加清晰。对于不同的噪声图像，要想获取更清晰的图像需要手动设置参数，很少存在“通用”的现象，也正是因为这样繁琐的步骤，提出自适应双边滤波。

图3 噪声对比图

2.2.2 自适应双边滤波

高斯滤波是最常见，也是最原始的一种滤波器，它是以待处理像素点与四周像素点的欧氏距离作为权重计算的一种算法。与其对应的数学模型是二维高斯函数，其分布是一维高斯函数分别在X轴、Y轴上的乘积。

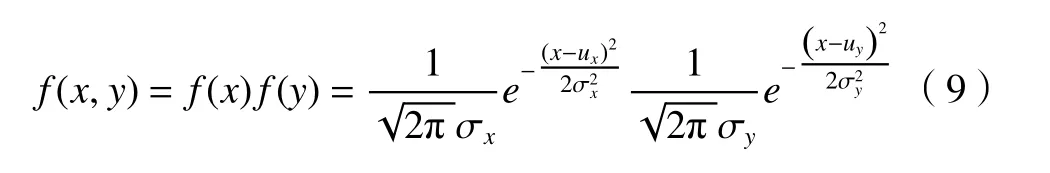
不难理解服从正态分布的一维高斯函数具有对称性原则，且二维高斯函数结合空间Z轴则有旋转对称性，函数效果如图4 所示

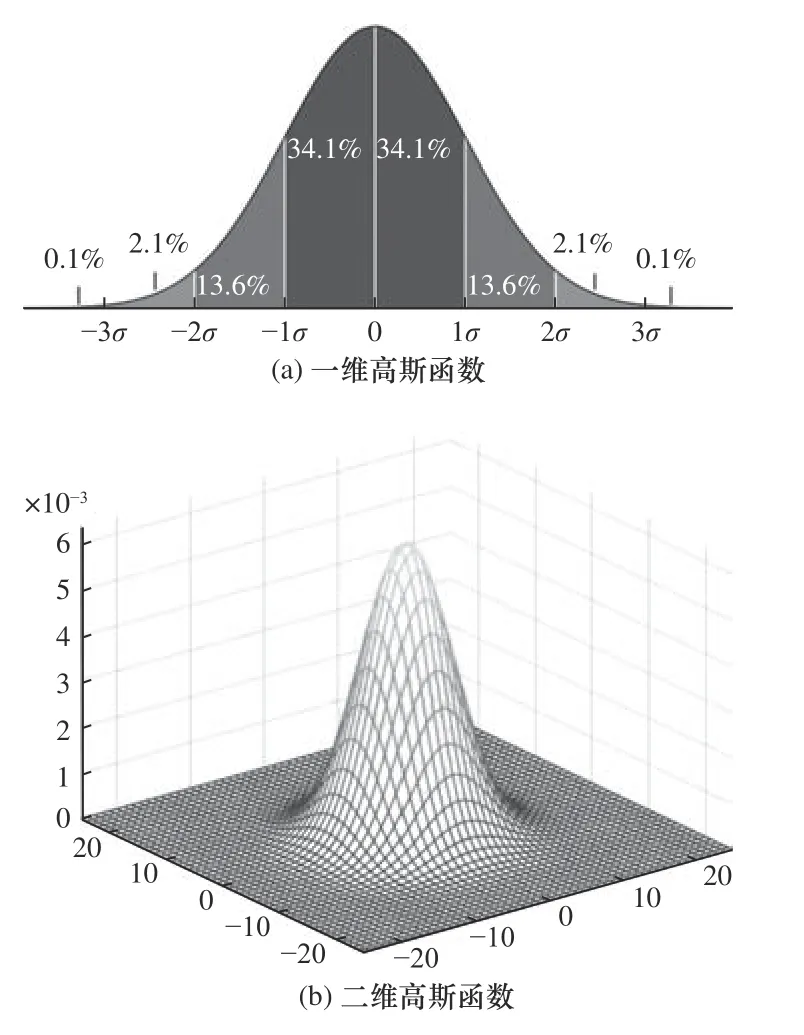
图4 函数效果图

双边滤波综合了高斯和结尾均值滤波，同时考虑空间域、邻域之间的关系。

（1）空间域标准差

结合高斯函数，抛开灰度标准差，可以看出空间域标准差 δs与所选窗口边长的大小还是存在一定的线性关系。同理高斯函数分布，从图4 中可以看出正态分布95%的量都分布在 [-2δs、2δs]之间，冗余的并没有太大影响。当标准差 δs越小，图形分布越集中。为了获取更多的目标像素作为样本数据，可设定

式中：r为常数经验值其小于窗口半径R，与传统相比，95%的分量都会落在半径为Rr的区域内，可以有效地解决图像权重分散、模糊的问题，其余分布在边缘窗口的像素点主要是参与噪声的计算。

（2）邻域灰度标准差

与空间域标准差相比，灰度标准差对双边滤波的处理效果具有更大的影响。当标准差值越大，图像的去噪效果越好，但是图像清晰度会更差。根据文献[20]灰度标准差 δr和 噪声差值 δz存在一定的线性关系，该文献进行了不同噪声下图像灰度标准差的取值，经试验 δr/δz的比值大致分布在[2,3]之间，为了获得更多的细节信息，选取 δr=2δz。结合文献[21]噪声方差的初步估计，F-NLE 方法在图像处理中，为了降低纹理边缘计算时得出的二阶导数对初步估计结果的影响，所以采用2 个Laplacian 掩模算子差值N来评估噪声。

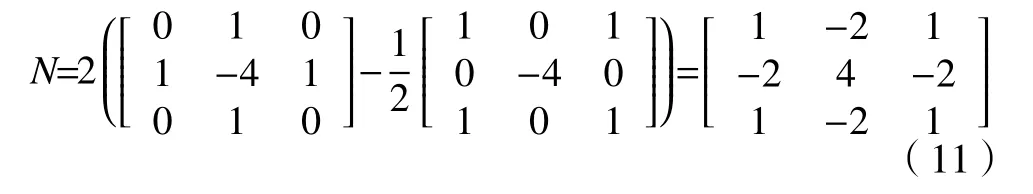
则图像噪声标准差的计算 δz表示为

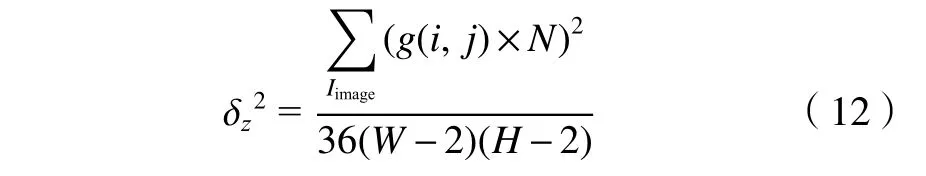
即灰度标准差

以VS2019 为编程实验平台，首先取窗口R=4，常数r取1，得出的结果如图3 所示。通过图3 中c 和d 相比，改进后的自适应双边滤波处理结果与事先设定参数的传统滤波处理结果极为相似。可以得出，改进后的算法实现了空间域标准差和邻域灰度标准差的自适应调整，为后面做立体匹配特征提取提供了需求。

2.3 代价计算

经过代价聚合后利用Winner-Take-All(WAT)算法策略，选取最小匹配代价视差值作为初始视差

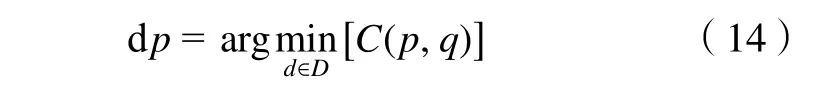
式中：D表示计算范围中所有可能的视差值。

2.4 视差后处理

SGBM 算法通过WTA 代价计算后，所得的初始视差图并非最终结果，还需要进一步的后处理操作剔除异常匹配点。首先，通过视差值进行的置信度检测，可以去除相差悬殊的代价值；结合亚像素插值使图像视差更平滑；再以左右一致性测量为准则，判定初始视差图中的最大误差像素点，其定义公式为

式中：dl(p)是p点在左视差图中的视差值，相反dr[p-dl(p)]为右视差图的视差值，如果通过比较不能满足公式（15），则视为像素p点所在视差为无效视差值。

3 物件对象处理

3.1 基于外轮廓的形心点定位

采用圆柱工件为验证对象，结合外观轮廓形状以及三维重建后点云模型，选取其上表面中心作为机械手的定位点，对于像素坐标系下定位点 (u,v)的定义求解方式为

为了求解物体中心像素坐标，首先对目标图像的外轮廓进行二值化处理，其结果如图5 所示，结合式（16），通过计算可以分别得出左右图像的像素形心坐标 (ul,vl),(ur,vr)，其两点形心坐标在实际三维点云模型中即为中心点。

3.2 相机坐标获取

为了获取在图像识别特征配准后，所做标记点Z方向上的三维坐标信息，利用改进算法分别对方形、圆柱形物体进行立体匹配处理。对其视差图和三维点云如图6 所示。在物体上选取的5 个特征点为分析对象，以小孔成像原理为基础，利用像素下坐标信息结合齐次坐标式（17），畸变矫正式（18）以及式（1）计算出物体相对于主（左）相机下的三维空间坐标Xl、Yl、Zl。其中xl、yl为 像素坐标，f为焦距，ul、vl为相机内参数，实验数据如表1。

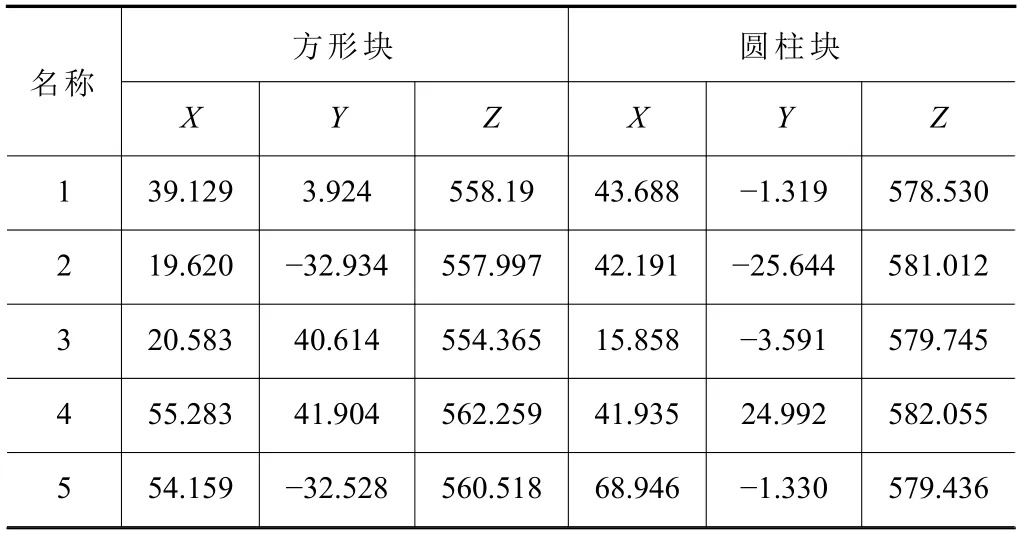
表1 标记点相机下三维坐标

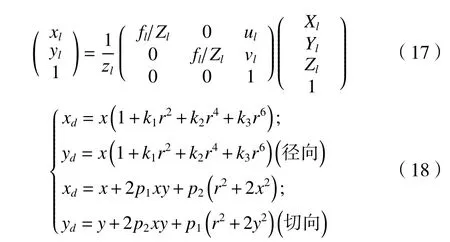
3.3 三维点云坐标转换

根据实际并联机器人识别分拣系统实验，防止工作过程中机械手臂、相机之间发生冲突，所以采用Eye in Hand 的方式进行标定。将采样点得到的坐标信息通过此方法转换到机器人坐标系下。其转换公式如下

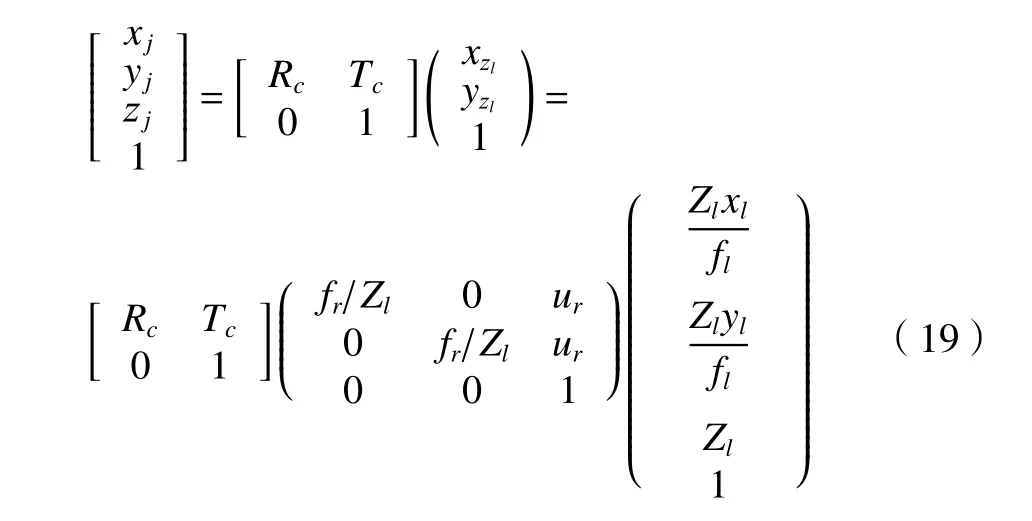
式中：Rc、Tc分别为相机坐标系到机器人坐标系的旋转和平移矩阵。将获得的三维坐标信息通过上位机输送给并联机器人，在驱动器下完成物件的定位抓取。其变换后的坐标信息如表2 所示。

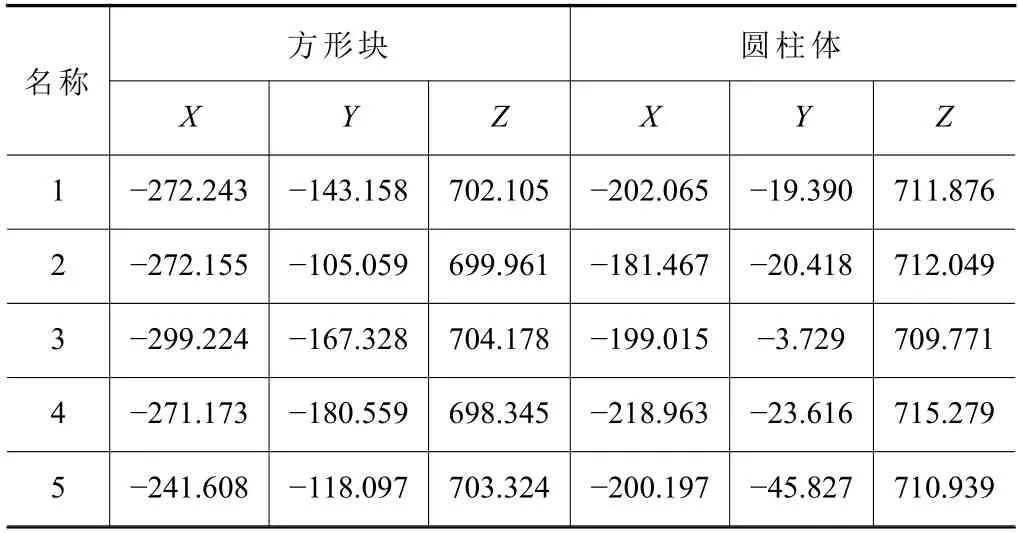
表2 标记点机器人下三维坐标

4 实验结果与分析

4.1 视差图算法验证

为了验证改进后加入梯度信息的代价计算算法，以及自适应双边滤波代价聚合算法在SGBM 算法中的真实性，本文先对Middlebury 平台四组标准图像进行实验，然后再应用到实拍图像上进行分析算法的可行性。以误匹配率PBM 以及计算时间T来评价表明结果的好坏。其中对PBM 的定义为

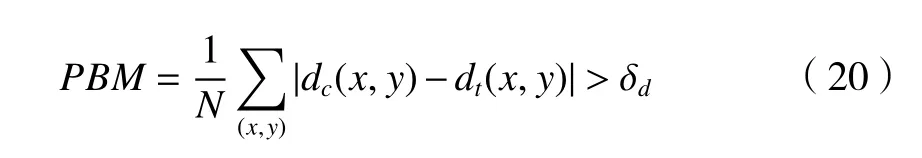
首先选取标准数据集中双目矫正后的Art、Baby、Cloth、Aloe 为实验对象。其SAD 窗口选择为9×9，对比的时候其他参数一致,其实验结果如图7。

观察图7c、d 和e 可以看出，在弱纹理过度区域，本文优化改进算法可以弥补BM、SGBM 的不足，在弱纹理区域能够把一些边缘轮廓进行填充，图中红色圈仅进行了局部标注说明。本文优化方法及其他两种算法视差图计算时间T 如表3 所示、误匹配率对比如表4 所示。

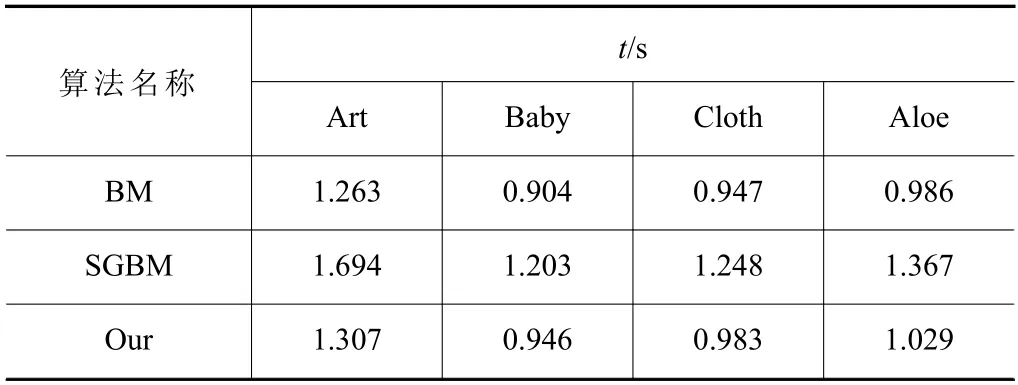
表3 计算时间对比

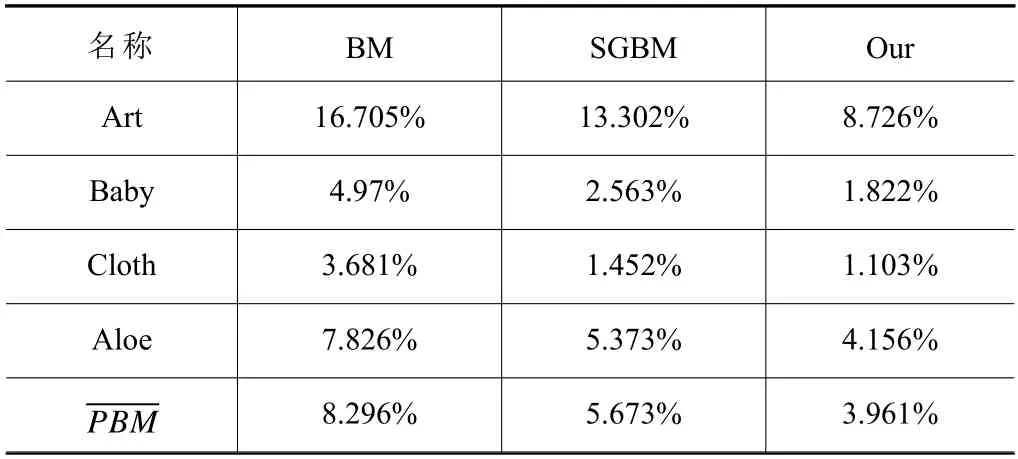
表4 误匹配率PBM

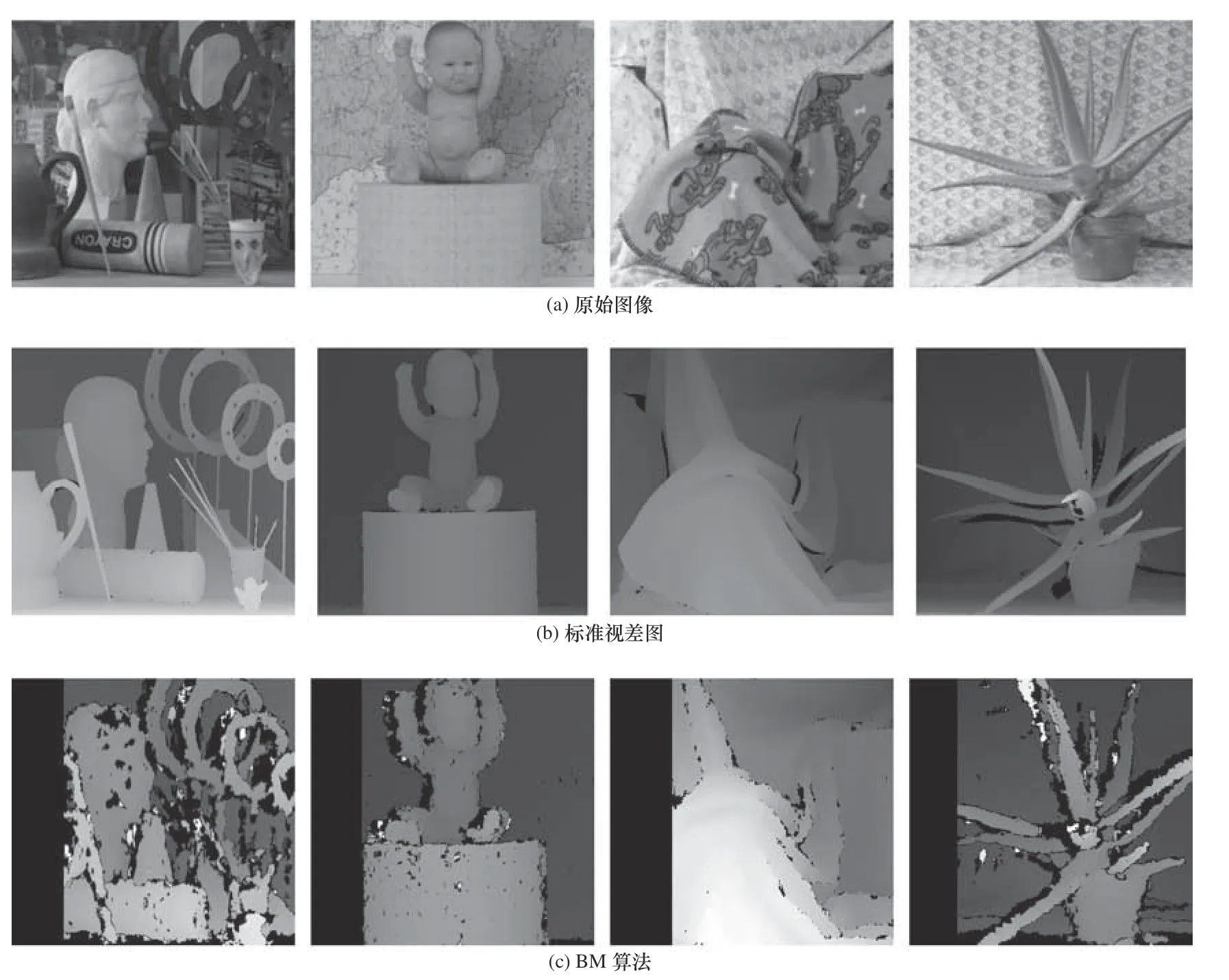
图7 立体匹配及优化算法实验结果

由表3 数据可以看出，对标准数据集图像的测试，改进后的立体匹配算法时间上虽然不及BM，但与传统算法相比，在计算时间上平均缩短了22.54%。表4 分析可以看出，优化改进后的算法较BM、SGBM 算法误匹配率更低，平均误匹配率降低了3.024%，更加接近标准视差图。

4.2 实际抓取验证

为了验证改进后算法的真实有效性，将其应用到并联机器人中，其实验结果如图8 所示。整个系统主要包括：上位机、工控机、拍照系统和机械手等。实验步骤：首先由相机拍照系统获取图像，经改进算法进行处理获取物体三维重建模型的坐标信息，通过手眼标定将相机坐标系下获得的信息转换到机器人坐标系下，应用上位机通信将物体形心坐标信息传送给并联机器人。并与BM、SGBM 下总体时间和效率两方面进行分析对比，从而验证了本文算法应用在机器人上应用有效可行性。

图8 实际抓取实验

图9 一共统计了20 组方形块和圆柱块随意摆放抓取时的相对误差实验数据，分析可以看出，对于表面纹理较为复杂的对象，其相对误差率平均可以控制在5%以下，对于表面光滑的对象，其相对误差率平均可以控制在3%以下，较比另外两种算法有了明显的改进。

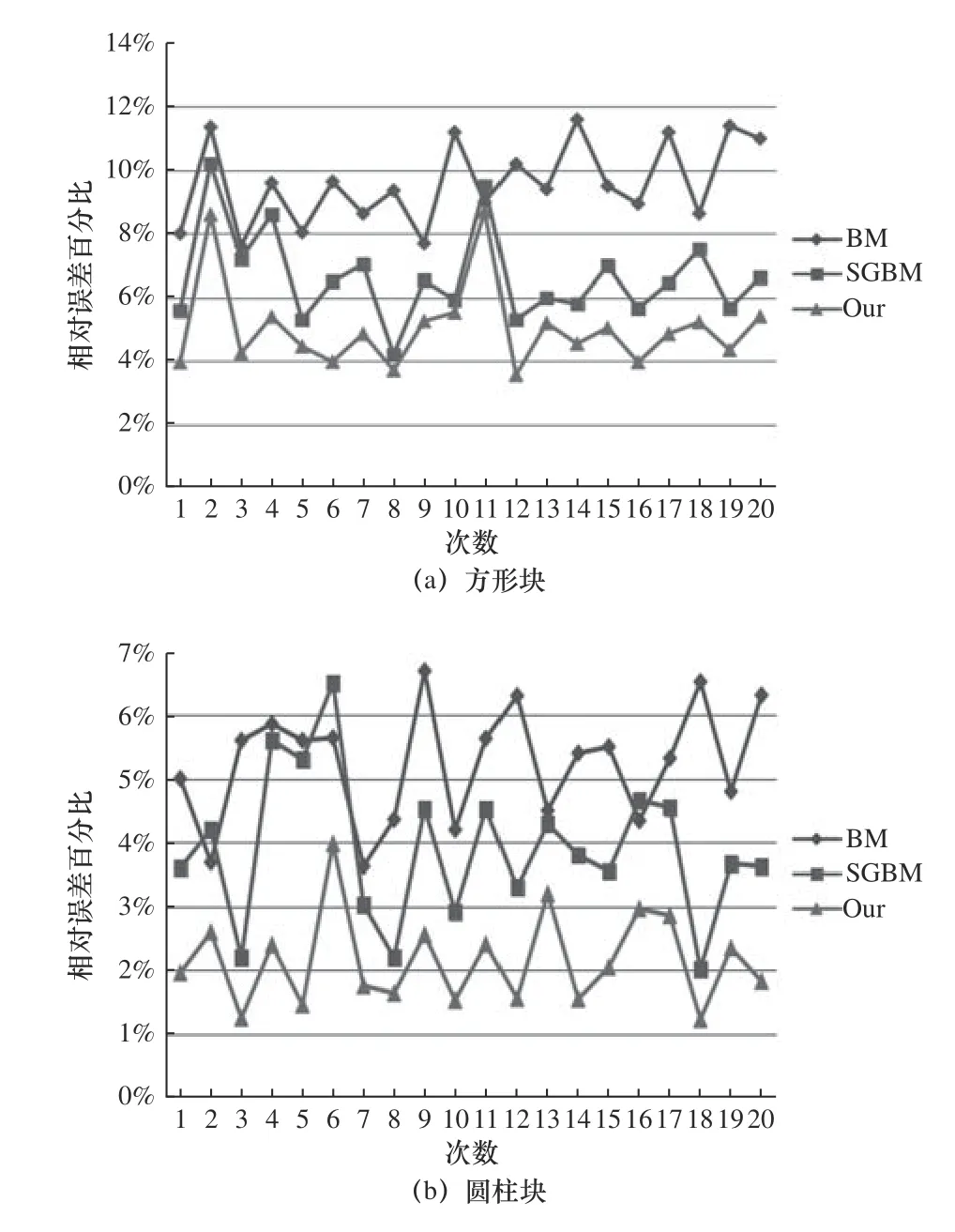
图9 抓取对象标记点测试误差分析

5 结语

针对传统机器人定位抓取中有关相机立体匹配方法的准确率低、匹配时间长问题，提出了一种机器人定位抓取的改进双目视觉算法。通过实验对比可以得出，对于弱纹理区域引入梯度信息到SAD算法当中，对于不同像素，通过调整系数K 更好地均分SAD 代价、梯度代价；以自适应双边滤波替换人为设置参数，最终得到匹配代价；进而提高三维点云的重建效果，促使机器人完成准确地定位抓取，通过实验验证可以将误差率平均控制在5%以下，具有不错的应用前景。