成形法加工螺旋锥齿轮切削力模型研究

罗 静 康先强

（①重庆理工大学机械工程学院，重庆 400054；②重庆理工大学汽车零部件先进制造技术教育部重点实验室，重庆 400054）

锥齿轮机床铣齿切削力研究一直是切削过程研究的重点问题，同时也是铣齿振动刀具磨损、工艺参数优化等研究的基础。目前对铣齿切削力建模的方法主要包括3 种：一是根据金属切削理论，将切削力表达为进给量、主轴转速和背吃刀量等加工参数的函数，但这种方法需要进行大量的正交实验，确定加工参数前面的系数；二是机械模型，将刀具切削刃沿轴向进行离散，对离散后的微段切削刃进行求解，对微段切削刃积分即可求解出刀具上的切削力；三是根据简化切削力模型，将切削力当作切削面积和切削力系数的乘积，其中切削力系数由刀具材料和齿坯材料决定。

对于上述模型，国外Yang Y[1]、Pradeep K B[2]、Korkut I[3]等学者分别对其进行了相应的应用。Andersson C[4]建立了一种适用于多齿加工的切削力模型，对各参数与总切削力之间的影响进行了分析。国内贾新杰[5]通过正交实验标定铣削力系数，并对瞬时切削面积进行推导，建立了成形法加工螺旋锥齿轮大轮切削力模型，但铣削力系数是通过正交实验进行标定，应用效率需要进一步提高。王勇[6]采用切入法加工螺旋锥齿轮大轮的原理，推导了齿坯、刀具和机床坐标系的关系模型。石锐[7]等人根据材料Johnson-Cook 本构方程和斜角切削理论，对剪切区的剪切应力进行计算，并结合瞬时切削面积构建展成法粗铣小轮的铣削力模型。Zheng F Y[8]等人对展成法加工螺旋锥齿轮过程中的未变形切屑面积进行了归纳总结，在此基础上提出了一种高效、准确的面铣切削力预测模型。

本文通过推导成形法铣齿过程中的瞬时未变形切削面积，结合剪切区应力计算结果，构建了成形法加工螺旋锥齿轮大轮的瞬时切削力模型，并设计实验对理论模型进行了验证。

1 成形法铣齿加工原理

成形法加工螺旋锥齿轮时，首先需要调整齿坯安装角和刀具位置，使其保持正确的相对位置。在铣齿加工过程中，齿坯和刀盘的相对位置保持不变，齿坯保持不动，刀盘旋转并沿着刀盘轴线方向进给，齿轮齿形取决于刀具形状，其加工原理如图1 所示。当完成一个齿的加工后，刀具退刀，齿坯旋转进行分度，并进行下一个齿的加工，循环该切削过程，直至完成所有齿的加工。

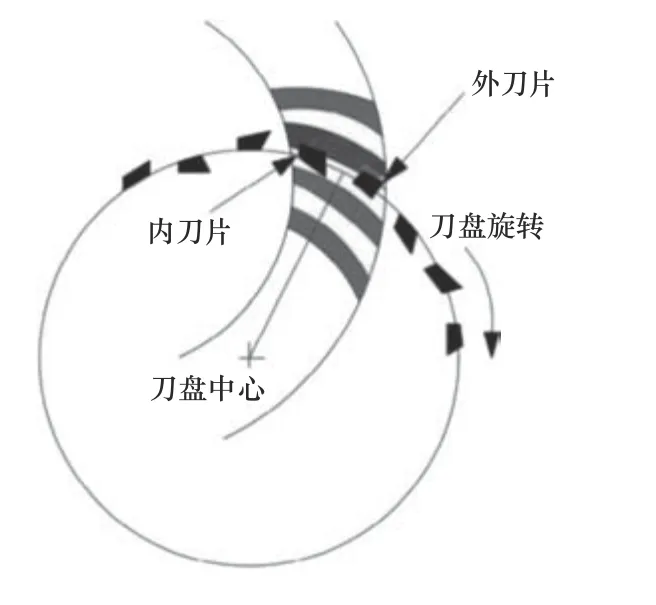
图1 成形法铣齿加工原理图

2 未变形切屑切削宽度和厚度计算

2.1 刀片产形面方程

在成形法加工螺旋锥齿轮大轮时，内外刀片切削刃绕着刀盘中心旋转形成两个圆锥面，建立其刀盘坐标系如图2 所示。

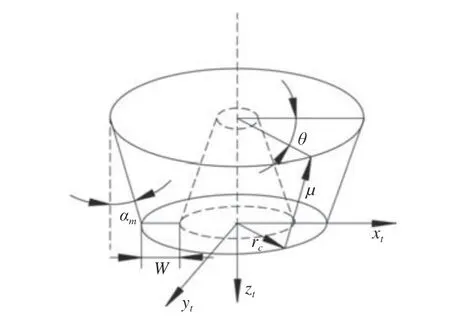
图2 成形法加工大轮刀盘坐标系

根据成形法加工大轮的刀盘坐标系，可得到内外刀片的产形面方程为

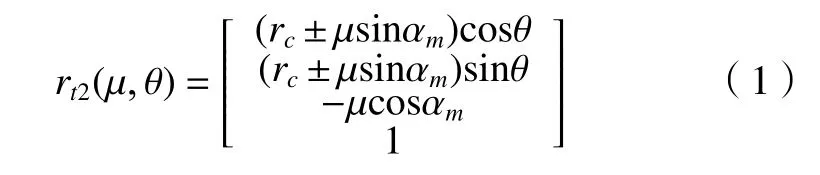
式中：(μ,θ) 为 刀片产形面上的动点参数；rc为内外刀片刀尖点处半径，其中rc=r0±0.5W，r0为刀盘名义半径，W表示刀错距，外刀取“ +”，内刀取“-”。αm为 内外刀片齿形角，m=(e,i)，其中e表示外刀取“+”，i表示内刀取“-”。

2.2 螺旋锥齿轮大轮面锥方程

螺旋锥齿轮切削加工过程中，刀盘上的外刀片和内刀片首先与大轮面锥接触，因此首先建立大轮面锥坐标系Sa，并在轴交错点处建立大轮坐标系S2。当齿坯完成设计后，大轮齿坯各参数值均为已知，如图3 所示。

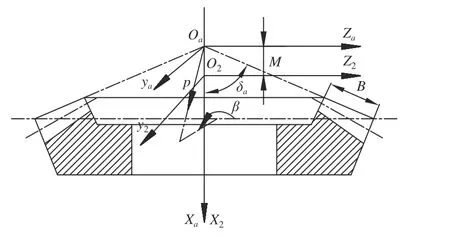
图3 大轮面锥坐标系及大轮坐标系示意图

根据大轮面锥坐标系Sa，可得到大轮面锥方程为

式中：(p,β)表 示大轮面锥上的动点参数；B表示大轮齿面宽；δa表示大轮面锥角；M为面锥顶点与轴交错点之间的距离。

2.3 成形法铣齿机床加工坐标系

图4 为成形法加工螺旋锥齿轮大轮的机床坐标系，其包含的锥齿轮机床调整参数分别为床位zj，水平刀位H、垂直刀位V、水平轮位X2和锥齿轮机床安装根锥角 δM2。

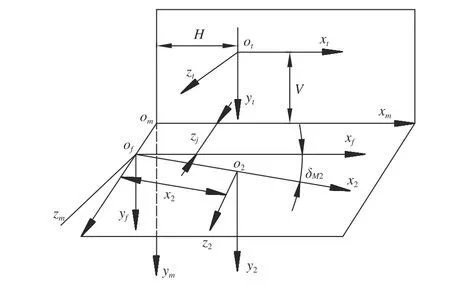
图4 成形法加工螺旋锥齿轮大轮机床坐标系

因此，刀片产形面方程可通过坐标转换，变换到机床坐标系中，其方程可表达为

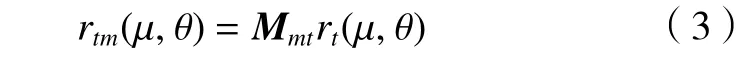
式中：Mmt为刀盘坐标系St变换到机床坐标系的转换矩阵。

同理大轮面锥方程变换到机床坐标系中，其方程为

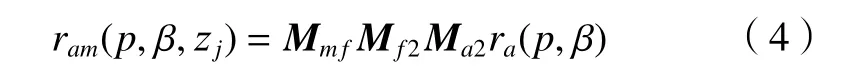
式中：Mmf、Mf2、Ma2为面锥坐标系变换到机床坐标系的转换矩阵。

因此，可得到在机床坐标系中，刀片产形面方程和大轮面锥方程的交线方程为

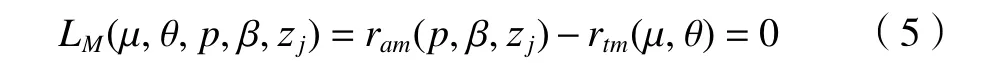
为了得到刀盘上内外刀片的切入切出角度，即内外刀片在切入切出角范围内对齿坯进行切削。因此，需对内外刀片的切入切出角度进行计算，刀盘切入切出齿坯的相对位置如图5 所示。

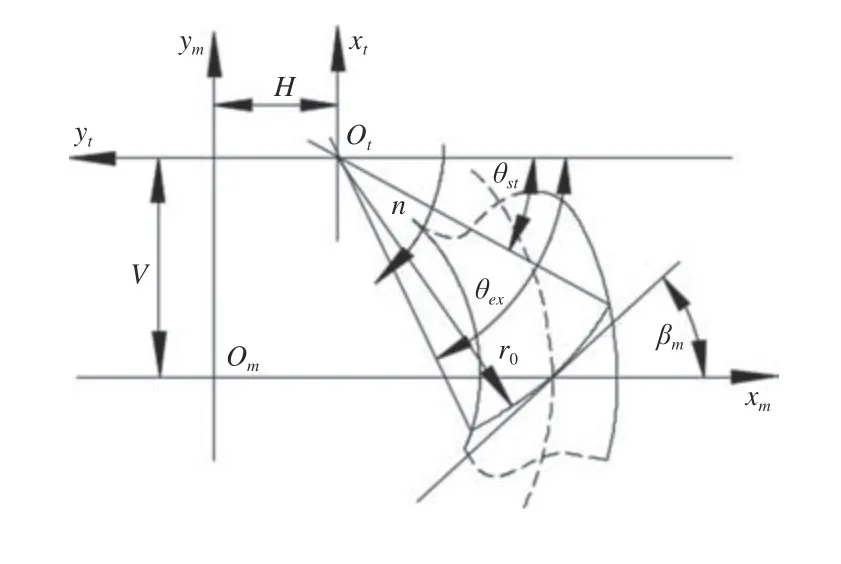
图5 刀具和齿坯相对位置示意图

因此，可求得切入角 θst、切出角 θex分别如式（6）、式（7）所示，其中k为刀盘转过的圈数。

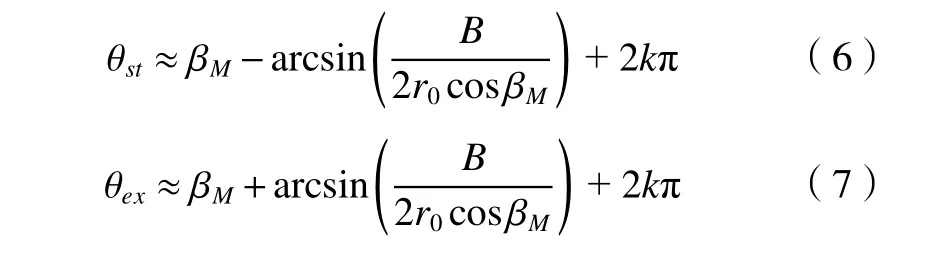
2.4 瞬时未变形切削宽度和厚度计算

在成形法铣齿过程中，为简化研究对象，假定在铣齿加工过程中，任意时刻只有单个刀齿参与切削，即相邻刀片刀刃之间的距离大于齿线长度，其满足任意时刻只有一个刀齿参与切削的条件为：

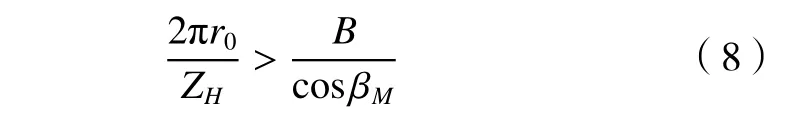
其中：r0为刀盘名义半径，ZH为刀盘上的刀齿数，B为齿面宽，βM为大轮中点螺旋角。

螺旋锥齿轮铣齿过程中，刀盘以转速n旋转，其切削方向为刀盘的切向，同时刀具沿着刀具轴线方向进给，当刀具处于大轮全齿高Hg位置时，刀具与齿坯进行接触，切削开始，当移动到床位Zj=0 时，刀片刀尖平面与齿槽底平面相切，完成一个齿的加工，刀具退刀同时齿坯进行分度，进行下一个齿的切削，不断循环直至完成所有齿的加工，刀盘上刀齿的分布情况如图6 所示。

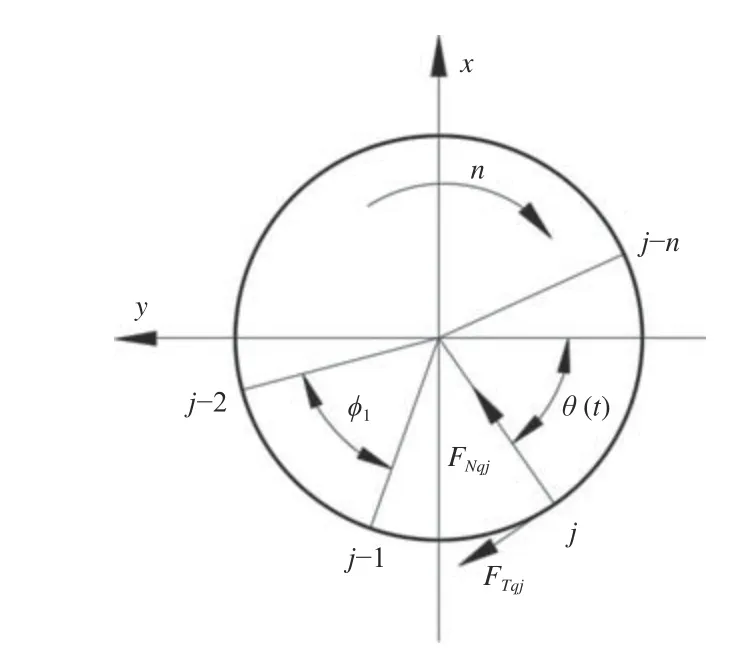
图6 刀片在刀盘上的安装位置示意图

其中，相邻刀片的夹角即节距角 φ1=2π/ZH，每齿进给量fc=f/(nZH)，床位zj(t)=Hg-fct。

则刀片j在任意时刻的转角为

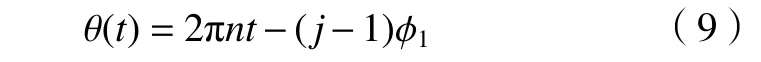
式中：j取奇数表示外刀片，j取偶数表示内刀，j=1,2,···,ZH。

对于外刀片而言，当轴向进给运动的床位保持在0 ≤zj(t)≤Hg时，且刀片任意时刻转角保持在2kπ+θst≤θ(t)≤2kπ+θex时（即在切入切出角范围内），其中k为刀盘旋转的圈数，将 (θ(t),zj(t))代入机床坐标系里所建立的交线方程中可求得uej(θ(t),zj(t))。

因此，外刀片主切削刃的瞬时未变形切削宽度和厚度分别为

由于在实际加工过程中，螺旋锥齿轮的齿槽是刀具顶刃切削形成，因此在计算中需要考虑顶刃的影响，其瞬时未变形切削宽度和厚度分别为

式中：Sb为刀顶宽，Sb=(0.5-0.75)W，W为刀错距。

同理可求得内刀片主切削刃的瞬时未变形切削宽度和厚度分别为

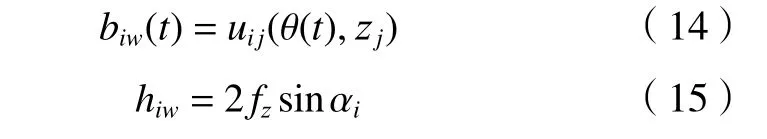
内刀片顶刃的瞬时未变形切削宽度和厚度分别为

其中：内外刀齿主切削刃和顶刃切削时的瞬时未变形切削宽度和厚度如图7 所示。

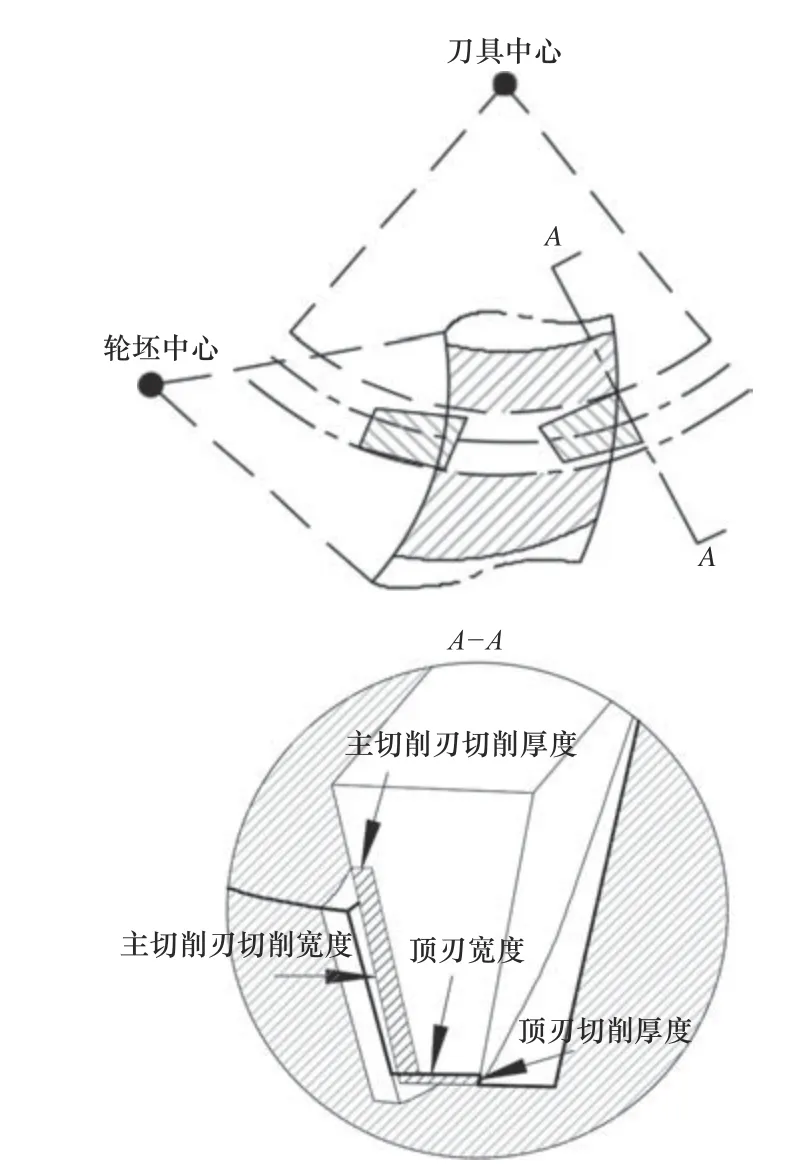
图7 瞬时切削宽度和厚度示意图

3 剪切区应力计算

JC 本构模型是一类描述应变、应变率、温度影响关系的函数，根据斜角切削理论及材料的JC本构模型可计算得到材料的剪切区应力τ即单位横截面切削力，其具体公式如下[9]。

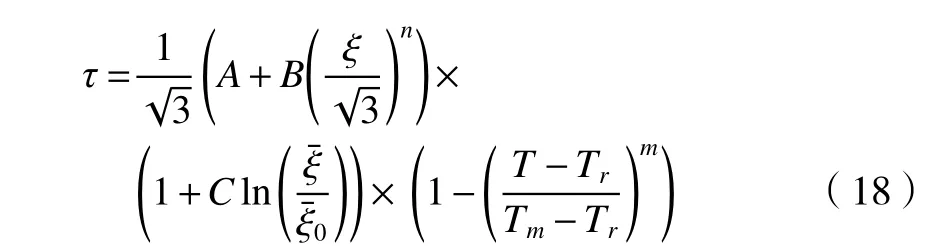
在等效平面上对非等分剪切区模型进行应用，可得到材料JC 本构方程中剪切区的剪切应变 ξ、剪切应变率计算公式为

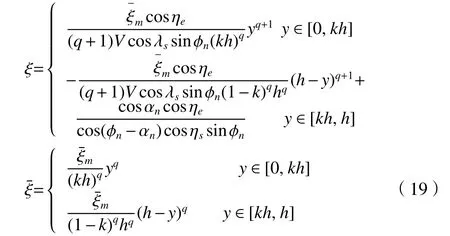
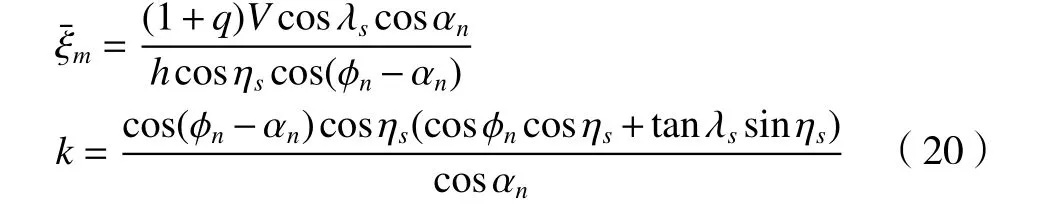
由于在成形法铣齿过程中，刀具的切削刃方向和切削速度方向并不垂直，成一夹角，因此满足斜角切削理论，因此可根据斜角切削理论对剪切流动角 ηs、等效平面角 ηe进行计算。

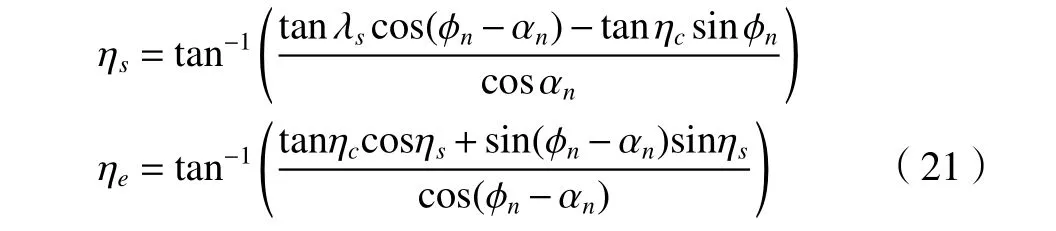
同理需要对法向剪切角 φn、法向前角 αn、流屑角 ηc的值进行计算。根据斜角切削理论，法向前角的计算公式如下。

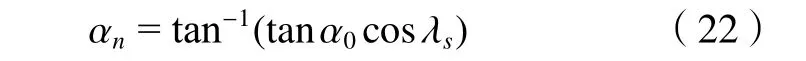
在斜角切削中，法向前角 αn、法向剪切角 φn、摩擦角 β满足Merchant 公式[10]。

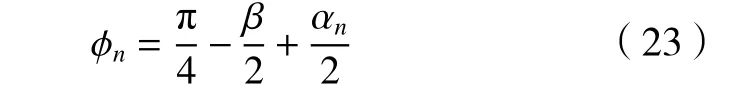
根据Schulz 公式[11]，刀屑面上的平均摩擦系数和摩擦角的关系为

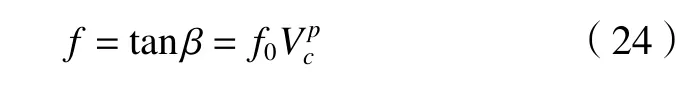
式中：f为平均摩擦系数，f0、p为常数值，取其典型值f0=0.704，p=-0.2048。

切屑速度Vc可根据斜角切削的理论公式计算得到

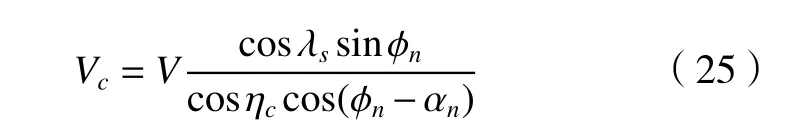
式中：根据Stabler 法则[12]，当刃倾角较小时(λs≤15。)，流屑角 ηc和刃倾角近似相等。本文所采用的刀具刃倾角为5°，满足条件，因此有

对于剪切区速度分布特性参数q，在进行塑性材料加工时，低速切削取q=3，高速切削取q=7[13];本文采用的齿坯材料为42CrMo4 结构钢，其本构模型常数为[14]A=595 MPa，B=580 MPa，C=0.023，m=1.03，n=0.133，=0.0011 s-1，Tr=1 793 K，Tm=293 K。

4 刀齿切削力建模

成形法铣齿过程中，刀片上所受到瞬时切削力的大小由齿轮齿坯材料的单位横截面切削力和瞬时切削面积决定，瞬时切削面积的计算取决于瞬时未变形切削宽度和厚度。因此，任意时刻t，刀片j上的瞬时切向切削力FTqj由主切削刃切向切削力FTqm和顶刃切向切削力FTqv合成；刀片j上的瞬时径向切削力FNqj由主切削刃径向切削力FNqm和顶刃径向切削力FNqv合成；刀片j上的瞬时轴向切削力FZqj由主切削刃轴向切削力FZqm和顶刃轴向切削力FZqv合成，其结果分别为

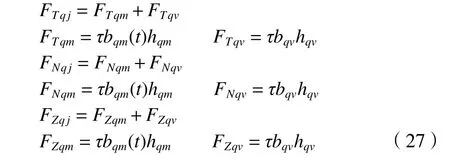
如图8 所示，将刀片j主切削刃和顶刃的切向、径向、轴向切削力分解到刀盘坐标系下的x、y、z这3 个方向，则第j个刀片沿坐标轴在3 个方向的瞬时切削力为

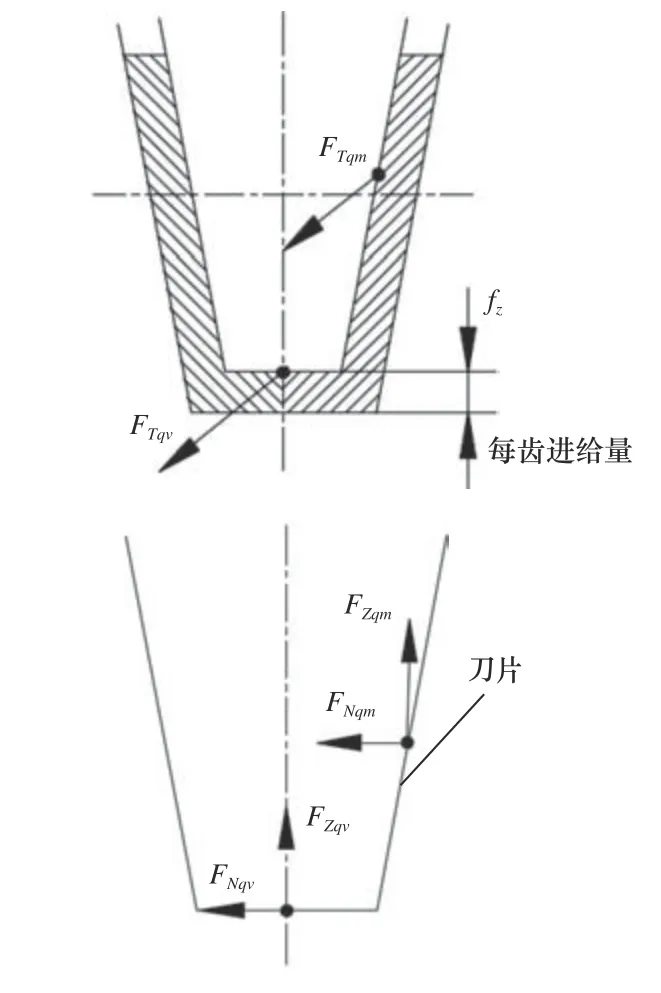
图8 刀片j 受力分布情况图

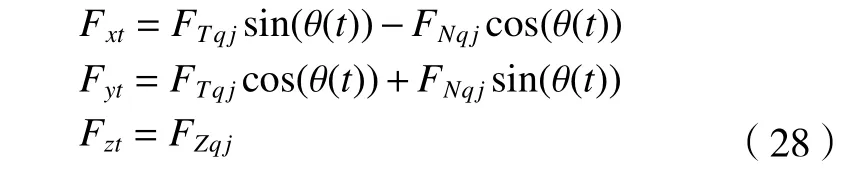
5 切削力程序编制及试验验证

5.1 切削力计算程序编制

为了得到成形法铣齿过程中，任意时刻t的切削力，使用Matlab 编程，对刀具上的切削力进行求解。其求解思想为，将齿槽沿着齿高方向进行分层，刀盘从第一圈开始进行循环，依次判断刀盘上每个刀齿是否参与切削。如果参与切削，则计算参与切削刀片主切削刃和顶刃的切削宽度和厚度，如果未参与切削，则进入下一个刀齿的计算，当刀盘上所有刀齿都判断完成后，跳出该层循环，刀盘进入下一圈，重新开始上述循环，直至完成一个齿槽的加工。

最后根据斜角切削理论和材料本构方程计算剪切应力τ，结合上述求解的瞬时切削面积，丛而对铣齿过程中3 个方向的瞬时切削力进行求解，其求解流程如图9 所示。

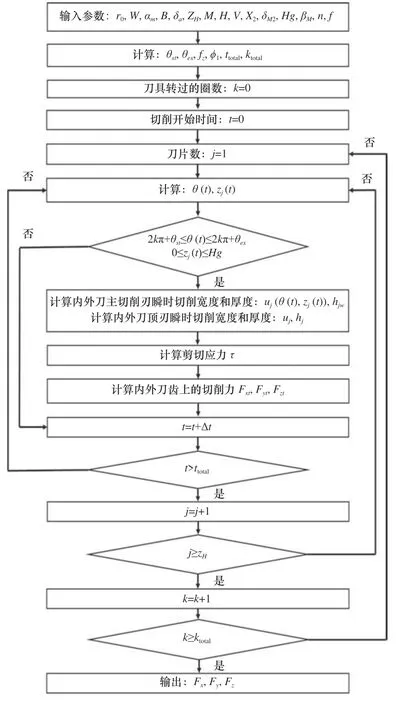
图9 切削力计算流程图

5.2 切削力试验验证

（1）切削力测量设备

本次实验由于测力仪装上后，导致机床限位，无法对标准大轮齿坯进行切削，选择在小齿坯上进行一次切削。使用小齿坯进行切削，只是对大轮齿坯几何参数、机床调整参数的数值进行了改变，但使用成形法加工所需的参数及加工原理并未发生变化，因此仍然可以使用该方法对成形法加工螺旋锥齿轮大轮的理论切削力模型进行验证。根据成形法加工原理，将刀具调整到切齿位置，保持齿坯位置和刀具的相对位置不变，进行一次切削。

实验所采用的机床为YKH2235 数控螺旋锥齿轮铣齿机。设备安装时，测力仪的一端与主轴连接，刀盘固定在测力仪的另一端，并在机床工装上安装相应的定子部分，如图10。当进行切削加工时，由于切削力的作用，测力仪内部的石英晶体（转子）会产生电信号，电信号通过定子与转子间的电磁感应，将信号传输给定子（如表1）。定子与电荷放大器相连，将传输来的电荷信号进行放大，再传输给数据采集系统，数据采集系统与计算机进行连接，在DynoWare 软件界面上实时显示被测切削力。

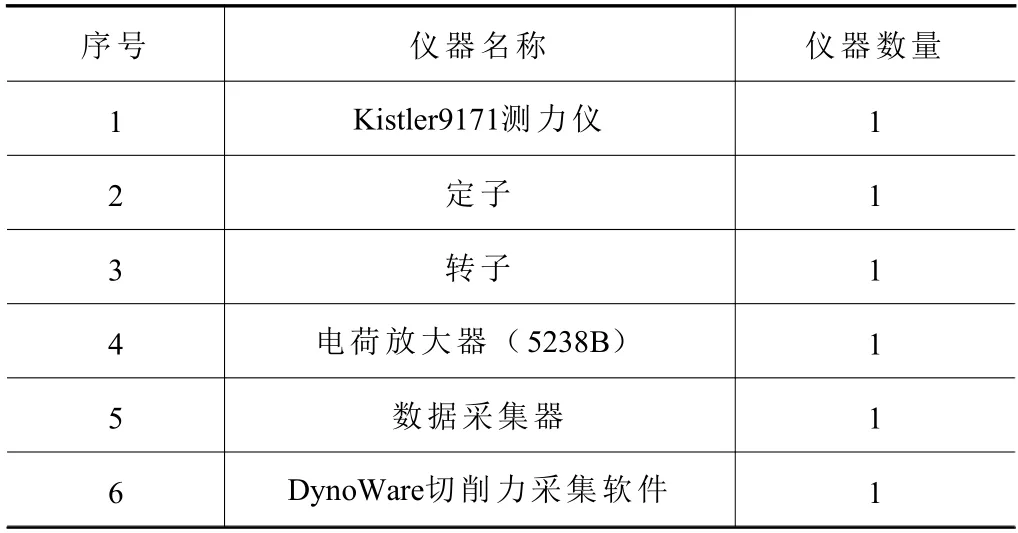
表1 切削力测量仪器

图10 切削力测量设备

（2）实验过程

为了保证实验结果的准确性，在刀盘安装在测力仪上面后，需要采用百分表检查主轴、测力仪和刀盘的同轴度，保证跳动误差小于0.01 mm。将测力仪外定子的信号传输线与电荷放大器连接，同时将电荷放大器与数据采集器相连，再通过USB 连接线与计算机进行连接。连接完成后，在测量前需要在DynoWare 采集软件中对数据采集过程进行相关参数设定。完成设定后，3 个方向铣削力采集量程为1 500 N；采集频率为 1 000 Hz；在机床主轴开始旋转时，点击开始记录，切削完成后点击结束。

（3）实验结果

实验中所选用的齿坯参数和铣刀盘主要参数如表2 所示。

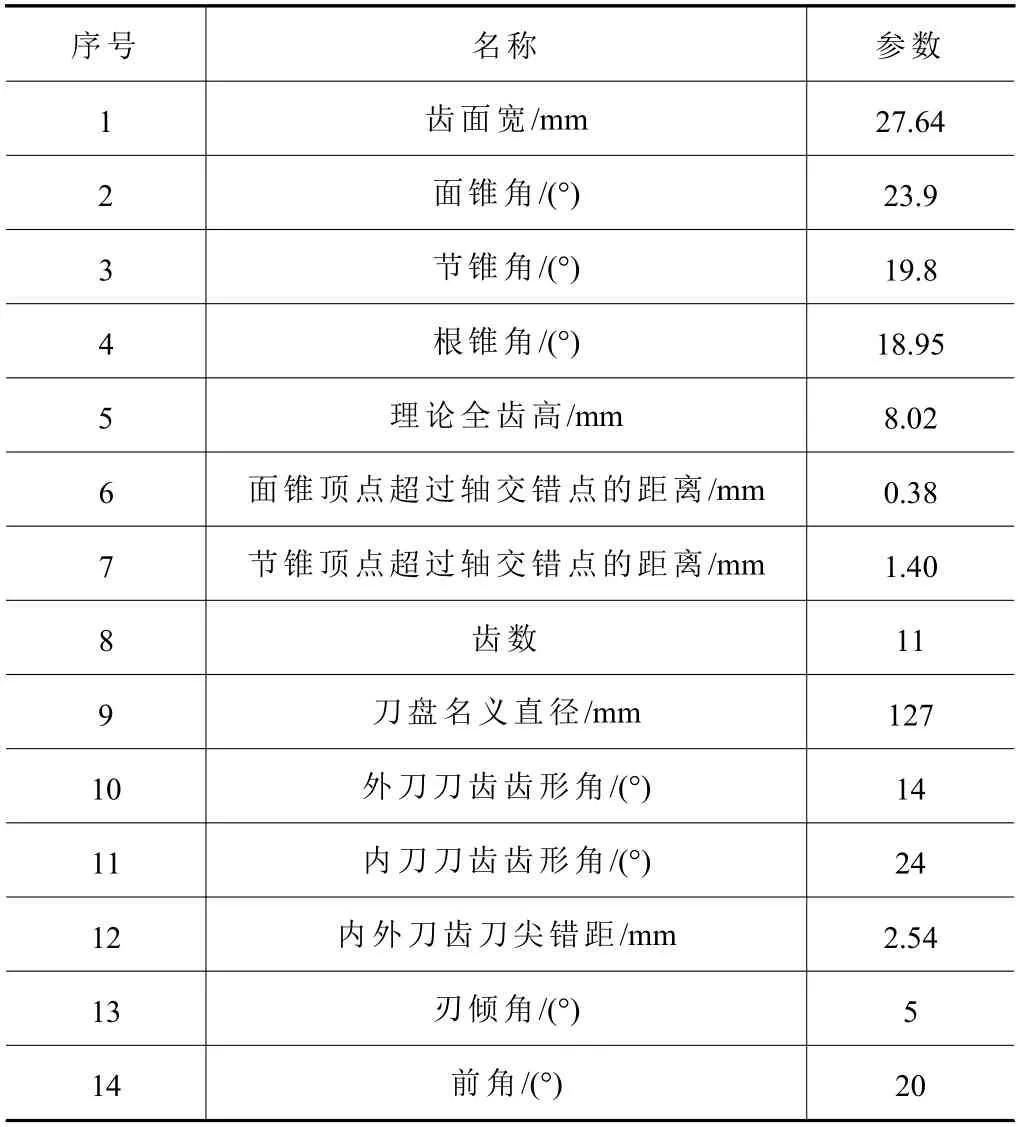
表2 成形法加工齿坯几何参数和铣刀盘参数

主轴转速为n=120 r/min，进给速度为20 mm/min的加工参数下，进行铣齿切削力的测量。其测量结果可在DynoWare 切削力采集软件中实时显示，其结果如图11 所示。

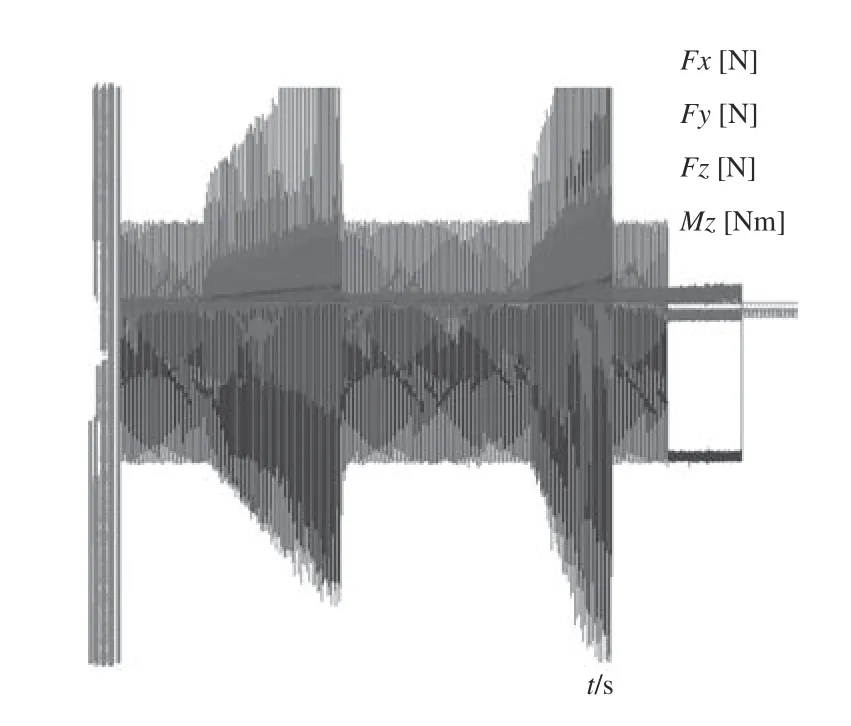
图11 铣齿切削力实测结果

从图11 中，可以发现在前段切削力平稳变化时，为主轴空转，其切削力数值依然在上下波动，其原因为测力仪和刀盘自重引起的，此时刀齿未切入工件。当切削力有一个变大趋势段，刀齿开始切入齿坯。在后期进行实验切削力数据处理时，会将测力仪和刀盘自重产生的切削力进行相应的减法运算，其中扭矩参数Mz不在单独考虑，因扭矩参数可转换为切削力数据。为了进一步对切削力数据进行分析，分别对X、Y、Z这3 个方向切削力数据导出，并截取其稳定切削时刻22.16～22.43 s 内的切削力数据。将其3 个方向切削力的实测数据与理论计算结果在同一图中进行绘制，如图12～14 所示。

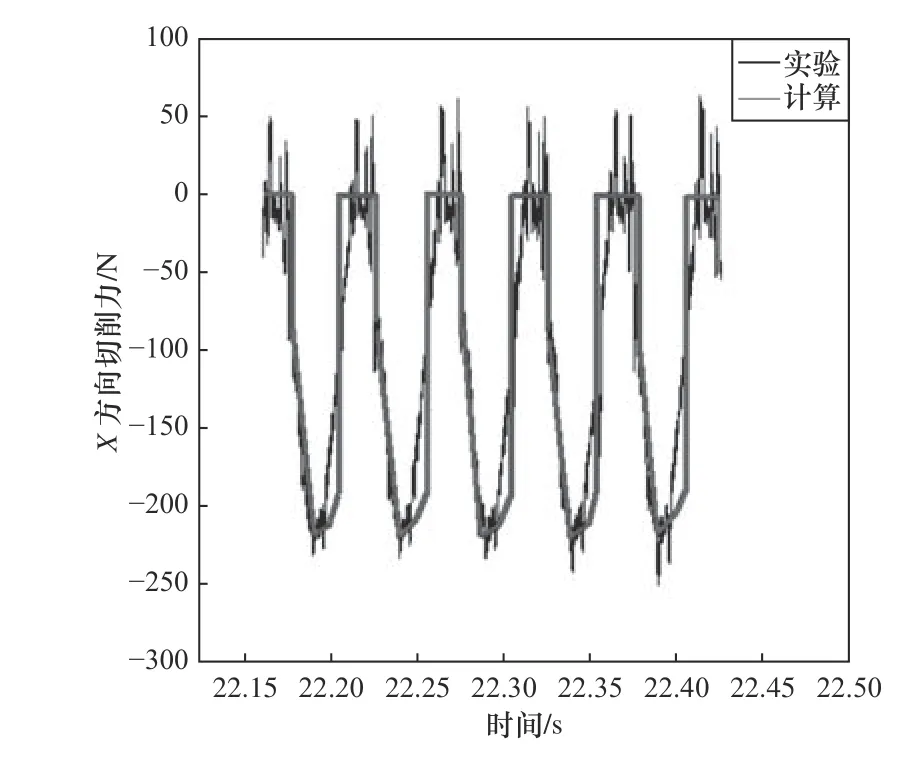
图12 X 方向切削力

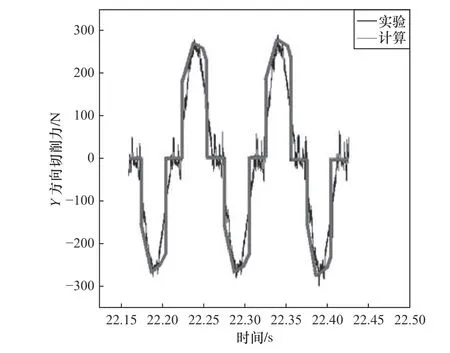
图13 Y 向切削力

从图14 中可以看出切削力理论计算结果与实验结果变化趋势基本一致，X、Y、Z方向刀齿切削力变化都是先增大后降低，即每个刀齿切入齿坯时，切削宽度先增大后减小；Y向切削力是随着方向交错变化的；Z向切削力中，力的幅值最小。统计每个波峰的实验和理论计算切削力最大值差值的绝对平均值，可以得出X方向切削力的相对误差为9.24%，Y方向切削力的相对误差为13.18%，Z方向切削力的相对误差为13.25%，各方向切削力的相对误差均在0～14% 的误差范围内，因此所建立的模型具有一定的精度。

图14 Z 向切削力

6 结语

（1）通过推导成形法加工螺旋锥齿轮过程中的瞬时未变形切削面积，结合齿坯材料剪切区应力计算结果，构建了成形法加工螺旋的切削力模型，并使用Matlab 编写了仿真计算程序。

（2）设计铣齿实验，对理论模型进行验证，经验证后发现，在X、Y、Z这3 个方向上切削力的理论计算结果和实验结果相对误差分别为9.24%、13.18%，13.25%。理论切削力模型计算结果和实验结果误差在14% 范围内，说明所建立的切削力模型具有较好的精度，为锥齿轮机床的设计，铣齿振动、刀具磨损研究等奠定了理论基础。