黄土地区某铁路专用线路基动力响应规律

交通强国战略的提出再次肯定了交通运输在国民经济发展中的重要驱动作用.铁路运输以其运量大、速度较快等特点在公共交通领域备受重视.长期以来，从业人员一直致力于改善路基服役性能，提升铁路运输的社会经济效益.列车运行荷载下路基动力响应研究涉及附加动应力分布及地表环境振动两方面主要内容，是路基工程设计、施工和减隔振的重要参考.

移动列车荷载引起的附加动应力分布规律是路基工程领域的重点关注内容.大量的现场测试、模型试验和数值模拟研究均表明：列车荷载作用下，路基内部动应力沿深度迅速衰减，动应力幅值随车速的提高而增大.相关研究结论是确定路基结构层厚度和填筑参数的主要依据.为了方便工程应用，《铁路路基设计规范》TB 10001—2016建议采用 Boussinesq 公式获取列车运行荷载下路基内部动应力分布，采用与车速相关的放大系数近似考虑荷载移动效果的影响.文献[6]考虑各结构层弹模对动应力分布的影响，采用Odemark理论计算路基内部动应力分布规律.

目前主流的两种动应力影响深度界定标准分别是“动应力幅值衰减至最大幅值的10%时对应的深度”和“动应力幅值沿深度分布曲线与1/10或1/5自重应力线交点的深度”.由于围压是影响路基土体力学和强度参数的重要因素，一般推荐采用动应力幅值曲线与自重应力线交点确定动应力影响深度.总体而言，附加动应力分布受路基土质条件、道床结构、车速和轴重等多重因素影响，衰减曲线大同小异，动应力影响深度普遍在3～6 m范围内.

目前的大量研究习惯针对具体工程背景评估列车运行诱发的环境振动对周边敏感建筑或区域的影响.孟庆成等基于现场测试和数值模拟评估了某火车站高架候车厅结构车致振动特性及振动对舒适度的影响.Yang等采用2.5D有限元方法研究了高速列车运行情况下空沟的隔振效果.Thompson等通过2.5D有限元方法研究了路基内部横向波阻块的减振效果及机制.Coulier等以西班牙El Realengo地区某铁路沿线场地为背景研究了混凝土灌注桩挡墙对地表环境振动的隔振效果.此外，Dijckmans等以瑞典Furet地区某铁路沿线场地为背景研究了波纹板桩板墙的隔振效果.Yarmohammadi等结合列车荷载激发环境振动的特点发展了一种耦合方法，研究指出双隔振沟的减振效果比单沟更好.马骙骙等通过开展宝兰高铁路堑段地面垂向振动现场测试研究了高速列车荷载下路堑的地面垂向振动随距离传播规律，指出场地速度特性(地基覆盖层与下卧层模量比、覆盖层厚度)是影响地面振动剧烈程度的重要因素.相比于动应力分布规律，环境振动研究涉及振动理论知识、情况各异的路基断面甚至精细化的地基-建筑物基础相互作用等问题，因此获得的量化成果相对较少.

在众多的铁路路基动力响应研究手段中，2.5D有限元方法因具备计算效率高、对复杂断面适应性好及理论基础完备等优点，在计算列车运行情况下路基动力响应方面独具优势.近年来其适用范围及应用场景不断扩展，在复杂路基环境振动规律、多相介质地基动力响应、路基临界速度预测等方面的应用屡见不鲜.

在高速铁路大量修建的政策背景下，铁路路基动力响应研究大多集中在我国东南沿海软土地区，黄土地区相关研究的系统性和深度均有所欠缺.由于黄土地区沟壑纵横，修筑铁路线路时大量采用填土路堤结构.阐述列车运行荷载引发的路堤-地基系统响应规律是细化设计参数、评估服役性能的重要举措.

徐州传统地方戏曲梆子戏在2008年被列为国家级非物质文化遗产，江苏梆子剧院有限公司（前身江苏省梆子剧团），现已实行企业化管理。梆子戏在徐州、河北地区目前仍继续上演，有一批固定观众。

本文依托某铁路专用线工程，旨在通过现场测试和2.5D有限元模拟揭示新建货运线路和临近既有客运线列车运行情况下路基动力响应规律，评估货运列车运行情况下路基动应力分布及影响深度，讨论线路附近办公区域的环境振动规律.以2.5D有限元为主要研究手段，辅以现场实测数据，在验证数值模拟精度的前提下开展参数分析.

1 现场测试概况

依托陕北黄土梁峁沟壑区某铁路专用线工程开展，测试断面位于洛河一级阶地，原始地基未经强夯处理.地层由上向下依次为黏质黄土(Ⅰ级非自重湿陷性黄土)及下覆基岩(页岩夹砂岩).黄土覆盖层厚度约10.0 m，地层分布较均匀，起伏变化较小.路堤中心填高10.8 m，边坡坡率1∶1.5.地下水位标高在路堤底面下部5 m处，年变化幅度在2 m左右.路堤主体采用压实黄土填筑，与既有线采用台阶搭接.

考虑到减少模板间的缝隙面，保证模板整体结构的稳定性，并尽量减小渗透。大坝上游背水面对应的模板规格为3m（宽）×3.5m（高），其中每三块模板组成一套。大坝下游的背水面对应的模板规格则为边长2.5m的正方形结构，从而形成双层翻升模板。基于提升模板刚度的目的，可以在模板顶面边缘部分增设修饰角钢护面。

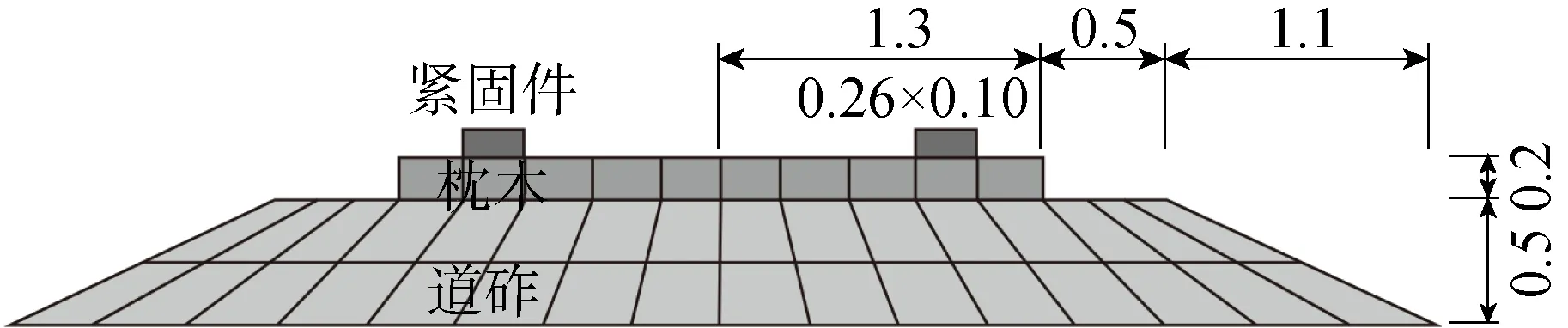
以图1现场测试断面为原型建立2.5D有限元模型，如图4所示.土体参数参照前期开展的相同工程背景下压实黄土动力参数研究及其他相似工程背景下的研究成果，如表1所示.需要指出的是，由于年代久远，既有线路堤设计参数无从考证，其分层情况及土体参数参照新建路堤设置.参照文献[20, 24]，有砟轨道系统(道砟-枕木-紧固件-铁轨)等效为坐落在基床表层的欧拉梁，抗弯刚度=13.254 MN·m，单位长度质量=540 kg/m. 列车轴重及运行速度与现场测试一致.

..轨道系统动力方程 将轨道系统模拟为欧拉梁，轮轴荷载作用下变换域内轨道的振动变形可以描述为

测试采用BY-1型电阻式双油腔动土压力盒，盘面尺寸20 cm，量程0.4 MPa.土压力盒盘面较薄，遇尖锐物体易损坏，因此并未在道床底面及基床表层范围内布设.数采仪器型号为DH5922N，采样频率 1 000 Hz.测试重载列车由1节车头及10节满载棚车组成，如图2所示.车头为东风4B型货运内燃机车，轴重23 t；棚车为P64K型，满载轴重为 22.5 t，测试车速30 km/h.

2 2.5D有限元模型验证及优化

2.1 2.5D有限元简介

列车运行荷载下图1中的4个测点处竖向动应力的变化规律如图5所示，图中=为空间长度.通过对比数值模拟结果和现场测试数据可知，二者波形一致，幅值近似.进一步从路基动应力响应角度验证了本文2.5D数值模拟方法在模拟列车运行情况下路基系统动力响应的可行性.

(1)

式中：为位移；为波数；为圆频率；i为虚数单位；上标“-”和“～”分别代表波数和频率变换.

..列车荷载 三维空间中沿轴移动的荷载可以表示为

设计方面的因素。主要有设计水平的高低、图纸质量的好坏等，具体表现为工程设计采用不成熟的技术方案，设计错误、遗漏或缺陷，图纸供应不及时、不配套或出错等。

“我压根儿没想到张仲平会当真。”左达说，“为了拿到这幢楼的拍卖推荐函，不下十家拍卖公司找过我，我跟他们开了同样的条件，你们公司是唯一当真的。”

(,,,)=(,)(-)()

(2)

式中：函数(,)表示荷载在与轴垂直断面上的分布特征；函数(-)表示荷载的移动特征，为荷载的移动速度；函数()表示荷载的时变特征.本文列车荷载在变换域中的表达式参照文献[20].

..地基系统动力方程 系统在变换域中的动力方程可表达为

(3)

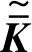
见面第一句话，他就对睁着一双疑虑大眼睛的女主人说，我有一个朋友叫老林，今晚我和他在一起。你放心吧，不会有事。我们说好的，互相帮忙。

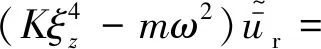
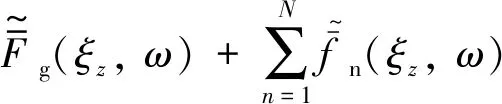
(4)

..道砟枕木紧固件各向异性单元建模信息 采用2.5D有限元方法计算有砟轨道路基动力响应时，习惯将道砟-枕木-紧固件-轨道系统等效为坐落在基床顶面的欧拉梁，在欧拉梁上作用沿横向均匀分布的列车荷载.采用欧拉梁等效时忽略了紧固件竖向刚度、枕木横向抗弯刚度和道砟体厚度等对荷载传递的影响.为了体现上述影响，已有文献通过各向异性单元考虑了紧固件和枕木对荷载竖向传递和横向分布的影响，但未考虑道砟各向异性的影响.本文建立图6所示道砟-枕木-紧固件各向异性实体单元，分析轨道系统建模方式对路基动力响应的影响.

在育肥猪日粮中组合使用益生菌与中药提取物复合物替代抗生素，提高生长性能效果显著，降低育肥猪背膘厚和提高瘦肉率，效果优于金霉素。

2.2 程序验证

采用MATLAB软件自编了2.5D有限元计算程序，为了验证其模拟效果，以瑞典国家铁路局(BANVERKET)在瑞典西海岸Ledsgard地区进行的X2000型列车运行现场实测数据为参照，通过本文2.5D有限元程序重现了两种车速情况下轨道位移随时间的变化规律.网格划分、地基分层及数据对比如图3所示.模型采用黏弹性人工边界作为吸收边界.可以看出，本文2.5D有限元程序可以较好地模拟列车运行情况下地基系统动力响应规律.限于篇幅， 列车、轨道系统及路基土体参数详见文献[16,18].

2.3 现场测试规律的数值重现

根据路堤填筑高程分层多次埋设土压力传感器，待路堤填筑完成且变形稳定后开展现场测试工作.路基断面轮廓、传感器分布及现场测试情况如图1所示.根据动应力分布规律及影响深度，在路堤中线处埋设4层土压力盒，最大埋深8 m.

从桌子上跳下来当然危险，但你阻止了他，他背着你跳，那更危险。所以该有个“训练策略”。把垫褥铺在地上，示范从椅子上跳下时身体应该保持怎样的姿势、两腿如何弯曲，起跳后身体、双腿和双手怎样配合行动，着地时身体、双腿和双手做怎样的动作。

2.5D有限元计算方法是基于路基断面(位于-平面)在列车运行方向保持不变的基本假定建立的.计算时首先采用双重傅里叶变换得到断面各节点在频率-波数域内的响应，然后由傅里叶反变换获得系统的实际响应.沿列车运行方向和时间的傅里叶变换可以表示为

即便如此，对比响应幅值随深度的变化规律可以看出，有限元计算获得的幅值衰减速度比现场测试数据慢.在2.5D数值模拟方面，目前针对其精度影响因素的争论主要集中在轨道系统抽象的合理性、路基土体的非线性及轮-轨相互作用等方面.在重现路基实际响应规律时，土体动力参数的代表性也会影响预测效果.相关研究指出，交通荷载作用下土体动力蠕变会带来额外的能量消耗.本文有意依据本次现场实测数据开展进一步研究，分析轨道系统建模方式和土体动力蠕变对路基动力响应的影响.相关研究指出，交通荷载下压实黄土的动应力-应变关系在一定起始应力范围内的非线性表现不明显.结合列车运行情况下路基内部动应力幅值分布情况，暂不考虑土体非线性的影响.

2.4 轨道系统各向异性实体建模对模拟结果的影响

文献[22]研究了交通荷载下路基填土的动力特性，从动力蠕变角度对土体的滞回特性进行了修正.研究指出土体动力蠕变会额外消耗能量，单个滞回中动力蠕变消耗的能量约等于塑性应变与静偏应力的乘积，如图10所示.图中：为应力，为应变，Δ为循环塑性应变.相比于塑性变形，单元的耗能特性是影响系统动力响应的直接因素，在动力数值分析中可通过调整阻尼比实现.因此，本文尝试通过提高单元阻尼比的方式间接讨论土体动力蠕变产生的额外能耗对路基动力响应的影响.轨道系统采用实体建模.

,rp=()

(5)

式中：为紧固件竖向刚度(取值为1.75×10N/m)；和分别为单元宽度和高度；为枕木间距(取0.6 m).

(6)

式中：为枕木混凝土弹性模量(为 12 500 MPa)；为枕木平均宽度(为0.25 m)；为材料密度(为 2 500 kg/m)；为材料泊松比(为0.2).

文献[26]基于大型三轴试验设备开展了道砟材料各向异性参数的试验.依据循环加载试验结果，道砟材料的9个各向异性参数取值分别为弹性模量,b=900 MPa，,b=,b=600 MPa；泊松比,b=0.31，,b=0.32，,b=0.28；切变模量,b=(,b+,b)/(2+2,b)=572 MPa，,b=(,b+,b)/(2+2,b)=455 MPa，,b=(,b+,b)/(2+2,b)=586 MPa.密度=1 900 kg/m，阻尼比=0.2.

..路基响应规律 分别提取图1所示测点动应力时程曲线(见图7)、动应力幅值横向分布(见图8)及竖向衰减规律(见图9)，讨论轨道系统建模方式对路基动力响应的影响.图中：为横向位置；为竖向深度；,amp为竖向动应力幅值.对比测点动应力时程曲线可知，轨道系统的实体化对路基动应力的影响体现在幅值上，实体化后动应力幅值减小，但是波形变化不明显， 循环应力的下限值也基本保持不变.

由图8可知，由于考虑了枕木的横向刚度，轨道系统实体化后浅层动应力幅值横向分布呈马鞍形，更符合路基动应力分布情况.采用欧拉梁模拟轨道系统时基床表层顶面动应力均匀分布且幅值及范围均偏大.由此导致动应力向下传递时影响范围和幅值偏大.可见在考虑了真实的荷载传递路径之后，道砟-枕木-紧固件的实体化建模使得路基内部动应力分布更为合理.轨道系统的过度抽象会导致路基内部动应力幅值和影响范围偏大.

“多谢神甫，当时收留我们。不然我们这样的女人，现在不知道给祸害成什么样了。”法比这时凑过来，不眨眼地看着玉墨。玉墨又说：“我们活着，反正就是给人祸害，也祸害别人。”她俏皮地飞了两个神甫一眼。

对比图9所示路堤中心线处动应力衰减规律可以看出，轨道系统实体化建模后路基内部动应力幅值与现场实测数据更加吻合.另外，本文实体化建模后单元数仅增加44个(共计 1 672 个)，可不考虑其对计算效率的影响.

2.5 土体动力蠕变能耗对路基动力响应的影响

参照已有文献，将轨道等效为欧拉梁，单根轨道抗弯刚度=6.4 MN·m，单位长度质量=60 kg/m.紧固件单元只考虑其竖向等效模量，其他方向的模量和单元质量设为一极小值.等效模量计算式为

动应力在路基中迅速衰减，因此对不同深度的土层采用差异化的附加阻尼比系数，为了充分体现动力蠕变的影响，设置基床表层、基床底层和路堤本体的附加系数分别为1.0、0.5及0.2.提取附加阻尼前后路堤内部动应力衰减规律如图11所示.

内筒采用管鞋超前设计。管鞋超前就意味着内筒最前端管鞋具有“吃入”地层的能力，否则将会影响整体钻进取心效率。因此，将以往取心钻具中的卡簧座进行优化设计，使其既能放置岩心卡取工具又能高效“吃入”地层。

低车速情况下附加阻尼对路基内部动力衰减无影响；高车速时阻尼比增加会轻微减小路基内部动应力幅值.已知40 m/s的车速远小于基床土体瑞雷波速(约130 m/s)，此时路基属于拟静力响应范畴，土体中并无波动传播，可能导致阻尼比对系统响应影响微弱.

当荷载移动速度大于地表瑞雷波速时会产生波动传播现象，路基由拟静力状态转换为动力响应状态.阻尼比的增大会强化路基材料对波动能量的吸收效果，从而减小动应力幅值.本文所涉工程背景不存在高速运行工况，因此在后续分析中不考虑附加阻尼的影响.

(1)通过分析关键词节点大小，可知在整个社会网络图谱中，创客教育处于中心位置，对整个网络图谱的作用最强。其次是创客、创客运动、创客空间等关键词，反映了当前研究热点。通过查询文献发现，研究主要集中在创客教育与创客、创客运动和创客空间之间的关系等方面。

河南自贸区于2017年正式挂牌成立，由于成立时间尚短，相对于其他发展成熟自贸区来说有关税收优惠政策相对不够成熟，但是由于我国自贸区已发展了一段时间，经验相对丰富，各种税收政策基本符合国际自贸区的相关税收惯例，发展相对完善，因此河南自贸区的进出口税收政策可以参照我国其他发展相对成熟自贸区的进出口税收政策。除了效仿其他自贸区相关进出口税收政策之外，河南省自贸区的税收优惠制度也可随着我国宏观政策的变化发生调整，以此来制定出更加适合河南省自贸区小微企业发展的税收优惠政策。

3 填方路基动力响应规律

基于上述分析，本文采用各向异性实体单元模拟轨道系统，在不考虑动力蠕变能耗的情况下讨论新建铁路和既有线列车运行时图4中的路基动力响应规律.左侧填方场地布置有设备间及办公、休息区域，因此重点关注新建线路路堤内部动应力分布及填方场地地表环境振动规律.

医药B2C平台顾客忠诚度模型，包括顾客、商品、平台网站三个方面的因素会对医药B2C平台顾客忠诚度产生正向的影响。如图1所示。

新建线路为货运线路，列车运行速度偏低，因此采用图2所示车辆模型，讨论车速较低情况下(10～40 m/s)，路基内部动应力分布及地表环境振动规律.由于缺乏车体动力学参数，暂不考虑轨道不平顺影响.既有线为客货共线铁路，采用常见的CRH3型车体参数，讨论列车在较高速度运行情况下引发的地表环境振动规律，同时评估轨道不平顺的影响.

3.1 新建线路列车运行情况下路基响应规律

提取不同车速下路基内部动应力分布规律，如图12所示.

可以看出，货运列车低速运行情况下，车速对路堤内部动应力分布的影响十分微弱.定义1/10自重应力线与动应力幅值分布曲线的交点所在深度为列车荷载的影响深度.参照《铁路路基设计规范》TB 10001—2016将道床等上部结构等效为14 kPa的均匀荷载，路基土重度统一取18.5 kN/m.本文工程背景下23 t轴重货运列车荷载对路基的影响深度约为4.2 m.

采用1/3倍频程中心频率的分频z振级表征列车荷载引发的环境振动，其表达式如下：

=20lg()+

(7)

式中：为该1/3倍频带振动加速度有效值；为加速度参考值(取10m/s)；为该1/3倍频带中心频率处的Z计权因子.

选取左侧地表与新建路堤中线水平距离约10、16、24及35 m的4个测点，获得40 m/s运行速度情况下各测点加速度频谱及分频z振级随1/3倍频中心频率变化，如图13所示.图中：为加速度幅值；为频率.可以看出，测点加速度响应集中在 0～4 Hz低频范围内.各测点分频z振级随中心频率变化规律类似.

为了分析列车运行情况下场地环境振动沿地表横向衰减规律，进一步提取地表节点最大分频z振级分布规律，如图14所示，图中为与线路垂直的水平横向地表位置.随着列车运行速度的提高，地表环境振动强度逐渐增大但衰减规律类似.行业标准《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》JGJ/T 170—2009规定4类区域(交通干线两侧区域)建筑物室内振动限值为昼间75 dB、夜间72 dB.当前工况下距离路基中心线15 m以外设备间及办公区域的最大分频振级基本不超过72 dB.货运线路车速一般较低，以往研究重点关注轴重对路基响应的影响，以至于本文所涉货运内燃机车及棚车车体动力学参数十分鲜见，因此本文暂不考虑新建线路轨道不平顺对环境振动的影响.

3.2 既有线列车运行引发的地表环境振动规律

本文仅考虑客运列车以较高车速(40～80 m/s)运行时引发的环境振动规律，车型采用常见的CRH3型客运列车，其轴重及轮对相对位置详见文献[20].不同车速情况下路基表面最大分频z振级分布如图15所示.可以看出，当列车以80 m/s的速度运行时激发的办公区域地表环境振动基本满足要求.环境振动随测点与加载位置距离的增大近似呈线性衰减的趋势.另外，最大分频z振级曲线在新建路堤区域有轻微“上扬”.对比图14也可以看出，环境振动曲线在经过既有线时有类似“上扬”趋势.上述现象表明模量较大的地表凸起可能会减缓竖向环境振动的衰减.

其四,药品剂量会导致处方治疗效果具有严重变化,很多中药调配工作人员经常会犯一些常规性的错误,就是根据自身感觉调配药物,没有经过严格的标准进行,导致配制的药品剂量无法精准,从而影响临床治疗效果,比如红花药材,小剂量的红花具有显著的养血作用,大剂量则会导致患者发生破血情况发生,还有肉桂,小剂量能够有效的引火归原,而大量的肉桂则具有祛寒止痛的功效[5]。另外在实际配置过程当中,需要严格注意药物剂量以及药物的毒性含量,避免剂量过多导致患者发生中毒情况,在本次研究当中药品剂量问题占总比的30%。

列车在竖向不平顺的轨道上运行时，车体会发生振动从而导致轮轨接触力的改变.一般车速越高不平顺对轮轨力的影响越大.在研究客运列车高速运行诱发的铁路路基动力响应规律时不宜忽略轨道不平顺的影响.本文参考德国高速铁路高低不平顺谱，根据其界定的波长-波高对应关系设定3种不平顺参数(参数I～III 的波长分别为2、10、50 m，波高分别为0.15、0.6、2.4 mm)初步评估轨道不平顺对环境振动的影响.10自由度车体参数及轨道不平顺在2.5D有限元中的实现详见文献[28].

考虑轨道不平顺时，既有线列车运行情况下路基环境振动规律如图16所示.对比平顺情况下的响应可以看出，当客运列车以常规车速(40 m/s)行驶时，不平顺波长越大，轨道不平顺对环境振动的影响越小.在空间上，随着与加载点距离的增大，不平顺对环境振动的影响逐渐显现，并且存在分叉现象.波长越大，最大分频z振级曲线的分叉点距离加载点越远.其原因可能是不平顺荷载会激发地基内部波动传播，使得不平顺荷载产生的附加响应在路基内的衰减规律与平顺荷载产生的响应衰减规律产生差异，加之式(3)对数取值会放大远场微小的响应差异，由此产生了明显的分叉现象.上述现象表明改善轨道短波不平顺可以有效控制列车运行诱发的环境振动.

观察车速较高时(80 m/s)的环境振动规律可以看出，轨道不平顺对环境振动的影响减弱.由于本文既有线为非高速铁路线路，所以对此工况不做过多讨论.

4 结论

本文以黄土地区某铁路专用线工程为背景，通过现场测试得到了填方路堤内部的动应力响应规律，据此验证了2.5D有限元数值模拟精度并探讨了轨道系统各向异性实体化建模及土体动力蠕变对模型动力响应的影响.在此基础上，分别讨论了新建线路运行货运列车及既有线运行客运列车情况下路基动力响应规律，得出以下几点结论.

(1) 轨道系统的过度抽象会导致路基内部动应力幅值和影响范围偏大.由于考虑了真实的荷载传递路径，道砟-枕木-紧固件系统的各向异性实体化建模使得路基内部动应力分布更为合理.

(2) 路基处于拟静力响应状态时动力蠕变引发的能量消耗对路基动应力衰减规律的影响可以忽略，路基处于动力响应状态时动力蠕变引发的能量消耗会减缓路基内部动应力的衰减.

(3) 23 t轴重货运列车低速运行时，车速对黄土填方路堤内部动应力分布影响微弱，动应力影响深度约为4.2 m.

(4) 随着地表测点与加载位置间距的增大，轨道不平顺对场地环境振动的影响逐渐显现.车速越低轨道不平顺对场地环境振动的影响越明显.改善轨道短波不平顺是控制环境振动的有效措施.