考虑概率电压不平衡度越限风险的共享储能优化运行方法

随着化石资源的不断减少和生态环境的持续恶化，大力发展可再生能源发电已成为全球各国的共识.在“碳达峰、碳中和”目标的引领下，未来我国可再生能源渗透率将进一步提高.在配电网三相不平衡负荷影响的基础上，可再生能源分布式接入将进一步提高配电网的电压不平衡越限风险.与此同时，可再生能源发电的间歇性和随机性特征也将给配电网的安全运行带来巨大挑战，增加了配电网电压不平衡的监控和评估难度.在此背景下，研究可再生能源发电不确定性对配电网电压不平衡越限风险的影响及应对措施具有重要价值.

两个人都在气头上，父母也不好多劝，过了两天，等田朵的一股怨气、小宁的半腔怒火都消了消之后，双方父母才话里话外地劝合。小宁看这两天田朵忙前忙后的，也就不再提离婚这茬了。其实，回头想想，他们之间并不存在不可调和的矛盾，说到底，就是挤牙膏、吃醋那点破事，和漫长的、珍贵的婚姻之路相比，这些小瑕疵，根本不值一提。

收集2015年1月~2015年12月来我院口腔科门诊就诊的粘液腺囊肿病人260例,男116例,女144例,年龄16~50岁,囊肿直径0.5—2.0 cm,其中上下唇105例,舌部155例。所有病例均为首次出现的粘液腺囊肿。

电压不平衡是指三相电压的幅值不同或相位差不是120°.配电网中的电压不平衡不仅会增大网络损耗及降低电能质量，还会引起系统设备及终端用户设备的过热现象，从而加速设备的热老化，缩短设备使用寿命.同时，电压不平衡问题已成为制约配电网中可再生能源渗透率提高的关键因素.文献[10]指出，随着单相可再生能源接入的不断增长，马来西亚国内部分配电网电压不平衡度将超过其容许阈值(1%)，成为该国提高可再生能源渗透率的关键障碍.此外，文献[11-12]研究了欧洲等配电网中基于电压不平衡度容许阈值的最大允许并网分布式光伏数量.

研究如何降低电压不平衡越限风险对于提升配电网的运行水平和可再生能源的消纳量都具有重要意义.近年来，计及可再生能源发电的不确定性，国内外学者通过概率分析方法对配电网的电压不平衡进行了研究.文献[13-14]利用蒙特卡洛模拟(Monte Carlo Simulation，MCS)方法对分布式光伏发电装置造成的配电网电压不平衡问题进行了概率风险评估.文献[6]研究了分布式风机接入对配电网电压不平衡的影响.文献[8]依据配电网历史监测数据，采用MCS方法获得了配电网电压不平衡概率信息.上述研究均采用了配电网三相概率潮流(Probabilistic Power Flow，PPF)算法获得电压不平衡概率信息，但所得概率分析结果缺乏实用性，不能用于指导实施电压不平衡越限风险的具体应对措施.

在批次为720,学习率为0.03的实验条件下,对网络输入步长问题进行实验,以RMSE作为评价指标,实验结果如表2所示。

式中：为风速；和分别为Weibull分布的形状参数和尺度参数.

1 配电网概率电压不平衡度越限风险指标

1.1 可再生能源不确定性建模

对于含分布式可再生能源的配电网，间歇性可再生能源发电(风电、光伏发电)是影响其运行的主要不确定性因素.风机、光伏出力分别与风速、光照强度密切相关，在长时间尺度下，风速近似服从Weibull分布，光照强度近似服从Beta分布.Weibull分布和Beta分布的概率密度函数分别如下所示.

小说主人公斯库特在经历与老师同学冲突，莫迪小姐房子失火，汤姆被指控案以及万圣节夜遇袭后，在她父亲、保姆、伙伴、邻居，亲戚等引路人的呵护和指引下逐渐成长成熟起来。本文从正反两方面来探讨成长路上引路人角色的重要作用。

Weibull分布的概率密度函数：

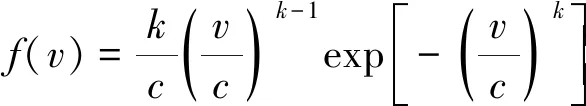
(1)

针对上述问题，本文提出了基于全局灵敏度分析(Global Sensitivity Analysis，GSA)的共享ESD配置策略与优化运行方法.首先，建立了配电网概率电压不平衡度计算模型，提出了基于反向传播神经网络(Back Propagation Neural Network，BPNN)的代理模型，用以克服传统MCS方法计算效率低下的问题，并定义了配电网概率电压不平衡度越限风险指标.然后，提出了基于Wasserstein距离的全局灵敏度分析方法，用于量化可再生能源随机出力对配电网电压不平衡的影响，辨识关键的可再生能源机组，指导共享ESD的配置.最后，提出了考虑配电网概率电压不平衡度越限风险的多时段共享ESD配置策略与滚动预测优化运行方法，降低配电网概率电压不平衡度的越限风险指标.通过对IEEE 123节点配电网系统的仿真分析，验证了所提方法的有效性.

目前，配置储能装置(Energy Storage Device，ESD)是降低配电网电压不平衡越限风险的有效途径.文献[9]采用单相ESD降低了高渗透率光伏集成配电网的电压不平衡越限风险.文献[15]通过采用社区ESD及充放电控制策略，降低了负载与单相光伏设备造成的配电网电压不平衡越限风险.文献[16]基于ESD的最优控制策略，有效降低了可再生能源发电导致的配电网电压不平衡越限风险.然而，ESD的投资成本高，投资回报周期长，为了进一步提高ESD的经济效益，越来越多的国内外学者开始关注共享储能的研究.与常规的配套储能不同，共享储能可为多个可再生能源机组提供充、放电服务，增强配电网消纳可再生能源的能力.文献[19]采用共享ESD并基于分布式优化算法提高了分布式可再生能源发电的利用率.文献[20]通过共享ESD抑制分布式可再生能源的出力波动，提高了用户收益.文献[21]联合使用共享ESD与需求侧资源，通过跟踪可再生能源发电曲线，增加了可再生能源的消纳.考虑可再生能源发电不确定性，利用共享ESD降低配电网电压不平衡越限风险时，需要研究一种合理有效的共享储能配置策略与优化运行方法，从而提高配电网运行的安全性与经济性.

Beta分布的概率密度函数：

服装面料再造设计的主要灵感就是大自然当中的自然万物，设计师可以在动植物、山川河流、日月星辰等方面获得设计灵感。因此设计师在服装面料再造设计过程中可以在自然界寻找灵感，探索大自然的奇妙之处，将大自然的团运用到服装面料再造设计当中，使整体服装呈现出特别的魅力。

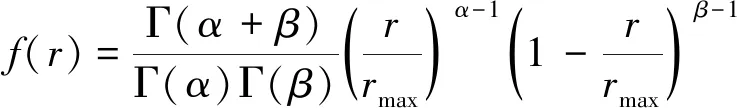
(2)

式中：和分别为光照强度和最大光照强度；、为Beta分布的形状参数；Γ(·)为伽马函数.

对于风电机组，给定切入风速、额定风速及切出风速，风电机组有功出力与风速的函数关系可表示如下：

(3)

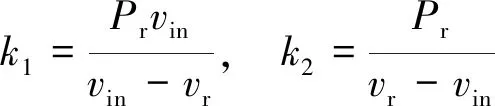
(4)

式中：为风电机组的额定有功功率；、为系数.

本文假定风机运行期间的功率因数保持不变，则其无功功率为

=tan

(5)

对于光伏电池(本文不考虑光伏电池输出的无功功率)，给定光伏电池的光电转化效率及光伏阵列总面积与光伏电池输出的有功功率的关系可表示如下：

=

(6)

由于配电网中的可再生能源机组所在地理位置相近，其天气条件(风速、光照强度)具有一定的空间相关性.同时，在相邻时间节点同一位置的天气条件数据也具有一定的时间相关性，本文采用线性相关系数矩阵表征随机变量间的时空相关性.

1.2 概率电压不平衡度定义

电压不平衡度(Voltage Unbalance Factor，VUF)用于描述电力系统中三相不平衡的程度，是量化电压不平衡程度使用最广泛的指标，定义为

(7)

式中：为正序电压；为负序电压.正序电压与负序电压可通过三相不平衡线路的线电压计算得到：

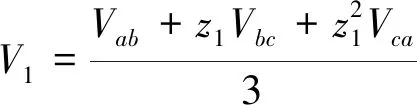
(8)

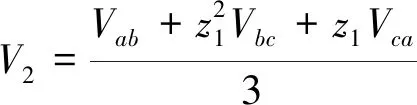
(9)

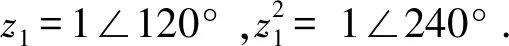
考虑可再生能源发电不确定性的影响，配电网内各节点的VUF将具有一定的概率特性.为表征VUF的概率特性，本文提出概率电压不平衡度(Probabilistic VUF，PVUF)指标：

=(()()())=

()

(10)

式中：为可再生能源随机出力；(·)表示式(7)～(9)的计算过程；(·)表示配电网三相概率潮流计算过程.

PVUF可用于量化可再生能源出力不确定性经不确定性传播过程后对配电网电压不平衡度的影响，并以PVUF的统计特征量(均值、方差、概率密度函数等)为表征.结合式(10)，基于可再生能源不确定性模型，利用Nataf变换和MCS方法可实现配电网各节点的PVUF指标计算.根据《电能质量 三相电压不平衡》(GB/T 15543—2008)规定，电力系统在正常运行状态下，公共连接点的VUF数值大小不得超过2%，短时不得超过4%.通过计算PVUF指标，可获得可再生能源随机出力影响下配电网节点电压不平衡度超过容许阈值的概率，从而为运行者采取有效手段降低电压不平衡越限风险提供参考.

1.3 基于BPNN的PVUF计算

基于MCS方法的PVUF指标计算虽然能得到精确度较高的结果，但该方法依赖于大规模的随机采样与运算，计算效率低下.为了解决这一问题，本文引入BPNN作为代理模型，以代替VUF计算的原始模型，提高PVUF指标的计算效率.

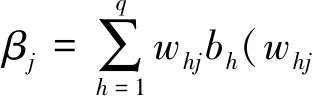
利用BPNN构建代理模型以表征配电网随机输入变量(可再生能源随机出力)与VUF指标间的非线性关系，通过代理模型替代原始模型计算，降低大规模随机取样后PVUF指标的计算时间，显著提高配电网PVUF指标的计算效率.图2给出了基于BPNN的配电网PVUF指标计算流程.

④治疗性诊断。过去多数学者对该病诊断性神经阻滞方法是:在颈部第二横突尖部给予消炎镇痛药做试验性治疗,若注射后疼痛迅速缓解,或消失,有助于确立诊断。

股票市场之间的相依性[注]参考Patton(2006)，本文所指的相依性(Dependence)包括变量间任何线性与非线性关系，而一般的Pearson相关性(Correlation)仅指变量间的线性关系。在资本风险管理中发挥着重要作用。当股票市场完全分割时，风险不可能在各个市场间传递，从而避免了来自外界的冲击，这也是中国在1997—1998年的亚洲金融危机中能够幸免的原因(洪永淼等，2004)。而当股票市场之间存在较强的相依性时，风险就会在各个市场溢出，在经济动荡或经济危机期间，股票市场之间的相依性会表现得更强。

1.4 PVUF越限风险指标

本文采用PVUF越限概率作为越限风险指标，通过计算配电网系统严重电压不平衡事件发生的概率，量化评估配电网系统的电压不平衡风险水平.PVUF越限概率即配电网节点PVUF超过容许阈值的概率，则节点的PVUF越限风险指标为

==1-(VUF≤)

(11)

式中：为节点的PVUF越限概率；VUF为节点的PVUF指标；为配电网节点PVUF的容许阈值；(VUF≤)为节点的PVUF指标不超过容许阈值的概率.

2 基于全局灵敏度指标的共享储能装置配置策略

针对可再生能源发电不确定性对配电网节点电压不平衡度的影响，本文提出基于全局灵敏度指标的共享ESD配置策略，通过全局灵敏度分析方法，量化可再生能源发电对配电网节点电压不平衡度的影响，从而为共享ESD提供最佳的配置点.

2.1 基于Wasserstein距离的全局灵敏度分析方法

灵敏度分析能够定性或定量地评估系统输入对输出的影响，准确辨识影响系统运行状态的关键输入变量.灵敏度分析方法主要包括局部灵敏度分析(Local Sensitivity Analysis，LSA)与全局灵敏度分析.相较于LSA方法，GSA方法能够同时考虑多个输入变量或输入变量间相互作用对系统输出的影响，可适用于系统随机输入变量波动范围较大的场景.目前，考虑可再生能源发电不确定性，GSA方法在含随机源-荷的潮流分析、小干扰稳定分析等领域已有应用.

常用的全局灵敏度分析方法包括Sobol’法与Borgonovo指标法.Sobol’法基于输出样本的方差信息计算全局灵敏度指标，但是方差作为输出变量的一种统计矩，无法表征输出变量的概率分布信息.并且，Sobol’法要求输入变量为独立变量，未能考虑输入变量间的相关性.Borgonovo指标法基于输出样本的概率密度函数(Probability Density Function，PDF)计算全局灵敏度指标，充分考虑了输出样本的概率信息，然而其求解需要利用MCS与双循环过程，计算规模庞大，计算效率低.同时，PDF的估计问题本身是一个不适定的计算问题，准确地估计PDF有一定难度.

针对上述问题，本文提出基于Wasserstein距离的GSA方法，通过量化PVUF有条件概率分布与无条件概率分布间的平均差异，从而辨识对配电网电压不平衡度具有显著影响的关键可再生能源随机出力.该方法基于输出样本的累积分布函数(Cumulative Distribution Function，CDF)计算全局灵敏度指标，能充分考虑输出样本的概率特征，由于不使用统计矩信息(均值、方差等)，对输入变量的独立或相关性也没有限制.同时，与PDF相比，准确地估计CDF更为简单.首先，利用Wasserstein距离量化不同概率分布间的差异性，令变量和分别服从概率分布和，则和之间的-Wasserstein距离为

(,)=

吸收式热泵技术在地热供暖中的应用………………………………………………………………………………周航兵（3.27）

(12)

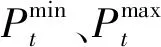
当、为一维变量时，概率分布和的-Wasserstein距离可简便计算，如下式：

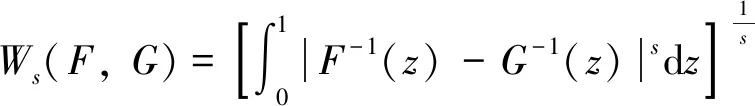
(13)

式中：为概率分布函数逆函数积分时的自变量.

设维随机输入变量为= […]，系统输出响应为，为了定量评估第个随机输入变量对系统输出响应的影响，定义基于Wasserstein距离的全局灵敏度指标如下：

(14)

式中：()为随机输入变量的PDF；为输出变量的无条件概率分布，即维随机输入变量均随机变化时的概率分布；∣=为输出变量的有条件概率分布，即随机输入变量取固定值、其他随机输入变量,, …,-1,+1…,均随机变化时的概率分布；(,∣=)表示的无条件概率分布与有条件概率分布间的-Wasserstein距离.

为简化全局灵敏度指标的计算，可将式(14)的积分形式转换为下式：

船舶减速临界关系见图2。将相邻船舶的2个通航状态标绘在线段上，通过简化船舶减速过程描述来构建减速边界条件。图2中初始状态为船舶S2进入航道的时刻，其前方船舶S1匀速行驶在航道内，两船的初始间距为d0，船舶S1、S2的速度分别为v1、v2。在船舶速度关系为v2>v1的前提条件下，船舶S2与船舶S1间距离逐渐减小。图2中最终状态为船舶S1即将驶出航道的时刻，两船间的距离为d1。

(15)

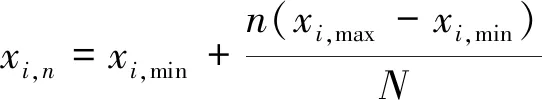
(16)

式中：为对取值区间的等分段数；,max、,min分别为随机输入变量可取的最大值与最小值取值越大，计算结果越准确.

一部地理科学史，就是一部地理科学家们的奋斗史。教材通过介绍古今中外地理学家不畏艰难、执着奋斗所作出的重大贡献，或讲述科学理论的形成和发展过程，以潜移默化地培养学生追求真理的精神。教材中对地理科学史人物的介绍，不能停留于素材表面，而应挖掘其教育内涵。如学习“马寅初和他的《新人口论》”专栏时，不仅要介绍马寅初是新中国提出控制人口数量第一人的时代意义、《新人口论》的学术价值，更要通过他的正确思想遭到错误批判但仍坚持真理并最终得到平反昭雪的事例，对学生进行科学观教育，培养学生坚持真理的科学精神。

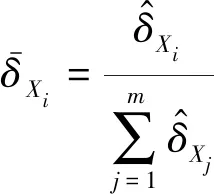
(17)

2.2 多时段共享储能配置策略

基于全局灵敏度指标辨识关键可再生能源发电机组的位置后，本文采用ESD降低配电网的电压不平衡越限风险.通过ESD的充、放电过程，实现可再生能源发电高峰与低谷时期的电能互补，平抑可再生能源出力波动，降低由于可再生能源发电波动性造成的配电网电压不平衡越限风险.本文考虑到ESD建设的经济性，假定配电网内采用共享的ESD为可再生能源机组服务，即一个共享ESD可选择为多个可再生能源机组提供波动平抑，但同一时间一个共享ESD只能配置于一个可再生能源机组处.为最大程度地发挥共享ESD的应用效果，本文提出基于GSA的共享ESD配置策略：① 计算各个可再生能源机组出力对PVUF的全局灵敏度指标，将全局灵敏度指标从大到小排列获得可再生能源机组的重要性排序结果，辨识对PVUF具有显著影响的关键可再生能源机组；② 将关键可再生能源机组接入点作为共享ESD的配置点，以充分发挥共享ESD的应用效果，降低配电网的三相电压不平衡越限风险.

可再生能源机组出力受风速、光照强度等天气条件影响显著，不同时段下，需要根据可再生能源出力波动情况不断调整共享ESD装置的配置点.本文将一天分为多个时段，按照所提共享ESD装置的配置策略，针对各时段可再生能源机组出力特征，在每个时段都给出一个ESD配置方案，最终形成多时段共享储能配置策略.

3 考虑配电网概率电压不平衡度越限风险的共享储能装置优化运行方法

在实现多时段共享ESD配置的基础上，本文提出基于滚动预测优化的ESD优化运行方法，通过平抑可再生能源出力波动，最大限度地降低可再生能源随机出力导致的配电网电压不平衡越限风险.

3.1 基于滚动预测优化的共享ESD优化运行方法

本文所提出的共享ESD优化运行方法实质是通过调控ESD的充电、放电过程，使得当前时段的可再生能源与ESD联合出力波动性最小.在实际应用时，该方法需要基于可再生能源出力的预测数据与历史数据，计算ESD的最优充/放电功率.所提滚动预测优化方法通过不断增加当前时刻的量测数据，滚动更新可再生能源出力的预测数据与ESD的最优充/放电功率.如图3所示，图中为运行方案，在完成多时段共享储能的配置后，每个时段含个时刻可实时测量可再生能源出力，更新ESD充/放电功率值.

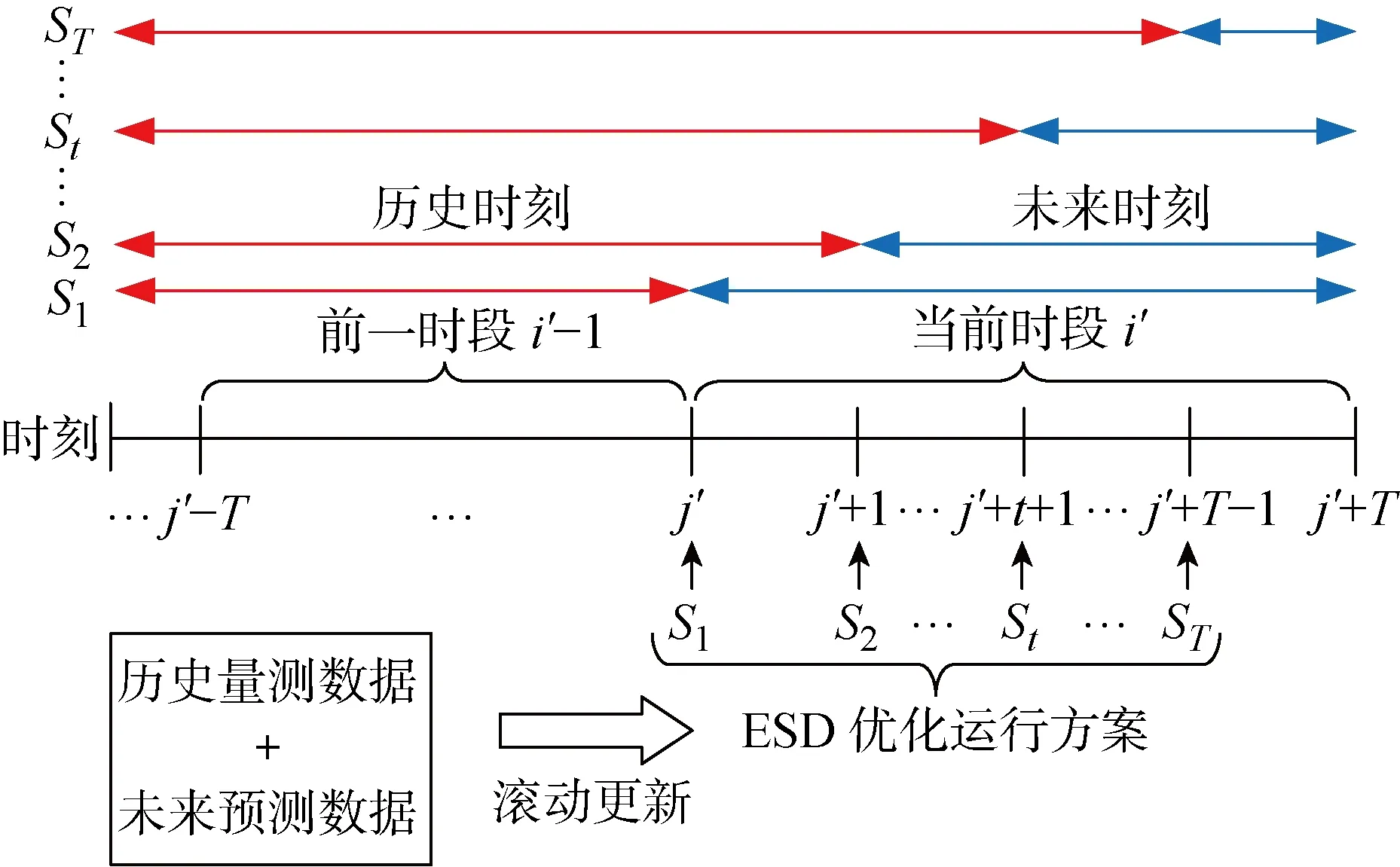
结合图3，进一步给出基于滚动预测优化的共享ESD优化运行方法的具体步骤.

获取配电网基本信息，根据全局灵敏度指标确定当前时段′的共享ESD配置方案.

利用当前时段′初始时刻′之前的可再生能源出力历史量测数据，预测得到未来时刻可再生能源出力数据；结合历史量测与未来预测数据，计算得到初始的共享ESD运行方案，即共享ESD在当前时段′各个时刻(时刻′到时刻′+-1)的最优充/放电功率，并将方案中当前时刻′的共享ESD最优充/放电功率作为其实际运行结果.

在当前时段′第′+时刻(= 1, 2, …,-1)，将实时测量得到的′+时刻可再生能源出力加入历史量测数据中，对未来时刻可再生能源出力预测值进行校正，重新获得未来预测数据；结合新的历史量测与未来预测数据，计算当前时段′第′+时刻共享ESD的运行方案S+1，将方案S+1中当前时刻′+的最优充/放电功率作为其实际运行结果.

完成当前时段′运行结果计算，确定时段′+1的共享ESD配置方案，并重复步骤2、3.

通过所提滚动预测优化方法，后一时刻用于计算共享ESD最优充/放电功率的数据总是比前一时刻的数据精确，因此滚动更新优化能够保证共享ESD的运行方案更安全可靠.同时，该方法能够降低预测误差对共享ESD实际运行效果的影响，提升共享ESD降低配电网电压不平衡越限风险的效果.

3.2 共享ESD优化运行模型

结合可再生能源出力的预测数据与历史数据，应用共享ESD优化运行模型可获得ESD在当前时段各个时刻的最优充/放电功率.为降低可再生能源发电波动性的影响，本文利用当前时段可再生能源与共享ESD联合出力的方差来表征功率波动性，并以波动性平抑为优化目标(即最小化该方差值).在时刻(= 1, 2, …,)时，共享ESD滚动优化的目标函数如下：

()=

(18)

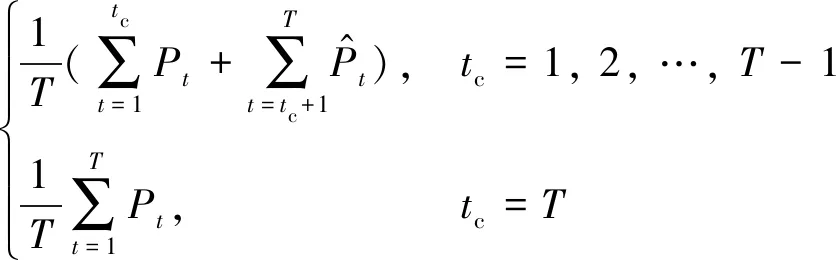
(19)

在上述目标函数下，决策变量为共享ESD的充/放电状态与充/放电功率.约束条件如下:

(29)

式中：(,)为变量和所有可能的联合概率分布集合，其边缘分布为和；、为利用联合概率分布所获得的样本；(,)为距离函数，通常令(,) = ‖-‖；为阶数，实际应用中一般取1或2.

约束条件包括共享ESD充/放电功率、可再生能源与共享ESD联合出力、共享ESD的荷电状态的最大和最小值限制，见式(20)～(24).同时，需要计算可再生能源与共享ESD的联合出力、共享ESD的SOC，见式(25)～(28)，并确保共享ESD不会同时处于充电与放电状态，见式(29).

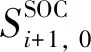
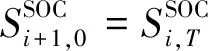
(30)

综上所述，考虑配电网概率电压不平衡度越限风险的共享ESD配置与优化运行流程如图4所示.

4 算例分析

4.1 算例系统

本文采用含分布式可再生能源机组的IEEE 123节点配电网进行仿真测试.配电网中3个风电机组和2个光伏电池的参数分别如表1、2所示，系统拓扑图如图5所示，其中，WT表示风电机组，PV表示光伏电池，S表示开关.根据历史数据拟合得到风速与光照强度的随机分布参数，并分别利用Weibull分布与Beta分布生成所需的风速与光照强度数据样本，采用线性相关系数刻画风速、光照强度之间的相关性.将配电网一天24 h的运行时间分成4个共享ESD配置时段，每个配置时段包含6个运行时刻.该配电网系统中安装有2个共享ESD，其参数如表3所示，在每个配置时段单个共享ESD只能为1个可再生能源机组提供服务，即连接共享ESD与可再生能源机组的多个开关在每个配置时段只有1个开关处于闭合状态.本文仿真环境为Intel Core i7-10 700 八核CPU，16 GB内存，使用MATLAB R2020b编译和测试.

将式(15)所得全局灵敏度指标归一化处理，获得最终的全局灵敏度指标计算结果：

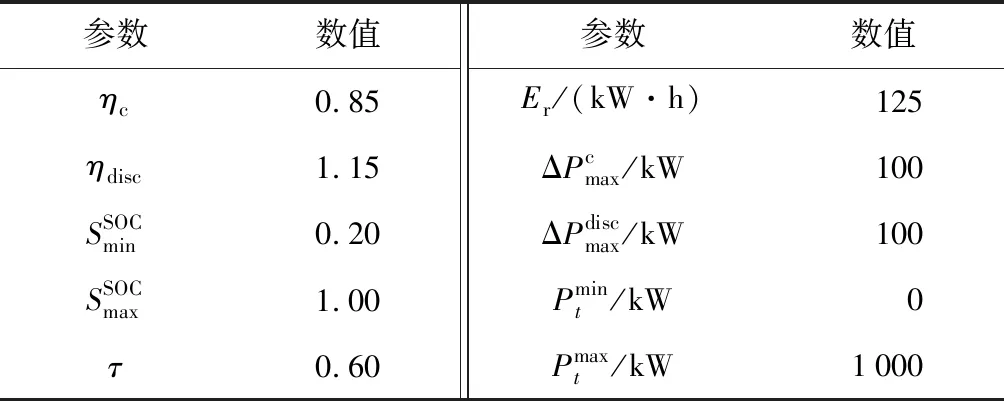
4.2 基于Wasserstein距离的全局灵敏度分析

以配电网中可再生能源机组的随机出力作为输入变量，以节点108处的PVUF(PVUF)作为输出变量，利用所提基于Wasserstein距离的GSA方法计算各个可再生能源机组出力的全局灵敏度指标.为提高全局灵敏度指标的计算效率，所引入BPNN模型的输入变量维度为5(3个风机与2个光伏电池的出力)，输出变量维度为1，设置1层隐含层(神经元数目为3).BPNN模型的训练样本集由 1 200 组输入-输出样本组成，经过27次迭代训练，最终所得模型的均方误差为6.25×10，满足所需精度需求.全局灵敏度指标计算时，每个随机输入变量的取值区间等分段数=20，采用MCS计算PVUF的采样次数为 100 000.考虑4个不同的共享ESD配置时段(时段1～4)，当=1，2时，可再生能源机组出力的-Wasserstein距离全局灵敏度指标计算结果分别如表4、5所示.

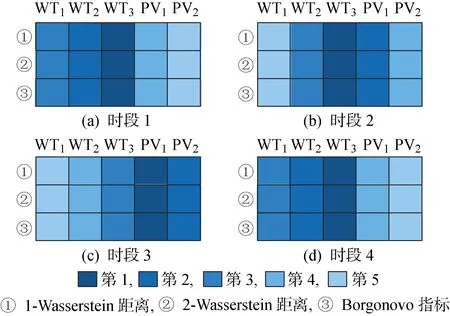
为验证所提全局灵敏度指标的有效性，计算了可再生能源机组出力的Borgonovo全局灵敏度指标，图6所示为3种方法分别计算得到的5个可再生能源机组出力全局灵敏度指标排序结果，对比可知，3种全局灵敏度指标所确定的机组重要性排序结果完全一致.方法①、②、③计算全局灵敏度指标的计算耗时分别为3.97、3.88 及15.87 s，说明本文所提方法在计算速度上优于Borgonovo指标法，这是因为本文所提方法与Borgonovo指标法的计算分别基于输出样本的CDF与PDF，而CDF的计算相较于PDF更加简单.因此，对比结果验证了本文所提方法的有效性.

进一步，由表4、5的计算结果可知，分别取1和2时基于-Wasserstein距离的全局灵敏度指标计算结果完全一致，且值的选择不会影响关键可再生能源机组的辨识.全局灵敏度指标的大小表征了可再生能源机组出力波动对配电网电压不平衡度的影响程度.由表4、5可知，在不同的共享ESD配置时段，辨识得到的对节点108处VUF影响程度最大的2个可再生能源机组会有所不同.其中，时段1与时段4中风机2和3的影响较为显著，时段2中风机3与光伏电池1的影响较为显著，时段3中光伏电池1和2的影响较为显著.上述所辨识的关键可再生能源发电机组将为共享ESD配置点的选择提供参考.

4.3 多时段共享ESD配置与优化运行

根据表4、5的全局灵敏度指标计算结果，多时段共享ESD的配置方案如表6所示.考虑共享ESD的位置与连接关系，具体配置如下：① 对于共享ESD，在时段1、4配置在WT处，在时段2、3配置在PV处；② 对于共享ESD，在时段1、2、4配置在WT处，在时段3配置在PV处.

共享ESD配置完成后，基于本文所提出的滚动预测优化方法优化ESD的运行方式，以降低节点108处的电压不平衡越限风险.假定可再生能源出力的预测误差随时间推移而不断增大，通过MCS生成100个随机场景，用以验证不确定性环境下所提共享ESD优化运行方法的有效性.

首先，随机选一个运行场景，所配置的2个共享ESD充/放电功率及相应的可再生能源机组出力情况如图7所示，图中为功率，ESD功率为正时表示处于放电状态，功率为负时表示处于充电状态.由图7可知，通过优化共享ESD的运行方式，在共享ESD配置的时段可再生能源机组的出力波动均得到了有效平抑.如图7(a)中，WT在时段1(1～6 h)的出力有较大的波动，呈现出剧烈的上升与下降趋势，在该时段内其峰谷差最大值为132.9 kW.在配置ESD后，利用滚动预测优化方法，单个时段内风机WT-共享储能ESD的联合出力较为平缓，峰谷差最大值为34.2 kW，相比未配置ESD前降低了74.3%.图7共享ESD投入运行的全部时段中，单个时段可再生能源机组出力峰谷差最大值为 407.9 kW，而可再生能源与共享ESD联合出力的峰谷差最大值为296.6 kW，相比配置ESD前输出功率的峰谷差降低了27.3%.上述仿真结果表明共享ESD的配置与滚动优化运行显著降低了可再生能源发电波动性，从而为降低可再生能源随机出力导致的配电网电压不平衡越限风险提供了可能.

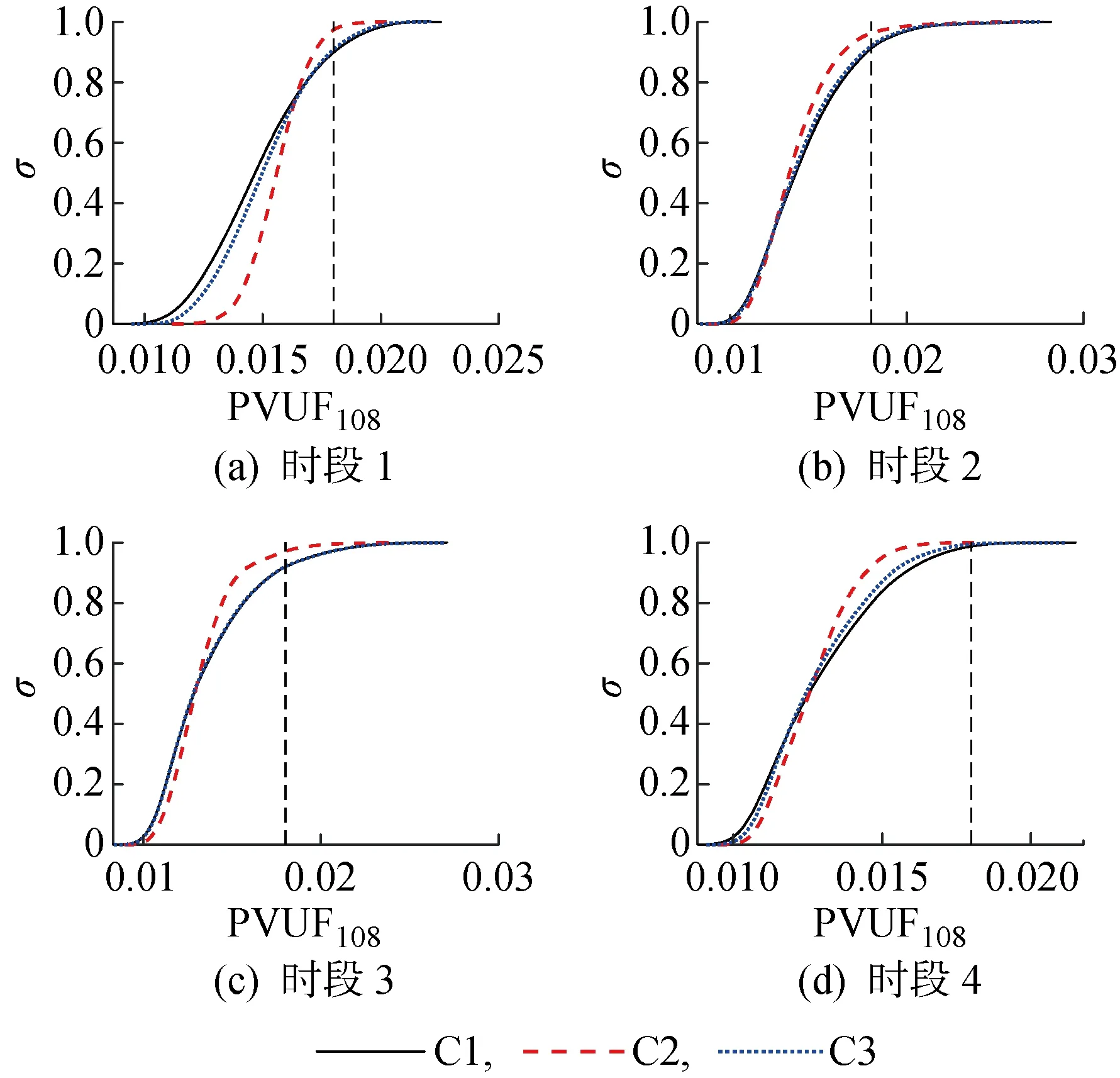
为了验证多时段共享ESD配置策略的有效性，本文对比了以下3种共享ESD配置策略降低配电网概率电压不平衡度越限风险的效果：C1为共享ESD不接入配电网；C2为将共享ESD配置在GSA方法辨识得到的关键可再生能源机组处滚动优化运行；C3为将共享ESD配置在非关键可再生能源机组处滚动优化运行.需要说明的是，光伏电池在时段1、4(夜间)没有出力，因此所设置场景在这两个时段下不会将共享ESD配置于光伏电池处.在本算例中，设置配电网节点PVUF的容许阈值=0.018.对于上述3种情况，分别求取100个随机运行场景下PVUF分布曲线，如图8、9所示.图中为概率密度，为累积概率.

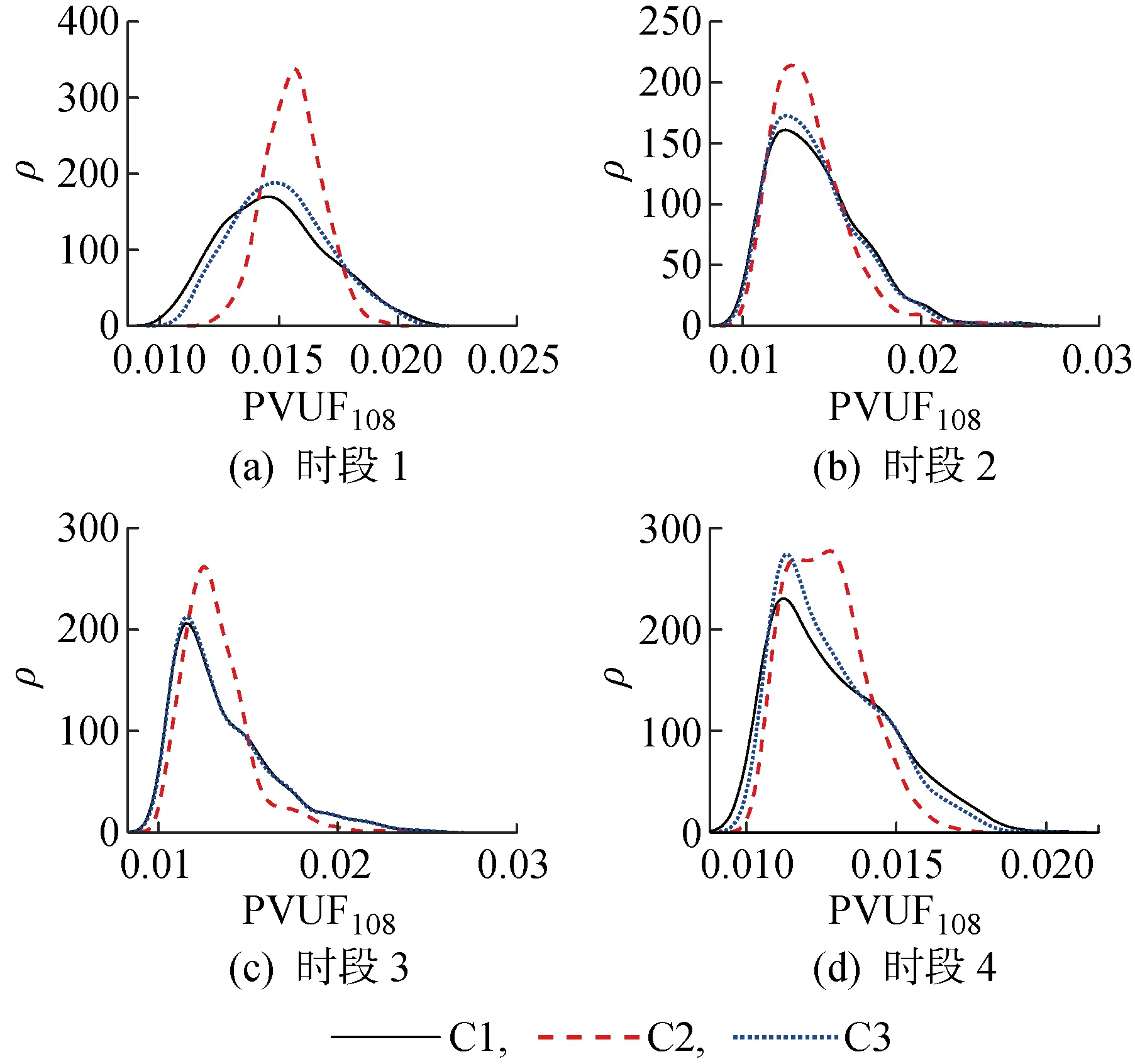
由图8可知，相比于不接入共享ESD(C1)，在GSA方法所辨识的关键可再生能源机组处配置共享ESD(C2)，将会使得PVUF概率分布更加集中，波动性降低，从而降低越限风险.然而，在非关键可再生能源机组处配置共享ESD(C3)，PVUF的概率分布几乎与C1的结果相同，表明共享ESD的接入并未发挥显著作用.

一、出去直接把仓库门锁上，再去叫人，这样大家都知道小偷是丁主任而不是我，那么，哈哈——我的嫌疑洗清了，但是……但是……丁主任的前途也就毁了，说不定还成了阶下囚。如若这样，我是不是太狠毒了，我可是长辈，不能不顾及孩子的将来，而且这孩子平时待自己也不薄啊，他前几天都不是说了吗，如不是小偷，让我回去看看老婆孩子。

由图9可知，在PVUF的容许阈值处(图中黑色虚线)，C2中的PVUF累积概率相比C1与C3有所提高，即C2中PVUF在容许阈值以下的概率提高，说明应用所提共享ESD配置策略与优化运行方法能够使PVUF的越限概率下降.由图9的累积概率函数可进一步计算PVUF的越限风险指标.对应4个时段，在关键可再生能源机组处配置共享ESD(C2)后，PVUF的越限风险指标从不接入共享ESD(C1)时的9.9%、8.4%、8.0%及1.2%降低至2.3%、3.7%、2.9%及0.0%，而在非关键可再生能源机组处配置共享ESD(C3)后基本保持不变.算例结果表明，本文所提出的GSA方法通过辨识关键的可再生能源机组出力，能够为共享ESD的配置提供有效引导作用.并且，应用所提共享ESD配置策略与优化运行方法，能够有效降低不确定性环境下配电网的概率电压不平衡越限风险.

③在开始学习阅读或识字的阶段，阅读很容易走神，可能需要手指帮忙才能顺利地开始阅读，并且在开始阅读很长时间以后还是不能摆脱这种习惯。

为了验证本文所提滚动预测优化运行方法能够有效减小可再生能源预测误差的影响，进一步对比现有文献中不考虑预测误差影响的方法，设置对比场景(C4)：在关键可再生能源机组处配置共享ESD后，仅在每个运行时段开始前更新可再生能源预测出力，并制定共享ESD的运行方式，在运行时段内不再进行滚动预测优化.求取该情况下100个运行场景PVUF的分布曲线，并与C2对比如图10所示.由图10可知，基于滚动预测优化方法的共享ESD参与运行后(C2)所得PVUF的概率分布相比于C4中的结果更加集中，方差变小，因此共享ESD的运行效果更加显著，能够更有效地降低可再生能源随机出力影响下节点108的电压不平衡越限风险，验证了所提滚动预测优化运行方法的有效性.

在继电保护技术应用在智能电网的建设当中时，必须要对多个问题来进行考虑，从根本上实现继电保护技术在智能电网建设中的应用。

5 结论

本文以配电网三相电压不平衡越限风险为研究对象，建立基于BPNN的PVUF计算代理模型，定义了PVUF越限风险指标，引入基于Wasserstein距离的GSA方法，提出了基于全局灵敏度指标的多时段共享ESD配置策略及其滚动预测优化运行方法，有效降低了配电网的电压不平衡越限风险.主要结论如下.

(1) 基于Wasserstein距离的GSA方法通过计算可再生能源机组出力的全局灵敏度指标，能够准确量化可再生能源机组随机出力对配电网电压不平衡度的影响程度，并为共享ESD的配置提供指导.

(2) 基于全局灵敏度指标的共享ESD配置策略与基于滚动预测优化的ESD运行方法能够利用数量有限的ESD，平抑关键可再生能源机组的出力波动，有效减小不确定性环境下配电网概率电压不平衡度的波动范围，从而降低配电网概率电压不平衡度越限风险.

下一步工作将研究考虑多输出变量的GSA方法及其在配电网运行中的应用，结合相应的ESD配置与优化策略，保障配电网安全运行.