线性插值公式在微积分求解中的应用

薛 洁，余 芬

(亳州职业技术学院 基础教学部, 安徽 亳州 236800)

微积分是近代数学的重要分支，内容主要包括函数、极限、微分学、积分学及其应用。目前微积分知识已经应用到财务管理、信息传输、建筑工程以及机械设计等领域中。微积分问题的研究一直与物理问题紧密相关，且有很多科研成果是使用微积分计算得出的。在微积分的研究历史中，阿贝尔最早提出规范化解题思想，后经过众多学者前仆后继长达数百年的研究，高等数学中的微积分与函数理论、解析几何、数学概论等学科融合在一起，但微积分一直在高等数学中占有不可替代的位置[1]。随着数学解题思想的形成，微积分的解题方法与思维开始呈现多元化的建设趋势。由于在插值节点上的插值计算结果误差为零，因此本文应用线性插值公式，即一次多项式的插值函数的方式，进一步提高微积分求解精度。线性插值区别于其他插值，此种插值方式计算过程简单、计算结果准确。在指定的情况下，线性插值公式可以代替原函数计算公式，也可用于计算插值表格中没有的数值[2]。因此，本文将基于线性插值公式，展开微积分求解方法的设计。使其计算结果的精度更高。

1 线性插值公式的适用性

由于线性插值公式在一定约束条件下，可以有效地代替原函数，因而线性插值公式可用在差分函数的计算过程中，根据数值算法，对计算结果进行数值误差分析，并结合算例分析，对计算数值进行稳定性估计。

截至目前，线性插值公式已被广泛应用到积分算子计算与微积分方程的计算过程中，切合实际地解决了包括物理工程、生物经济等领域的较多科研问题[3]。

2 基于线性插值公式的微积分求解方法

2.1 设定微积分方程

在利用线性插值公式求解微积分问题的过程中，必须预先设定微积分方程[4]。本文结合高等数学中的微积分理论设定微积分方程，选取一条曲线，设在曲线中存在节点M(x,y)，由M(x,y)的切线斜率C可得此条曲线的表达式，于是有如下公式：

(1)

式中，Q为节点横纵坐标连接直线距离，y为节点的纵坐标，x为节点的横坐标。通过公式(1)，得出此条曲线方程。根据基尔霍夫定律，将公式(1)写为两端积分的形式，可得如下公式：

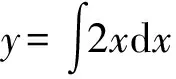
(2)

通过公式(2)得出微积分方程。在此基础上，本文为实现基于线性插值公式的微积分求解，还需要进行2点基本假设[5]：第一点为假设高等数学中微积分方程目标函数存在连续单调不减性质；第二点为基于线性插值公式的微积分求解结果为存在性结果，即为已知存在方程解[6]。在满足以上两点基本假设的前提下，将线性插值公式应用在微积分中，为下文基于线性插值公式线性逼近微积分函数提供基础参数。

2.2 基于线性插值公式线性逼近微积分近似值

在设定微积分方程的基础上，本文利用线性插值公式，将曲线划分为若干个区间，通过线性插值公式近似区间中的积分函数，逼近高等数学微积分函数[7]。设已知存在的方程节点M(x,y)在[0，T]，则基于线性插值公式作曲线等距划分如下：

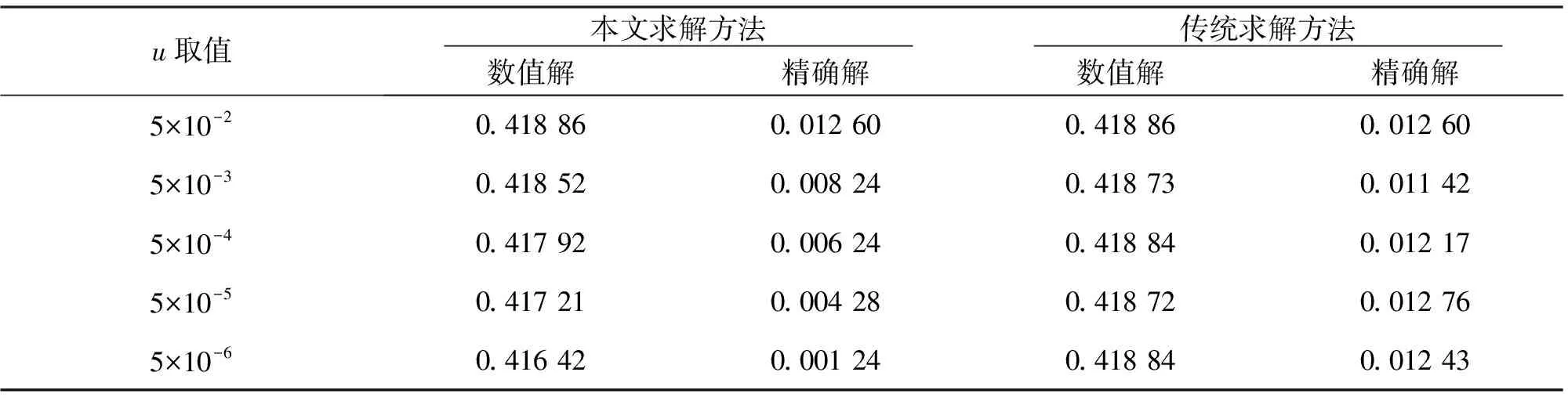
△：0=t0

(3)

式中：n为线性插值公式近似区间个数，为实数；tn为等距划分线性插值公式近似区间(个数为n)的分割点。利用公式(3)，基于线性插值公式作曲线等距剖分，计算微积分节点M(x,y)存在方程解的近似值。设M(x,y)方程解近似值的计算表达式为u，具体计算公式如下：

(4)

式中，s为当前线性插值公式近似区间的数值积分，tn+1指的是当前等距划分线性插值公式近似区间(个数为n+1)的分割点。利用公式(4)，基于线性插值公式线性不断逼近微积分近似值，将微积分求解问题转化为可分离变量[8]求解问题。在基于线性插值公式线性逼近微积分近似值的过程中，必须要考虑到隐式通解的问题。此时，需要由欧拉公式将微积分近似值u设置为任意复数或是任意回复数，基于此，可得如下方程：

u=e(-kx+C)=C1e(-kx),

(5)

式中，e为微积分函数的定义域，k为微积分函数隐式通解中存在的可分离变量，C1为曲线中节点M(x,y)切线斜率的任意常数。在得出公式(5)的情况下，基于线性插值公式进行Taylor展开，则有如下公式：

u=s(tn,x(tn))+s′(ξi,x(ξi))(s-tn)。

(6)

式中：i为线性插值公式线性基本特性估计参数，为实数；ξi为线性插值公式线性基本特性系数。通过公式(6)，可基于线性插值公式线性逼近微积分近似值，并解决微积分求解中的隐式通解问题。

2.3 校正微积分求解误差

在基于线性插值公式线性逼近微积分近似值后，考虑到由于基于线性插值公式线性逼近过程中会导致微积分求解误差[9]。所以必须校正微积分求解误差，以确保高等数学微积分求解精度。本文运用线性插值公式中的双边极值定理，提高微积分目标函数方程求解的收敛速度，实时校正微积分求解误差[10]。设基于线性插值公式双边极值定理求解公式F，可得计算公式(7)为

(7)

表1 基于线性插值的数值算法误差校正综合信息

由表1可知，基于线性插值的数值算法误差校正能够使M(x,y)节点向微积分近似值误差小的方向逼近，进而起到校正微积分求解误差的效果。

2.4 输出微积分求解积分曲线

在线性插值公式中，设定微积分求解误差能够通过倒向积分求得最优校正结果，且不存在解析解。通过此种方式，将线性插值公式中的倒向积分用自适应权重进行表示，也就是说每一种微积分求解方法都会有与其对应的自适应权重[12]。通过计算的方式，可达到微积分求解的目的。设微积分自适应权重为ε，则有如下公式：

(8)

通过此方程式，当倒向积分接近微积分最优解时，自适应权重的值减小；当倒向积分远离微积分最优解时，自适应权重的值增大，以此可实现微积分求解，进而达到提高微积分求解收敛速度的目的[13]。

在此基础上，首先设置微积分求解积分曲线的基础坐标点为(x0,y0)以及(x1,y1)；而后，基于线性插值公式的线性特征，连接4个点位，通过插值系数的基本点，得到微积分求解积分曲线，输出高等数学微积分最优解[14]。设微积分最优解的表达式为f(x)，如公式(9)所示：

(9)

通过公式(9)，可得到微积分方程式最优解。基于线性插值公式的线性特征，输出微积分求解积分曲线[15]，如图1所示。

在图1中，A、B为插值系数，f(x)为微积分最优解，根据微积分求解积分曲线，实现基于线性插值公式的微积分求解。至此，完成线性插值公式在微积分中的应用。

3 对比实验

3.1 实验准备

本文通过上述论述设计了一种全新的基于线性插值公式的微积分求解方法，为验证该方法在实际应用中是否具有更优的求解效果，将该求解方法与传统求解方法进行对比实验，验证两种算法的求解误差。将两种求解算法引入到实际算例当中，为保证实验最终结果的公正性及有效性，在进行求解的过程中，均采用本文中提到的M(x,y)方程解近似值。

3.1.1 实验假设

在考虑Capuio分数阶导数的情况下，假设其初始值u的取值为u=0，根据本文描述把M(x,y)方程解近似值的计算表达式u作为自变量。表2为M(x,y)方程解近似值的计算表达式u的变化范围。

表2 M(x,y) 方程解近似值的计算表达式的变化范围

此次实验共分为5组。设置相应初始值的u的范围，为保证实验科学性，其中第一组取值为5×10-2，第一组取值是第二组的10倍，第二组取值是第三组的10倍，以此类推，直到5组取值完成。

3.1.2 实验过程

为保证实验及实验结果具有普遍性，且u在其相应的范围内，选择其中间值作为实验对象，即自变量参数。首先，利用本文上述求解方法根据u的取值变化进行多次计算；再利用传统求解方法根据u的取值变化进行多次计算；组后，将2种计算结果进行记录，对比相应的计算结果。

3.2 实验结果分析

为保证实验结果能够更加明显地将2种算法的实际应用效果体现，选择2种求解算法的数值解以及精确解作为对比参数，如果数值解和精确解能够随着u的变小而出现明显的线性变化，则证明算法的求解精度更高。2种求解方法的计算结果见表3。

表3 2种求解方法数值解及精确解对比

根据表3中的数据，当u的取值为0.05时，本文求解方法与传统求解方法的数值解与精确解均相同。因此，说明在u=5×10-2时，2种方法均能够得到相同的精确数值。当u的取值为5×10-3时，2种求解方法的数值解和精确解开始出现明显的变化。随着u取值的不断变小，本文求解方法中的数值解和精确解均逐渐减小，而传统求解方法的数值解和精确解呈现出不规律的变化，时而增加时而减小。

综上所述，本文提出的基于线性插值公式的微积分求解方法求解结果的精度更高，可达到小数点后6位。在实际应用中，利用本文提出的求解算法能够保证结果的准确性，并且具有一定的收敛性，能够适用于某一领域中对不同问题的系统性分析与计算。

4 结语

本文通过分析线性插值公式的适用性，提出一种基于线性插值公式的高等数学微积分求解方法，并通过设计对比实验的方式，验证了本文提出的基于线性插值公式的微积分求解方法与传统求解方法相比，求解结果的精度更高，可达到小数点后6位。在实际应用中，利用本文提出的求解算法能够保证结果的准确性，并且具有一定的收敛性，适用于某一领域中对不同问题的系统性分析与计算。