一类新的广义Fibonacci数列的通项和性质
曾文建
(福建信息职业技术学院 基础教学部,福建 福州 350007)
Fibonacci数列是一个古老而颇有特色的递推关系数列,它有很多奇妙而有趣的性质[1-2],深受广大数学爱好者和科研工作者喜欢。Fibonacci数列和广义的Fibonacci数列已深入到数学的各个领域,并在物理学、控制论、运筹学、金融学、生物学等领域中起着非常重要的作用。广义Fibonacci数列有着许多的形式,如文献[3]给出了几种形式,有的学者给出它的一些很好的性质[4-6],有的学者给出其求和公式[7-9],有的学者给出关于它的一些恒等式[10-11]。本文将进一步研究一类新的广义Fibonacci数列,利用矩阵和递推关系,推出其通项公式,得到了一些新的性质和求和公式。
1 预备知识
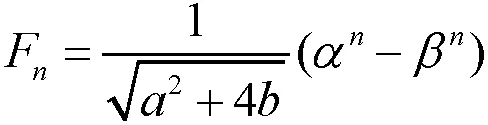
现对广义Fibonacci数列1进行推广。
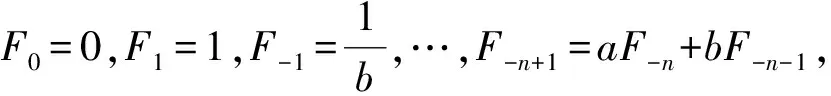
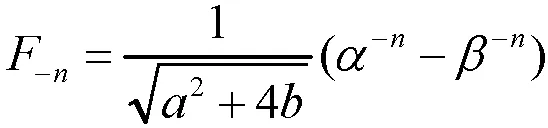
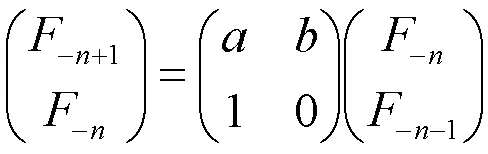
证明用矩阵表示,
所以有
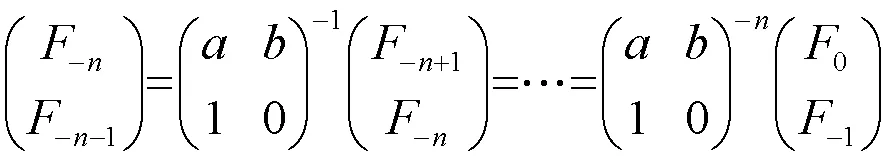

记,特征方程f(λ)=
特征值为α-1,β-1,由哈密顿-凯莱定理,有
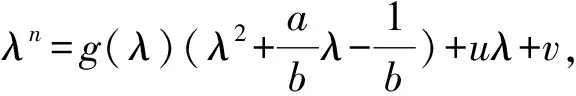
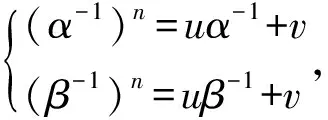
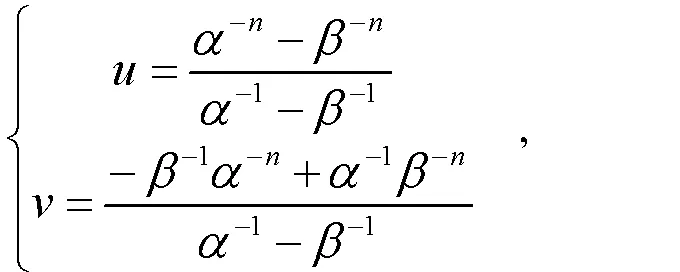
解得
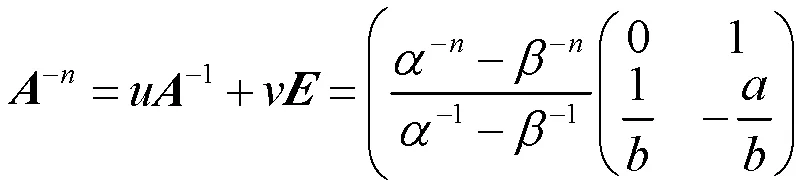
所以
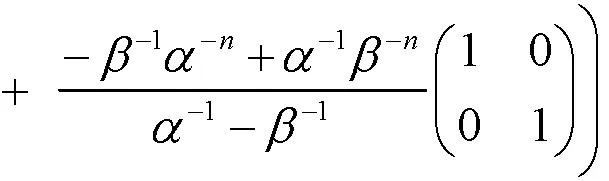

计算矩阵第2行第2列:
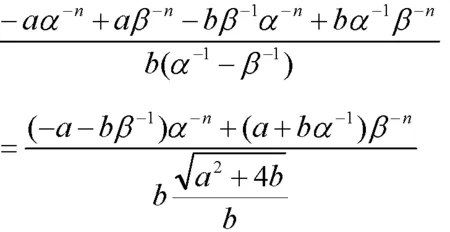
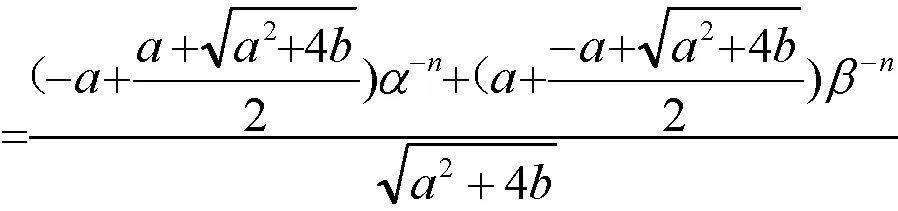
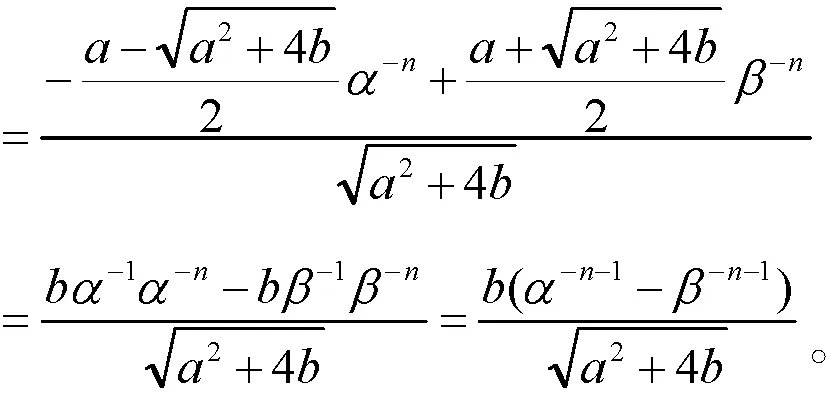
2 性质证明
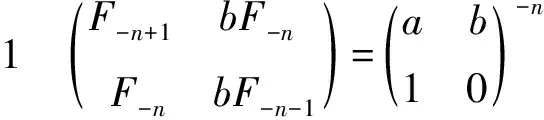
证明当n=1时,
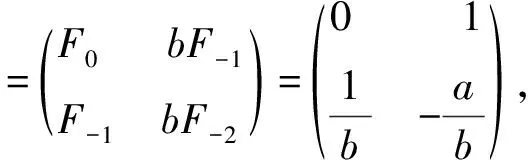
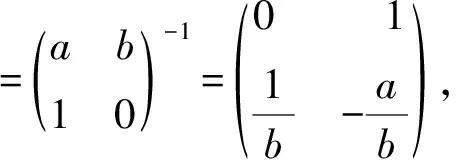
假设当n=k时, 等式成立,那么
即当n=k+1时,等式也成立,性质1得证。
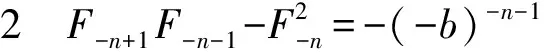
证明对性质1两边取行列式, 化简,由性质2得证。

证明左边
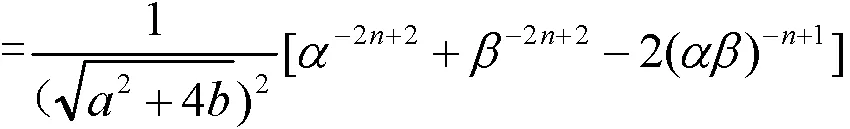
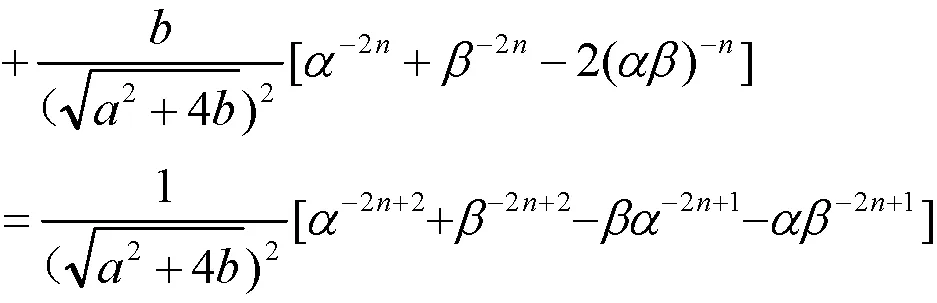
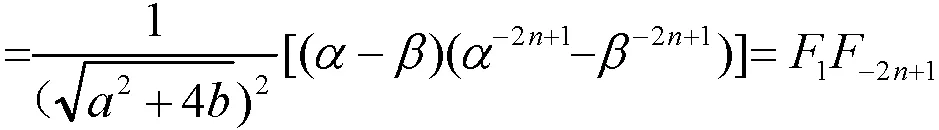
性质3得证。
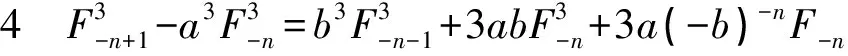
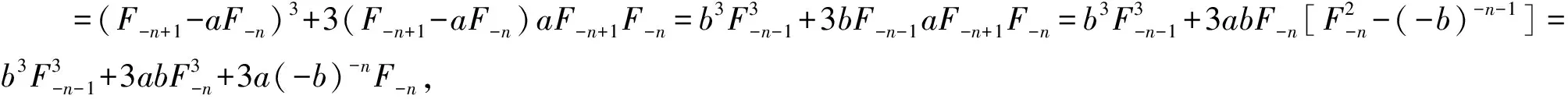
性质5F-m-n=bF-mF-n-1+F-m+1F-n
证明右边
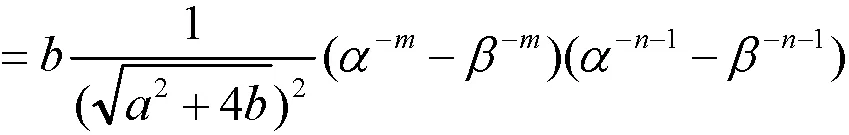
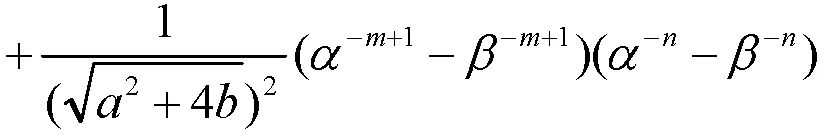


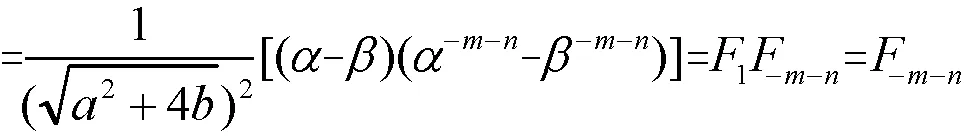
性质5得证。
3 求和公式
公式1F-1+F-2+…+F-n=
证明设X=F-1+F-2+…+F-n,
则aX=aF-1+aF-2+…+aF-n,bX=bF-1+bF-2+…+bF-n,
进而有aX+bX=bF-1+F0+F-1+F-2+…+F-n+1-bF-n-1,
(a+b-1)X=1-F-n-bF-n-1。
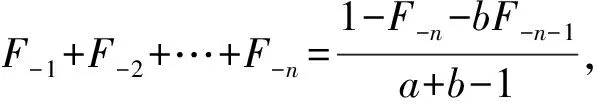
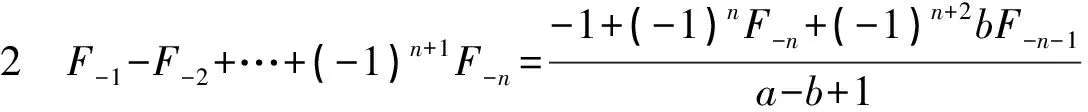
证明令Y=F-1-F-2+…+(-1)n+1F-n,
则aY=aF-1-aF-2+…+(-1)n+1aF-n,
bY=bF-1-bF-2+…+(-1)n+1bF-n,
aY-bY=-bF-1+F0-F-1+…+(-1)n-1F-n+1+(-1)n+2bF-n-1,
(a-b+1)Y=-1+(-1)nF-n+(-1)n+2bF-n-1,

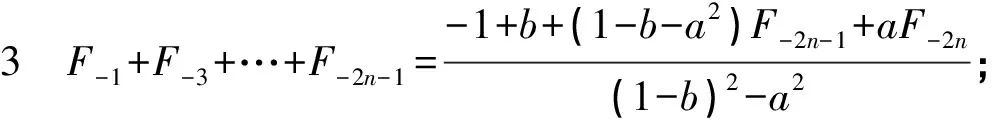
证明令u=F-1+F-3+…+F-2n-1,v=F-2+F-4+…+F-2n,那么
(1-b)u=-bF-1-(bF-3-F-1)-…-(bF-2n-1-F-2n+1)+F-2n-1
=-1+aF-2+…+aF-2n+F-2n-1=-1+av+F-2n-1,
(1-b)v=F-2+F-4+…+F-2n-bF-2-bF-4-…-bF-2n
=-bF-2-(bF-4-F-2)-…-(bF-2n-F-2n+2)+F-2n
=-bF-2+aF-3+…+aF-2n+1+F-2n
于是得到方程组
当(1-b)2-a2≠0时,利用行列式性质可得
公式得证。
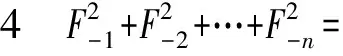
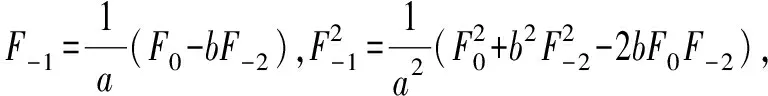

由性质2,并利用等比数列求和公式,代入上式化简得
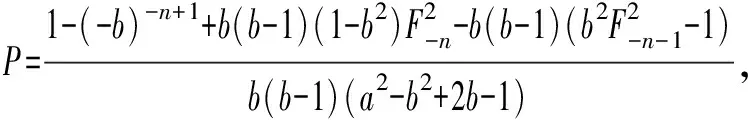
随着指数越来越大,对广义Fibonacci数列2的求和计算就变得越来越复杂。本文对广义Fibonacci数列2的研究,丰富了广义Fibonacci数列1的内容和内涵,拓展了人们对广义Fibonacci数列1的视野,提出了更多的研究课题,很好地推动了广义Fibonacci数列的研究和发展。

