一类分数阶模拟小波滤波器的电路实现
邹子贤, 李宏民, 李春来, 钱 坤
(湖南理工学院 物理与电子科学学院, 湖南 岳阳 414006)
0 引言
模拟小波滤波器是分析非平稳瞬态信号的强大工具[1], 已广泛应用于信号分析、图像处理、故障检测、生物医学工程等领域[2].然而, 随着研究对象和范围的不断扩大, 模拟小波滤波器在处理一些问题时的局限性逐渐暴露出来.例如, 为满足低压、低功耗、高精度的市场需求, 模拟小波滤波器的阶数在不断提升,这意味着研发成本也将不断增加.同时, 许多新兴应用所需的规范使非整数阶模拟滤波器成为更好的选择.为了便于该类滤波器的实现, 现有技术方法是将所需的阶次四舍五入到最接近的整数.正是由于阶次的近似, 无法精确实现模拟小波滤波器的幅频响应与相频响应.另外, 刻度有限的整数阶模拟小波滤波器很难满足更详细的非平稳特性分析的需求.近年来, 滤波领域中应用分数阶微积分理论所带来的额外自由度或许能为上述问题提供应对策略.根据Riemann-Liouville公式, 分数阶微分可被定义为
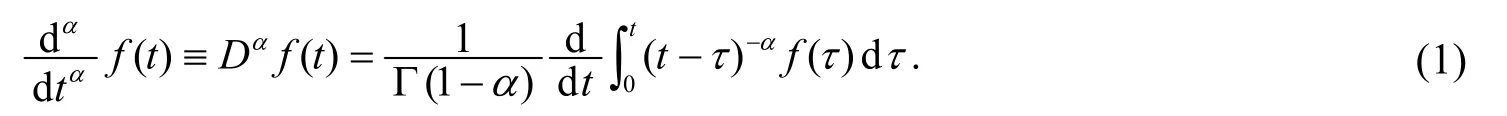
其中α为实数, Γ(·)为Gamma函数.在零初始条件下, 式(1)的拉普拉斯变换为

如图1所示, 可以定义一种阻抗与sα成比例的通用分抗元件[3], 其中常规元件如电阻、电感、电容以及频率相关负电阻被认为是分别对应于α= 0,1,- 1, - 2的特殊情况.在滤波器中使用分抗元件可以将电路从整数域扩展到更一般的分数域.例如, 传统的模拟小波滤波器可以被归类为一阶、二阶或n阶电路, 其中n为整数.为提高模拟小波滤波器的逼近性能, 往往要将n阶滤波器提升至(n+1)阶.而当α∈ (0,1)时, (n+a)阶分数阶模拟小波滤波器填补了n~(n+ 1)阶之间的空白.这不仅降低了电路的研发成本, 还能精确实现滤波器的频率响应.另外, 分抗元件所提供的自由度提高了设计灵活性.例如, 传统整数阶滤波器的阻带衰减速率被限制为20ndB/dec, 然而分数阶滤波器的阻带衰减速率能以20(n+α) dB/dec 被精准控制.

图1 分数阶元素分类
在文[4]的基础上, 本文首先利用Foster Ⅰ型RC串并联网络近似分数阶电容, 然后采用改进型KHN滤波器结构搭建Marr小波基的6.4阶同元次电路.最后, 将分数阶滤波器的数值仿真和电路仿真结果进行详细比较, 验证所提出的电路设计方案的可行性.
1 分数阶模拟小波滤波器设计
1.1 分数阶模拟小波滤波器传递函数设计
高斯族小波基体现为高斯函数的微分形式, 由高斯函数的时频表达式, 有

其中τ为高斯函数的尺度因子.结合式(3)与傅里叶变换的高阶微分性质F[f(n)(t) ]=(jω)nF(ω),可以推出频域中高斯族小波的通式为

为完成式(4)的有理分式逼近, 还需重述连续小波变换的定义式(设输入信号f(t) ∈L2(R)且为平方可积函数):
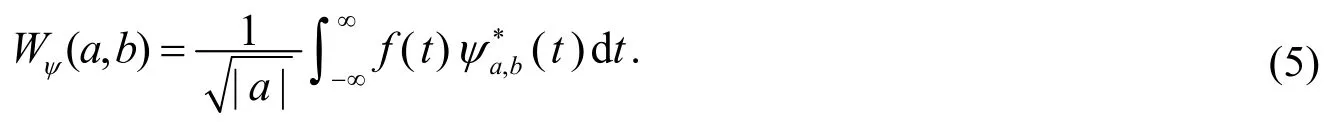
其中

ψ(t)称为小波基,a和b分别为尺度因子与平移因子.根据滤波器理论, 式(5)可以用卷积改写为

可见, 尺度因子为a的连续小波变换可看作输入信号f(t)通过一个冲激响应为的滤波器后的输出y(t).所以, 只需设计一组冲激响应分别为高斯族小波反褶函数的滤波器(高斯族小波滤波器)就能实现高斯族小波的多尺度小波变换.首先, 在构建高斯族小波基的数学近似模型时引入非整数阶次α,从而完成对高斯族小波的分数阶逼近.然后在后期优化算法中引入约束项, 以确保所设计的小波滤波器满足因果性、稳定性、小波容许准则等约束条件.最后, 利用2L范数误差通过离散化的数值计算量化分数阶小波基与理想高斯族小波基之间的逼近误差,从而将高斯族小波基的有理逼近过程转换为高维度、多峰复杂的非线性寻优问题.另外,虽然分数阶次α所带来的额外自由度增加了设计灵活性,但自由参数的过度增加同样会降低小波逼近网络的精度和增大后期优化算法搜索的难度.为避免上述问题发生,我们采用同元次传递函数逼近高斯族小波基[5].根据同元次传递函数中阶次均为基阶β整数倍的特性,高斯族小波的分数阶数学近似模型可以被构建为其中n为阶数的整数部分,α为阶数的小数部分且(n+2β)/β,…,(1+β) /β∈N,基阶β需满足β/γ∈N,γ为正实数,B1,B2,…,Bn是待优化目标参数,向量x代表待优化目标参数Bi(i= 1,2, …,n),pi代表传递函数Ha,α(s)的极点,M为采样点个数,Δω为采样间隔.为完成高斯族小波滤波器传递函数的设计,还需选取一个具体的高斯族小波作为设计对象.这里以尺度a=1的Marr小波(高斯二阶导数)为例,将参数设置为待优化系数Bi(i=1,2,… ,n),在(0,6)的范围内被寻优,最高阶的整数部分n= 6,基阶β=0.2,初始种群大小N=1000,最大迭代次数iteration=4000,频率ω的范围为0~7rad/s,采样点个数M= 701,采样间隔Δω=0.01rad/s.然后利用基本粒子群算法[6]搜寻式(8)的全局最优位置,其优化结果见表1.
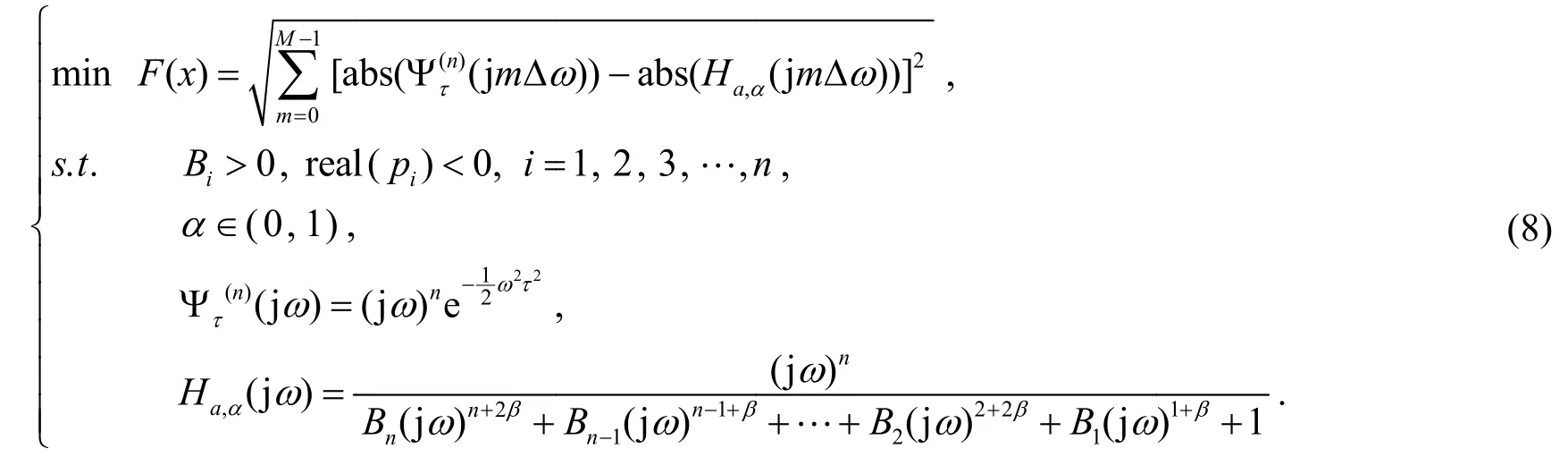

表1 6.4阶Marr小波基优化结果
将表1中所求得的优化值代入式(8)中,则6.4阶Marr小波基可以被表达为
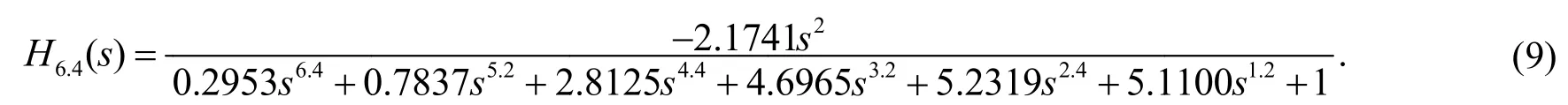
计算表明,6.4阶Marr小波基的L2范数误差仅为0.3258.图2说明了6.4阶Marr小波基在时频两域均对理想小波基有着良好的逼近效果.

图2 6.4阶Marr小波基冲激响应与频率响应
1.2 分数阶模拟小波滤波器电路设计
实验研究表明,6阶或7阶的整数阶滤波器就能对Marr小波进行较好的逼近.因此下文以6.4阶Marr小波基的同元次电路实现为例,验证所提电路方案的可行性,类似的过程也可应用于其他高斯族小波滤波器的实现.传递函数的一般形式可以被描述为

式(10)经过变形可得
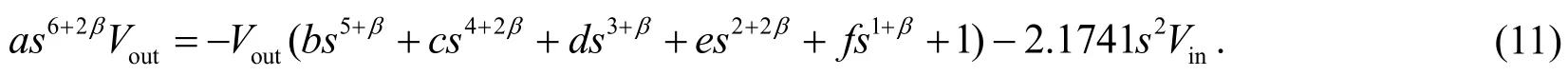

根据式(12)设计电路的信号流图如图3所示.

图3 6.4阶Marr小波滤波器信号流图
结合改进型KHN滤波器拓扑结构[7],根据该信号流图能得到如图4所示的电路,其中Ui(i=1,2,…,6)为α阶分数阶电容.
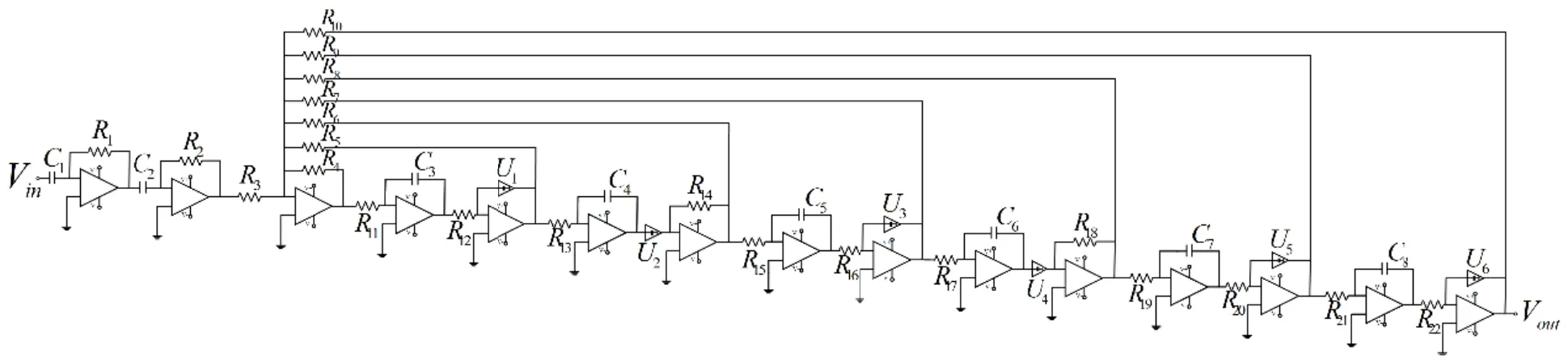
图4 6.4阶Marr小波滤波器电路
该电路有两大优势:(1)由于单个元器件的实际值与标称值的偏差在±7%左右,那么所累积的整体误差会给小波滤波器的实际应用带来一定的困难.本文所采用的电路结构的传递函数中的系数皆由元件阻抗值的比例而定,而非单个元件阻抗值,这在很大程度上能减少阻抗值偏差带来的影响.(2)虽然该电路中放大器数目较多,但只需改变个别电阻值就能实现不同参数要求的小波滤波器,这极大地提高了电路的灵活性.
将电路中所有的反向放大器的系数均设为1,则图4对应的传递函数为

值得注意的是,分数阶电路中的关键模块如微分器与积分器都需要分数阶电容的参与,但遗憾的是目前并没有商用推广的分数阶电容存在,因此本文利用Foster Ⅰ型RC串并联网络近似分数阶电容.相较于其他近似网络,Foster Ⅰ型网络实现难度低且幅频响应误差小,并能在一定频率范围内很好地模拟分数阶电容,其等效阻抗

其中ri为留数,pi为极点,k为直项.上述数据值会与图5所示的Foster Ⅰ型电路中元器件值相对应,其关系为R0=K,.
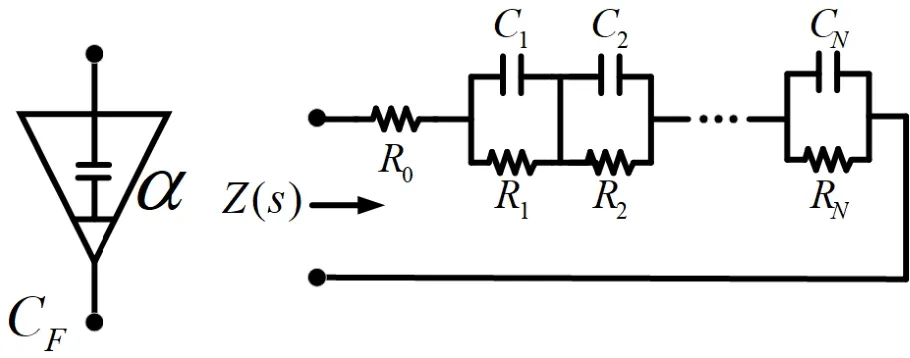
图5 Foster Ⅰ型RC串并联网络近似原理
2 电路仿真
本文采用的α阶电容是根据Oustaloup算法设计出的模拟分数阶电容[8],通过设定α阶电容的阶数和工作频率范围,从而确定FosterⅠ型网络中各电阻电容值.具体来说,令α=0.2,Ui(i=1,2,… ,6)=1F,频率ω的范围为 10-4~102Hz,零极点对数N= 7,则电容值为1F的0.2阶模拟分数阶电容如图6所示.

图6 0.2阶模拟分数阶电容
利用PSPICE软件将图6所示的模拟分数阶电容电路分别封装成图4中的Ui(i= 1,2,… ,6),那么在10-4~102Hz频率范围内Ui(i=1,2,…,6)能被视为分数阶电容.通过计算,6.4阶Marr小波滤波器中各电阻电容取值见表2.
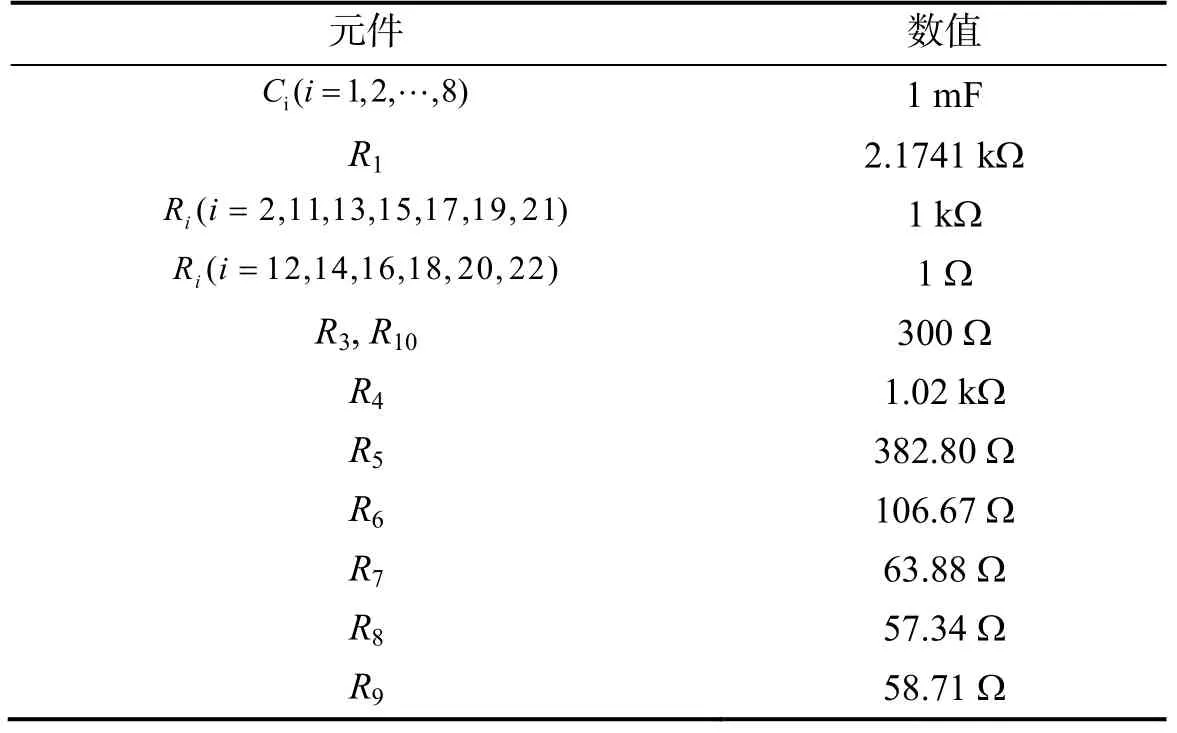
表2 6.4阶Marr小波滤波器元件取值
通过对上述电路进行仿真,能得到图7所示的电路仿真结果.然后将该结果与前文的数值仿真结果进行对比,不难发现,6.4阶Marr小波滤波器的频率响应与理论值基本吻合,且实际阻带衰减速率为129.5dBdec,与理论值128dBdec相差并不大.二者之间依然存在一定的误差,其主要原因为模拟分数阶电容的近似误差和Oustaloup算法在泰勒级数展开时所产生的截断误差.

图7 6.4阶Marr小波滤波器电路仿真结果与数值仿真结果
3 结论
本文通过计算高斯族小波滤波器传递函数通式中的系数,设计了一种可行的电路方案来实现分数阶模拟小波滤波器.以6.4阶Marr小波滤波器为例,验证了该方案的有效性.仿真结果表明,该方法不仅能继承分数阶电路的众多优点,还可以对整个高斯族小波进行良好逼近,从而实现以更小的步长精准控制小波滤波器的阻带衰减速率.虽然模拟分数阶电容所带来的近似误差会随着滤波器阶数的增加而不断累加,但如果未来出现了商用推广的分数阶电容, 则该误差可以被消除.

