基于奇异值分解的改进GRAPPA算法研究

魏小琴, 何汶静, 李 杨， 杜 勇

(川北医学院附属医院 a.医学影像学院； b.影像科，四川 南充 637000)

0 引 言

磁共振成像(Magnetic Resonance Imaging,MRI)是利用磁共振原理，对物体内部结构进行成像，MRI由于其超高的软组织对比度，在医疗诊断中有着举足轻重的作用。磁共振成像中使用多通道相控阵线圈接收磁共振扫描信号，每个线圈含有整个成像空间中的所有信号，这种多通道采集的信号冗余使得加速成像成为可能。并行磁共振成像(parallel Magnetic Resonance Imaging, pMRI)技术正是利用这种信号冗余可压缩的特性以及频率空间(也被称为K空间(k-Space))的相关性，通过减少信号的采集量(即减少相位编码次数)来实现节约扫描时间提升扫描速度。影响pMRI成像的主要两个因素是：K空间信号数据采样扫描时间与由K空间信号数据进行重建的图像质量[1]。pMRI在医疗图像高速成像及图像重建领域已有长足发展，该技术已应用于各大磁共振设备。

pMRI图像重建技术目前主要分为两类：一类为基于图像域的重建，该类算法主要利用线圈灵敏度进行图像重构，得到无伪影图像，代表算法有敏感度编码(Sensitivity Encoding，SENSE)及随后发展出的扩展方法SC-SENSE(Self-calibrating)、PILS(Parallel Imaging Local Sensitivities)等，该类算法要求通道线圈有更为精确的灵敏度，线圈灵敏信息由采集低频信号计算而得，当灵敏度已知，文献[2-3]中将压缩感知与SENSE 结合，增加正则项，取得了较好的重构效果，而准确估计往往非常困难。另一类是基于K空间数据重建技术，该类技术采集中间低频信号行数据作为自校准信号( Auto Calibration Signals,ACS)，用于计算出多通道线圈的权重系数，用这些权重系数拟合欠采样缺失数据，再将其重建为诊断图像。这种多通道直接重构最终图像，不需要估计线圈灵敏度，代表算法有AUTO-SMASH(Simulataneous Acquisition of Spatial Harmonics)、GRAPPA(Generalized Auto-calibrating Partially Parallel Acquisitions)和VD-AUTO-SMASH(Variable Density-AUTO-SMASH)算法[4]等。

目前GRAPPA算法对2倍降采样能够很好重建出没有卷褶伪影的图像，但对于3倍以及3倍以上的高倍数降采样的重建，由于拟合精度不够导致重建结果SNR降低或是仍然还有卷褶伪影残留，重建效果欠佳。这对于磁共振三维采集、动态成像、实时成像以及快速成像而言,提高GRAPPA算法是一个亟需解决的问题，本文提出一种基于奇异值分解(Singular Value Decomposition,SVD)算法来改变GRAPPA算法中的权重计算方式，以此降低矩阵维度、降低计算权重方程的条件数，增加权重的稳定性，提升计算速度，提高多倍降采样的情况下的图像重建质量。

GRAPPA算法有着更好的鲁棒性，对成像物体的运动不敏感，但GRAPPA算法中对多通道线圈的权重计算要求较高，其精确性关系到重建结果的质量。近年来并没有提出新的针对平面内的GRAPPA算法的改进算法，大量的带有GRAPPA、SENSE关键字的算法如slice-GRAPPA、split-slice-GRAPPA等算法都是进行同时多层成像的技术方法[5]，是基于GRAPPAS算法的核心层面思想在层面方向进行加速的算法，与平面内的并行成像算法GRAPPA并非相同用途。也有在平面内非笛卡尔采集方式(如radial、spiral等采集方式)下应用GRAPPA的研究[6-7]。本文提出的优化方法在普通的笛卡尔采集方式下即可完成，它在运用GRAPPA算法计算时对数据量进行优化和降维，虽然增加了算法复杂度，但它对参与计算的数据量进行了缩减，减少了计算时间，且不降低计算的精度，还提高了GRAPPA算法的重建效果，是更底层的算法改进。有报道提出关于GRAPPA的优化算法，例如采用伪随机采样模板进行欠采样[8]，在拟合的过程加入正则项进行权重的计算[9]等，其中最有效的步骤仍然是基本的GRAPPA算法。

1 计算方法与数据收集

1.1 GRAPPA算法求解

GRAPPA算法在全采样数据ACS计算权重，在非ACS信号欠采样数据获取的条件下拟合欠采样数据点的值，K空间数据欠采样与计算权重拟合欠采样数据点的过程如图1所示，利用ACS信号对欠采样数据进行权重求解[10]：

sn(kx,ky+rΔky)=

(1)

式中：(kx,ky+rΔky)为未采样数据的坐标，r为采集点到前一已采集点的偏移量，r=1,2,…,R-1；R为欠采样倍数，也是后面提到的加速倍数；Δkx、Δky分别为x、y方向的单位偏移量;l为线圈索引;L为线圈数;h为x方向索引；H1、H2为x方向插值窗界限；t为y方向索引；N1、N2为y方向插值窗界限；wj, r(l,h,t)为第l个线圈插值窗内的已采样数据权重值。

图1 K空间数据欠采样与线性拟合欠采样数据过程

设第ki行为n行线圈ACS采集数据，第n个欠采样数据Dn(ki)可以写成求和的形式:

(2)

式中:w(k)为权重数据;D(k)为采集数据;Dn(ki)为欠采样数据插值目标点;kernel为插值窗内的已采样数据点的集合。根据已采集数据D(k)及其权重w(k)来估计，上述计算权重w(k)的过程变成矩阵求解过程，Dn(ki)为列向量T，D(k)为矩阵S，w(k)为矩阵W，上式转换为：

SW=T

(3)

对于不同的插值窗，预测单个未采集数据点所需要的源采样数据点的个数

N=L(H2-H1)[(N2-N1)+1]

(4)

如果采集的ACS行的数据个数为Y，则S矩阵是Y×N矩阵，向量T的长度是Y。由GRAPPA算法采样及权重计算过程可知，S矩阵为梯度线圈采集的K空间数据，根据权重矩阵大小和ACS的数量不同，大多数情况下S的每个单线圈权重计算不是一个方阵，所以式(3)是一个超定方程，GRAPPA算法的权重矩阵W使用普通最小二乘法求解得到：

W=(SHS)-1SHT

(5)

式中:SH是S的共轭转置，(SHS)-1是对(SHS)求逆矩阵。普通最小二乘法有两个基本假设是：①S非奇异或者列满秩;② 向量T或者矩阵S存在加性噪声[11]。但在工程应用中，采样数据间相关性很强，矩阵S无法做到列满秩，因此GRAPPA算法很难得到最优解，即使调整插值窗也难以解决秩亏缺。SHS矩阵的条件数:

cond(SHS)=[cond(S)]2

(6)

S的误差δS和T的误差δT对W的误差δW的影响与S的条件数的平方成正比，影响到整个权重值求解[12]，权重值的计算精度降低会直接影响插值的准确性，降低重建后的图像质量。

1.2 基于SVD的GRAPPA方法

为解决在其采样数据后，多倍降采样数据在采样及计算过程中出现的噪声及计算权重的超定方程病态问题，引入奇异值分解方法(Singular Value Decomposintion Technique，SVD)[13-15]，在降低权重维度，提高采样倍数情况下，同时降低采样时间，提高采样效率，提升重构图像质量。

基于SVD的GRAPPA算法步骤：

(1) 将图像进行多倍降采样，如图1所示，将已采集到K空间数据与ACS进行线性加权拟合，用SVD计算得到各线圈权重系数；

(2) 利用权重系数和已采样K空间数据计算欠采样数据；

(3) 对完整K空间数据进行傅里叶逆变换，重构各个线圈图像；

(4) 将各个线圈图像整合为一张输出重构图。

采样矩阵S为奇异阵，由SVD方法，将矩阵S进行奇异值分解[16]：

S=UΣVT

(7)

(8)

故最小的奇异值σmin会增大条件数，出现比较大的扰动。因此需要计算超定方程的有效秩r，可以采用归一化奇异值的方法

σmin/σmax>ε

(9)

选择一个阈值ε，ε是某个很小的正数，例如可以选择ε=0.1，对较小奇异值进行截断。舍去小于ε的奇异值及其对应特征向量，相当于舍去了相关性较强的向量，降低了条件数。

利用压缩后的矩阵再对降采样缺失行进行填充，其间仍采用最小二乘法式(5)求解，获得完整的K空间数据。

1.3 数据收集

实验验证过程中的验证数据来自ALLTECH 1.5T磁共振扫描系统获取的8通道头线圈的全部原始数据(raw data)，采用梯度回波脉冲序列(Gradient Echo Pulse Sequence，GRE)，脉冲序列的参数信息为：回波时间，TE=9 ms，脉冲重复时间，TR=143 ms，水脂偏移系数，Water Fat Shift=0.8，矩阵大小为256×278。数据采集方式如图1所示,并行磁共振成像沿着相位编码方向上，以加速因子R进行周期性轨迹采样。将相应相位编码行进行置零以模拟降采样过程，保留K空间中间低频部分行作为计算卷积核权重的ACS部分。完全采样的K空间数据重建出的图像作为对比参考图像。

本文将对加速因子R为2～5这4种情况进行数据降采样，K空间低频部分ACS部分取16和32两种情况，为提高采样时间，减少采样引起的运动伪影，大部分ACS取16。根据采样数据，将对文中所描述的改进算法进行图像重建，与传统的GRAPPA算法图像重建进行对比分析,图像重建仿真计算在Matlab软件上进行。

1.4 算法评价

为评价改进算法在并行成像多倍降采样下重构图像质量，从图像重构质量与算法运行时间评价算法优劣。

图像质量主要从改进算法重构图像与传统算法重构图像进行分析，将重建后的图像与全采样图像进行比较，分别生成改进算法与传统算法差异十倍显示比较图，改进算法与全采样重建图像误差图，传统算法与全采样重建图像误差图。

时间评价算法采用卷积核权重算法时间及算法重建时间作为评价标准。

2 结果分析

2.1 图像结果分析

本研究用8通道全采样头部图像作为算法重建过程对比标准图如图2所示，实验分别用加速因子R为2～5，ACS线为16、32进行图像传统算法与改进算法SVD+GRAPPA重建。图3所示为在不同采样条件下的改进算法SVD+GRAPPA、传统GRAPPA算法重建图与误差图，该误差图为两种重建算法差值放大10倍后的效果图。

图2 8通道头线圈全采样图像

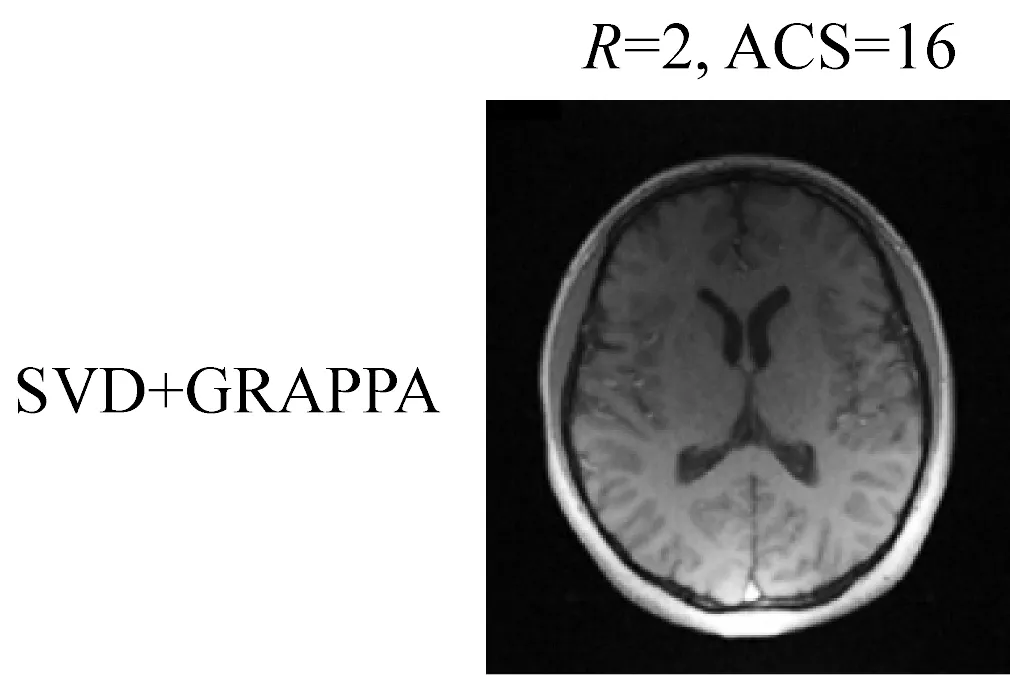
图3 在不同采样条件下改进算法SVD+GRAPPA、传统GRAPPA算法重建图与误差图比较

从图像上分析，当加速因子R=2，ACS=16时，改进算法SVD+GRAPPA和传统GRAPPA算法重建的图像几乎都能达到临床诊断效果，两算法间重建差异小。当加速因子R=3时，传统GRAPPA算法已经出现异常增亮影，即卷褶伪影。当R为5时，传统算法已经完全无法分辨大脑内部结构，白质和灰质为一整片区域，无密度比较。加速因子越大，传统GRAPPA算法中伪影越多，可识别组织信息越少，欠采样会导致数据采集完整性降低，传统算法欠采样程度越大，图像质量损失越严重。

改进算法SVD+GRAPPA重构图中，当加速因子为R=2，ACS=16时，改进算法重构图与传统算法差值图几乎为全黑图像，即两图无明显差异。当加速因子R=3、4时，改进算法重构图与传统算法差值图为非全黑图像，即两图具有明显差异，SVD+GRAPPA重构图有较为细致的解剖结构，未出现异常增亮影，有清晰的白质和灰质密度影。当加速因子R=5时，图像有较为模糊的解剖结构，出现噪声影，但相较于传统算法噪声量少。当加速因子R逐渐增大时，差值图像包含的信息量也越来越多，相较于传统GRAPPA算法，改进算法图像质量损失较少。

当R=4,ACS=16时，改进算法SVD+GRAPPA重构图像质量达到R最大化时，降采样重建效果最优。当R更大时，需增加ASC采样线，才能保证优质重构图像质量，可应用于临床诊断。

2.2 重建程序运算时间分析

重建时间为定量分析重要评价标准，主要从两方面分析，一是从卷积核权重计算时间上比较，二是从整个算法采集、权重计算、图像重建过程时间进行比较。

表1为改进算法SVD+GRAPPA与原算法GRAPPA卷积核权重计算时间比较，在 GRAPPA算法基础上解病态方程，相较于原算法来说，改进算法理论复杂度更高，但欠采样对矩阵进行压缩使得计算时间下降，运行效率更高。由表1可见，加速因子R=2、ACS=16时，改进算法比原算法用时减少79 ms，在原基础上效率提高39.6%，当加速因子为R=3时，改进算法用时减少67 ms，效率提高38.3%，当加速因子为R=4时，改进算法用时减少60 ms，效率提高38.6%。

表1 改进算法SVD+GRAPPA与原算法GRAPPA卷积核权重计算时间比较

表2为改进算法SVD+GRAPPA与原算法GRAPPA在图像采集、权重计算及重建过程等MRI并行计算整个过程时间比较。由表2可见，加速因子R=2、ACS=16时，改进算法比原算法用时减少0.61 s，在原基础上效率提高了51.3%，当加速因子R=3时，改进算法用时减少0.48 s，效率提高49.6%，当加速因子R=4时，改进算法比原算法用时减少0.49 s，效率提高53.4%。

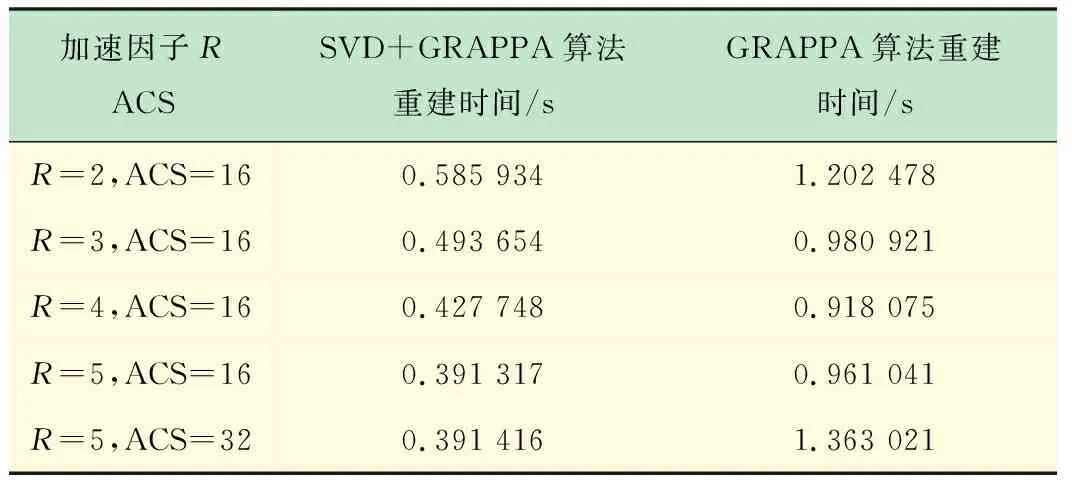
表2 改进算法SVD+GRAPPA与原算法GRAPPA重构时间比较

3 结 语

GRAPPA方法基于K空间，利用多通道相位控阵线圈冗余数据还原未采样数据行，其插值权重计算的准确性对重建算法的结果至关重要。原GRAPPA算法采用最小二乘法，但未考虑采样矩阵中向量的相关性问题，导致算法对插值窗大小和自动校准线数量的选取非常敏感，在加速因子R为3、4时，重建效果不佳。本文提出基于奇异值分解的自校准并行采集成像方法，相比传统算法更多的考虑了各已知采样数据向量之间的相关性。算法计算采样矩阵的奇异值后，去掉部分较小奇异值以达到降低条件数的效果。

实验发现改进算法相比原GRAPPA方法在加速因子R=3、4时表现出更细致的图像信息，能更好地分辨出大脑组织解剖结构。同时，MRI对人体部位扫描一次需要花费很长一段时间，肺部或心脏等部位的运动会降低图像质量，改进算法增加采样倍数同时优化重建图像算法，减少受检者检查时间。实验表明，基于奇异值分解的改进算法重建效果优于原GRAPPA方法。