DCO-OFDM系统中BPNN信道估计方法

李晓记， 高 天， 阎威龙， 杜卫海

(桂林电子科技大学 a.认知无线电与信息处理教育部重点实验室；b.信息与通信学院，广西 桂林 541004)

0 引 言

由于可见光具有丰富的频谱资源、极强的保密性能以及兼具照明与通信的特性，其一经问世便受到了广泛的关注[1]。1963年，随着水下光学透射窗口的发现[2]，激起了人们探索水下无线光通信的热情。但是，可见光信道的特殊性[3]以及水中阻挡物引起的多径效应都会造成传输信号的非线性失真，同时发光二极管(Light Emitting Light，LED)、功率放大器及光电二极管等器件的非线性特性[4]都会严重影响系统的通信性能。非线性失真逐渐成为扼制可见光高速传输系统发展的瓶颈[5]。机器学习问世以来，已被广泛应用于自然语言处理、计算机视觉、模式识别、生物信息学和化学等一系列领域[6]。在5G蓬勃发展的今天，将机器学习应用于通信，对于迎接处理海量通信数据的挑战具有重要意义[7]。

近年来，有很多学者利用机器学习在解决非线性问题方面的优势，将其应用于信道估计。研究表明，神经网络可获得比传统信道估计算法更好的估计性能。Ye等[8]提出了一种端到端的信道估计方式，将信道视为黑盒，通过深度神经网络拟合输入与输出之间的复杂映射模型，可直接在接收端恢复出发送的已调信号。Chi等[9]将高斯核函数引入深度神经网络后均衡器，在有效补偿水下可见光通信信道带来的非线性失真的同时，也减少了网络训练的迭代次数与时长。Amirabadi等[10]首次将深度神经网络(Deep Neural Networks，DNN)运用于在双伽马大气湍流环境下的自由空间光通信中。通过仿真验证了DNN通过训练迭代不仅能有效减少大气湍流效应对传输可靠性的影响，而且在不同大气湍流情况下都能表现出较强的鲁棒性。Lu等[11]设计了一个包含信道分类、信道估计以及信号检测功能的深度神经网络，用于在水下可见光通信(Underwater Visible Light Communication，UVLC)系统中的在线信道分类以及数据恢复。Lu等[12]提出了一种辅助核函数的长短期记忆神经网络后均衡器，以减轻可见光通信系统中由脉冲振幅调制(Pulse Amplitude Modulation，PAM)带来的非线性效应。

在直流偏置光正交频分复用(Direct-Current-Biased-Optical Orthogonal Frequency Division Multiplexing，DCO-OFDM)系统中，为达到驱动LED的条件，需对叠加完直流偏置后仍为负值的信号进行削波操作，这会导致部分信息的丢失，造成非常严重的非线性失真[13]。因此本文将后向传播神经网络(Back Propagation Neural Network，BPNN)信道估计方法应用于DCO-OFDM的水下可见光通信系统中，以消除通信系统中非线性失真带来的影响，提高系统性能。

1 水下可见光信道模型

Ma等[14]考虑到在整个光波频谱中，可见光在水下的衰减系数β(f)与其频率f的关系很难用闭式解析式表达，但在实际使用的频带宽度内，可将衰减系数与频率看成线性的关系，因此在Kaushal等[15]的基础上将水下可见光信道频域响应建模为

(1)

式中：L为路径的数量；α为衰减因子，与频率无关；β1和β2均为线性因子；f表示光信号频率；s表示光信号传输的距离；sl为第l条路径下光信号传输的距离；c0表示光速；sl/c0表示第l条路径的时延。

2 BPNN信道估计算法

2.1 基于BPNN的水下可见光通信系统模型

目前常见的水下可见光通信系统有非对称限幅光正交频分复用(Asymmetrically-Clipped-Optical Orthogonal Frequency Division Multiplexing，ACO-OFDM)系统以及DCO-OFDM系统，由于DCO-OFDM较ACO-OFDM拥有较高的频谱利用率以及较高的传输速率[16]，要适用于水下高速通信。因此本文选用DCO-OFDM系统来进行信道估计方面的研究。

驱动LED的信号为非负实数，而传统正交频分复用(OFDM)系统输出的是双极性复数信号，其次由于光强不能为负值的特性，导致其无法承载双极性信号，因此若要将OFDM技术应用于水下可见光通信，需对其进行改进。

为了使快速傅里叶逆变换(Inverse Fast Fourier Transform，IFFT)变换后得到的数据为实数，需对正交振幅调制(Quadrature Amplitude Modulation，QAM)后的数据进行厄米特对称变换：

(2)

式中：X表示QAM映射后的数据；X*为X的厄米特对称。虽然通过厄米特对称变换使得IFFT后的数据为实数，但其仍具有双极性，因此还需加上直流偏置，并对仍为负值的信号进行削波操作使其变为正实数信号。

直流偏置的大小通常设置为

一般常数μ的取值为2.05，经过处理后得到的数据为基于BPNN的DCO-OFDM系统模型如图1所示。

(3)

图1 基于BPNN的DCO-OFDM系统模型

在实际运用BPNN进行水下可见光通信信道估计时，将整个估计过程分为离线训练及在线估计两部分。离线训练时，用Matlab生成发送信号，让其通过水下可见光信道，在接收端得到接收信号，通过LS估计算法获得初步估计值后，将其拆分成实部和虚部再送入搭建好的神经网络进行拟合训练，随着神经网络参数的迭代更新，网络的输出数据会越来越接近所设定的标签值，待训练完成后，将训练得到的模型应用于在线估计。

2.2 BPNN原理

将神经元进行平行与垂直的组合后构成了神经网络，按照位置可将其划分为输入层、隐藏层以及输出层。图2所示为一个3层神经网络模型。

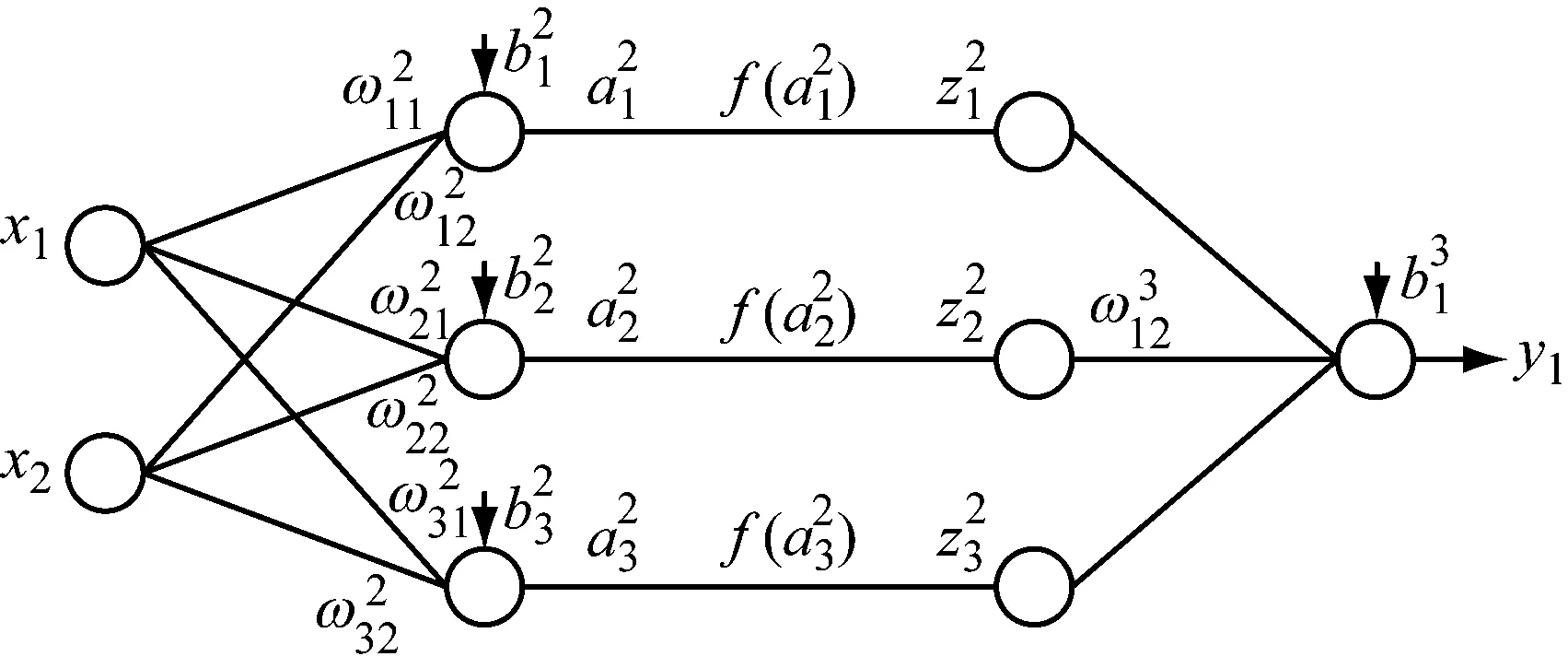
图2 3层神经网络模型

(4)

式中，f(x)为激活函数。本文选用的激活函数为Sigmoid函数，其表达式如下：

(5)

BPNN是利用梯度下降算法不断迭代优化其网络内部参数，直至损失函数最小化的多层前馈神经网络。本文选用均方误差损失函数，其表达式为

(6)

接着再由误差根据最速下降法的准则沿着网络逐层反向进行权值与偏置的调整，如此循环往复，直至误差达到设定的预期值，便完成网络的训练。根据最速下降法，应计算误差对权值ω的梯度∂E/∂ω，再沿着该方向反向进行调整。即更新后的权值为

(7)

同理，可求得更新后的偏置为

(8)

式中，η表示为学习率。

2.3 基于BPNN的信道估计器结构

在可见光通信系统中，LED、光电二极管、功率放大器等器件带来的非线性效应，以及吸收、散射、多径等因素会限制传统估计算法性能，导致估计精度并不理想。因此若将机器学习应用于水下可见光信道估计，可依靠神经网络在解决非线性问题方面的优势和潜力，拟合出光信号在水下的非线性传输特性，以进一步提高LS算法的估计精度。基于BPNN的信道估计器结构示意图如图3所示。

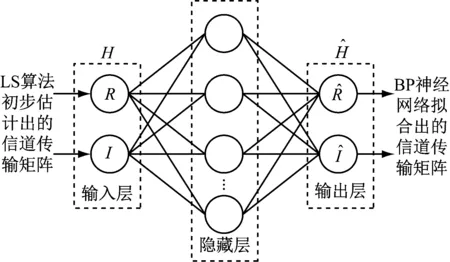
图3 3层神经网络信道估计器结构示意图

网络的输入值为LS算法估计得到的信道频域响应，其估计值具有复数特性，但神经网络不支持直接输入复数，因此将信道频域响应进行实部和虚部的拆分，以实数的形式输入。经过神经网络不断地迭代，损失函数值不断的逼近容许误差，当训练结束，将网络输出估计得到的实部以及虚部进行结合，转置还原成信道传输矩阵，再对接收信号进行信道均衡操作。

2.4 BPNN训练流程

整个训练流程为：先在发射端插入导频符号，经过信道后，在接收端提取导频符号，通过LS算法初步估计得到信道传输矩阵，接着取信道传输矩阵的实部和虚部作为数据的两个特征，建立数据集，并以4∶1的比例划分训练集和测试集，再对其进行归一化处理后，送入神经网络进行训练。当网络的输出值和信道真实传输矩阵的差值满足设定的预期值后，结束训练，否则继续训练。训练流程框图如图4所示。

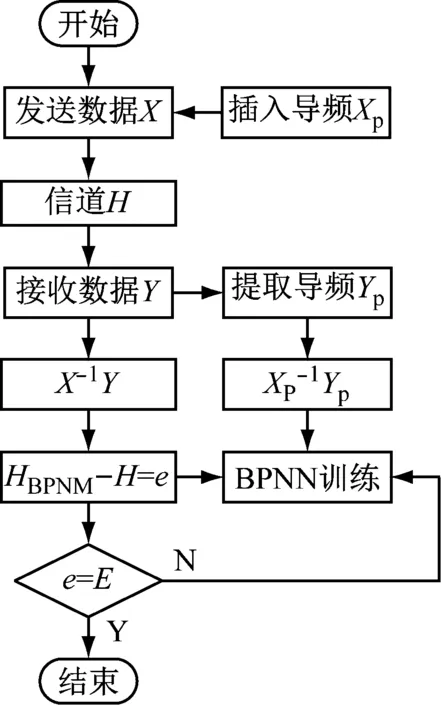
图4 BPNN估计流程框图

3 实验结果与分析

3.1 不同路径数量对算法性能影响的测试

本文首先在不同路径数量下对LS、BPNN、线性最小均方误差(Linear Minimum Mean Square Error，LMMSE)算法进行误比特率仿真对比。采用的调制格式为16QAM，导频插入方式为梳状结构，导频间隔为7，隐藏层神经元个数为15，学习率设置为0.5。仿真结果如图5所示。

(a) L=1

仿真结果表明：当仿真环境为单径时，由于在低信噪比(Signal Noise Ratio，SNR)下受噪声影响较大，使得BPNN和其他两种估计算法的系统BER曲线几乎完全重合。随着SNR的增加，3种算法误比特率皆呈下降趋势，其中BPNN算法误比特率下降程度高于LS算法。当SNR>30 dB后，在误比特率相同的情况下，BPNN信道估计算法较传统LS算法可获得1～2 dB左右的增益。而当SNR为35 dB时，BPNN算法可获得与LMMSE算法相同的估计精度。当径数L增加至3时，系统整体性能变差，BPNN较传统算法提升效果并不明显。虽然LMMSE算法估计精度高于BPNN算法，但是该算法不仅具有较高的复杂度，并且需要获取信道的先验信息，在实际应用中存在诸多限制，而BPNN算法则无需获取信噪比及信道模型，受限程度小。

3.2 不同传输距离对算法性能影响的测试

为进一步验证算法的可行性，本文利用实验室已搭建好的可见光通信系统测试平台进行算法验证[16]。系统的关键参数如下：LED功率为1 W，功率放大器增益为25 dB，数据子载波数为63，IFFT/FFT点数为128，OFDM符号数为15，DAC分辨率为14 bit，ADC分辨率为12 bit。

实际测试环境为清水，采用16QAM调制，将BPNN估计算法与传统LS算法比对。首先将收发机之间的初始距离设置为1 m，之后发射机以0.2 m为间隔，每次发送10帧信号，并以其中8帧信号作为训练集，剩余2帧信号作为测试集。实验结果如图6所示。

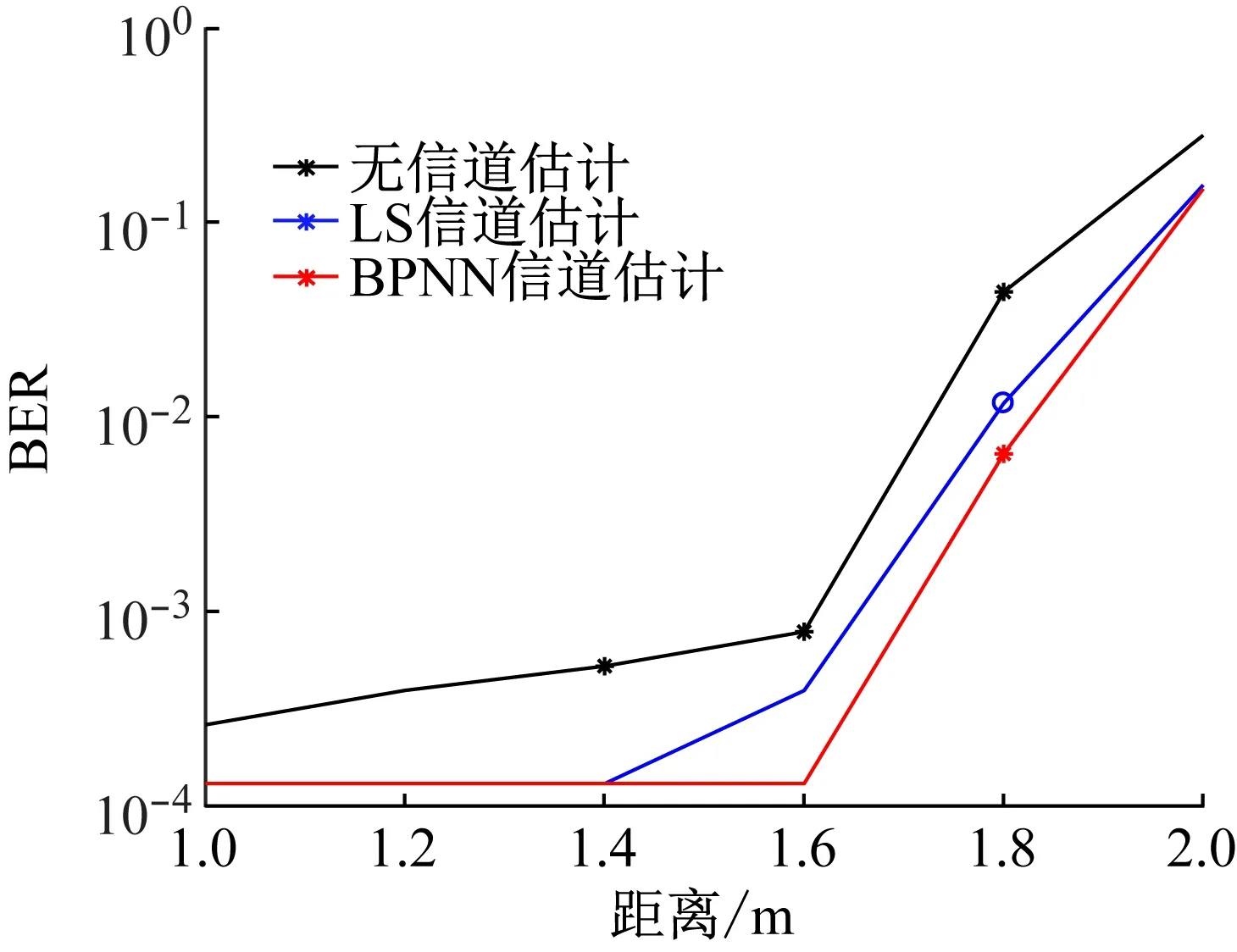
图6 不同距离下的误比特率曲线

当传输距离在1.4 m时，由于受到FPGA存储资源的限制，接收端接收到的两帧信号比特数为7 560，因此BPNN算法与LS算法的误比特率均为最低的1.32×10-4；当距离增加到1.6 m时，LS算法的误码率升至为3.97×10-4；当传输距离为1.8 m时，系统性能急剧下降，在无信道估计下的误比特率约为4.4×10-2，虽然使用传统LS算法使得误比特率有所下降，但仍然在10-2量级，而使用BPNN算法，则能使误比特率降至10-3量级。当传输距离为2 m时，受实验室系统及器件限制，LS算法及BPNN算法皆无法准确估计。综上所述，在近距离下，BPNN和LS算法都能取得较好的估计精度，当传输距离增加至1.6及1.8 m时，BPNN的误比特率皆低于传统LS算法，验证了将BPNN算法应用于DCO-OFDM系统进行水下可见光通信信道估计的可行性。

4 结 语

本文将BPNN算法应用于DCO-OFDM系统进行水下可见光通信信道估计，将LS算法的初步估计值输入神经网络，并以真实的信道频域响应值作为标签进行训练。通过神经网络拟合出非线性传输特性，以减少多径、削波及器件特性带来的非线性影响。本文通过仿真测试了在单径及3径条件下，BPNN、LS、LMMSE算法的估计精度。通过比较三者之间的误比特率曲线可以看出，低SNR时，三者估计的精度相当；高SNR时LMMSE算法最优，BPNN算法次之，LS算法最差。但因为LMMSE算法需先获取信道响应的自相关矩阵并在信噪比已知的条件下方可使用，这使得其不适用于实际系统，而BPNN算法则没有该限制。为进一步验证算法可行性，本文又通过DCO-OFDM可见光通信系统实验平台进行了在不同传输距离下的算法性能测试。结果表明BPNN算法可取得比传统算法更好的估计精度。