基于数据驱动的无车承运人平台线路定价策略研究

陈延展，陈少伟，胡 浩，任紫畅

(1.湖南大学 机械与运载工程学院，湖南 长沙 410082；2. 湖大艾盛汽车技术开发有限公司，湖南 长沙 410205 )

1 概述

无车承运人平台是基于大数据、人工智能和互联网等技术构建的新型物流平台，是促进物流行业转型升级的重要利器。无车承运人平台在2016年投入试点后，交通运输部门公布的统计数据显示，与传统物流模式相较，无车承运试点企业的车辆里程利用率提高50%，交易成本降低6%～8%，司机月收入增加30%～40%，等货时间由2～3 d降低至8～10 h[1]。由此可见，拥有发达信息化网络的无车承运人平台，能够对社会上的零散资源进行系统地整合并集成，从而提高我国货运市场的整体运作效率。无车承运人平台有3个参与角色：平台、货主、承运人。其利用互联网平台连接货主和承运人;通过有效对接货主与承运商的需求并促使其交易，极大改善了物流业资源闲置率高的状况。如果平台指导价格科学合理，则能够促进货运任务快速成交，增加货运任务交易的成功率，货主、承运人、平台三方均能获益，从而提高平台运行的整体效率。因此，如何科学地对无车承运人平台货运任务定价，具有很强的研究价值和现实意义。

定价策略和定价方法是市场营销组合中一个十分关键的组成部分，在金融、食品、物流等各个领域都具有广泛的应用。刘秋华[2]等基于贝叶斯博弈理论，提出一种不完全信息市场交易下多个售电商博弈的定价模型，将售电商定价下用户的最优购电策略与选择决策信息反馈给售电商。石永强[3]等基于博弈论的思想，针对现实中制造商委托零售商回收废旧产品以再次加工的逆向供应链定价问题展开研究，构建了制造商主导的Stackelberg博弈分散式定价模型与合作博弈的集中定价模型，从理论上证明了合作博弈能够给供应链带来更多利润，同时也能让消费者获益。陈斐然[4]等基于多边市场理论构建了消费者、自媒体(内容提供方)和广告商三边用户的垄断自媒体平台广告定价模型，并考虑投资预算约束下平台分别对各边用户的最优定价策略与服务投资策略，从而分析平台决策者在不同情况的最优投资对象选择策略。随着大数据和人工智能技术的飞速发展，基于数据驱动的定价方法受到越来越多的关注。宁克南[5]等基于lightGBM机器学习算法，利用二手商品的历史成交价格数据给出新生个人商家在出售其二手商品时的推荐价格，为二手市场的定价提供指导和借鉴。石言[6]等针对国内商业银行在系统性风险约束下的风险定价问题，提出了一种使用蒙特卡洛方法的深度强化学习框架模型，实证结果表明，由深度强化学习智能体所运营的银行在面对不同金融事件所带来的系统性风险与人类专家对手时，能够做出合理决策，使该模拟银行能够在风险中生存并获得更好的综合收益。

无车承运人平台在我国尚处于起步探索阶段，参考文献较少，但基于普通公路货运定价已经有了一些相关研究。顾敬岩[7]等研究了我国公路货运价格的演化趋势，并提出了一些政策建议。王燕凌[8]通过数据统计，分析了我国公路货运市场的供求。陈艳静[9]分析了公路货运价格的影响因素，并给出了一些完善运价形成机制的对策和建议。冯芬玲[10]等分析了公路和铁路的货运价格和服务竞争，并建立了铁路货运和公路货运的Hoteling模型。随着我国无车承运行业的逐步兴起，一些学者也开始关注无车承运人问题，但大多数研究都是围绕无车承运模式的现状分析和业务发展，其中，研究无车承运平台对托运人和实际承运人用户定价的文献较少。王聪珊[11]等给出了一个多元线性回归模型，预测了平台货运定价。聂福海[12]等基于信息不对称理论，从博弈角度研究了平台的定价策略。这些研究均是利用传统建模方法解决无车承认人平台定价的问题，考虑到影响平台定价的因素较少，对于定价决策等基本管理环节也没有进行深入讨论。然而作为货运经营者，无车承运人平台需要介入货运交易并赚取货运差价，因此如何科学指定面向车主的货物托运价格就显得尤为重要，线路定价策略直接影响着平台经营绩效和货运市场运行效率。

基于此，本文以某无车承运人平台提供的历史订单数据展开分析，以无车承运人视角对货运线路的定价策略进行研究。该无车承运人平台面向承运端司机，将需要承运的线路任务以合理的定价发布到网络平台上供承运端司机浏览并决定是否承运该运输任务。本文利用XGBoost模型为无车承运人平台的订单进行定价决策，旨在促进无车承运人平台订单快速成交和降低相应的承运成本，使得无车承运平台的利润最大化。

2 数据处理与相关性分析

首先对历史订单数据集进行数据预处理，并通过定量分析方法分析主要特征与线路定价的相关性，初步确定影响无车承运人平台进行货运线路定价的主要因素。

2.1 数据预处理

本次试验利用某无车承运人平台提供的16 005个历史成功交易订单数据为数据集，其中每个订单包含16个原始特征，具体的特征变量如下：x1为总里程，x2为车辆吨位，x3为车辆长度，x4为线路价格，x5为计划时间，x6为实际时间，x7为地区类型，x8为调价比列，x9为交易时长，x10为目的网点，x11为始发网点，x12为线路编码，x13为分拨时间，x14为调整时间，x15为是否续签约，x16为打包类型。由于数据集的样本数和特征数过多，所以只在附录1展示了前20个订单的样本数据。通过观察发现原始数据存在数据异常，所以采用的数据预处理操作如下：①若特征的值全相同，无法体现不同订单的差异性，作删除处理；②针对某一特征中出现少量缺失值的订单，则采取均值插值补全的措施；③利用原始数据进行特征构造，包括相对时间和统计量特征的构造；④在异常数据剔除后，将所有离散数据进行one-hot向量编码处理，所有连续数据作归一化处理，最终用经过数据预处理后的数据集作为预测无车承运人平台定价的XGBoost模型训练集。

2.2 相关性分析

为了更准确地描述无车承运人平台进行货运线路定价的主要因素，采用相关系数来进行相关性分析。本文采用Spearman秩相关系数[13]，通过计算预处理后得到的16个特征与定价的相关程度大小来分析影响定价的主要因素。

Spearman秩相关系数是衡量2个变量依赖性的非参数指标。它利用单调方程评价2个统计变量相关性。Spearman秩相关系数公式如下：

(1)

对2个变量成对的取值分别按照从小到大顺序编秩，Ri代表xi的秩，Qi代表yi的秩，Ri-Qi为xi，yi的秩次之差。通过Spearman秩相关系数得到16个特征数与任务定价的相关系数，其中每个特征之间的相关系数矩阵如图1所示。

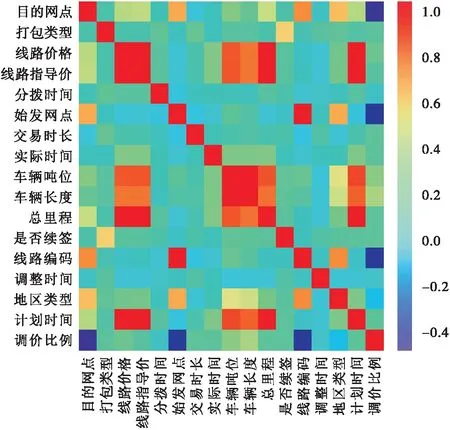
图1 各特征相关系数矩阵图

通过统计特征相关系数矩阵，做出各个特征与任务定价相关性大小的重要度排序表，见表1。根据表1可以发现在和任务定价的相关系数中70%以上的因素有总里程、计划时间、车辆吨位和车辆长度，由此可知这4个特征与无车承运人平台订单定价呈现强线性相关性。由于Spearman秩相关系数法只能作为线性相关度的评价指标，不能捕捉变量之间的非线性关系，所以更加准确的特征重要度排序需要通过XGBoost模型来实现。

表1 Spearman秩相关系数Table 1 Spearman’s rank correlation coefficients特征相关系数特征相关系数总里程0.991 118 ……计划时间0.973 576 线路编码-0.000 017 车辆吨位0.813 863 调价比例-0.204 449车辆长度0.765 718 打包类型-0.239 713线路价格0.419 636 始发网点0.102 90目的网点0.409 852 调整时间-0.106 65

3 模型应用与结果分析

本节旨在建立无车承运人平台的线路指导价格与订单16个特征变量之间的映射函数，而在训练数据中所有样本数据的线路指导价格均为已知，所以此问题是一个经典的有监督学习问题。目标订单的线路指导价格为连续变量，故基于机器学习的回归模型可以很好地完成这一任务。目前传统的机器学习算法例如线性回归、支持向量机和K近邻算法等对特征工程的依赖度极高，而且对于非线性程度高、内部规律较为复杂的映射关系的拟合能力有限。XGBoost 是一种集成学习的机器学习算法，通过构建多棵决策树来实现回归任务，将多个树模型组合在一起可以更加高效地学习到数据中的非线性关系。本节首先利用XGBoost预测出线路订单的线路指导价(即第1次报价)，然后结合第1次报价和调价策略制定出第2次和第3次定价，最终利用数据包络分析法对3次定价的结果进行评价，以证明预测模型和调价策略的合理性。

3.1 模型与算法介绍

XGBoost(Extreme Gradient Boosting)是由CHEN[14]等提出的一种支持并行计算的梯度提升树模型，近些年它凭借着突出的效率和较高的预测精度被广泛应用于Kaggle机器学习竞赛中。实际上XGBoost是一种改进的GBDT算法[15]，两者本质上均由许多用于回归和分类的决策树组成，但是XGBoost在以下方面对GBDT算法进行了改进：①对于损失函数，GBDT算法只使用了一阶泰勒展开，而XGBoost则增加了二阶泰勒展开；②XGBoost在目标函数中构造了正则惩罚项[16]以降低模型复杂度，从而防止模型过拟合。XGBoost模型的结构如图2所示，模型的细节如下所示。

图2 XGBoost算法示意图

对于一个给定的有n个样本的数据集D={(xi，yi)}，(i=1，2…，n)，则基于数据集D训练出的具有K个基学习器的XGBoost预测模型为：

(2)

F={f(x)=ωq(x)}

(3)

其中，f(x)表示模型的基学习器，F则表示基学习器的假设空间。在式(2)中q(x)表示第x个样本的叶子节点，ωq(x)则表示样本x的叶子分数，即模型的预测值。经过t次迭代后的预测结果如下：

(4)

在对训练数据进行学习时，每次在保留原有模型不变的基础上，加入1个新函数ft，观察对应的目标函数，若加入的新函数能使目标函数尽可能减到最小， 则把该函数加到模型中。此时目标函数表示为：

(5)

(6)

其中，L代表损失函数;Ω(ft)则表示模型的复杂度；T和ω分别表示叶节点数和得分。之后对目标函数进行二阶泰勒展开得到如下近似目标函数：

(7)

(8)

(9)

综上所述，最终求得的目标函数形式如下：

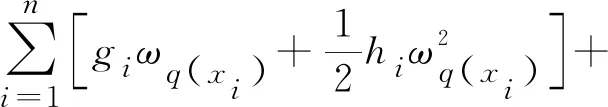
(10)

最后对式(9)中的目标函数进行优化，最优解为：

(11)

(12)

3.2 基于XGBoost的无车承运平台定价预测

本节以数据预处理后的货运线路已成交历史数据为训练集，分别采用多个机器学习模型对各个任务订单的线路总成本、线路指导价格和调价类型进行预测，并在测试集上利用各种评价指标进行模型对比。最后基于订单紧急程度制定了平台的调价策略，从而确定平台针对每个订单的3次定价。

3.2.1模型评价指标

(13)

(14)

(15)

3.2.2试验分析与模型对比

本文基于无车承运人平台历史订单数据集上分别训练了XGBoost定价预测模型和其它机器学习模型，如线性回归模型[17]、K近邻模型[18]、支持向量机[19]、决策树[20]和随机森林[21]等，表2提供了模型的简要说明。

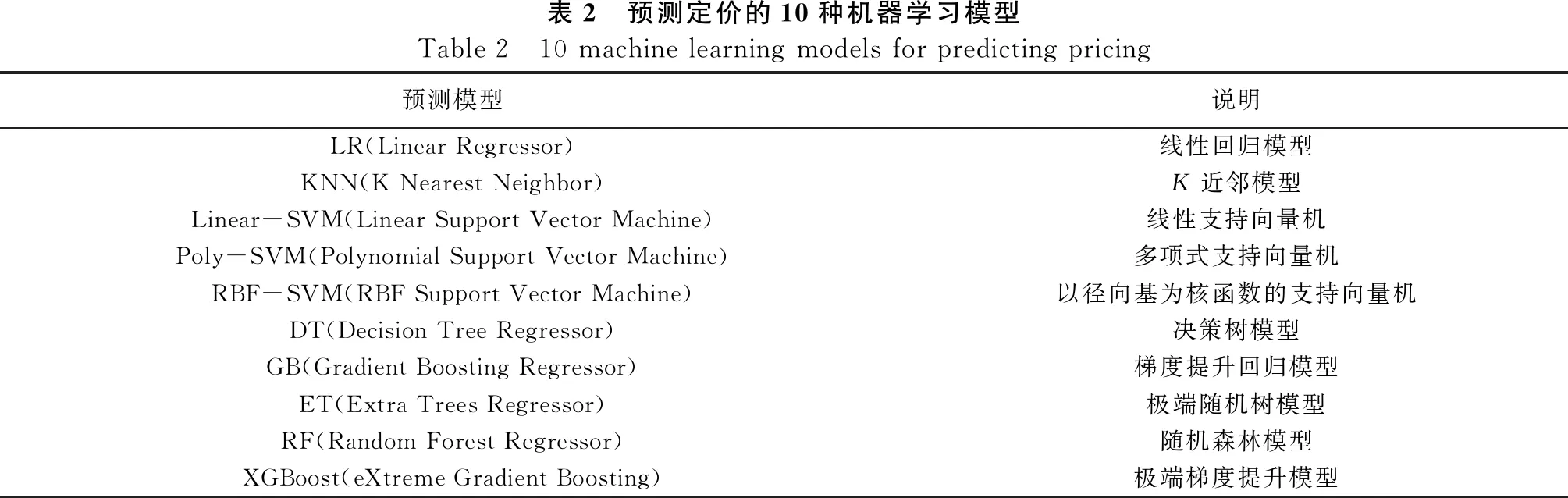
表2 预测定价的10种机器学习模型Table 2 10 machine learning models for predicting pricing预测模型说明LR(Linear Regressor)线性回归模型KNN(K Nearest Neighbor)K近邻模型Linear-SVM(Linear Support Vector Machine)线性支持向量机Poly-SVM(Polynomial Support Vector Machine)多项式支持向量机RBF-SVM(RBF Support Vector Machine)以径向基为核函数的支持向量机DT(Decision Tree Regressor)决策树模型GB(Gradient Boosting Regressor)梯度提升回归模型ET(Extra Trees Regressor)极端随机树模型RF(Random Forest Regressor)随机森林模型XGBoost(eXtreme Gradient Boosting)极端梯度提升模型

本次试验平台为AMD Ryzen 7 4800H with Radeon Graphics(2.90 GHz)，配置了16.0 GB的RAM内存和8 GB的GTX 1070Ti显卡。其中SVM、DT和RF等模型均在python的第三方库scikit-learn中实现。表3给出了上述10个机器学习模型对于无车承运人平台定价的预测精度、训练时间和测试时间。

表3 不同无车承运人平台定价预测模型的对比Table 3 Comparison of different pricing prediction models for NVOCC platforms预测模型R2MAERMSE训练时间/s预测时间/sLinear-SVM0.949 17.473 820.402 15.901 70.753 9LR0.951 26.920 919.040 70.869 10.012 2DT0.957 45.504 518.510 10.336 20.012KNN0.966 95.072 016.655 50.117 50.125 3Poly-SVM0.973 84.863 416.113 95.860 70.842 5GB0.977 94.222 315.448 81.273 20.101 2ETR0.986 64.188 414.882 40.420 40.020 2RBF-SVM0.989 43.949 614.320 17.356 21.847 5RF0.992 33.642 713.974 22.340 20.051XGBoost0.998 13.581 213.196 71.820 20.015 6

根据表3绘制出以上机器学习模型对于平台定价预测的R2、MAE和RMSE分布曲线，见图3。通过观察图3中的曲线可知，后7个模型的R2值均超过0.95而具有很高的预测精度，并且其中3个模型(RBF-SVM、RF和XGBoost)的R2值均高达0.99左右，远超其它模型。表现最为突出的XGBoost模型R2值更是高达0.998 1，并且MAE和RMSE值均处在所有模型的最低值。3种线性模型(LR、Poly-SVM和Linear-SVM)的预测精度都很差，其R2值均处在0.98以下，证明了平台定价与16个特征之间存在明显的非线性关系。其它3个模型(KNN、GB和ET)的预测精度则处于中等水平。

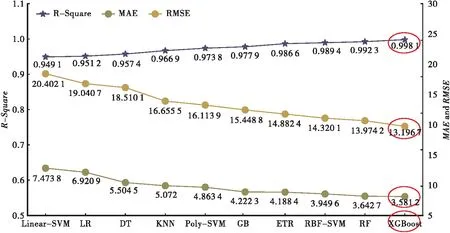
图3 不同无车承运人平台定价预测模型的评价指标对比图

为了进一步说明XGBoost模型的拟合效果，图4绘制了测试集数据中订单定价的真实标签值与XGBoost模型预测值之间的散点分布图。散点越接近直线则表示模型的预测能力越强。从图4可以直观看出该模型具有良好的定价预测能力。

图4 XGBoost模型预测值与真实值的散点图

综上所述，XGBoost模型的R2值最高，并且训练时间、预测时间、MAE值和RMSE值均相对较小。所以XGBoost模型在预测无车承运人平台的问题上比其他模型更加有效，本文最终采用XGBoost模型预测无车承运人平台定价。为了进一步研究每个特征对平台定价的影响，基于XGBoost模型计算了16个特征的相对重要度，对影响平台定价16个特征的重要度进行降序排列,见图5。

上文2.2节中的Spearman秩相关系数只能用来衡量2个连续变量之间的线性关系强弱程度，而XGBoost模型的特征重要度大小则是根据特征在提升决策树构建中的贡献度来确定的，由特征在每个分裂点的Gini纯度计算得出。因此基于XGBoost的特征重要度排序可以挖掘出定价与特征之间的非线性关系，其结果也更加准确可靠。由图5可知，总里程、车辆吨位和车辆长度的重要度贡献率较高，而其它特征(交易时常、调整时间和分拨时间等)则对平台定价的影响较小。现实生活中线路总里程是任务价格的直接影响因素，路程越长，成本越高，相应定价也会越高。车辆吨位和车辆长度是车辆型号和载重的衡量指标，吨位和长度越大，货车的载重越大，相应价格也越高。由此可知，总里程、车辆吨位和车辆长度是影响线路定价的最重要的特征变量。

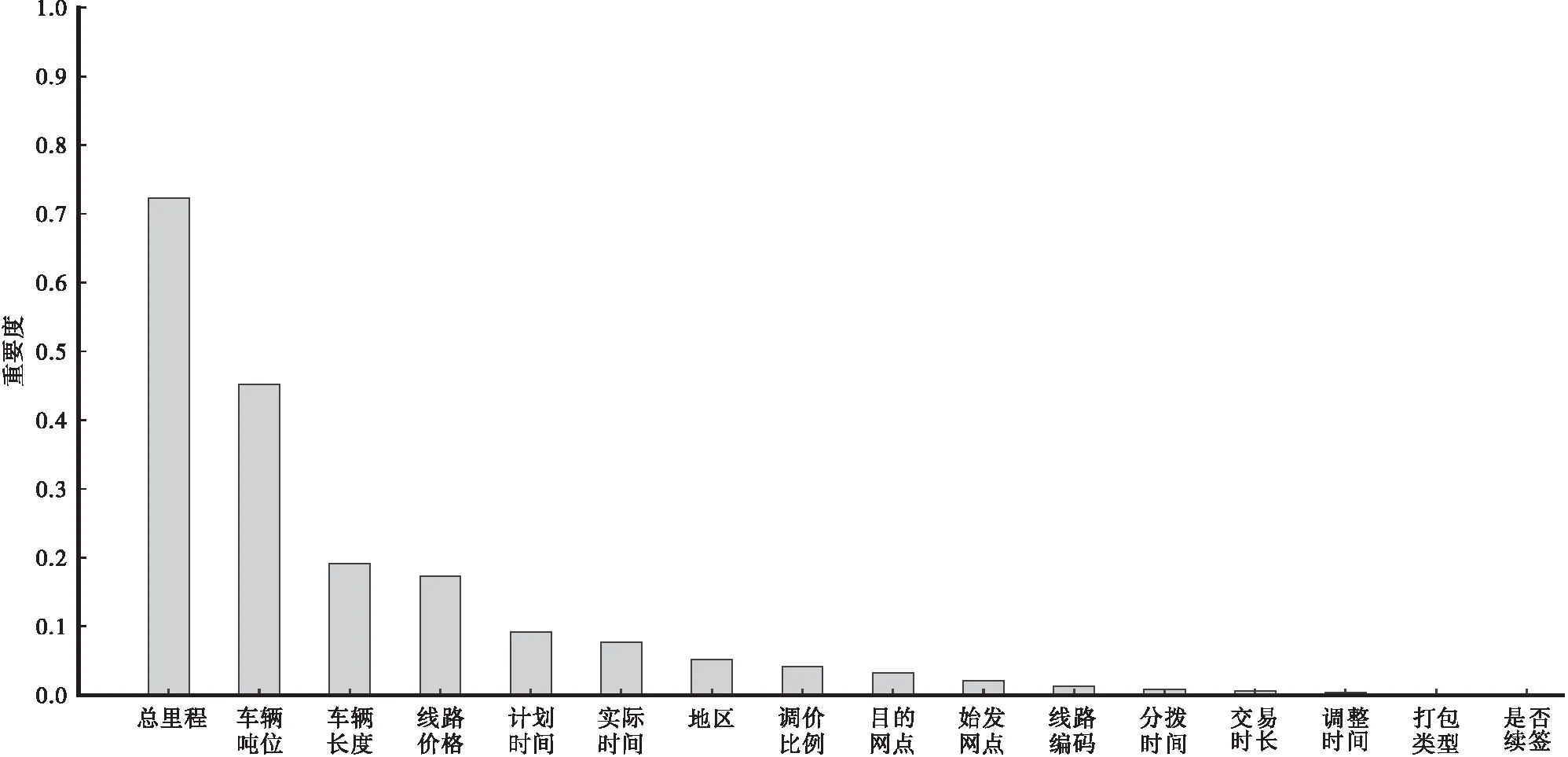
图5 影响平台定价的特征重要度排序

3.3 调价策略

为了保证无车承运人平台每个订单任务都尽可能被承运，平台采取动态定价的形式保证总收益最大化。若在给定的时间内，该任务没有司机接单，则该线路 就可以进行调价。假设每条线路任务最多允许发布 3 次价格，即首次发布线路价格后仍可刷新2次线路价格。由于平台的目标是整体盈利，部分订单成交价格高于成本价，部分订单成交价低于成本价，订单的紧急程度会影响平台的调价策略。

首先根据数据集中各订单的需求紧急程度将订单分为“常规订单”(14 670个)、 “紧急订单”(330个)和“特急订单”(1 005个)， 根据式(5)分别计算3类订单的平均溢价比，以说明不同紧急程度的订单调价的一般水平：

i=1，2，3

(16)

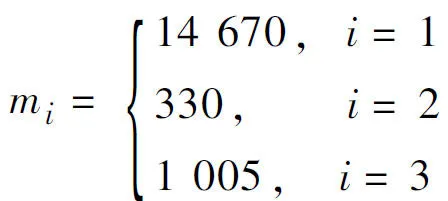
(17)

其中，ai表示第i类订单的平均溢价比，mi表示第i类订单下的样本数，i=1，2，3 分别表示常规订单、紧急订单和特急订单。最终确定的定价策略如下：根据XGBoost模型的预测结果，确定各个订单的调价类型，针对常规订单，第1次报价为订单的指导价格；针对紧急订单和特急订单，平台急于帮助货主找到承运司机，因此第1次报价为在订单指导价格的基础上，参考成本价、该类订单的一般调价水平进行调整。针对所有订单，第2次和第3次报价均是综合考虑指导价格、一般调价水平、调价类型(调高、 调低、 不调整)和成本后进行调整。调整策略见表4。

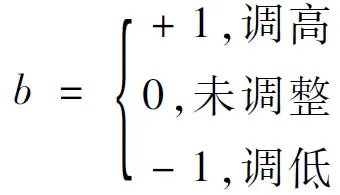
(18)

3.4 基于DEA的综合评价

为了验证上节调价策略的合理性，本节利用数据包络法对前1 500个订单3次定价的综合效率进行评价。数据包络分析[22](DEA)是根据多指标投入和多指标产出对相同类型的单位进行相对有效性或效益评价的一种系统分析方法，多用于处理多目标决策问题。数据包络法的具体步骤如下。

a.确定输出指标。

本文站在无车承运平台的角度，平台在当前阶段较为关注的目标是快速促进成交和较低的承运成本，因此其希望通过每单成交的时间更短、每单获得的利润更大，因此设“线路价格”为y1、 “线路指导价”为y2， 对变量x9“交易成功时长”按公式(19)计算得到y3“时间倒数”：

n=1，2，…，15 719

(19)

b.确定输入指标。

根据前文特征重要度分析的结果，“总里程”、“车辆吨位”、“车辆长度”、“线路价格”、 “计划时间”5个变量是各单定价的主要影响因素。因此假设仅有x1“总里程”、x2“车辆吨位”、x3“车辆长度”、x4“线路价格”、x5“计划时间”5 个变量同时会影响初始定价和最终成交价，因此选择上述5个变量作为输入变量。

c.建立 CCR 模型。

设DMUn表示第n个决策单元(n=1， 2， …， 16 005 )，每个决策单元都有5种投入量和3种产出量，设xi，n(i=1，2，3，4，5;n=1，2，…，16 005)表示第n个决策单位的第i种投入量，yj，n(j=1，2，3;n=1，2，…，15 719)表示第n个决策单位的第j种产出量，vi(i=1，2，3，4，5 )表示第i种投入的权重，uj(j=1，2，3 )表示第j种产出的权重。

向量Xn和Yn分别表示第n个决策单元输入向量和输出向量，V和U分别表示 输入指标的权重向量和输出指标的权重向量，设Xn=(x1，n，x2，n，x3，n，x4，n，x5，n)T，Yn=(y1，n，y2，n，y3，n)T，V=(v1，v2，v3，v4，v5)T，U=(u1，u2，u3)T。目标是少投入、多产出，决策单元n0率的模型为：

(20)

(21)

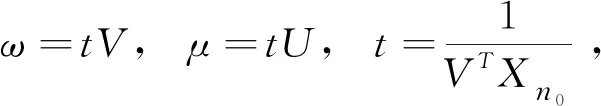
maxVn0=μTYn0

(22)

(23)

d.DEA评价结果。

针对选取的1 500个样本订单的1次报价、2次报价和3次报价的预测值，DEA评价结果如表5所示。针对1次报价，99.46%的订单的综合效率处于 0.8 至 1；针对2次报价，99.07%的订单的综合效率处于0.8至1；针对3次报价，78.07%的订单的综合效率处于0.8至1。综上所述，利用XGBoost模型的预测结果和定价策略相结合对订单3次定价进行预测，结果表明，大部分订单的定价结果符合平台现阶段目标。

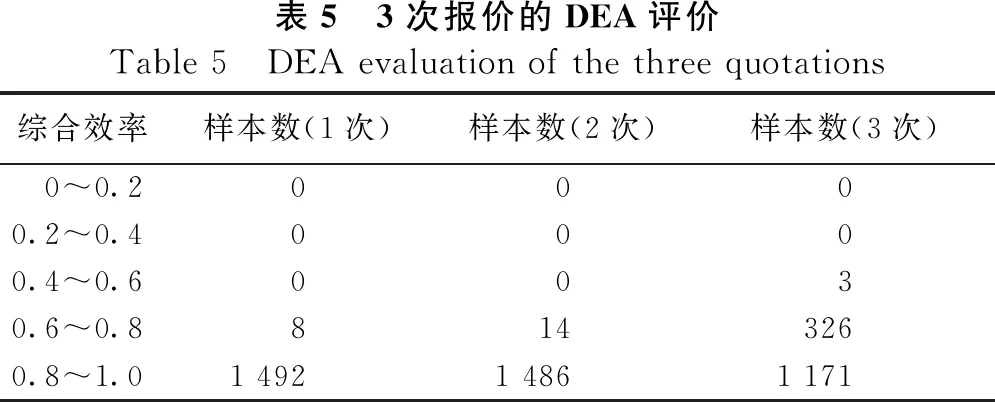
表5 3次报价的DEA评价Table 5 DEA evaluation of the three quotations综合效率样本数(1次)样本数(2次)样本数(3次)0～0.20000.2～0.40000.4～0.60030.6～0.88143260.8～1.01 4921 4861 171

4 结论

本文以无车承运人平台为研究对象，结合平台的大量已成交历史订单数据，构建了无车承运人平台线路定价的XGBoost预测模型，并且基于订单的紧急程度制定了无车承运人平台的调价策略，随后利用XGBoost预测模型和调价策略相结合预测出订单的3次定价数值，最后使用数据包络分析法对订单预测出的3次定价进行综合效率评价，主要得出以下结论：

a.通过对比XGBoost模型与其它9种机器学习模型在人工划分的测试集上对线路指导价的预测性能，证明XGBoost模型在无车承运人平台定价问题上的预测效果最优，并在XGBoost模型的预测结果的基础上制定了基于订单紧急程度的调价策略。

b.基于XGBoost模型计算了影响平台定价的16个特征的相对重要度，结果表明，“总里程”、“车辆长度”、“车辆吨位”、“线路价格”、 “计划时间”5个变量是各单定价的主要影响因素。

c.利用数据包络分析法计算出1次定价、2次定价和3次定价分别有99.46%、99.07%和78.07%的订单的综合效率处于0.8～1的区间，证明了本文XGBoost模型与调价策略相结合的定价预测方法的合理性。

本文研究为无车承运人平台的定价决策提供了有益借鉴和科学依据，但本文仅以无车承运人平台和承运司机为研究对象，没有考虑面向货主的运输任务的报价，未来的研究内容可以围绕上述内容展开讨论。