基于GPR三维正演技术的路面空洞含水率研究

束 裕，程博文，于晓贺 ，李 冲，罗 蓉

(1.武汉理工大学，湖北 武汉 430063；2.湖北省公路工程技术研究中心，湖北 武汉 430063)

0 引言

自20世纪80年代起步以来，伴随我国经济的增长，公路干线网迅速发展升级。随着公路总里程的增加，道路在表面和内部都将出现不同形式的损伤，如表面裂缝、车辙、基层反射裂缝和空洞等病害。相比较来说，路表病害比路面内部病害更容易被检测出来，但路面内部病害对路面造成损伤更大。路面含水空洞病害是路面早期水损害形式一种，其出现频率非常高，具有普遍性、难以发现等特点，常用检测仪器和评价指标体系无法判断其发展、影响程度。因此，需要一种有效检测手段来判定其损伤程度。

探地雷达(Ground Penetrating Radar，简称GPR)检测是一项用于浅层地质探测的新技术，又称为地质雷达，具有高效、简便、分辨率高、无损的特点。GPR图像正演技术是一种通过计算机模拟电磁波在道路介质中传播过程的方法[1]。通过模拟电磁波在道路沥青混合料介质的传播过程，可以提高对探地雷达探测剖面的认识，提高实际雷达检测数据解译、分析结果的准确性。

陶连金[2]等采用对离散元软件对城市道路地下空洞病害进行机理研究，从细观的角度揭示了地下空洞发展至路面塌陷的破坏机制；张青山[3]通过现场雷达检测与室内试验结合分析沥青路面水损害的状况，并提出分级养护措施；刘俊[4]采用二维时域有限差分法对路面雷达电磁波进行模拟，建立了路面脱空病害的二维正演模型；姜守东[5]等通过探地雷达对沥青路面内部的检测效果进行研究，发现探地雷达对材料的孔隙率和含水率反应强烈，对层间积水有良好的检测效果。目前研究均明确：路面中含水空洞病害对路面的影响较大，但由于路面含水空洞病害为路面内部病害，要实现准确测量其含水率比较困难。

经研究发现，含水空洞中的含水率与雷达波形图之间存在着定量关系。因此，本文通过分析实际雷达数据，建立不同含水率空洞模型，建立含水率与反射波形的数值关系，进而通过峰值反向计算空洞含水率，为分析典型病害发展趋势和高速公路预防性养护提供数据支撑，这对于精细化分析路面内部含水空洞病害等沥青路面早期水损害问题具有较大的实际工程意义。

1 理论推导

1.1 探地雷达在道路结构中的传播规律

在确定路面空洞含水率的研究中，构建典型病害识别图谱是第1步，而其基础便是通过程序准确模拟电磁波在三维介质中的传播过程。模拟电磁波在沥青混合料面层的传播过程则是通过有限元法求解基于电磁场参数的Maxwell方程组。

根据电磁波理论，高频电磁波在介质中的传播规律服从Maxwell方程组[6]，该方程组用于描述磁场和电场相互激发、相互联系形成电磁场中的关系，并结合介质的本构方程可得到式(1)。式(1)满足电磁波在介质传播规律，被称为电磁场的Helmholtz方程[7]。基于式(1)可知：①发射天线在沥青混合料中形成的电磁场以波的形式运动；②电磁波是可以脱离波源独立传播的。

(1)

式中：E为电场强度；H为磁感应强度；μ为磁导率，由于沥青混合料是非磁性路面材料，因此沥青混合料的磁导率μ为0；δ为电导率，其物理意义为沥青混合料中的自由电荷在外加电场作用下产生瞬变电流的能力；ε为介电常数，表示为沥青混合料在外部电场的作用下电能存储、损耗的能力。

1.2 激励源的设置

有限元模型的后续迭代计算需要选取合适的入射波与其数值变化规律。本文将选取1 GHz的雷克子波作为本次正演过程的激励源。雷克子波被广泛应用于地表浅层探测工作中。在实际检测过程中，初始场值始终为零，因此在雷达波数值模拟过程中，激励源的初始值为零。为使雷克子波波形的初始值为零，通常在时域中保持其频谱不变条件下，通过移动雷克子波来实现。延时雷克子波的表达式如下式所示[8]：

(2)

式中：t0代表延迟时间。一般认为t0=1/fm。

图1为探地雷达天线的中心频率为1GHz的雷克子波时域波形图。

图1 1 GHz雷克子波的时域波形图

1.3 三维GPR波动方程有限元求解

本文选取基于单行波算子的吸收边界条件(ABC)作为本文正演的边界条件。ABC吸收边界是通过在网格剖分外部添加一层具有与边界散射电磁波频率入射角无关的波阻抗的媒质。与传统的分裂式PML吸收边界条件相比，ABC边界具有计算量小，算法稳定和吸收效果好等优点，可以提高三维波动方程数值模拟的计算效率[9]。

本文将采用伽辽金法[10]推导电磁波在沥青混合料中探地雷达有限元方程GPR波动方程把场矢量随空间、时间的变化联系在一起，说明电磁场是以波动方式在空间的传播的。式(3)表示为GPR的波动方程的余量。

(3)

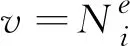
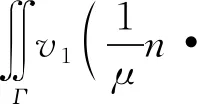
(4)

式中：R为加权余量;v和v1为权函数；n为电场的切线方向向量，公式中其他含义与上式相同。将公式(4)中的右边第1项展开为笛卡尔坐标系的表示方法，并利用函数乘积的分部积分公式进行化简得到式(5)：

(5)

将式(5)代回式(4)，选择试函数v=-v1，得到式(6)，再通过正六面体将三维区域划分成多个单元，得到单元矩阵方程。

(6)

假设网格区域有N个节点，采用六面体单元将计算区域进行结构化网格划分，设置插值函数后，进行化简，得到求解方程，再将方程进行扩展至整体区域、所有节点，得到式(7)：

(7)

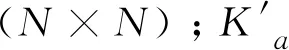
将式(7)采用中心差分法进行求解，得到可以依次递推电磁任意时间的电场值的式(8)：

(8)

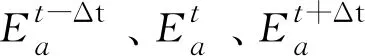
2 数据采集

路面结构层的厚度参数和混合料的相对介电常数是进行计算的重要参数。为了使构建的模型符合路面结构真实情况，保证验证计算模型的真实性，因此采用真实路面结构层的厚度参数构建模型，采用瑞利(Rayleigh)模型来计算相对介电常数。

秦明月正要犹豫着要不要告诉她所敬爱的毛德君已经死掉的事实时，正在检查办公室的赵大刚指着房间角落内一个纸箱说：“这是什么？”

本文的数据采集地点为湖北省汉十高速公路孝襄段，主要进行数据采集的3个部分：首先，通过探地雷达检测设备对汉十高速公路孝襄段进行雷达检测，以获取道路纵向雷达检测二维剖面图像和所有检测点的单道反射波形数据数据；其次，本文对汉十高速公路孝襄段开展钻芯取样工作，测量面层芯样结构层厚度，以建立更加符合实际路况的道路三维模型；最后，由于相对介电常数测量的不稳定性，本文需要通过计算模型进行计算混合料的相对介电常数。由于介电常数数值较大，并且难以准确得到，因此通常采用介电常数ε与真空介电常数ε0的比值表示，即相对介电常数ε1=ε/ε0。该参数是描述材料的极化特性的物理参数，即材料在外加电场的作用下，材料在电场中存储电荷的能力。

2.1 路面雷达检测

本次检测使用的是由武汉理工大学和美国德克萨斯农机大学联合开发的WB1-21型路用探地雷达检测设备，如图2所示。本文设计的探地雷达检测设备的参数如下：①工作频率：1 GHz；②探测深度：0～60 cm；③竖向分辨率0.1 mm；④发射点间距：0.5 m。由于探地雷达检测深度为60 cm，此次检测目标为道路面层和基层。并通过设备等距发射电磁波，接受道路反射的回波，以得到道路雷达检测数据。

图2 WB1-21型探地雷达检测装置

2.2 现场钻芯取样

路面取芯作为传统的检测手段，钻取的芯样不仅可以进行病害判断，还可以在路面使用中准确的得到路面各结构层的厚度，为后续建立道路三维模型奠定基础[11]。由于本文钻芯的目的是得到各结构层的厚度，因此本次所取芯样厚度为整个沥青面层。为了不影响高速公路的正常运营，本次取芯选择慢车道进行取芯，取芯过程如图3所示，一共取了8个芯样(见图4)，芯样的厚度数据如表1所示。2.3相对介电常数的计算

图3 汉十高速公路现场取芯

图4 现场芯样图

采用仪器所测量的相对介电常数具有不稳定性，因此采用计算的方法得到相对介电常数。本文采用的相对介电常数的计算模型为瑞利(Rayleigh)模型，该模型相对于线形模型、均方根模型等复合材料介电模型来说误差较小，比较适用于计算路面各结构层的相对介电常数[12]。

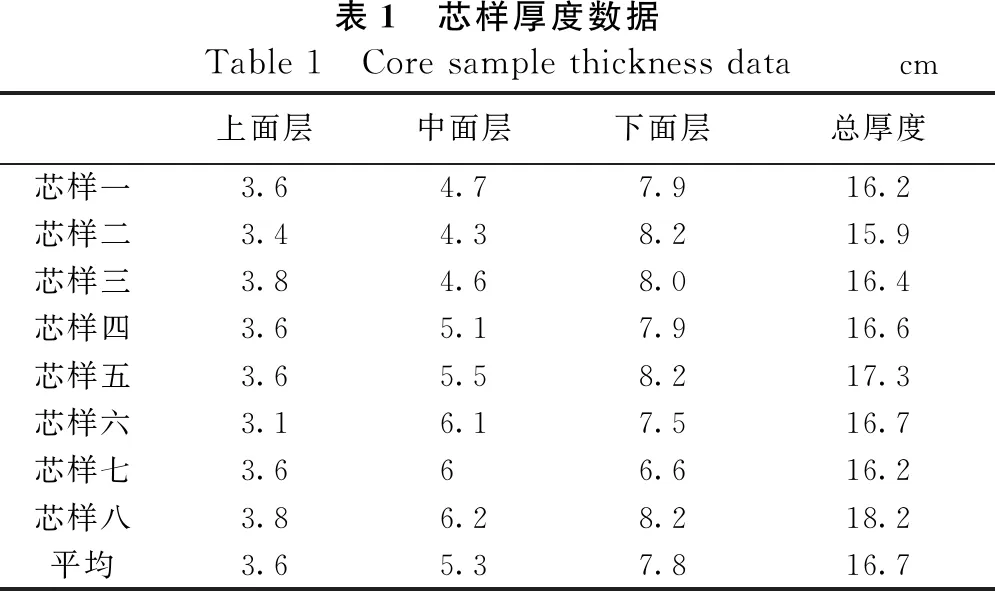
表1 芯样厚度数据Table 1 Core sample thickness datacm上面层中面层下面层总厚度芯样一3.64.77.916.2芯样二3.44.38.215.9芯样三3.84.68.016.4芯样四3.65.17.916.6芯样五3.65.58.217.3芯样六3.16.17.516.7芯样七3.666.616.2芯样八3.86.28.218.2平均3.65.37.816.7

沥青混合料是由空气、沥青结合料和骨料组成的三相复合介质，其瑞利(Rayleigh)模型可表示为：

(9)

式中：θa、θas、θs分别为空气、沥青、集料的体积率；εac、εa、εas、εs分别为混合料试件、空气、沥青、集料的相对介电常数。

表2为常用路面使用材料的相对介电常数值，表3为汉十高速公路孝襄段所取的芯样各结构层的材料体积率的平均值，将其代入到式(9)中，可以得到各结构层沥青混合料的相对介电常数。

表2 常用路用材料介电常数范围Table 2 Dielectric constant range of common circuit materials路面材料介电常数范围空气1水81沥青5.1石灰岩8.4

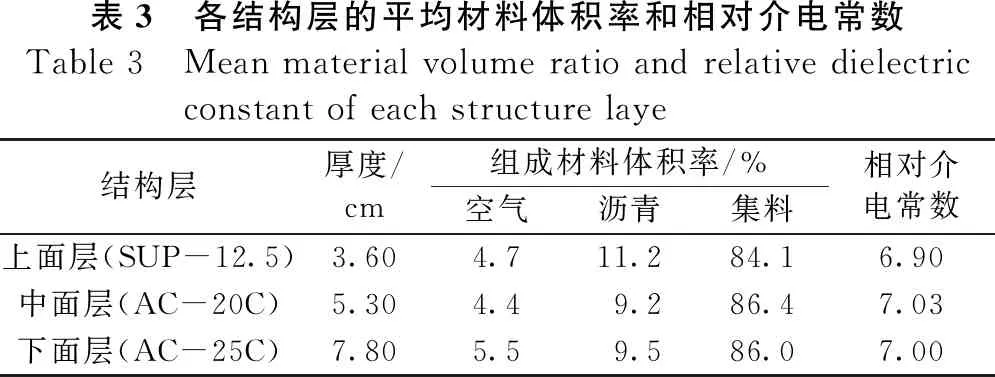
表3 各结构层的平均材料体积率和相对介电常数Table 3 Mean material volume ratio and relative dielectric constant of each structure laye结构层厚度/cm组成材料体积率/%空气沥青集料相对介电常数上面层(SUP-12.5)3.604.711.284.16.90中面层(AC-20C)5.304.49.286.47.03下面层(AC-25C)7.805.59.586.07.00

由分析可知：上面层的厚度为3.60 cm，相对介电常数平均值为6.90；下面层的厚度为5.30 cm，相对介电常数平均值为7.03，下面层的厚度为7.80 cm，相对介电常数平均值为7.00。

3 基于GPR正演技术的道路空洞含水率计算

3.1 网格划分

根据前文各结构层厚度、相对介电常数的结果，构建真实道路三维模型，并将模型导入程序中计算含水率与雷达反射波形的数学关系。由于沥青混合料试件由沥青和集料拌和而成，因此将模型中的每一层的沥青混合料视为定值。所建立的道路三维模型是一个10 m×0.22 m×1 m的长方体，如图5所示。上部为空气层，厚度为3.30 cm，相对介电常数为1.00；第1层介质为上面层，厚度为3.60 cm，相对介电常数为6.90；第2介质为中面层，厚度为5.30 cm，相对介电常数7.03；第3层介质为下面层，厚度为7.80 cm，相对介电常数为7.00。整个区域用单元1 cm×0.1 cm×1 cm的矩形单元进行单元划分，共划分为1 000×220×100的网格空间。

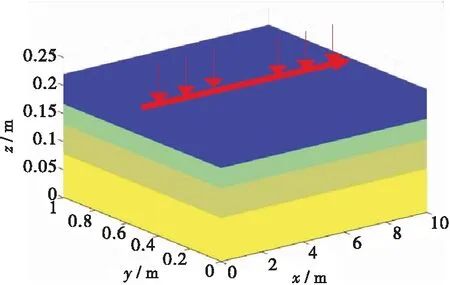
图5 真实道路三维模型

3.2 构建模型

将上述真实路面三维模型导入MATLAB计算程序中，将数值结果图像化处理，可得到单道反射波形图，如图6所示。

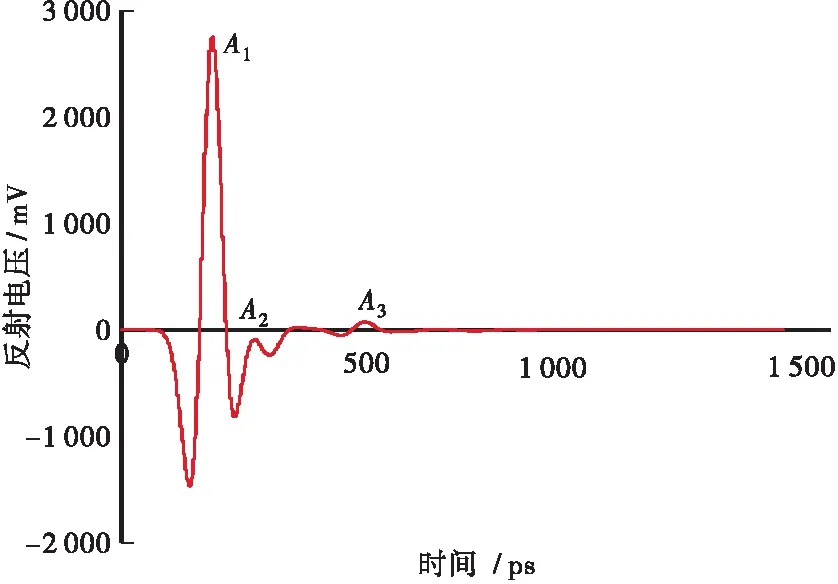
图6 单道反射波形图

图中A1为空气层与上面层产生的反射波幅；A2为上面层与中面层交界处产生的反射波幅；A3为中面层与下面层交界处产生的反射波幅。

由于雨水会从路表渗入和道路基层的水气会向上扩散，会导致在空洞处存在积水现象，且不易消除。由于水与空气的相对介电常数有这较大的差异，导致雷达在发射高频电磁波时会在两者接触面发生反射与折射现象[13]。因此，本文建立了不同含水率的三维空洞模型，来确定典型含水空洞雷达检测特征图像和单道反射波形图，从而得到含水率与反射波幅间的模型。

3.3 不同含水率空洞病害正演模拟

通过查阅历年工程养护情况和相关文献，可以得到汉十高速公路孝襄段的空洞病害一般出现在层间交界处，其中下面层的空洞病害最严重。因此本文为了提高空洞识别能力，假设空洞形状为5 cm×5 cm×2 cm的长方体空洞，且位于道路三维模型的中面层与下面层的交界处，其中心点空间坐标为(5 m，0.5 m，0.078 m)。同时选取了10%、20%、35%、50%、75%、100%的6种不同的含水率来建立三维空洞模型，如图7所示。

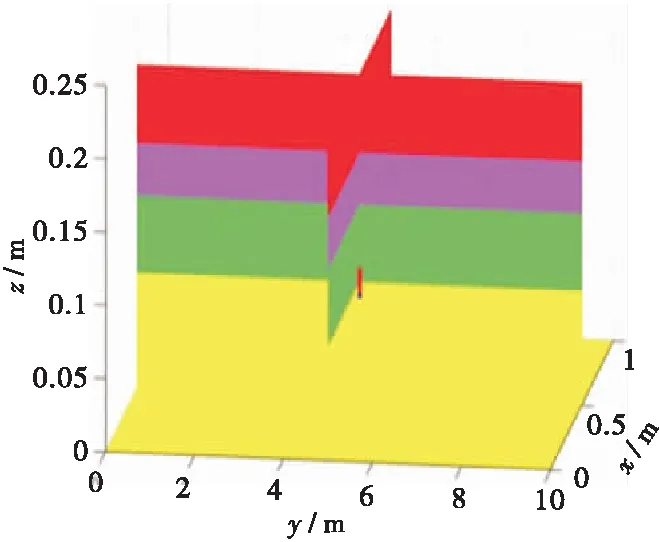
(a)10%含水空洞

将模型导入到MATLAB中，并将模拟结果进行图像处理，可得到电磁波在空洞正上方发射、接收所得的中心单声道反射波形图，由于该模型反射波峰较多，但在400 ps至450 ps内仅存在1个反射波峰，因此提取400 ps至450 ps间反射波谷进行绘图，如图8所示。将反射波谷的峰值与含水率进行线性拟合，如图9所示。

图8 反射波谷变化图

图9 空洞含水率与反射波谷拟合

根据含水率和该处的峰值可建立如下关系，即X表示含水率，Y表示该处峰值，单位为V，拟合公式为式(7)，相应R2=0.992 2。该式可以反映反射波谷峰值随空洞含水率变化的数学关系，可通过峰值反算空洞含水率的大小。

y=176.83x-121.6

(10)

3.4 实际应用

根据现有的研究表明，存在含水空洞的雷达检测二维剖面图容易在中下面层反射界面出现“红+蓝+红”特征图像，蓝色部分代表空洞中水的位置，红色部分代表空洞中上部的空气，通过“红+蓝”的位置准确定位空洞位置，与此同时随着这空洞含水率的增加，下部分红色线条将不断远离中下面层反射界面[14]。含水空洞病害的典型雷达检测二维剖面图见图10。

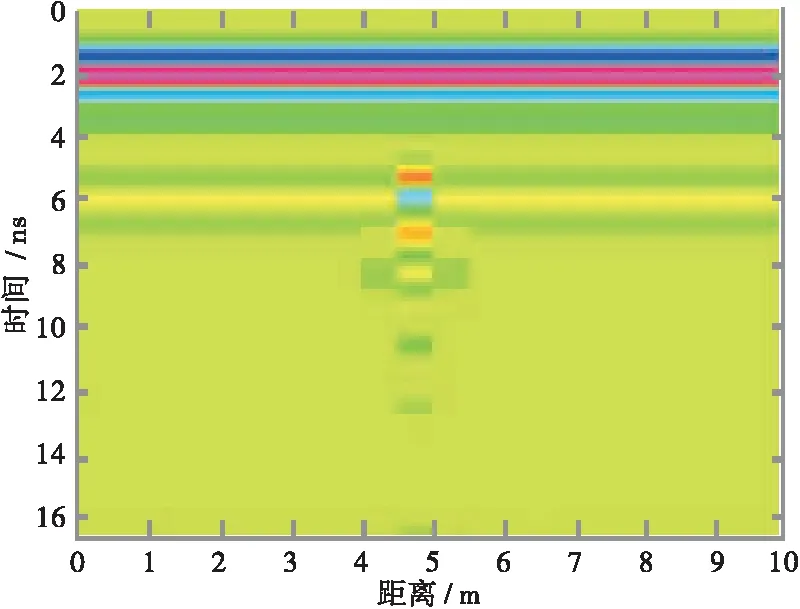
图10 含水空洞病害的典型雷达检测二维剖面图

基于这个典型特征，通过对照汉十高速公路实际雷达检测二维剖面图，发现汉十高速公路路面存在较多的含水空洞典型病害。图11、图12分别为汉十高速公路孝襄段实际含水空洞病害的雷达检测二维剖面图和反射波形图。

图11 实际雷达检测二维剖面图

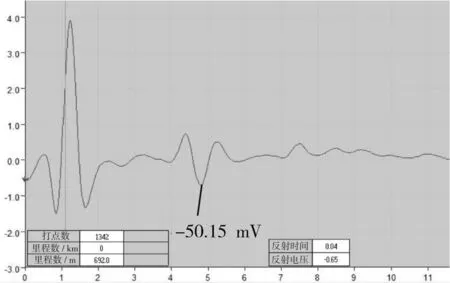
图12 雷达检测反射波形图

通过反射波形图可以得到反射波谷峰值为-50.15 mV，代入之前所得到的反射波谷峰值与含水率的计算模型中，可以得到该处的含水空洞的含水率为：40.41%，其余含水空洞病害的图像所在位置和含水率的大小如表4所示。

从表4可知，汉十高速公路孝襄段含水空洞病害共有6处，病害程度中等，特别是在K1156～K1158路段，如图13所示。该路段可能出现连续病害，养护部门应重点关注，及时养护，减少对路面造成的损伤。

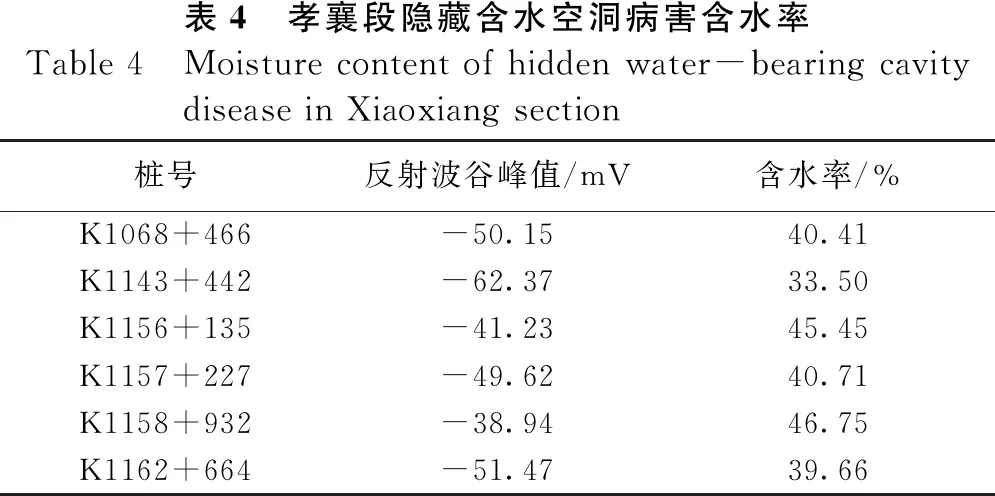
表4 孝襄段隐藏含水空洞病害含水率Table 4 Moisture content of hidden water-bearing cavity disease in Xiaoxiang section桩号反射波谷峰值/mV含水率/%K1068+466-50.1540.41K1143+442-62.3733.50K1156+135-41.2345.45K1157+227-49.6240.71K1158+932-38.9446.75K1162+664-51.4739.66

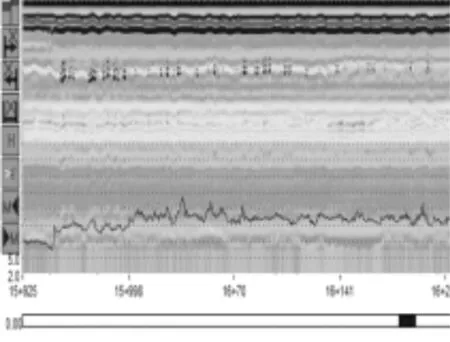
(a) 雷达二维剖面图

4 结语

本文通过对典型路面含水空洞模型的雷达正演模拟，得到典型含水空洞病害的雷达检测反射波形图，探究路面空洞病害含水率与反射波谷峰值之间的数学关联。主要结论如下：

a.本文通过推导求解电磁场的Maxwell方程组，并设置激励源和边界条件，得到GPR三维波动方程。基于该方程进行编写MATLAB代码，并将路面结构层厚度和混合料的相对介电常数导入，得到了真实道路三维模型。本正演模型是基于汉十高速公路实际路面数据建立的，但本文所提供的模型构建方法仍适用于其他高速公路，推动了探地雷达无损检测技术在道路结构病害的精细化检测的应用，为道路无损检测技术的未来发展奠定了基础。

b.本文发现在道路中下面层层间黏结处易含水空洞，因此在此处插入含水空洞模型，通过分析不同含水率的汉十空洞模型对电磁波在路面结构传播的影响，发现路面含水空洞含水率与反射波谷峰值呈线性关系，具体关系如式(10)所示，此数学关系式可以应用于汉十高速公路路面空洞病害含水率的计算。这对其他高速公路准确测量路面空洞含水率提供了参考依据，为路面雷达回波的正演模拟提供了一个有效的方法，也为进一步开展路面雷达电磁波反演打下了理论基础，具有极大的工程实际价值。