四维Minkowski空间中伪零曲线的结构函数

胡 娜，张亭亭，姜 杨

(1.沈阳工业大学 理学院，沈阳 110870；2.沈阳师范大学 数学与系统科学学院，沈阳 110034)

设R4为四维实向量空间,x=(x1,x2,x3,x4),y=(y1,y2,y3,y4),z=(z1,z2,z3,z4)为R4中的向量.在R4上定义内积为

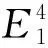
e1=(1,0,0,0),e2=(0,1,0,0),e3=(0,0,1,0),e4=(0,0,0,1).

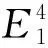
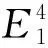
1 预备知识

(1)

其中T(s),N(s),B1(s),B2(s)分别是α(s)的切向量、主法向量、第一副法向量、第二副法向量,k1,k2称为伪零曲线α(s)曲率函数,且满足

〈T,T〉=〈N,B2〉=〈B1,B1〉=1,

〈B2,B2〉=〈N,B1〉=〈B1,B2〉=0,〈T,N〉=〈T,B1〉=〈T,B2〉=〈N,N〉=0.

2 主要结论

2.1 伪零曲线的表达形式

设伪零曲线α(s)的主法向量为α″(s)=(ξ1,ξ2,ξ3,ξ4)，因为α″(s)是类光向量,则

可得

(2)

于是伪零曲线的切向量与主法向量可表示为

N=α″=ρ(2f,2g,1-f2-g2,1+f2+g2).

注1若ξ3=±ξ4=f(s),则ξ1=ξ2=0,α″=(0,0,f(s),±f(s)).此时,α‴是类光向量,所以ξ3≠±ξ4.

定义1上述函数f(s)和g(s)称为伪零曲线α(s)的结构函数.

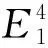
(3)

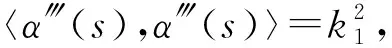
α‴=ρs(2f,2g,1-f2-g2,1+f2+g2)+2ρ(fs,gs,-ffs-ggs,ffs+ggs),

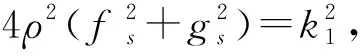
设B2=aα′+bα″+cα‴+dα(4),经计算可得

α(4)=ρss(2f,2g,1-f2-g2,1+f2+g2)+4ρs(fs,gs,-ffs-ggs,ffs+ggs)+

由〈B2,α′〉=〈B2,α‴〉=0,〈B2,α″〉=1和〈B2,B2〉=0,可得

B2=bα″+cα‴+dα(4),

(4)

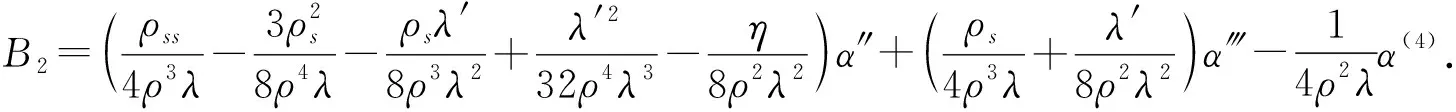
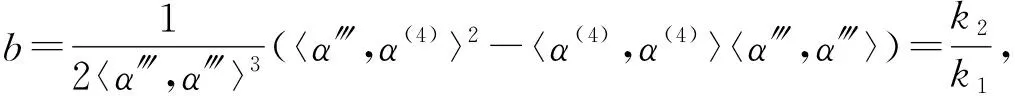
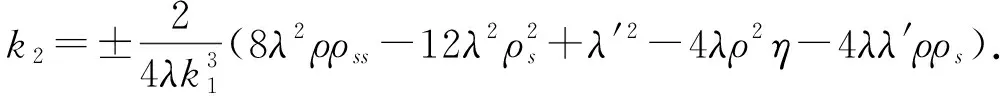
证毕.

(5)

则可得如下定理.

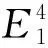
N=ρ(2f,2g,1-f2-g2,1+f2+g2),

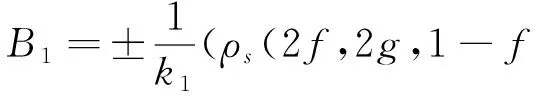
其中ρ满足式(5).

2.2 特殊曲率的伪零曲线

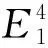
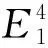
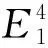
3 结语

本文讨论了四维Minkowski空间中的伪零曲线.通过建立伪零曲线的基本理论,提出结构函数的概念,从而得到曲率函数与结构函数之间的关系,同时利用结构函数给出伪零曲线的Frenet标架及曲线的表达形式.与之前对于此类曲线的研究相比,这种表达更加形象具体,为今后伪零曲线的进一步发展奠定了基础.