3中一类Kirchhoff方程的高能量径向解的存在性
杨金富,张家锋
(贵州民族大学 数据科学与信息工程学院,贵阳 550025)
研究如下形式的Kirchhoff方程高能量径向解的存在性问题:
(1)
其中a>0,b>0,4.5 (2) 该方程是由Kirchhoff在1883年的文献[1]中提出的,用来刻画弹性弦在横向振动过程中弦长变化的动态模型,其中0 (3) (4) 其中a,b,μ>0;对于方程(3)的研究结果,可参考文献[2-5],在这些文献中,当f满足线性、非线性或者奇异增长性时,作者得到了该方程解的存在性和多重性结果,而方程(4)的相关结果,感兴趣的读者可查阅文献[6-8];然而对于方程(2),在文献[3,6-7]中,可以看到,不同的作者通过变分方法、Nehari流形方法、极小极大方法得出了该类方程正解的存在性、唯一性以及多重性结果.但该类方程关于高能量解的文章非常少,因此,在某些自治非线性项的作用下,该类Kirchhoff方程是否会存在高能量解?下面将会回答这个问题. 在本文中,将使用下面这些记号. 1)H1(3)={u∈L2(3):∇u∈L2(3)}表示通常使用的Sobolev空间. 7)C1(H1(3),)表示H1(3)→上具有一阶连续导数(弱导数)的泛函所构成的空间. 8)c,ci,C,Ci为不同的正常数. 为了回答提出的问题,考虑含有纯幂次非线性项f(u)=|u|p-1u(4.5 (5) 显然I∈C1(H1(3),),且I关于∀v∈Hr1(3)的弱导数为 (6) (7) 引理1(i) ∃r>0,ρ>0,使得 (ii) 给定∀n∈,存在奇连续映射 使得,对于∀δ∈Sn,有 J(τ0n(δ))≤I(τ0n(δ))<0. (ii) 根据文献[11]的定理10,能发现∀n∈,存在一个奇连续映射3),使得∀δ∈Sn有ζn(δ)≠0;设B={x∈3|ζn(δ)≠0},由问题(5)结合4.5 根据文献[12]第9章,定义对称山路值如下 (8) 这里En={δ=(δ1,δ2,…,δn)∈n:|δ|≤1}并且定义映射集 属于Γn且∀n∈,Γn≠φ. 引理2设J(u)是由前面给出的,bn与(8)中的相同,则 (i)J(u)满足Palais-Smale条件;(ii)bn是J(u)的临界值;(iii) 当n→∞时,bn→∞. J(un)→C,J′(un)→0. (9) (10) 由 由式(9)易知 〈J′(un)-J′(u),un-u〉→0. 又由Hölder不等式和式(10)知 (ii) 由(i)知J(u)满足Palais-Smale条件,根据参考文献[12]中的定理2.2,易知J(u)存在临界值bn,即(ii)成立. 这里i(Y)表示集合Y的亏格,εm是∈3{0}的闭集族,使得-A=A且i(A)是集合A的Krasonelski亏格.由文献[13],定义另一个极小极大值序列 则∀n∈,有bn≥dn且d1≤d2≤…≤dn≤dn+1≤…;此外,由于J(u)满足Palais-Smale条件,则稍微修改文献[14]第9章中的参数,便得到dn→∞(n→∞),则bn→∞(n→∞). I(uj)→an>0,I′(uj)→0. (11) 由式(5)和式(6)得 (12) 又由式(6)和式(11)知 (13) 由式(6)知 将两式相减得 由式(11)易知,〈I′(uj)-I′(u0),uj-u0〉→0(j→∞);又根据式(12)和Hölder不等式知 I(u0)=an,I′(u0)=0. 从文献[2-7,9-10]可以看到,一些Kirchhoff方程解的存在性、多重性、唯一性等主要结果已经通过不同研究者的努力展现在眼前,而本文则通过研究得到了一类Kirchhoff方程高能量解的存在性.因此,本文可作为文献[2-7,9-10]中相关结果的一种补充.

1 预备知识

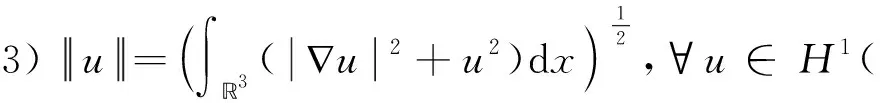



2 主要结果与证明


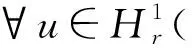

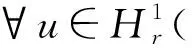
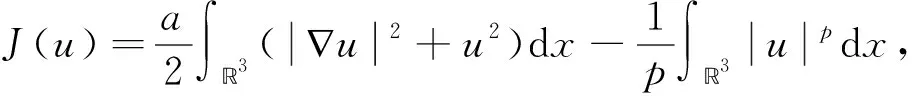
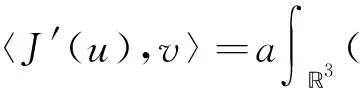
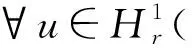


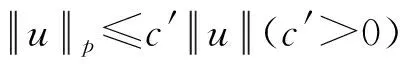
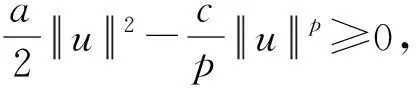
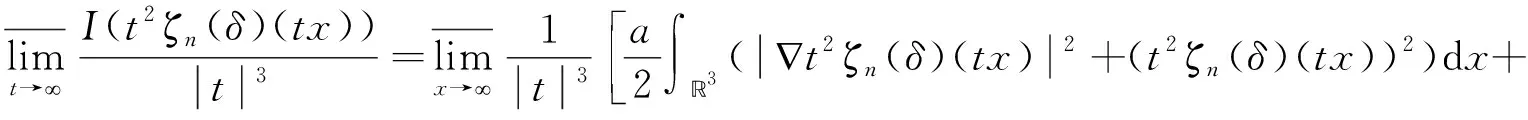
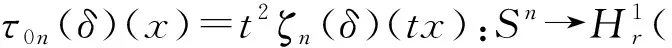
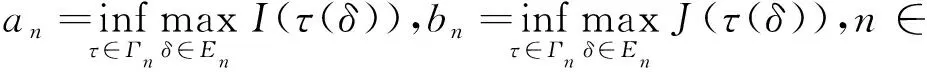


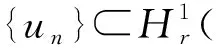




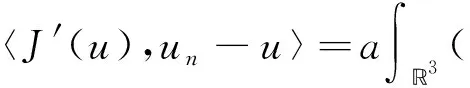
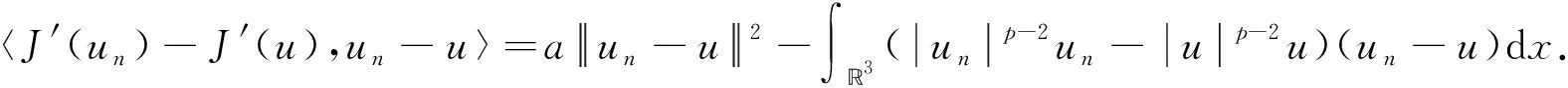
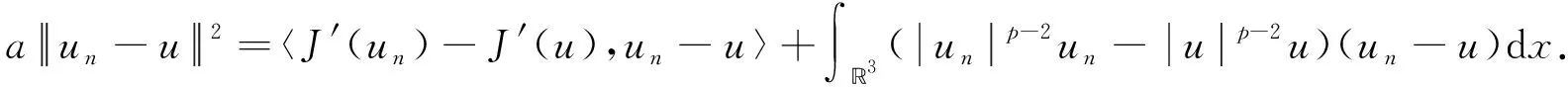

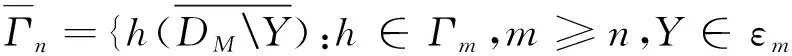






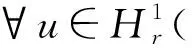
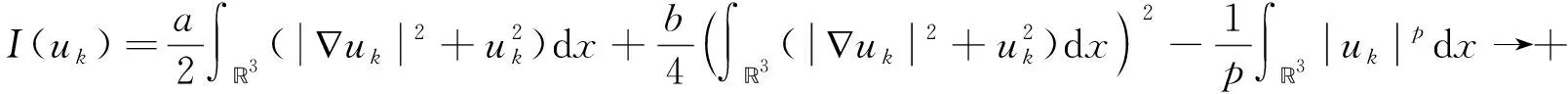
3 结语

