交换折叠超立方体的2-外连通度①
蔡学鹏, 刘梦瑶, 杜濛雨
新疆农业大学 数理学院, 乌鲁木齐 830052
在本文中, 术语图和网络可以互换使用. 所有的图都认为是无向的简单连通图, 对于未说明的图论符号和术语, 可参见文献[1-3].
设G=(V(G),E(G))是一个图. 对于图G中的任意顶点u∈V(G), 设集合{v∈V(G){u}: (u,v)∈E(G)}和集合{(u,v)∈E(G):v∈V(G){u}}分别表示顶点u的邻点集和邻边集, 记作NG(u)和NEG(u).dG(u)=|NG(u)|称为图G中顶点u的度. 对于图G的子图K, 设
分别表示子图K在G中的邻点集和邻边集.
图G的经典连通度κ(G)和边连通度λ(G)是衡量网络可靠性和容错性的两个重要参数[4-5]. 连通度κ(G)和边连通度λ(G)越大, 网络的可靠性就越高. 但是, 这两个参数有明显的不足之处, 比如, 在互连网络的实际应用当中, 与一个处理器相连接的所有处理器(链路)同时发生故障的可能性较低, 所以用这两个参数衡量网络可靠性和容错性是不精确的. 为克服这些不足之处, 可以通过对G-S的每一个分支强加一些限制条件来推广图G的经典连通度(边连通度), 这里S⊂V(G)(S⊂E(G)). 文献[6]首次考虑了这个问题并且提出了图G的条件连通度(边连通度)的概念.
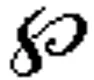
设S⊂V(G)(S⊂E(G))且g是非负整数, 如果G-S是不连通的, 且G-S的每个连通分支中至少有g+1个顶点, 则称S是G的一个Rg-割(Rg-边割). 若G存在Rg-割(Rg-边割), 则G的所有Rg-割(Rg-边割)中基数最小的Rg-割(Rg-边割)的基数称为G的g-外连通度(g-外边连通度), 记为κg(G)(λg(G)). 明显地, 如果G不是完全图, 则κ0(G)=κ(G)且λ0(G)=λ(G). 因此,g-外连通度(g-外边连通度)可以认为是经典连通度(边连通度)的一种推广形式, 并且能更加精确地衡量大型并行处理系统的可靠性和容错性. 网络(图)的g-外连通度(g-外边连通度)已被许多学者研究, 详细结果可参见文献[6-16]及相关文献.
在平行计算系统中,n维超立方体Qn[17]、n维折叠超立方体FQn[16]和交叉超立方体EH(s,t)[18]是3个重要的互连网络. 基于这3个网络, 文献[19]提出了一个新的网络交换折叠超立方体EFH(s,t),EFH(s,t)是在EH(s,t)的基础上增加了一些边获得的, 并且这些边称为补边. 交换折叠超立方体有许多重要的特性, 比如它有短的直径和低消费因子.
文献[20-21]探究了交换折叠超立方体EFH(s,t)的连通度和边连通度, 并且证明了
κ(EFH(s,t))=λ(EFH(s,t))=s+2 1≤s≤t
文献[22]证明了
λ2(EFH(s,t))=3s+2 6≤s≤t
本文将探讨交换折叠超立方体EFH(s,t)的2-外连通度, 最终确定了
κ2(EFH(s,t))=3s+2 5≤s≤t
1 预备知识
一个n元二进制字符串x=xn-1xn-2…x0的第i个字符记为x[i], 0≤i≤n-1.
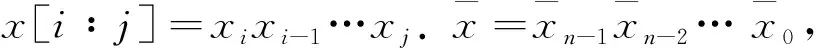
定义1[19]设交换超立方体EH(s,t)=G(V,E),s,t是正整数. 交换超立方体的点集V(EH(s,t))={as-1as-2…a1a0bt-1bt-2…b1b0c:ai,bj,c∈{0, 1}, 0≤i≤s-1, 0≤j≤t-1}, 交换超立方体的边集E(EH(s,t))={(u,v): (u,v)∈V(EH(s,t))×V(EH(s,t))}由3种类型的边E1,E2,E3构成. 其中
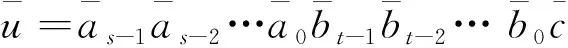

图1 EH(1, 2)和EFH(1, 2)
设u∈V(EFH(s,t)). 通过定义2, 如果u[0]=0, 则d(u)=s+2, 否则d(u)=t+2.
下面给出EH(s,t)和EFH(s,t)的一些结论, 主要结果的证明将会用到这些结论.
引理1[4]κ(EH(s,t))=λ(EH(s,t))=s+1, 1≤s≤t.
引理2[10]κ1(EH(s,t))=λ1(EH(s,t))=2s, 1≤s≤t.
引理3[10]EH(s,t)同构于EH(t,s).
引理4[23]EFH(s,t)同构于EFH(t,s).
通过引理3和引理4, 可以在下面讨论中设s≤t, 则δ(EH(s,t))=s+1且δ(EFH(s,t))=s+2.
引理5[10]EH(s,t)可分解成两个EH(s-1,t)或两个EH(s,t-1).
根据EFH(s,t)的定义容易得出EFH(s,t)具有下面性质:
性质1交换折叠超立方体网络EFH(s,t)可以分解成两个子图L和R, 其中
V(L)={0as-2…a0bt-1…b0c:ai,bj,c∈{0, 1}, 0≤i≤s-2, 1≤j≤t-1}
V(R)={1as-2…a0bt-1…b0c:ai,bj,c∈{0, 1}, 0≤i≤s-2, 1≤j≤t-1}
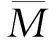
文献[14]证明了折叠超立方体FQn(n≥4)中不含3圈, 并且任何不相邻的两个点的共同邻点的个数不超过2. 因此容易得到下面的引理:
引理6交换折叠超立方体EFH(s,t)中不含3圈, 并且任何不相邻的两个点的共同邻点的个数不超过2.
引理7若P为EFH(s,t)中任意一条长度是2的路, 则|NEFH(s, t)(P)|≥3s+1.
证由EFH(s,t)的定义及引理7, 容易证明|NEFH(s, t)(P)|≥3s+1.
引理8[10]设K⊂V(EH(s,t))并且|K|<2s,s≥2. 则EH(s,t)-K满足下面两种情形之一:
(i)EH(s,t)-K是连通的;
(ii)EH(s,t)-K有两个分支, 其中一个分支是一个孤立点.
2 交换折叠超立方体网络的2-外连通度
定理1设EFH(s,t)=L⊕R, 对于任意的F⊆V(EFH(s,t)). 令FL=F∩V(L),FR=F∩V(R). 如果|F|≤3s并且EFH(s,t)-F中既无孤立点也无孤立边, 则R-FR(或L-FL)中每一个顶点均与L-FL(或R-FR)中的一个顶点连通.
证对于任意的顶点u=1as-2…a0bt-1…b0c∈V(R-FR), 分以下两种情形进行讨论:
情形1u=1as-2…a0bt-1…b00.
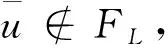
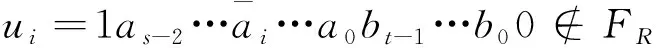
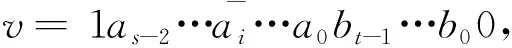

因为EFH(s,t)-F中不存在孤立边, 我们令
使得(v,w)∈E(R). 可以构造连接w至L-FL的点不交路径, 即路径如下:
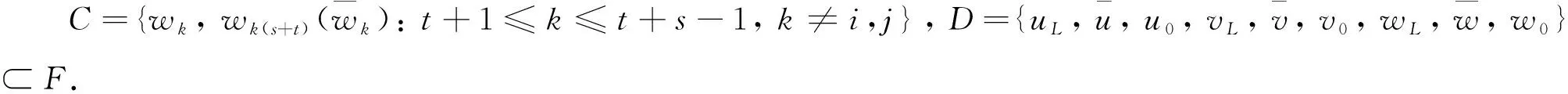
|F-(A∪B∪D)|=|F|-|A|-|B|-|D|≤3s-(s-1)-(s-2)-9=s-6
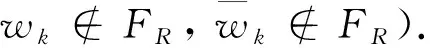
情形2u=1as-2…a0bt-1…b01.
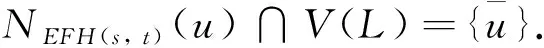

若|B′| 其中1≤k′≤t且k′≠i′,j′. |F-(A′∪B′∪C′)|≤3s-t-(t-1)-4≤s-3 而u通过w可构造t-1条路径, 因此至少存在1条路径使得u与L-FL中的一个顶点相连接, 定理1得证. 定理2k2(EFH(s,t))=3s+1, 其中s≥5. 证设P为EFH(s,t)中一条长度为2的路径, 由引理7可知|NEFH(s, t)(P)|≥3s+1. 通过EFH(s,t)的定义,EFH(s,t)-(NEFH(s, t)(P)∪V(P))既不包含孤立顶点也不包含孤立边, 因此NEFH(s, t)(P)是EFH(s,t)的一个R2-外割, 进一步可知k2(EFH(s,t))≤3s+1. 接下来只需证明k2(EFH(s,t))≥3s+1, 即证明对于任意的顶点集F⊆V(EFH(s,t)), 当|F|=3s且不存在孤立顶点也不存在孤立边时,EFH(s,t)-F是连通的. 设EFH(s,t)=L⊕R. 方便起见, 我们设 FL=F∩V(L)FR=F∩V(R) 情形1L-FL是连通的. 由定理1, 可知R-FR中任意一顶点与L-FL中一顶点连通. 因此EFH(s,t)-F是连通的. 情形2L-FL有两个连通分支, 其中一个是孤立点. 设u=0as-2…a0bt-1…b0c是L-FL中的一个孤立点, 此时有|FL|≥|NL(u)|≥s. 接下来证明EFH(s,t)-F中的u与L-FL-{u}是连通的. 考虑下面两种情形: 由于 |F-(NL(u)∪A∪{v0,vs+t})|≤3s-s-(s-1)-1=s 且u通过vi可构造s+1条通向L-{u}的路径, 故至少存在一条路径使得u与L-FL-{u}连通, 定理2得证. 由于 且u通过v(或w)可构造s+t(≥2s)条通向L-{u}的路径, 故至少存在一条路径使得u与L-FL-{u}连通, 定理2得证. 所以F中至多有2s-3个点在D中. 因此在D中至少存在一对点不属于F. 即u与L-FL-{u}连通. 本文在交换折叠超立方体网络经典连通度和超连通度的基础上深入研究, 进一步研究了其2-外连通度, 证明了: 当t≥s≥5时,k2(EFH(s,t))=3s+1. 也就是说,EFH(s,t)中至少删除3s+1个顶点, 才能得到不包含孤立顶点和孤立边的非连通图.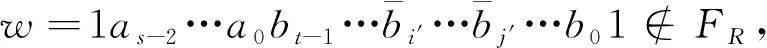
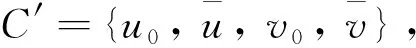


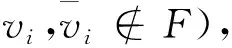

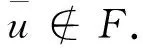
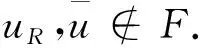
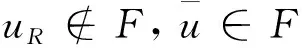
3 小结

