基于深度学习的高精度交通流量大数据预测①
周思吉, 钱真坤
1.四川文理学院 信息化建设与服务中心, 四川 达州 635000; 2.四川文理学院 后勤服务处, 四川 达州 635000
大数据时代下的智慧城市, 交通数据增长迅速, 给交通管理带来很大压力, 将传感技术、 图像、 控制技术等集成运用到管理系统的智能交通系统(Intelligent Transportation System, ITS)应运而生[1-2]. 交通预测对于ITS、 交通管理部门和旅行者来说必不可少, 采用最先进的机器学习算法对大流量数据集进行研究, 设计可靠的驾驶员支持系统, 可以避免致命事故的发生[3-4]. 在交通监控等实时应用中, 需要处理大量的数据, 由于不同位置的非线性时间动态特性、 复杂的空间相关性和更广泛的步长预测, 使交通预测成为一项具有挑战性的任务. 为了适应这些情况, 需要高效的可视化和数据挖掘技术来预测和分析海量的交通大数据[5-6].
文献[7]提出一种用于处理大传感器数据的收敛模型, 该模型包括使用雾、 云和移动计算技术的3层, 在收敛模型框架内实现了用于数据处理的多主体方法. 文献[8]提出基于大数据技术的软件定义网络(Software Defined Network, SDN)流量监控方法, 该方法使用计数器来收集和生成流量统计信息. 近几年来, 深度学习吸引了许多研究者将其应用到交通相关领域, 为了有利于道路信息的获取, 利用深度学习算法对交通流模式进行分层设计, 提取有用信息. 文献[9]提出一种长期短期记忆深度模型的交通预测方法, 能够提取精确的潜在空间相关性, 提高预测精度. 文献[10]提出一种改进的深度置信网络流量预测方法.
提高预测精度是交通流量预测需要解决的关键问题, 为了最大限度地提高预测精度和可扩展性, 目前已有许多相关研究[11]. 文献[12]提出一种利用大数据、 内存计算、 深度学习和图形处理单元(Graphics Processing Units, GPU)进行智能流量预测算法, 对大规模、 快速、 实时的交通进行预测. 文献[13]提出一种用于城市快速道路交通状态分类的机器学习方法, 该方法采用改进的模糊C均值(Fuzzy C-Means, FCM)聚类算法对城市交通状态进行分类. 但该算法仅适用于城市高速公路的交通状态分类, 未考虑交通碰撞对城市道路交通状态产生的影响. 文献[14]提出一种基于机器学习的城市交通事故安全黑点识别算法, 该算法采用基于最大分类区间的支持向量机对研究区域内的复杂模型进行训练和事故黑点优化学习, 并基于深层神经网络来识别和分析交通事故黑点. 由于交通事故数据特征随时间和空间的变化而变化, 难以确定造成黑点的原因, 黑点识别模型的训练将变得非常复杂.
为了进行不同位置的非线性时间动态特性、 复杂的空间相关性和更广泛的步长预测, 本文提出一种高精度基于深度学习的并行卷积神经网络(Convolutional Neural Networks, CNN)的流量大数据预测模型, 通过检测目标的存在性和其感兴趣区域(Region Of Interest, ROI)的几何属性(位置和方向)来预测特定区域的交通状况. 在该模型中保留交通信息, 并基于已有知识开发可视化, 通过不断变化的交通状况动画设计, 在特定的道路和时间可以分析收费公路的交通行为, 通过将预测结果与实际交通数据进行比较, 评价该方法的有效性. 实验结果表明, 本文提出的模型在准确度方面优于所对比的方法.
1 基于深度学习的交通大数据预测
本文提出的模型首先对数据进行收集和预处理以获取有效的输入数据集, 然后构造和训练并行CNN模型, 最后对交通流量特征进行预测. 本文提出的系统模型如图1所示.
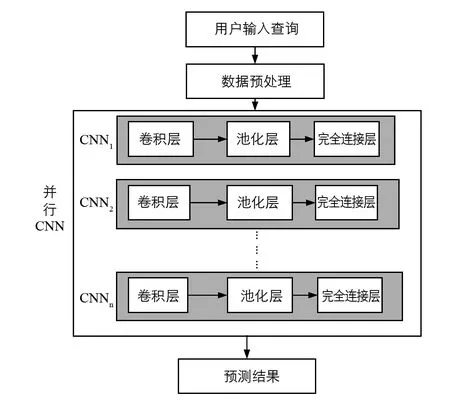
图1 本文提出的系统模型
1.1 并行卷积神经网络
卷积神经网络(CNN)是在传统神经网络的基础上发展起来的, 它作为图像识别、 语音识别和计算机视觉的一部分, 避免了对图像的复杂前期预处理, 在许多领域得到了广泛的应用. CNN的核心思想是通过局域感受卷积、 权共享和下采样对神经网络结构进行优化, 减少神经元个数和权值, 采用池化技术使特征具有位移、 缩放和扭曲不变性.
并行卷积神经网络是N级并行卷积层的独立卷积网络, 其中每级卷积网络设计为5层结构: 输入层、 卷积层、 池化层、 完全连接层、 输出层. 并行CNN能够提取更多维度和有代表性的特征, 具有较强的流量识别能力. 本文将具有规则时间间隔的一维时间序列样本和图像视为时间一维、 位置一维的二维像素网格, CNN中的卷积核可以有效地提取数据中的特征, 使得CNN在处理网格结构的数据时非常强大. 池化层的引入不仅大大减少了模型训练过程中的参数数目, 而且保证了通过卷积层提取的特征得到有效保留. 基于CNN的流量预测框架如图2所示.
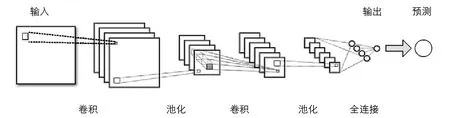
图2 基于CNN的流量预测框架
1.2 数据预处理
如何将流量数据组织起来作为深度学习网络的有效输入是一个重要的问题. 为了获得高质量的学习和预测结果, 需要对交通数据进行有效的组织, 形成有效的输入数据集. 输入数据必须适合深度学习网络的学习和预测, 并有效且有意义地代表正在研究的问题. 本文将交通数据转换为矩阵形式进行处理, 使用时空交通流矩阵作为CNN的输入进行回归预测. 根据时间和空间维度, 将不同位置采集的线圈数据视为时间一维、 位置一维的二维像素网格.
(1)
其中,Q为时间长度,P为空间长度. 构造的交通数据矩阵作为CNN模型的输入数据, 预测路段的预测交通流量作为其输出.
1.3 卷积层
卷积层是CNN特有的最重要的计算层, 卷积层的计算过程由卷积核的卷积运算完成. 卷积的函数设计为使用加权函数w和扫描函数x. 连续卷积运算定义为:
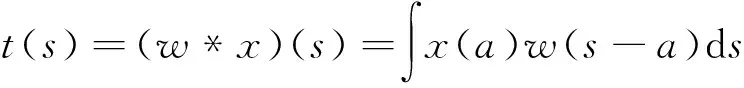
(2)
在机器学习应用中, 输入数据是离散的、 多维的. 以二维图像为例, 可以将二维离散变换定义为:

(3)
其中,j和k为二维图像坐标,I(p,q)表示输入矩阵,K(p,q)称为内核或特征映射. 如图2所示, 卷积运算使用特征映射来扫描图像, 测量其相似度并输出热图t(j,k), 突出显示感兴趣的区域. 如果在没有监督的情况下从图像中提取特征图, 那么热图t(j,k)会指示人脸的位置(除非没有人脸).
1.4 池化层
池化层(也称为下采样)被视为是对社区响应的总结. 池化通过减少输出大小来删除未使用的信息, 从而减少计算成本并避免过拟合, 有助于使网络对输入的微小变化保持不变. 最大池化是最成功的池化操作之一, 它输出矩形邻域内的最大值. 实践中可以通过两种不同的池化机制来执行该操作: 最大或平均. 一维中最大和平均池化操作表示为:
(4)
(5)
其中,q表示滤波器大小,p是起始索引,nq是结束索引,ri是输出向量.
1.5 完全连接层
卷积层和池化层输出的数据包含输入数据最终和最重要的特征. 在进入完全连接层之前, 应将其转换为适合完全连接层处理的一维向量形式.
(6)
最后, 一维向量通过计算全连通层产生模型输出.
1.6 基于预测因子的交通预测
为了探索交通, 选择了3个不同的公路站进行交通分析. 每个连接点都记录了15~20 min之间的信息. 相关的信息集用来比较不同聚合类型每个站点的数据. 备用信息集用于汇总季节性信息, 例如小时、 日、 月和年. 假设此时的主要道路交通会受到道路状况的影响, 如维修、 事故、 交通堵塞和其他情况. 由于本文的研究涉及到探索卓越地理位置中道路的动态特性, 因此需要根据时间和位置考虑不同的交通条件. 并非所有道路同时处于相同的交通状态或处于类似的状况.
在时间(t+h), 用给定的测量值预测在时间t的交通流速度. 交通函数定义为:
(7)
为了对交通流数据进行建模, 应用以下公式得出预测因子x:
(8)
其中,n表示网络中的位置数(环路检测器),xi, t表示在时间t, 位置为i时横截面交通流速度,VT表示矩阵转换为列向量的向量化转换. 选定的长度一致, 并且与几个现有的运输走廊管理部署相对应. 这些层是用时间序列“过滤器”按如下方式计算的:
(9)
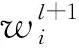
2 卷积神经网络的训练
采用VGG(Visual Graphics Generator)网络结果进行训练和测试, 在训练的开始阶段随机初始化参数. 训练过程分为前向传播计算和反向传播计算两个阶段. 前向传播按下式进行计算:
xi=ayi-1+b,yi=f(xi)
(10)
其中,xi为当前层输入,yi为当前层输出,a和b为上一层的权重和偏置,f(xi) 为激励函数. 采用具有快速计算和快速收敛特性的修正线性单元(Rectified linear unit,RELU)作为激励函数,RELU=max(0,y).
反向传播的核心是计算损失函数值, 本文采用平方误差函数作为损失函数, 表示为:
(11)
其中,N为样本数量,n为训练次数,z为训练样本的正确结果,o为网络训练的输出结果.
由于网络模型的参数过多, 在训练过程中存储的数据将影响训练和测试速度, 需要对参数进行优化. VGG网络的训练参数主要产生于完全连接层, 为了减少VGG网络的训练参数, 去掉一层完全连接层, 保留原VGG网络结构不变, 以减少训练参数.
3 实验结果与分析
为了在分布式环境中实现流量预测和可视化, 所有实验均在配置为Intel(R)Core(TM)i3-2350M CPU@2.30 GHz、 2300 MHz、 4 Core(s)的4个逻辑处理器(24 GB内存)上, 采用Matlab 2014a神经网络工具箱实现了本文提出算法的模型. 在训练早期使用均方误差来加速参数优化, 更快地拟合高峰时段的流量高值数据. 为了预测和可视化实例, 使用带有流量数据集的P-CNN分类器.
为了将交通数据进行预测和可视化, 本文从北京交通部门的分布式传感器中收集交通数据, 并将收集到的每个探测器站的数据以15 min间隔进行聚合. 为了验证结果, 首先使用2019年的半年数据, 将2019年1月1日至2019年4月30日的交通数据视为训练集, 2019年4月1日至2019年6月30日的交通数据视为验证集, 2019年5月1日至2019年6月30日的流量数据视为测试集. 在训练期间将模型应用于测试集之前, 首先将验证集用作防止过度拟合的指标, 然后备份训练. 为了验证该方法, 本文使用一些用于数据收集、 存储、 数据操作以及数据质量和性能因素的策略. 数据集中的特性包括起点、 终点、 时间戳、 可见性、 压力等级、 速度和区域. 生成的数据集随机用于培训、 测试和验证. 表1说明了包含特征数、 类别数和实例数的流量数据.

表1 数据集描述
3.1 评估指标
模型的精确度主要通过模型预测数据与真实数据之间的误差来反映, 为了评价本文提出模型的分类性能, 采用分类中常用的3种指标进行估计: 平均绝对误差(Mean Absolute Error,MAE)、 平均相对误差(Mean Relative Error,MRE)和均方根误差(Root Mean Square Error,RMSE).MAE能够更好地反映预测值误差的实际情况,MRE能够反映模型所得结果的绝对误差与预测值之间的百分比, 较好地体现了模型的可信度,RMSE用来衡量观测值同实际值间的偏差.
(12)
(13)
(14)
其中,qk是预测流量,pk为实时流量,m为测试数据的样本数量.
3.2 实验结果与分析
表2至表4给出了K-最邻(K Nearest Neighbor, KNN)、 带漂移检测的快速增量模型树(Fast Incremental Model Trees, FIMT)、 卷积神经网络(Convolutional Neural Network, CNN)和本文所提模型的MAE,MRE和RMSE.
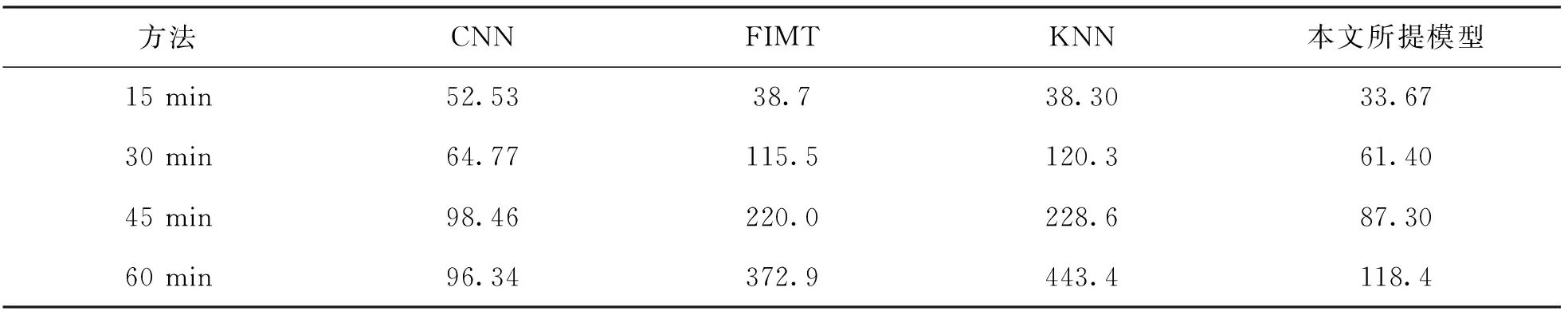
表2 不同模型的MAE性能指标
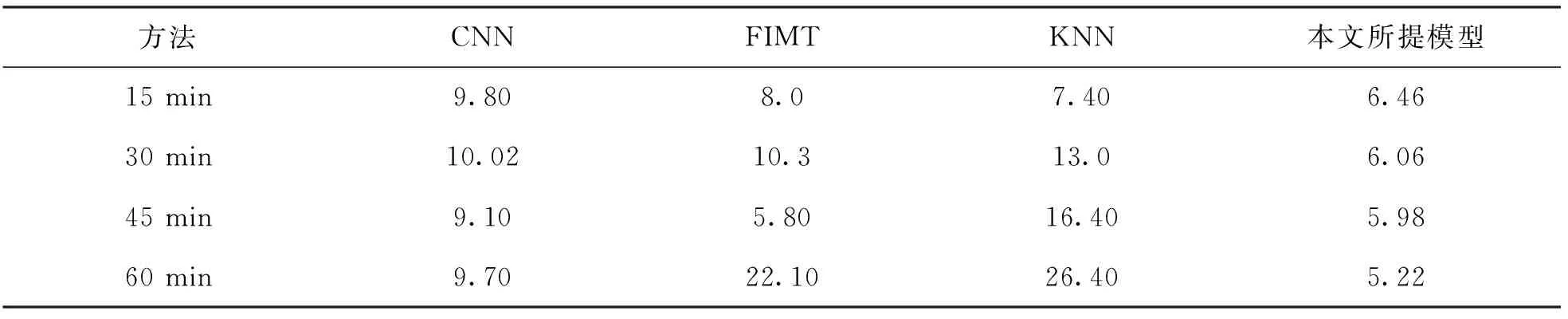
表3 不同模型的MRE性能指标
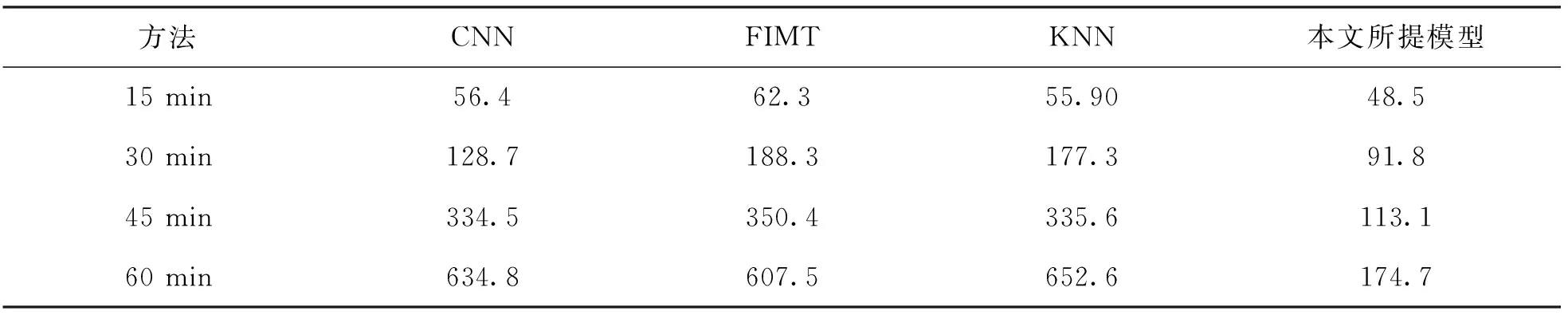
表4 不同模型的RMSE性能指标
由表2至表4可以看出, 在短期预测方面, 与KNN,FIMT,CNN相比, 本文所提模型在MAE,MRE和RMSE方面优于所对比的模型. 这是因为本文模型将具有规则时间间隔的一维时间序列样本和图像视为时间一维、 位置一维的二维像素网格, 通过学习这些特征来对某路段的交通流量进行预测, 可以有效地编码交通流量预测中的时间相关性, 在短期预测期间取得了较好的预测结果.
在使用不同性能指标计算平均错误率后, 使用不同模型对每日、 每周、 每月和每年高速公路数据进行预测的准确度如图3所示. 由图3可以看出, 在长期预测方面, 本文模型比其他现有模型具有更好的精度. 这是因为本文使用并行CNN对交通流量进行预测, 在预测过程中添加了检测目标的存在性和感兴趣区域的几何属性(位置和方向), 同时探索卓越地理位置中道路的动态特性, 根据时间和位置考虑不同的交通条件设置了预测因子, 并应用预测因子对交通流数据进行建模, 进一步提升了特定区域交通状况的预测精度.

图3 各模型的准确度
4 结论
本文提出一种高精度基于深度学习的并行卷积神经网络的交通流量大数据预测模型, 以高效数据挖掘技术来预测和分析海量交通大数据. 该模型首先对数据进行收集和预处理, 将交通流数据转化为二维图像来构建并行CNN, 通过学习这些特征来对某路段的交通流量进行预测. 引入预测因子对交通流数据进行建模并预测实验, 本文所提模型的流量数据预测性能均优于所对比的方法. 未来的工作是研究基于深度学习的交通信号灯长度优化, 探讨城市交通信号灯对交通的影响, 并使所有用户能够根据交通流量预测监测空气质量.

