中国经济转型时期的劳动生产率——影响因素和增长分解

邓金锋，杨 娟

(北京师范大学 经济与工商管理学院，北京 100875)

一、引言

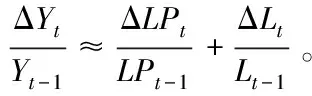
图1 1978—2019年中国GDP增速和劳动生产率增速数据来源:国家统计局，http://data.stats.gov.cn/easyquery.htm?cn=c01

2010年以后，中国经济发展进入转型期。在达到刘易斯拐点之后，中国劳动力供给开始下降，劳动力成本不断增加，中国经济发展进入“新常态”。在这一新阶段，产业结构表现主要为服务业占比超过第二产业，制造业由资本密集型产业向技术密集型转变。

在新阶段下，基于要素和投资驱动的经济增长已不可持续。就劳动力要素来看，中国面临劳动力成本不断上升、劳动力供给持续下降、人口老龄化加速和生育率较低的问题；从资本要素投入来看，迈过2010年后，中国第二产业和第三产业的固定资产投资完成额增速呈下降趋势，2011年，中国第二产业和第三产业固定资产投资完成额增速分别为27.3%和21.1%，之后处于增长减速阶段，到2019年，增速分别下降至3.2%和6.6%。

站在21世纪的第三个十年，中国经济发展面临的外部和内部环境更加复杂。一是2008年全球金融危机后，单边贸易保护主义抬头，且与民粹主义、“逆全球化”互相呼应。二是2020年爆发的新冠肺炎疫情对全球经济造成巨大冲击，后疫情时代各国经济恢复缓慢，疫情反复给各国财政和货币政策带来巨大挑战，世界经济发展充满了不确定性。三是“十四五”期间，中国发展面临的矛盾和问题集中在发展质量上，能否实现扩大内需、进一步优化经济结构、以创新促发展等目标将是中国经济实现高质量发展和2035远景规划目标的关键。

实现经济高质量、持续发展，意味着需要不断提高劳动生产率。2021年3月，政府工作报告提出“十四五”期间“全员劳动生产率增长高于国内生产总值增长”的目标。单从数学意义上理解，这一目标似乎很容易实现，毕竟中国从业人员数量处于持续下降状态，只需国民生产总值保持增长即可。但从实际意义来说，这一目标是要求国内生产总值应由劳动生产率的提高拉动，保持合理与健康的劳动生产率增速将决定中国的经济发展速度和质量。

深入分析影响中国劳动生产率增长的因素，有利于正确认识劳动生产率和经济增长，挖掘新时期经济增长的潜在动力。通过对新古典增长模型进行扩展，本文得到包含产业结构转变、资本深化和教育因素三方面的劳动生产率生产函数，并利用各省市1998—2019年数据进行OLS回归分析；进一步地，对不同阶段劳动生产率的增长进行RIF分解以探究不同因素的增长贡献。本文的意义在于：回归分析的结果肯定了中国经济在结构转型升级时期确实经历了“结构性减速”，但也认可产业结构转变的积极作用，即促进上侧分位数上的劳动生产率增长；同时，本文还发现教育数量和教育质量对劳动生产率产生影响时的相互影响。

二、相关文献回顾

在众多研究劳动生产率的文献中，可以按照影响劳动生产率的因素进行分类，这些因素包括：产业结构和全球产业链分工、资本深化、教育和人力资本、市场配置资源有效性、创新和技术进步、城市规模、环境等。本文主要关注产业结构、出口结构、资本深化、教育人力资本四方面与劳动生产率关系的研究成果。

1.产业结构和劳动生产率

把产业结构升级看作生产要素从低生产率部门向高生产率部门流动优化的过程，那么结构变化对经济增长具有正向作用；而“鲍莫尔成本病”观点认为，劳动力不断从进步部门转移到停滞部门，最终会导致整体生产率的降低。1990年以后，非洲和拉丁美洲国家的产业结构工业化转变处于下降态势，那些依赖于自然资源出口的国家，劳动力从高生产率部门流向低生产率部门，导致整体劳动生产率降低。有学者使用1973—1990年联合国工业开发组织39个国家和24个行业的数据对劳动生产率增长进行分解，发现尽管总体上产业结构服务化转变对劳动生产率有负向作用，但那些致力于发展电子行业的国家实现了劳动生产率更快的增长。还有学者对俄罗斯1995—2012年劳动生产率的增长进行了分解，发现结构变化的影响是随着劳动生产率增速增加、随时间降低的。罗宾森(Robinson)等对中国1978—1995年的经济增长进行实证分析，认为通过将要素资源从低生产率部门转移至高生产率部门，产业结构工业化对经济增长有正向影响；但是，李文兵等对1979—2005年中国的劳动生产率和全要素生产率增长进行了分解，认为三次产业结构转变期间没有产生明显的“结构红利”。对中国2010年后经济增长的相关研究认为，中国经济正在经历“结构性减速”。产业结构“服务化”对劳动生产率的负向影响被部分学者用于解释2011年以来中国经济增长的持续放缓，这一经济增长放缓的现象被称为“结构性减速”，支持这一观点的逻辑是中国服务业发展滞后，其生产率相对工业部门生产率较低，向“服务化”转变导致经济增长放缓。陆明涛等也认为，在劳动人口增长减缓甚至负增长、资本投资下降、要素产出弹性下降的冲击下，结构性减速不可避免。

2.出口结构和劳动生产率

发展中国家参与全球产业链分工，具备吸收发达国家技术实现劳动生产率快速增长的“后发优势”。卡茨(Kates)比较了1970—1996年期间拉丁美洲国家和美国的劳动生产率增速，拉丁美洲国家产业结构转向具备比较优势的原材料加工和劳动力密集型产业，使得这些产业的劳动生产率相比美国对应产业的劳动生产率差距减小，而其余产业的劳动生产率差距不断扩大。孙文远和姜德波认为，基于比较优势和规模经济利益的获得、技术进步和技术溢出效应、企业和产业组织创新效应等途径，参与产品内国际分工对劳动生产率的提高有积极作用。唐东波对中国2000—2006年参与全球分工的研究也发现，参与国际垂直分工对劳动生产率增长确实有正向作用，尤其对高新技术行业和低生产率企业的效应更大。

3.资本深化和劳动生产率

资本深化即劳动力人均资本不断增加的过程，根据Solow增长模型，当经济处于平衡增长路径上时，劳均资本是稳定的；对于发展中国家来说，储蓄率偏高和外向型发展战略都意味着资本深化的持续性。有学者通过对1987—2005年中国劳动生产率的分解，认为储蓄是这一期间劳动生产率持续增长的主要原因，而这与中国对外开放过程中资本深化持续加深相关；类似的，毛丰付和潘家顺也认为1995—2010年间资本深化对地级市及以上城市劳动生产率的贡献最大，尽管这一影响呈缓慢下降态势；李谷成也认为资本积累及其深化是改革开放以来中国农业持续增长的重要原因。

4.人力资本和劳动生产率

在内生增长理论中，知识和人力资本对全要素生产率的提高十分重要，进而影响经济的长期增长。在实证研究中，大多数学者使用教育人力资本作为代理变量，证实了人力资本提高对劳动生产率的促进作用。如费舍尔(Fischer)等人使用欧盟NUTS-2地区的观测数据，发现地区人力资本的相对提升对区域的劳动生产率确实有促进作用；兰加斯(Rangazas)对美国长期(1870—1970年)的劳动生产率研究表明，教育数量和质量能解释美国30%—40%的劳动生产率增长；其他的研究也表明人力资本对劳动生产率具有正向作用。

在现有关于中国劳动生产率的研究中，大部分学者从资本深化和要素结构转变的角度分析劳动生产率增长，少量研究考察了资本深化和教育人力资本的影响，前者忽视了中国经济发展过程中教育扩张的贡献，后者却没有考虑到结构因素的动态变化。此外，在研究教育人力资本对劳动生产率的影响时，大多学者仅考虑了教育数量而忽视了教育质量，虽然张海峰等估计了教育质量的影响，但是其使用的数据较早(1980—2005年)，不能反映出高等教育扩张的效应。综合已有文献，本文将考虑结构转变、资本深化和教育(数量和质量)人力资本对劳动生产率的边际影响和增长贡献。

三、分析框架

在对影响劳动生产率的因素进行实证分析时，主要使用的方法有两种，即回归和分解。回归的结果能直接反映在某一给定自变量的水平上，的微小变动对于因变量的影响，因此回归系数又被称为条件偏效应，回归系数即为均值处的偏效应。在某些情况下(比如研究性别收入差距和代际收入差异时)，为了测量的微小变动对于的边际分位数或者的边际分布的其他函数的影响，可以使用RIF(Recentered Influence Function)回归。

对被解释变量的变动进行分解，有助于清楚认识不同解释变量的增长贡献。在部分文献中，学者们对劳动生产率的研究专注于劳动生产率变动成因的分解，比如，法格伯格(Fagerberg)、佩内德(Peneder)、蔡跃州和付一夫等使用偏移—份额分解法将劳动生产率拆解为进步效应和结构效应。偏移—份额分解法对数据质量有一定要求，即需要知道各产业的投入和产出占比，在实证分析中，投入占比和产出占比数据往往由测算得出，存在一定缺陷。另一种新兴的分解方法是基于RIF回归，这一方法和Oaxaca-Blinder分解相似，但不同的是RIF分解研究的是要素及其回报的变化对在不同时期分布的影响。

本文将基于面板OLS回归探讨各要素对于劳动生产率的边际效应，使用RIF分解讨论引起不同阶段劳动生产率水平和分布变化的原因。下面介绍OLS回归模型和RIF分解方法。

1.生产函数和OLS回归模型

基于Solow增长模型，提出地区生产函数如下：

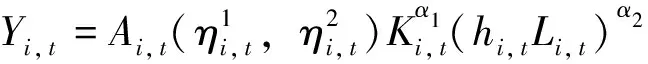
(1)

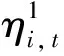
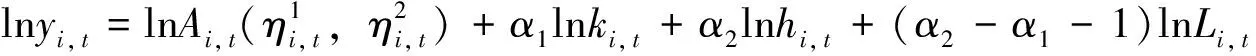
(2)

其中，,=,,，即为劳均产出，也称劳动生产率；,=,,，为劳均资本存量。

下面分别给出全要素生产率和人力资本的具体形式，设定为：

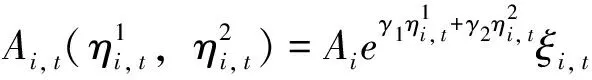
(3)

,=,+,-+(,,,-),

(4)

将方程(3)、(4)进行对数变换后代入方程(2)，可得到用产业结构、出口结构、劳均资本存量、教育数量、教育质量及总劳动力数量表示的劳动生产率增长方程:

·(,,,-)+,

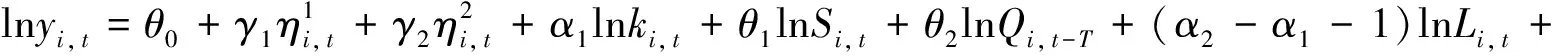
(5)

2.RIF分解

(6)

(,())=(,())+()

(7)

同样，也仅为的函数。在方程(7)等号两边求期望，得到如下方程：

[(,())|=]

(8)

根据方程(8)，统计量()等于的无条件期望，同时也等于的条件期望。这意味着把作为被解释变量，作为解释变量进行OLS回归，可以得到如下方程：

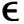
(9)

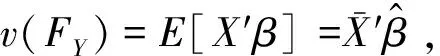
费尔南多(Fernando)基于菲尔波等人的工作，提出了使用半参数方法来确定反事实分布函数，并将分布函数的变化分解为系数效应和特征效应。在数据中，只能观察到受到影响后的分布函数，用表示反事实，设定的反事实分布函数。统计量的变动可以分解为：

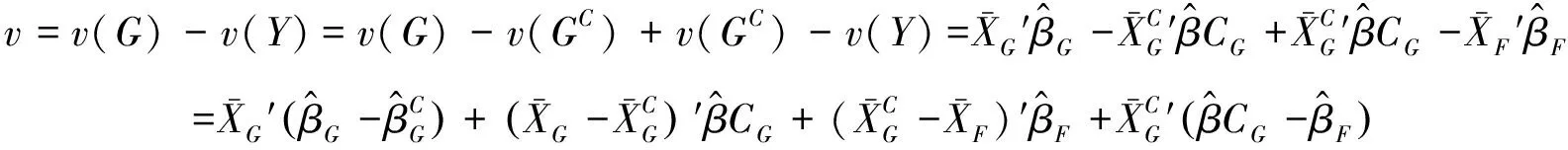
(10)

在式(10)中，最右边等号后第一项为纯系数效应(Pure Wage Structure)；第二项为权重分配误差(Reweighting Error)，用于重新加权策略的质量，在大样本下期望为0；第三项为纯特征效应(Pure Composition Effect)；第四项是模型误差(Specification Error)，用于评估模型设定和RIF估计的质量。第一项和第二项之和被称作系数效应(Total Wage Structure)，和Oaxaca-Blinder分解类似；第三项和第四项之和被称作特征效应(Wage Structure Effect)。

至此，本文提出了对劳动生产率阶段性变化特征的分析框架：使用OLS回归可以直观体现各要素对劳动生产率的边际影响；RIF分解可以用于讨论各生产要素对不同时期劳动生产率分布(统计量)变动的贡献大小。

四、数据来源和趋势性描述

本文使用的数据为1998—2019年各省(自治区、直辖市)宏观数据，文中所有的经济数据均按各地平减指数转换为1998年价格。下面根据各变量数据的收集和处理进行说明。

劳动生产率由各省(自治区、直辖市)的年末GDP与三次产业从业人员总数相比得到，数据均来自各省(自治区、直辖市)统计年鉴。图2是主要年份地区劳动生产率的核密度分布情况，从分布曲线的开口程度可以看出，地区间的劳动生产率差距有随时间缩小趋势，表现为后发地区对先发地区的追赶和趋同，这一现象也被称作经济发展的区域间溢出效应。

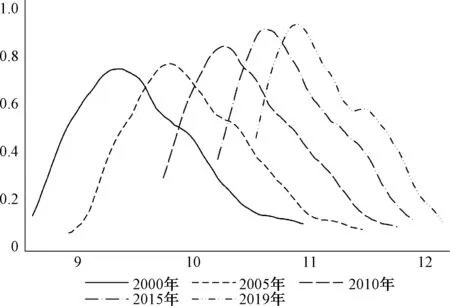
图2 主要年份劳动生产率(对数值)核密度分布

产业结构分为以工业产值与非农部门产值之比表示的“工业化”结构和以服务业产值与非农部门产值之比表示的“服务化”结构，本文使用“工业化”结构指标，数据来自各省(自治区、直辖市)统计年鉴。

按照孙永强和巫和懋的方法，出口结构被定义为各省出口总额中资本和技术密集型产品出口占比，他们选取了10个行业的数据；但是，各省在公布商品出口金额时采用的统计标准不同(分为SITC标准和HS标准)，且部分省份并未公布细分行业出口数据，给数据整合造成困难。基于上述原因，本文使用高技术产品出口金额占总出口的比重来表示出口结构，其中各地区高技术产品出口金额可由《中国高技术产品统计年鉴》和《中国科技统计年鉴》获取，总出口数据来自各省市统计年鉴。

劳均资本存量为各地区资本存量与从业人员总数之比。单豪杰使用永续盘存法计算了中国各省1952—2006年的资本存量(1952年价格)，基于此，本文按照折旧率为10.96%计算，并根据固定资产投资价格指数将各省资本存量测算至2019年(1952年价格)，再根据各省GDP平减指数将资本存量转换成1998年价格，再除以从业人员数即可得到1998—2019年各省劳均资本存量。劳动力数据来自各省市统计年鉴。

教育数量即各省从业人员平均受教育年限。根据《中国劳动统计年鉴》公布的“分地区从业人员接受教育程度分组构成”计算得到，具体而言，平均受教育年限=小学占比×6+初中占比×9+高中占比×12+大专占比×15+本科占比×16+研究生占比×19。

教育质量数据用生均教育经费支出表示，数据来自于《中国教育经费统计年鉴》，目前该年鉴系列已经公布1995—2018年教育经费支出数据。本文使用的教育经费数据包括各地生均教育经费支出(由总的教育经费支出除以该年在校学生总数得到)、普通高等院校生均经费支出和普通中学生均经费支出，均换算成1998年价格。

其他数据包括城镇化率、用就业占比表示的工业化结构，均来自各省市统计年鉴。表1给出了未经对数换算的样本数据的描述性统计。

表1 样本的描述性统计结果

五、实证分析

1.OLS回归

(1)基准回归。按照方程(5)，使用样本数据对各省(自治区、直辖市)劳动生产率进行回归估计，Hausman检验拒绝了原假设，因此使用固定效应模型，所有回归均控制了时间效应和地区固定效应，教育质量数据为三年平均值(滞后期和前后两年)，回归结果如表2所示。第(1)至第(9)列的结果表明，产业结构“工业化”对劳动生产率有十分显著的正向作用。从系数大小来看，产业结构对劳动生产率的边际影响至少为0.273，这意味着在均值处，工业部门产值在非农业部门产值中的比重每提高0.01，劳动生产率将至少提高0.273%；对应的，在边际影响上，服务业产值在非农部门产值中的比重每提高0.01，劳动生产率将至少降低0.273%。这一估计结果同“结构性减速”的观点相符。

表2 OLS回归结果

出口结构优化同样对劳动生产率有显著的促进作用。出口结构(高技术产品出口占比)每提高0.01，劳动生产率在边际上至少提高0.047%。随着中国劳动力成本不断上升，以劳动密集型产品出口为主的贸易结构将不可持续，中国开始实施创新驱动发展战略，鼓励支持企业创新，带动外贸出口产品向技术和资本密集型转变优化，在全球产业链分工中加速从下游转向中上游，高技术附加值产品出口占比增加，促进劳动生产率提高。

第(4)至第(9)列的结果表明，资本产出弹性在0.133—0.169间，低于其他大部分研究得到的结果。导致这一差异的可能性有：基期存量资本和固定资产投资测算不同，单豪杰未将土地、存货投资纳入固定资本投资中，因此得到的资本存量相对小，使用的折旧率不同，分省折旧率为10.96%，比其他大多数学者使用的折旧率要高；有的学者使用城市数据估计资本产出弹性；此外，样本所定的基年不同也会导致估计结果差异。

第(5)、(6)列的结果表明，教育数量和教育质量(滞后5年)的提升对劳动生产率都有显著的促进作用。加入交叉项后，尽管交叉项的系数对劳动生产率的促进作用仍然相当显著，但教育数量和教育质量各自的影响不再显著，这和模型的预测不符。主要是因为滞后5年的教育质量和教育数量并不匹配，2019年中国大陆劳动力平均年龄为38.8岁，因此使用滞后10年甚至更久的教育质量数据比较合理。使用滞后10年的教育质量数据，估计结果如第(8)和第(9)列所示，交叉项的系数为负，表明教育数量对劳动生产率的影响在一定程度上取决于教育质量：当教育质量较低时，扩大教育数量对劳动生产率的边际影响更大；随着教育质量的不断提升，教育数量扩张对劳动生产率的边际影响不断减小。在本文样本中,教育质量均值(对数值)为7.717，因此教育数量对劳动生产率的边际效应为0.425>0(0.425=0.888-0.06×7.717)，即教育扩张对劳动生产率仍有促进作用。

总结OLS回归结果，解释变量的估计系数基本符合模型预测(除资本产出弹性偏小)。值得说明的是，尽管产业结构对劳动生产率的边际影响较大，但从经济意义来看，产业结构的转变是一个长期且缓慢的过程，因此实际的影响大小还有待探究。

(2)稳健性检验。为了证明回归模型的稳定性，使用替代变量对第(9)列进行重新估计。表3是稳健性检验结果，用第二产业从业人员占非农部门从业人员之比表示产业结构，回归结果如第(10)列所示，对比表2第(9)列的估计结果，产业结构对劳动生产率的边际影响并无显著变化，但是教育质量的边际影响降低且教育数量和教育质量交叉项的回归系数在统计上变得不显著。在第(11)列中，用滞后10年的普通高等学校生均经费支出作为教育质量的代理变量进行回归，发现教育质量、教育数量和教育质量的交叉项对劳动生产率并无影响；对比之下，第(12)列中，用普通中学生均经费支出作为教育质量的代理变量，除出口结构对劳动生产率的边际影响在统计上不显著外，其余估计结果和第(9)列的结果十分相似。导致第(11)、(12)列的教育质量系数估计结果存在差异的可能原因是：普通高等学校的学生大多为“流动人口”，受教育地和就业地不一致。在第(13)列中，加入控制变量“城镇化率”，主要解释变量的估计结果相比第(9)列在统计上基本无差异。综上，本文的OLS回归结果比较稳健。

表3 稳健性检验

(3)分组回归。本文想说明在经济发展的不同阶段，解释变量对劳动生产率的影响是不一致的,正如部分学者指出的那样，2010年之后，中国的经济增长发生了“结构性减速”。将2010年作为经济增长模式的转折点，将样本进行分组回归，估计结果如表4所示。

表4 按年份分组回归

在表4中，第(14)、(15)列为使用2010年及其之前数据的回归结果。产业结构对劳动生产率的边际影响变小且仅在10%的统计性水平上显著；出口结构、教育质量对劳动生产率没有影响；对比之下，资本投入和教育数量投入对劳动生产率的影响较大且在统计上显著。这可能与1998—2010年期间中国劳动生产率的增长模式为要素投入驱动的粗放式增长相关。第(16)列为使用2011—2019年数据进行回归估计的结果，其中，产业结构对劳动生产率的边际影响为0.234，且在5%的统计性水平上显著；出口结构对劳动生产率无明显影响；劳均资本存量产出弹性仍然十分显著，且边际影响大小有所提升；对比第(17)列的估计结果，交叉项的系数减小且十分显著，这意味着2010年以后，在教育质量(教育数量)保持不变的情况下，教育数量(教育质量)边际生产率加快下降。整体上来看，2011—2019年期间，结构性因素对劳动生产率的影响开始提升。

2.RIF分解结果

(1)总体分解结果。在前面的分组回归中，以2010年为分界点(分别用和作为2010年前后时期的简称)，回归结果表明结构因素对劳动生产率的边际影响有较大差异，为了更进一步地认识要素投入和结构转变在经济发展不同时期对劳动生产率的影响大小，接下来使用RIF分解的方法进一步分析，表5是分解结果。

表5 RIF分解结果

在表5中，到期均值的总变动为正，对均值变动的分解结果表明，特征效应对均值总变动的贡献为73.8%，系数效应对均值总变动的贡献为26.2%。在特征效应中，纯特征效应几乎能完全解释特征效应的变动，这意味着不同时期解释变量的结构变动是造成劳动生产率均值变动的主要原因。尽管纯系数效应对均值变动的贡献超过100%，但是权重分配误差较大，导致系数效应对均值变动的贡献总体较小。

对方差总变动的分解结果表明，系数效应导致总效应变动为负，贡献度达到了177.88%。对系数效应进一步分解发现，纯系数效应为正，但权重分配误差较大导致系数效应为负。特征效应为正，但主要是模型设定误差导致的。对50%分位数和10%分位数之差的分解结果表明，系数效应造成了不同时期的差异为负，而权重分配误差解释了系数效应为负的原因；特征效应为正，但影响较小。不同时期90%分位数和50%分位数之差为负，主要为系数效应导致，而纯系数效应导致了系数效应为负；特征效应为负，但由模型设定误差所致，纯特征效应为正，对不同时期90%分位数和10%分位数之差的分解得到类似的结果。上述结果表明，时期，尽管解释变量的结构变动会导致劳动生产率分布更加发散，但系数效应的负向影响更大，使得劳动生产率分布更加集中。

表6展现了对均值进行分解时主要解释变量对四种效应的解释力度。在纯特征效应中，有51.43%可以由劳均资本存量变动解释；劳动力的纯特征效应为负，这与模型的预测一致；教育数量(教育质量)的纯特征效应受到教育质量(教育数量)的影响，且人力资本的纯特征效应为正；产业结构和出口结构对于纯特征效应的贡献非常小。在纯系数效应中，24.13%由产业结构的纯系数效应贡献，1.85%由出口结构的纯系数效应造成；教育数量(教育质量)的纯系数效应受到教育质量(教育数量)的影响，且人力资本的纯系数效应为正。简言之，劳均资本存量主要通过特征变化(投入增加)影响劳动生产率；人力资本(教育数量和教育质量)通过特征效应和系数效应(回归系数)影响劳动生产率；结构因素在对劳动生产率的增长影响中主要表现为系数效应，但贡献相对较小。

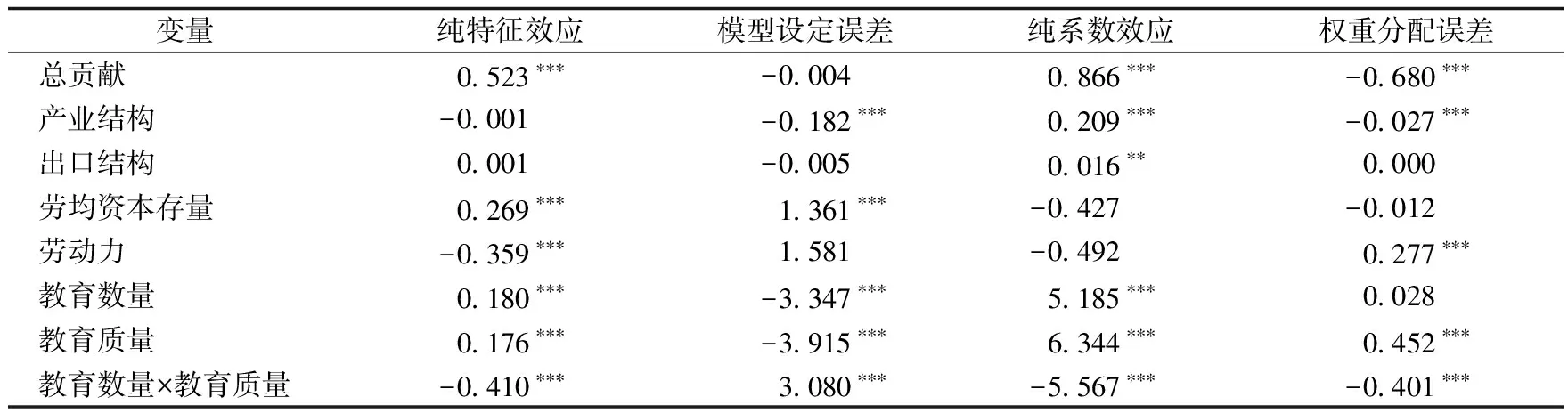
表6 解释变量对均值变动的贡献(RIF分解)

(2)分位数变动分解。将不同分位点上的劳动生产率变动分解成四种效应，结果如图3所示。总体上，纯特征效应对总变动的贡献最大；模型设定误差在中部分位区域相对较小,意味着在中部分位处模型设定相对更合理，RIF估计质量更高；纯系数效应对总变动的贡献基本为正，且在劳动生产率较低的分位处贡献更大；而权重分配误差的表现和纯系数效应相反。这些现象表明：在不同阶段，解释变量的特征变化是劳动生产率增加的主要推动力量；这也同时印证了对均值变动分解时得出的观点。

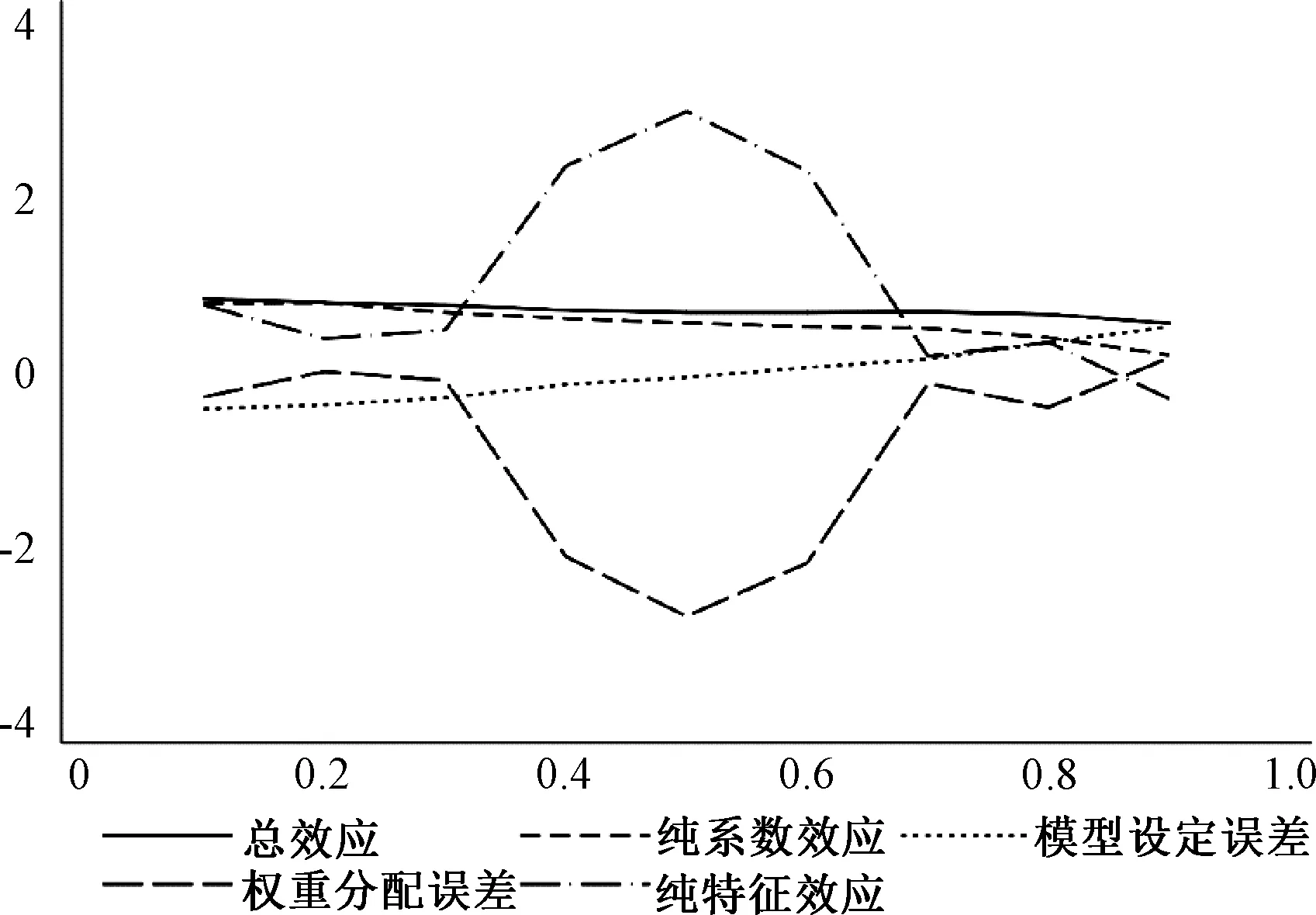
图3 分位数变动分解

图4描绘了产业结构和出口结构在不同分位数上的贡献大小。对产业结构的效应分解表明，特征效应主要解释了总效应。产业结构的效应在低分位数上的作用为负，在高分位数上的作用为正，即产业结构的服务化转变对高劳动生产率一侧有正向作用，对低劳动生产率一侧有负向作用。部分原因可能是制造业的“服务化”转型，即国内服务替代国外服务。对出口结构的效应分解表明，出口结构的效应在低分位数处为正，在高分位数处为负，但整体上效应较小。

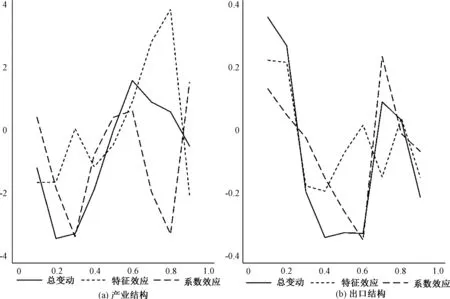
图4 结构因素在不同分位数上的增长贡献分解

六、总结与讨论

在中国经济发展迈入新阶段背景下，劳动生产率对经济的长期合理增长起着决定性作用，正确认识中国劳动生产率的增长过程将有益于深入理解新阶段的经济增长。本文在新古典增长模型的基础上，考虑结构转变、资本深化和人力资本对劳动生产率的边际影响和增长贡献。使用中国各省(自治区、直辖市)1998—2019年的数据进行OLS回归分析，并以2010年作为经济发展模式的转折点，对前后不同阶段劳动生产率水平和分布的变动进行RIF分解，得出以下五点结论：第一，OLS回归结果表明，产业结构“服务化”在边际上对劳动生产率有负向影响；RIF分解结果显示，产业结构“服务化”主要促使处于较低分位数上的劳动生产率增长减速，对处于较高分位数上的劳动生产率有促进增长作用。第二，结合OLS估计和RIF分解结果，出口结构对劳动生产率的边际促进作用仅发生在低分位数上，且总体效应很小。第三，相对于上一个时期(1998—2010年)，产业结构转变阶段资本产出弹性更大。分解的结果表明，资本深化是促进转变期劳动生产率增长的最重要的力量。第四，不论是从对劳动生产率的边际影响还是从对劳动生产率的增长贡献来看，教育数量和教育质量都存在相互影响。第五，转变期中国劳动生产率分布收敛，表明地区间劳动生产率的趋同，而这主要是系数效应(要素回报)形成的。

根据本文的研究结果，中国在经济转型期间确实经历了一定程度的“结构性减速”，但产业结构“服务化”也有积极的一面，即促进高劳动生产率部分的增长。“服务化”是中国经济发展在工业化后期必然经历的过程，引导生产性服务产业发展，促进制造业向高端化发展将缓解转变期之“经济阵痛”。未来应更加重视人力资本在劳动生产率增长中的重要作用。教育扩张仍然对劳动生产率的增长具有积极作用，但在扩张的同时也应兼顾教育质量。

本文的研究存在一定不足之处，即本文使用的资本存量数据并没有包括土地、存货等投资，但在中国经济的发展过程中，土地这一要素投入同样发挥着重要作用，因此可能会导致低估资本产出弹性。未来可以从产业结构对不同水平劳动生产率影响的差异开始，探究中国经济“服务化”发展的具体路径，评估产业结构转变对经济增长减速的贡献大小。