深水导管架时程动力响应分析技术

黄怀州，胡永明，袁玉杰，刘钊

（海洋石油工程股份有限公司设计院，天津 300457）

引言

上世纪60年代我国在渤海建造了第一座固定式导管架海洋平台，自此海洋石油勘探开发迎来了高速发展。随着海洋石油工业不断发展，海洋平台形式多样化，出现了半潜平台、顺应塔平台、张力腿平台、SPAR平台、FPSO等，但导管架平台仍然是我国现阶段海洋开发的主要形式。

目前我国在役的导管架平台主要分布在渤海、东海、南海海域，最大水深约200米。在世界范围内，已建成的超过200米水深的导管架平台共计13座，其中最深的位于墨西哥湾的Bullwinkle油田，平台水深412米。近20年来建成的水深超过200米的导管架平台共4座，见表1。

表1 近20年建成的水深超过200米的导管架平台

固定式导管架平台，作为浅海油气开发的平台结构形式，在环境适用性和工程经济性方面有着浮式平台不可比拟的优势。通常认为400米水深以内，导管架平台是海洋油气开发最合理和经济的平台形式。

一般典型浅水导管架平台的自振周期约1.5秒，深水平台的周期约3.5秒或更大[1]。随着水深的增加，平台结构的整体刚度越来越小[2]，低阶固有频率将接近波浪荷载的激励频率[3]，结构动力响应呈非线性增加[4]，对动力分析的精度要求更高。陆丰钻采平台水深达281米，是我国首个水深接近300米的导管架平台，采用随机波浪时程分析技术进行动力分析。

1 导管架时程动力分析流程

导管架设计时要考虑波浪荷载的动力效应，对于水深相对较浅的平台，可以通过设计波产生的静态波流力直接乘以动力放大系数来实现。对于深水平台，为了正确考虑惯性力在平台高度方向的分布，需要计算出等效惯性荷载，再与静态波流力组合。

深水导管架时程动力分析主要包含以下几个方面：

（1）随机波浪分析，根据海浪谱生成若干波浪时程，即荷载输入；

（2）动力响应分析，求解运动方程获得结构的响应，即结果输出；

（3）对结构响应历程进行统计分析，计算动力放大系数，生成惯性荷载并计算惯性荷载系数，即结果处理。

2 随机波浪分析

海洋中某一点的水面高度是在平均水平面附近随机变化的，它可以考虑为很多不同频率的简谐波叠加组合而成[5]。每个简谐波有不同的频率和幅值，而每个简谐波的相位是随机的且与频率无关。以y(t)表示水面高度随时间变化的时程：

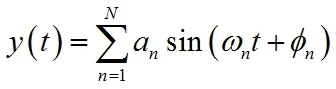
随机波浪常用波谱来描述，常用的波谱有Pierson-Moscowitz谱和Jonswap谱。

Pierson-Moscowitz谱：

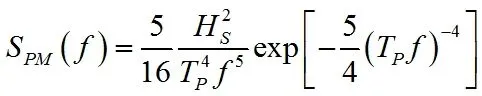
式中Hs为有效波高，Tp为谱峰周期。

Jonswap谱[6]：

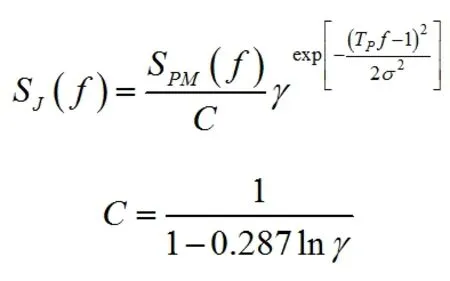
式中C、γ、σ为无量纲参数。当γ=1，Jonswap谱与PM谱相同。

给定波浪谱具体参数后，可以方便的计算出各简谐波的频率和幅值。比如将连续的波浪频谱分割为等宽度的n个离散频率带，每个频率带下包含的面积即为该频率波浪的能量。

图1 波谱离散

fn=nf1

Ωn=2πfn

选择一组随机数作为各简谐波的初相位，便获得一个波浪时程。为了使模拟的随机波浪能够代表设计环境条件，需要对波浪时程进行筛选，筛选条件一般包括以下几个方面：

（a）最大波峰高度在0.9～1.1倍有效波高之间；

（b）最大波高不小于环境数据给出的设计波最大波高；

（c）最大波高发生时刻远离时程的开始与结尾。

3 动力响应分析

3.1 运动方程

结构动力响应计算的主要内容就是求解运动方程，对于多自由度体系，运动方程可以表示为矩阵形式：

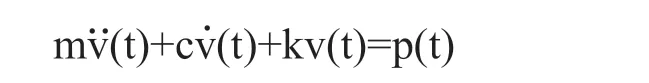
其中v(t)和p(t)分别为节点位移向量和荷载向量，矩阵k、c和m分别为结构的刚度矩阵、阻尼矩阵和质量矩阵。

应用振型叠加法可以将耦合的多自由度运动方程变为 个非耦合的单自由度运动方程：

3.2 逐步积分法

使用振型叠加法需要结构体系保持线性，而逐步积分法可以高效的求解非线性问题。它把响应的时程划分为一系列短的、相等的时间步，对每一个时间步按照线性体系来计算其响应。非线性多自由度分析就近似为一系列依次改变特性的线性体系分析[7]。在一个时间步内，运动方程转化为增量形式：

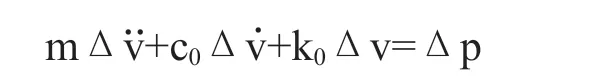
其中c0和k0为时间步起始时刻的阻尼阵和刚度阵，Δv和Δp为位移和荷载增量。

通过假定加速度向量随时间的变化方式就能方便地建立起位移、速度和加速度之间的关系式。最简单的积分方法是Euler-Gauss方法，假设加速度在时间步持续时间内为固定常数，且等于时间步初始及结束点加速度的平均值，因此也称为常平均加速度法。

当采用常平均加速度法时，方程转化为：

进行逐步分析时，首先由时间步起始时刻的条件确定的质量、阻尼和刚度特性计算Kc，并从阻尼性质和这步开始时刻的速度、加速度及荷载的增量计算ΔPc，然后求解方程计算出位移增量Δv。在非线性分析中，k0和c0变化要求每一个时间步都必须进行计算，而对于线性分析，k0和c0值保持不变，计算得到简化。

位移增量确定后，由基于常平均加速度假设的表达式求出速度增量：

重复以上步骤即可逐步求解结构的响应历程。

4 结构响应统计分析

4.1 动力放大系数

对于深水导管架平台，通过详细的动力分析计算出平台在随机波浪荷载作用下的响应，再对平台响应进行统计分析[8-11]，计算动力放大系数。

目前国内导管架平台设计时，以平台整体基底剪力为研究对象。对每个响应时程，计算动力与静力最大基底剪力的比值，再将所有响应时程的比值取平均作为动力放大系数。随着水深的增加，环境荷载引起的弯矩将成为平台结构设计的控制因素。动力放大系数有必要考虑基底弯矩的影响：

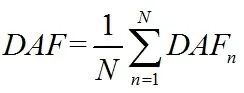
4.2 惯性荷载系数

由于基底剪力和弯矩分别计算了动力放大系数，需要两组（平台正交方向如0°、90°）或四组（平台斜向如45°、135°）惯性荷载及对应的惯性荷载系数。惯性荷载可以分别对平台X、Y方向前两阶弯曲振型施加平动加速度获得。结合静力分析生成的波流力，通过求解二元一次方程组，获得惯性荷载系数[12]。

X方向：

Y方向：

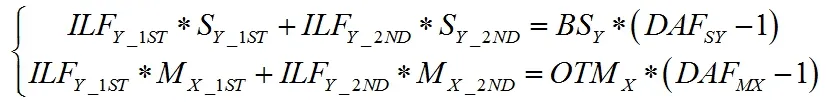
X方向参数说明（Y方向类似）：

ILFX1ST,ILFX2ND：惯性荷载系数，对应于X向第一、第二阶弯曲振型；SX1ST,MY1ST,SX2ND,MY2ND：X向第一、二阶振型惯性荷载对应的剪力和弯矩；DAFSX,DAFMY：X向动力放大系数，分别对应基底剪力和基底弯矩；BSX,OTMY：静力分析波流力产生的基底剪力和基底弯矩。

5 陆丰导管架动力分析实例

陆丰钻采平台，水深281米，主结构4腿12裙桩，顶部2层变为8腿支撑上部模块，上部模块操作重17000吨。百年一遇环境条件见表2，采用SACS软件建模和计算。平台前5阶自振周期见表3。

表2 百年一遇环境条件

表3 平台自振周期（秒）

经过筛选，选择符合Jonswap谱的20组波浪时程进行时程动力响应分析，每个时程持续1024秒，主要参数汇总如下：

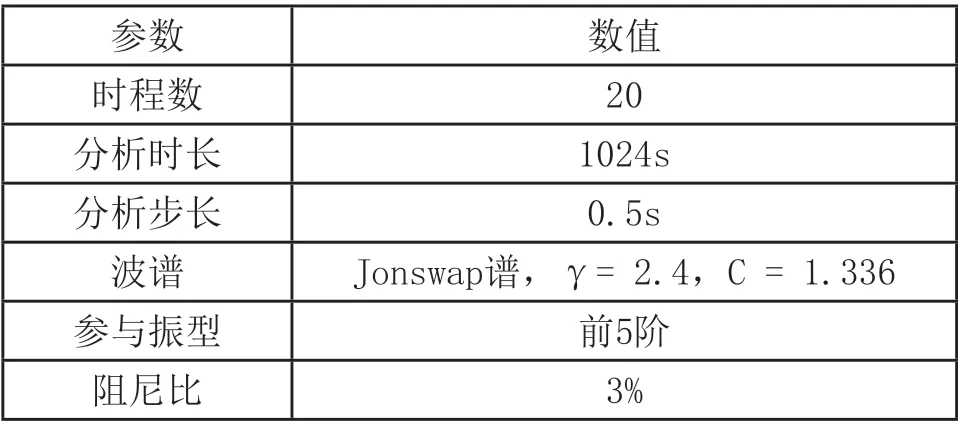
表4 动力响应分析参数

通过动力响应分析获得平台基底剪力和弯矩的响应曲线，典型的响应曲线见图2。

图2 平台基底剪力响应曲线

计算出0°、45°、90°三个方向动力放大系数：

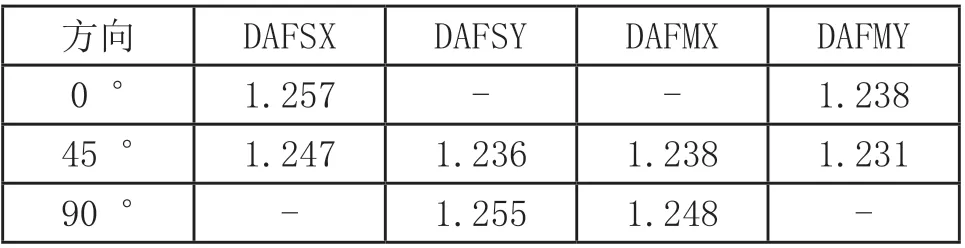
表5 动力放大系数

通过SACS软件静力分析模块计算波流力，通过RIGID模块计算惯性荷载，结果见表6和表7。

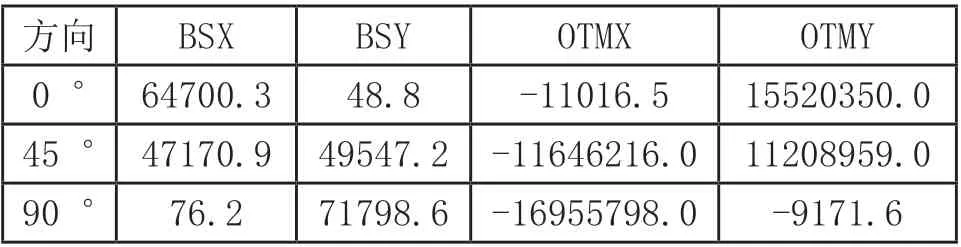
表6 静力波流力(KN或KN-M)

表7 惯性荷载(KN或KN-M)

求解方程组计算出惯性荷载系数，见表8。

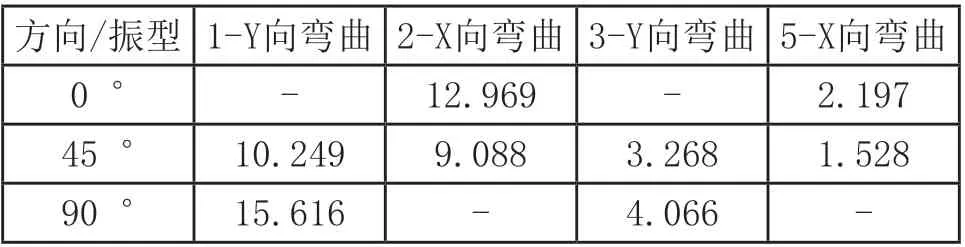
表8 惯性荷载系数

6 结论

采用随机波浪时程分析方法对我国第一座水深接近300米的导管架平台进行了动力分析，获得了平台的动力特性，主要得出如下结论：

(1)通过动力响应分析获得动力放大系数及惯性荷载，与静力分析得出的极端波流力组合后进行强度校核，是深水导管架平台工程设计中广泛采用的方法。相比于波流力直接与动力放大系数相乘，惯性荷载能准确反应出荷载在平台高度上的分布。

(2)应用随机波浪理论，通过海浪谱建立波浪时程，能够模拟平台在实际海洋环境中的响应，结果比确定性分析更加准确。为了使波浪时程能够代表设计环境条件，如百年一遇工况，有必要对时程进行筛选。选择20至30组时程，使计算结果平均值趋于稳定。

(3)陆丰钻采平台第一阶自振周期接近5秒，动态响应和静态响应峰值几乎同时出现，荷载与响应没有明显的相位差，采用惯性荷载与静力分析极端波流力组合的方法可以满足工程设计的需要。

(4) 随着水深的增加，同样的水平环境荷载将产生更大的基底弯矩，为了准确计算平台荷载，有必要分别计算基底剪力和弯矩的动力放大系数。对于陆丰钻采平台，如果动力放大系数仅考虑基底剪力，基底弯矩的计算误差约为静力波流荷载的3%，动力放大系数越大则误差越大。