基于微分博弈的三级供应链质量改进和广告宣传策略研究

□ 廖长华

(江南大学 商学院,江苏 无锡 214122)

1 引言

随着市场经济的快速发展，低层次的价格已经不能满足激烈的市场竞争需求，企业一方面需要加大研发投入，不断提升产品质量；另一方面要增加产品的广告宣传投入，提升品牌的形象和市场占有率，以此来获得竞争优势。市场需求是由多个影响因素决定的，不仅与产品的市场定价有关，还受产品的质量和营销策略影响。产品质量受生产企业所采用的生产技术的影响，也受供应商所提供原材料的质量的影响；营销策略主要有制造商进行的全国性广告宣传和零售商进行的地方性广告宣传。供应链上下游企业合作有利于扩大市场需求，例如，华为是一家生产销售通讯设备的通信科技公司，涉及手机、电脑等众多高科技产品，由于其积极从事产品创新、科技创新，于是作为华为手机屏幕的供应商三星也致力于产品质量改进，以保障最终产品质量的提升。华为通过全国性的广告宣传提高产品知名度，同时国美和苏宁等电子产品零售商也通过广告向客户介绍了产品特征，对产品进行一定力度的广告宣传。可见在供应链环境下，企业可以通过质量改进和广告宣传来扩大市场需求，增加收益，但这需要供应链上下游企业的共同参与[1]。

目前，供应链质量管理和广告策略作为供应链运营的关键问题，受到国内外学者的普遍关注。在供应链质量管理方面，Xie等结合Nash非合作博弈，设计了一种质量改进策略的选择机制，研究在同一细分市场中两个互相竞争的供应链的质量改进问题[2]。Fu等研究了在供应商领导、制造商领导和Nash模型下供应商对制造商投资进行产品质量改进问题[3]。Lu等研究了潜在品牌危机的供应链，比较危机前后制造商的质量策略和全球广告策略，评估危机造成的短期和长期损失[4]。朱立龙等研究了两级供应链中质量控制契约设计问题，生产商对其生产过程投资水平进行决策确定其产品质量预防水平，购买商进行质量评估决策并确定其产品质量检验水平[5]。吴双等研究了短期经济收益和长期质量声誉对合作效用的综合影响，设计了一类复杂产品供应链质量改进成本分担契约，在保障供应链收益的同时实现合作主体综合效用共赢[6]。洪江涛和黄沛以一个制造商和供应商构成的两级供应链为研究对象，应用微分博弈的方法分析了四种不同的质量管理博弈情形[7]。李坚飞等从创新驱动质量的动态视角出发，运用演化博弈方法构建多主体协同的动态演化博弈模型，分析新零售服务供应链协同质量改进中各参与主体的博弈策略选择[8]。贾晓霞等以三级供应链为研究对象，引入微分博弈的方法，研究4种不同的乳制品质量管理博弈情形下的质量改进和广告策略[9]。孙建慧等以三级装备供应链为研究对象，构建三种博弈模型，对装备制造企业的质量管理行为的协调问题进行研究[10]。

广告已经成为供应链成员提高整体消费需求的商业策略之一，广告宣传成本的分担成为协调供应链成员利益的重要策略。Seyedesfahani等研究了需求受制造商和零售商的广告策略和价格影响的供应链，并从Nash、Stackeberg-制造商、Stackeberg-零售商以及合作广告策略4个角度探讨了渠道成员间的定价和广告策略[11]。Dan等研究了在一个制造商和多个零售商组成的两级供应链中，制造商和零售商之间的混合广告合作问题，并提出了总利润分配策略[12]。Chen对制造商与零售商组成的两级供应链报童模型进行研究，将订购策略、地方性广告和品牌形象投资作为因素，研究表明在合作广告情形下，供应链整体利益优于非合作情形[13]。Huang等分析了在以制造商为主导的斯塔伯格博弈、纳什博弈和广告合作博弈3中情形下，制造商和零售商之间不同的广告策略和成本分担比例[14]。Yue等研究了当制造商向客户提供价格折扣时，制造商与零售商供应链中的合作广告策略的协调[15]。Taboubi研究双边垄断中的价格和广告协调问题[16]。Szmerekovsky研究了制造商和零售商之间的定价决策和双层广告水平，结果表明制造商在全国范围内进行广告宣传并向零售商提供较低的批发价格有利于供应链利润的增加[17]。李涛与刘斌以具有代替性的同质产品的竞争性供应链为研究对象，探讨成本共享比例内生和外生对合作广告协调的影响[18]。

综上所述，与现有的供应链质量管理文献相比，考虑到质量形成的长期性和动态变化特点，以及广告宣传对供应链管理的影响，本文通过引入微分博弈的方法从动态角度对三级供应链上的质量管理和广告宣传进行研究，系统分析供应商、制造商和零售商在Nash非合作博弈、Stackelberg主从博弈和集中决策情形下的供应链成员的最优质量管理行为、广告策略和供应链利润情况，从而探讨如何建立一种最优的供应链质量和广告协调机制，以期为产品质量的提升和供应链整体收益的增加提供科学指导。

2 模型假设

2.1 问题描述

本文以三级供应链作为研究对象，研究由一个供应商、一个制造商和一个零售商组成的三级供应链的动态质量改进和广告宣传问题。随着市场竞争越来越激烈，企业想要在激烈的竞争市场中占有一席之地，必须不断提升产品质量，扩大市场需求，而最终产品的质量不仅受制造商对产品研发、加工以及装配质量的控制，同时供应商所提供的原材料质量也会影响最终产品的质量。除此之外，产品的市场需求还会受到制造商和下游零售商对产品的广告宣传的影响。基于此，为进行三级供应链质量和广告管理研究，本文构建由一个供应商、一个制造商和一个零售商组成的三级供应链系统，如图1所示。

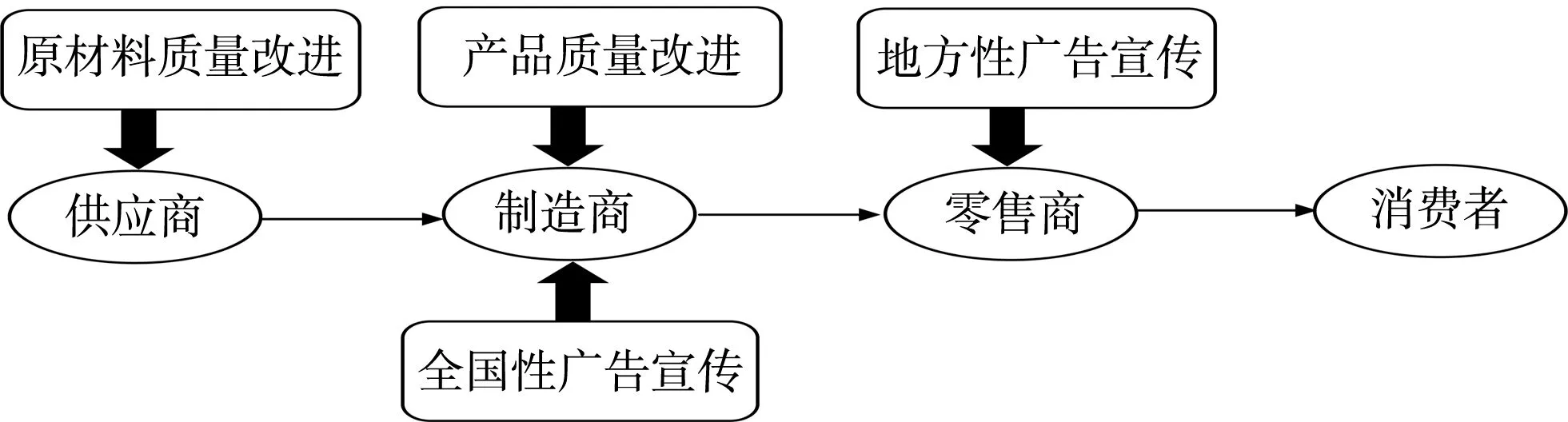
图1 三级供应链系统

2.2 符号说明

本文模型构建过程中所用到的符号如表1所示。

表1 符号定义

2.3 基本假设

本文假设条件如下：

①与众多学者类似，假设供应商质量改进成本CS和制造商质量改进成本CMQ是关于产品质量改进努力程度的凸函数，因此假设质量改进成本为

②零售商广告宣传成本CR和制造商广告宣传成本CMA是关于产品广告宣传努力程度的凸函数，因此假设广告宣传成本为

③产品的质量是动态变化的，产品质量的变化受当期制造商和供应商原材料质量改进努力程度影响，由式(1)所示的动态方程表示：

Q(t)=α1Qs(t)+α2QM(t)-δQ(t)

(1)

式中，α1≥0,α2≥0分别表示供应商原材料质量改进努力和制造商质量改进努力对产品质量的影响程度；δ>0表示由于设备老化、技术落后等原因造成的供应链质量的相对衰减率，即质量衰减系数；Q(0)=Q0≥0表示初始时刻产品质量。

④市场需求取决于产品质量和制造商的全国性广告宣传和零售商地方性广告宣传的努力程度的线性组合，所以我们假设：

D(t)=D0+θ1Q(t)+θ2AM(t)+θ3AR(t)

(2)

其中,D(t)为时刻市场需求；D0为潜在市场需求；θ1表示产品质量水平对市场需求的影响系数，θ2和θ3分别表示制造商和零售商广告宣传对市场需求的影响系数。

⑤供应商、制造商和零售商都是基于完全信息进行理性决策，不计供应链存货成本和缺货成本，在无限时间范围内，供应商、制造商和零售商在任意时刻均具有相同的折扣因子p>0。制造商对供应商质量改进成本的补贴比例为λs(t)，制造商对零售商的广告宣传成本的补贴比例为λR(t)，目标函数均为无限时间下的利润最大化。

⑥模型中所有参数α1、α2、θ1、θ2、θ3、θ4、Ks、KMQ、KMA、KR等都是与时间无关的常数。

3 分散式决策

3.1 Nash非合作博弈

假设制造商、供应商和零售商地位平等，同时行动、独立决策以实现自身收益最大。此时，理性的决策者将不会为其他企业分担质量改进成本和广告宣传成本，故在本情形下有λs(t)=λR(t)=0，因此，供应商S、制造商M、零售商R的决策问题分别为

结论1：Nash非合作博弈情形下，供应商、制造商、零售商最优策略为

(3)

证明：假设供应商、制造商和零售商各自的最优收益函数为VS(Q)、VM(Q)和VR(Q)，其中应满足如下哈密尔顿-雅可比-贝尔曼(HJB)方程，即

(4)

(5)

(6)

使式(4)(5)(6)最大化成立的必要条件是等号右边一阶偏导数为零，整理可得：

(7)

将式(7)代入哈密尔顿-雅可比-贝尔曼(HJB)方程中，整理得：

(8)

(9)

(10)

根据式(8)-(10)的结构特点，最优利润值函数Vs(Q)、VM(Q)和VR(Q)线性解析式可假设为

(11)

其中,a1、a2、a3、b1、b2、b3为待定参数。将值函数及其一阶倒数代入式(8)-(10)，并进行整理，把等式两边的同类项进行比较，并进行求解可得：

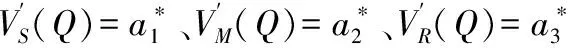
结论2：Nash非合作博弈情形下，供应商、制造商、零售商和供应链的最优收益分别是

(12)

3.2 Stackelberg博弈

假设制造商是供应链的领导者，供应商和零售商是跟随者，供应链成员以各自收益最大化为目标进行独立决策，决策时依照主从关系进行。首先，制造商确定自身质量改进努力程度QM及广告宣传投入AM，同时，确定对供应商质量改进成本分担比例λS、对零售商广告宣传成本分担比例λR，接着供应商和零售商观察到制造商的决策结果后，选择自身的质量改进努力程度QS和广告宣传努力AR。

则供应商、制造商、零售商的决策问题分别为

结论3：Stackelberg主从博弈情形下，三级供应链中供应商、制造商和零售商的最优策略分别是

(13)

证明过程和Nash非合作博弈情形下相同，这里不再赘述。

推论2：当满足2πM>πS、2πM>πR时，制造商才愿意承担供应商原材料质量改进成本和零售商广告宣传成本，否则制造商不会承担部分成本，反而还会向供应商和零售商收取一定的费用。

结论4：Stackelberg主从博弈情形下，供应商、制造商、零售商和供应链的最优收益分别是

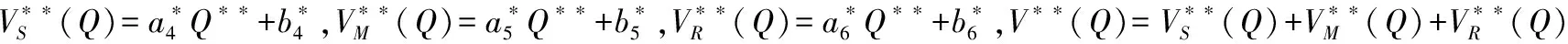
(14)

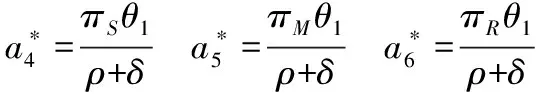
4 集中决策情形

此情形下，三方以供应链系统总利润最优为原则，共同确定QS、QM、AM和AR的值，此时供应链系统的决策问题为

(15)

结论5：在集中决策情形下，三级供应链中供应商、制造商和零售商的最优策略分别是

(16)

证明过程和Nash非合作博弈情形下相同，这里不再赘述。

结论6：在集中决策情形下，三级供应链的最优收益是

(17)

证明：将式(16)代入式(1)中得：

Q′=A***-δQ

5 比较分析

当2πM>πS、2πM>πR时，整理上述不同决策情形下的最优质量改进努力程度、最优广告宣传努力程度和最优利润函数得到表2。

表2 不同情形下最优决策对比

证明：当2πM>πS、2πM>πR时

V**(Q)-V*(Q)>0

集中决策与Stackelberg主从博弈情形的比较同上述证明过程。

①不同决策情形下制造商质量改进努力程度、广告宣传努力程度比较。

②不同决策情形下供应商质量改进努力程度、零售商广告宣传努力程度比较。

③不同博弈情形下供应商、制造商、零售商以及整条供应链系统最优利润比较。

当2πM>πS、2πM>πR时，在分散决策下，Stackelberg主从博弈与Nash非合作博弈相比较，供应商、制造商和零售商的最优收益及供应链整体收益均得到改善，实现Pareto改进。在集中决策下，供应链成员不再局限于自身收益的大小，而是以供应链整体收益最大化为目标进行决策，因而实现供应链整体收益的增加，达到Pareto最优。

6 算例分析

为了直观地表述供应商、制造商、零售商在不同决策情形下最优质量改进量、广告宣传投入和最优收益水平的比较分析结果，根据前文假设以及对参数的要求，算例相关参数取值如下：πS=3;πR=2;πM=6;KS=5;KMQ=6;KMA=5;KR=7;δ=1;D0=100;θ1=4;θ2=3;θ3=4;α1=6;α2=3;ρ=0.8,Q0=2。

首先，将参数代入相关命题，利用Matlab可以得出产品的质量改进量是如何随时间的变化而变化的，如图2所示。

分析图2可以发现，集中决策情形下产品质量改进量最大，其次是Stackelberg主从博弈情形，Nash非合作博弈情形下质量改进量最低。从中还可以发现，不论在集中决策还是在分散决策状态下，随着时间的变化，产品的质量改进量逐步上升，但是上升的速度越来越慢，最后收敛于均衡状态，从而能够得出产品的质量改进量如果受到外部环境的影响会发生一定程度的变化，但是随着时间的发展，产品质量改进量会趋于平稳状态。由图3可知，供应链中供应商、制造商和零售商的利润随着时间趋于平稳，最后稳定在某一值。从图4可以看出，在不同决策情形下，供应链整体的利润都随着时间增加，最后稳定在某一值。集中决策情形下供应链整体利润最大，其次是Stackelberg主从博弈情形下，Nash非合作博弈情形下质量改进量最低。

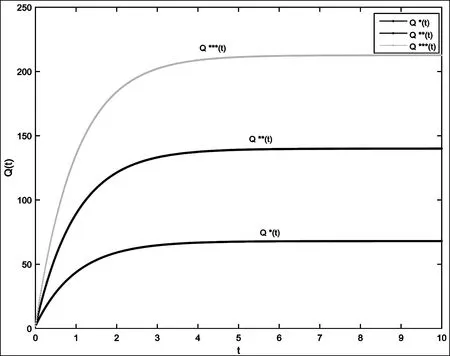
图2 三种决策情景下供应链产品质量改进量的比较分析

图3 分散决策下不同主体最优收益的比较分析

图4 三种情形下供应链整体收益的比较分析

7 结论

本文考虑到产品质量改进量的连续性，引入时间因素，从动态角度将微分博弈的方法应用到三级供应链的质量改进决策中，同时考虑到广告宣传对于产品销售也具有重要影响，构建了考虑广告宣传策略的三级供应链动态质量改进模型。文中重点分析了Nash非合作博弈、Stackelberg博弈和集中决策三种情形下，供应商和制造商的最优质量改进努力程度、制造商和零售商的最优广告宣策略、供应链成员收益和供应链系统总收益，通过比较分析和数值模拟可以得到以下结论：

①Nash非合作博弈和Stackelberg博弈情形下，制造商的质量改进努力程度和广告策略相同，但是Stackelberg博弈情形下，供应商质量改进努力程度、零售商广告宣传努力程度、供应链成员的收益水平都高于Nash非合作博弈情形，可以表明成本分担机制实现帕累托改进，符合企业发展现状的供应链合作机制；在集中决策下，供应链成员决策行为达到最优，系统收益最大，达到帕累托最优状态。

②随着时间的推移，最终产品的质量改进量逐步上升，上升的速度越来越慢，最终收敛于一个稳定值，说明产品质量改进量在受到外部环境影响时会发生一定程度的变化，但是随着时间的推移，产品的质量改进量会逐渐达到一个均衡状态。

③供应商和制造商的质量改进量和质量改进努力程度与质量改进量影响系数α1和α2、质量对需求的影响系数θ1、边际利润πS和πM正相关，与企业产品质量改进量的自然衰退率δ、成本系数KS和KMQ、贴现率p负相关；制造商和零售商广告宣传努力程度与自身边际利润πM和πR、广告宣传对需求的影响系数θ2和θ3正相关，与成本系数成本系数KS和KMQ负相关。企业可以通过扩大质量影响程度、增加边际收益、降低管理成本、研发质量改进新技术等措施来改善质量水平；并通过扩大广告影响程度、增加边际收益、降低管理成本来提高广告宣传水平。

本文重点研究在考虑广告宣传策略下的三级供应链质量改进问题，为了便于计算与推导，对模型和参数进行了简化，以后可以将价格纳入到模型当中，求解三级供应链动态质量改进和供应链成员的最优决策。本文仅研究了由一个供应商、一个制造商和以一个零售商组成的三级供应链的质量改进行为和广告宣传协调问题，而现实情况中供应链网络可能具有多个供应商和零售商，如何进行质量改进和广告宣传也是值得研究的方向。