精密零件的工业CT图像测量方法
吕 健,栾传彬,张秀英,蔡玉芳
(1.中国航发南方工业有限公司,株洲 412002;2.重庆大学 工业CT无损检测教育部工程研究中心,重庆400044)
工业计算机断层成像(工业CT)是一种以不同物质对射线的衰减不同为原理来获取物体内部结构信息的无损检测技术,在我国重要行业关键零部件的无损检测和质量评估中发挥着重要作用,其中利用工业CT技术实现重要行业精密零件的高精度测量是目前工业CT领域研究的难点和热点[1]。
随着科技的进步,传统划线剖切测量方法已不能满足精密零件的测量需求。基于工业CT图像的测量方法是解决精密零件测量难题的一个重要技术手段。针对CT图像测量的问题,国内外研究人员进行了大量的相关研究。CT图像测量方法分为半高宽法[2-6]、模板匹配法[7-13]和亚像素边缘检测法[14-17]。其中,半高宽法是以CT图像沿尺寸测量方向灰度值曲线的波峰与波谷的中间点作为被测零件与背景的分界点进行尺寸测量的方法[2-3],半高宽法具有原理简单、直观易操作、计算效率高等特点,大多测量仪器均是依据半高宽来进行尺寸测量的,其不足是随机误差大且受测量对象尺寸的限制[6];模板匹配法是根据两个不同大小图像之间的相关系数进行特征判别的模式识别方法[7],已广泛用于工业零件内部尺寸的检测[8-10]和医疗CT中疾病的诊断中[11-12];亚像素边缘检测法是由CT图像进行亚像素边缘定位从而实现几何元素测量的方法,典型的亚像素边缘检测算法有图像矩[13]、facet模型[14-15]、Bertrand模型[16]以及区域可伸缩拟合能量最小化模型等(RSF)[17]。RSF有良好的局部特性,不仅边缘定位精确高,而且轮廓连续性好,是目前主流的图像分割算法。
文章采用课题组提出的联合小波变换(WT)和RSF模型的图像分割方法[17](以下简称WT-RSF),实现精密零件CT图像亚像素级的分割,并采用最小二乘拟合法和最小距离搜索法实现直径、角度和壁厚等3种几何要素的测量,测量精度总体优于国际主流图像测量软件VG Studio Max 3.0(简称VG)的精度,有望为相关软件的自主开发奠定算法基础。
1 方法描述
1.1 WT-RSF图像分割算法
WT-RSF算法由小波降噪和RSF模型图像分割两部分组成。其中,小波降噪过程分为小波正变换和反变换两个过程,分别如式(1),(2)所示;RSF图像分割模型如式(3)所示,WT-RSF图像分割模型的详细描述见文献[17]。
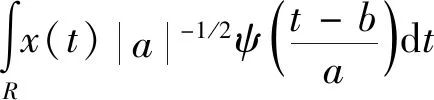
(1)

(2)
式中:a为尺度因子;b为伸缩因子;t为时间;R为平方可积空间;x(t)为待分析信号;ψ(t)为基本小波函数;fcwt(a,b)为信号x(t)的小波变换;Cψ为小波基函数的允许条件常数。
设x为灰度图像Ω中的一个点,x∈Ω;C为图像Ω中的一条闭合曲线,将图像Ω分为两个适应子区域Ω1和Ω2;f1(x)与f2(x)分别为这两个区域中以x为中心点的小区域内亮度的近似值,则RSF模型的拟合能量定义为
ν|C|
(3)
式中:|C|为轮廓长度;ν为长度项权重系数。
1.2 几何元素测量方法
进一步采用最小二乘拟合和最小距离搜索法[18]分别求取图像中圆的直径、直线夹角和型腔壁厚;对圆和角度拟合参数求解公式进行推导。
设待测圆的方程为
(x-x0)2+(y-y0)2=R2
(4)
式中:R为圆的半径;(x0,y0)为圆心坐标。
将式(4)展开有

(5)
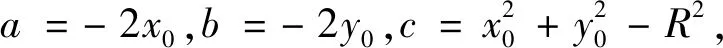
x2+y2+ax+by+c=0
(6)
求出参数a,b,c后,即可得到圆心(x0,y0)和半径R等参数

(7)
经图像分割并提取待测圆周的轮廓后,圆周上点(xi,yi)到圆心的距离di可表示为
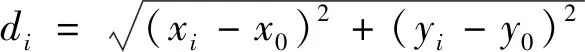
(8)
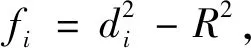
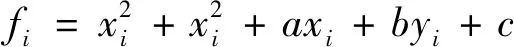
(9)
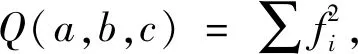
(10)
根据最小二乘拟合原理,当Q(a,b,c)取得最小值时可求解得到参数a,b,c,进而由式(7)求得圆心坐标和半径R,从而得到待测圆的直径。
同样,采用最小二乘法拟合直线方程yi=kixi+bi,i=1,2,即可求解待测角度
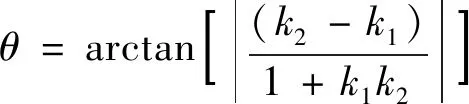
(11)
CT图像测量算法流程如图1所示,具体过程如下。
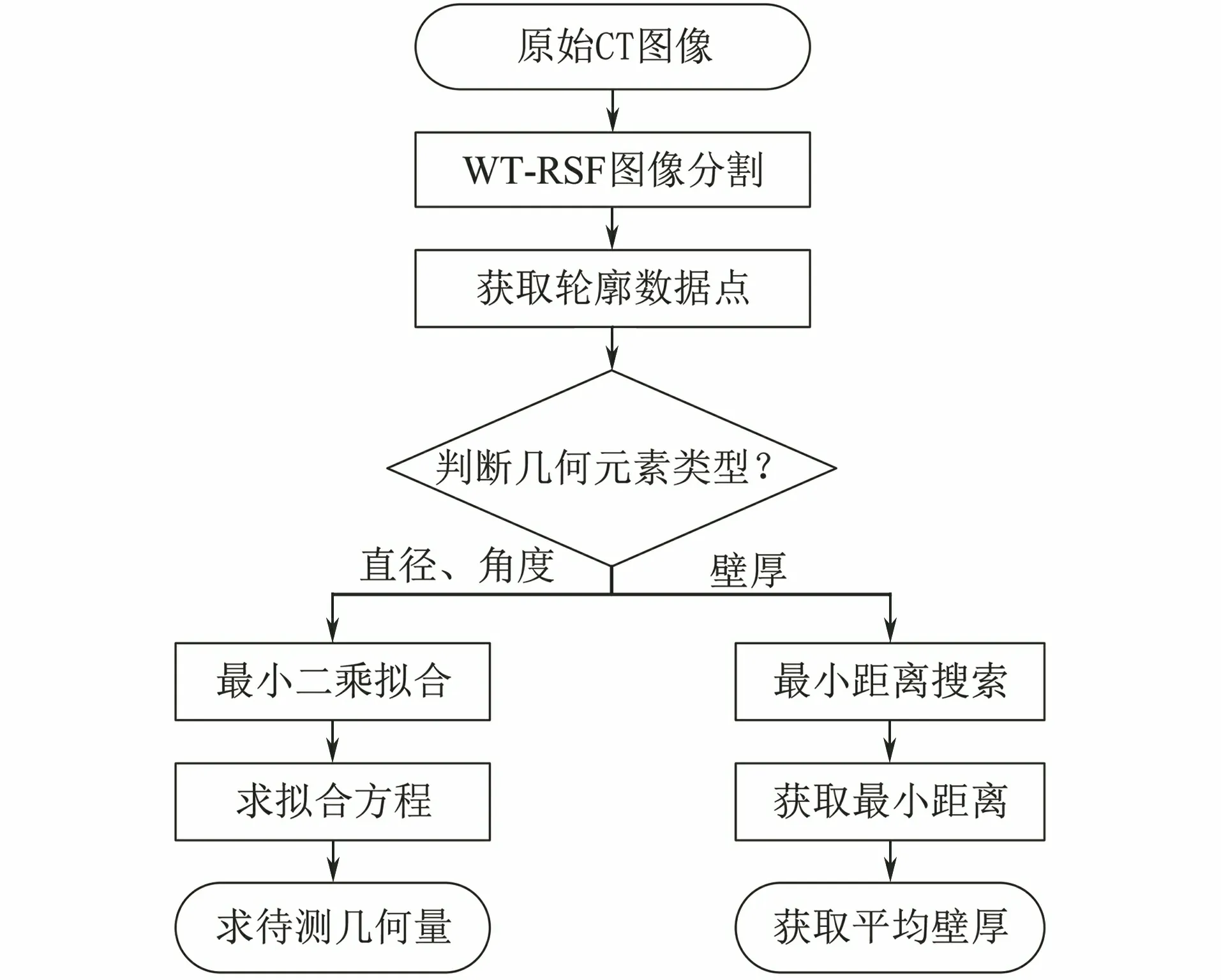
图1 CT图像测量算法流程图
(1) 采用WT-RSF方法分割精密零件工业CT图像并提取感兴趣的几何元素轮廓。
(2) 当待测元素为圆或角度时,采用最小二乘法拟合得到圆的方程或直线方程。
(3) 通过圆或直线方程计算待测圆直径或两直线间的夹角。
(4) 当待测尺寸为壁厚时,则采用最小距离搜索法测量待测位置的最小壁厚,并在待测位置的邻域搜索最小壁厚,取其平均值作为实际壁厚。
2 测量试验与讨论
为验证该测量方法的有效性,笔者采用多组工业CT图像进行实际几何元素测量,并与VG软件的测量结果进行比较,测量对象及其CT扫描参数如表1所示。试验程序运行平台分别为MATLAB 2017b和VG Studio Max 3.0。

表1 测量对象及其实际CT扫描参数
2.1 角度测量
第一组试验为角度测量,测量对象为精密光学零件,零件实物及其CT检测结果如图2所示。图2(b)中所标注的三处为待测角度,分别为45°,45°和90°,对应图中编号①,②,③,试验中采用锥束CT系统对精密光学零件进行部分扫描。为验证文中算法的稳定性,对该零件进行两次CT扫描,其结果如图3所示,图3(a),(b)分别为未加滤波片和加厚度为1 mm滤波片时的CT切片。由于滤波片可过滤一部分低能射线,降低射线硬化的影响,由图3(b)可看出,增加1 mm铜滤波片后图像的对比度和均匀性都得到了显著提升,有利于图像的分割和测量。

图2 精密光学零件实物及其CT检测结果

图3 光学精密零件CT扫描结果
对比试验中,采用VG软件角度测量工具进行四点式角度测量,调整4个的位置以实现多次测量,得到角度测量范围,其测量结果如图4所示,测量范围如表2所示。
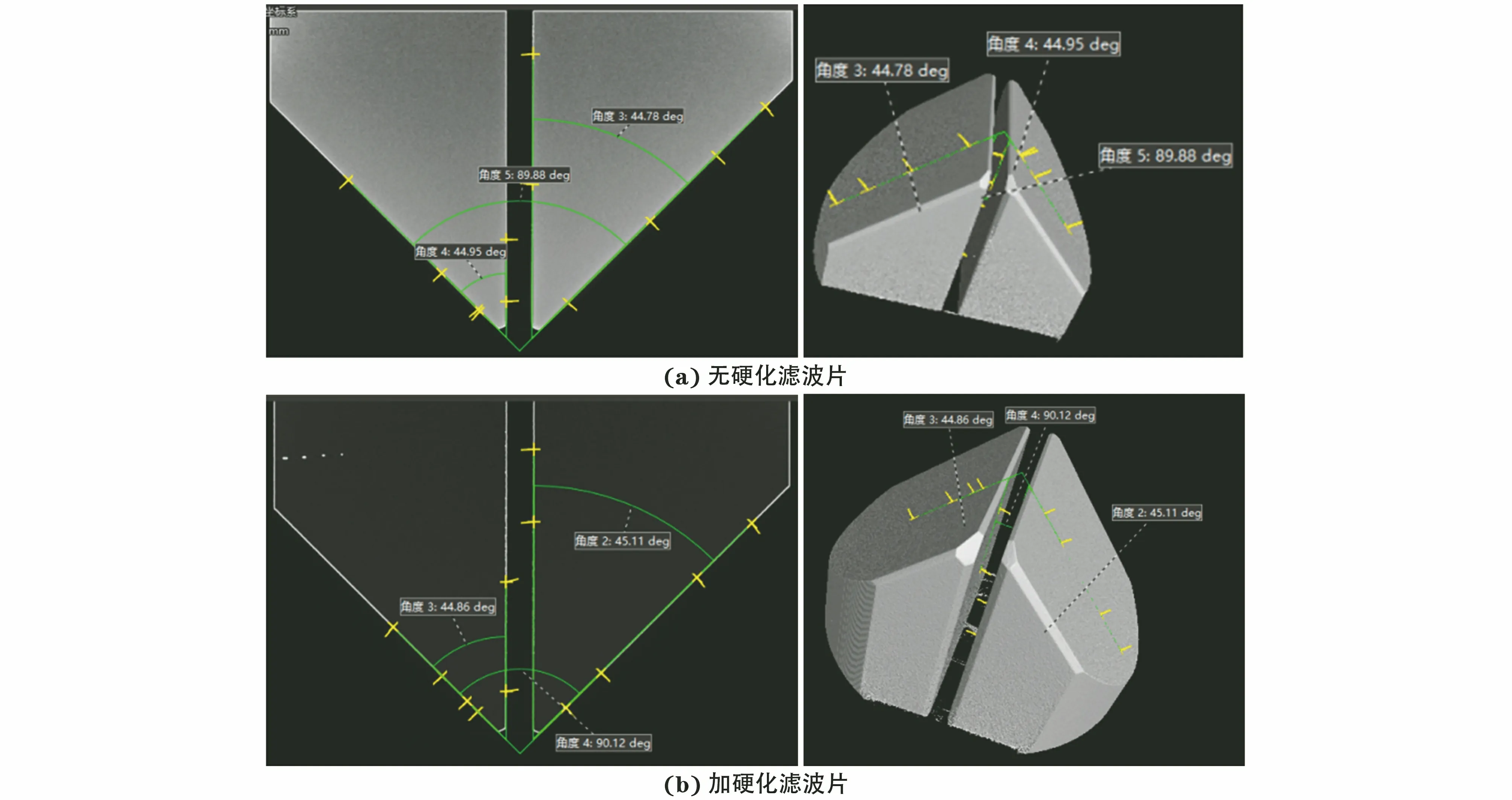
图4 VG软件角度测量结果

表2 VG软件角度测量范围
采用文中方法对精密光学零件的棱角进行测量,WT-RSF分割结果如图5所示。首先,通过WT-RSF方法分割得到光学零件的棱角轮廓(见图5中绿色线)。接着,分别提取棱角两边的轮廓点云,无滤波片和有滤波片条件下的角度拟合结果分别如图6,7所示;最后,根据最小二乘拟合原理,由棱角两边的轮廓数据得到棱角两条边直线方程,进一步由式(11)计算得到棱角角度,WT-RSF算法角度测量结果如表3所示。

图5 WT-RSF分割结果
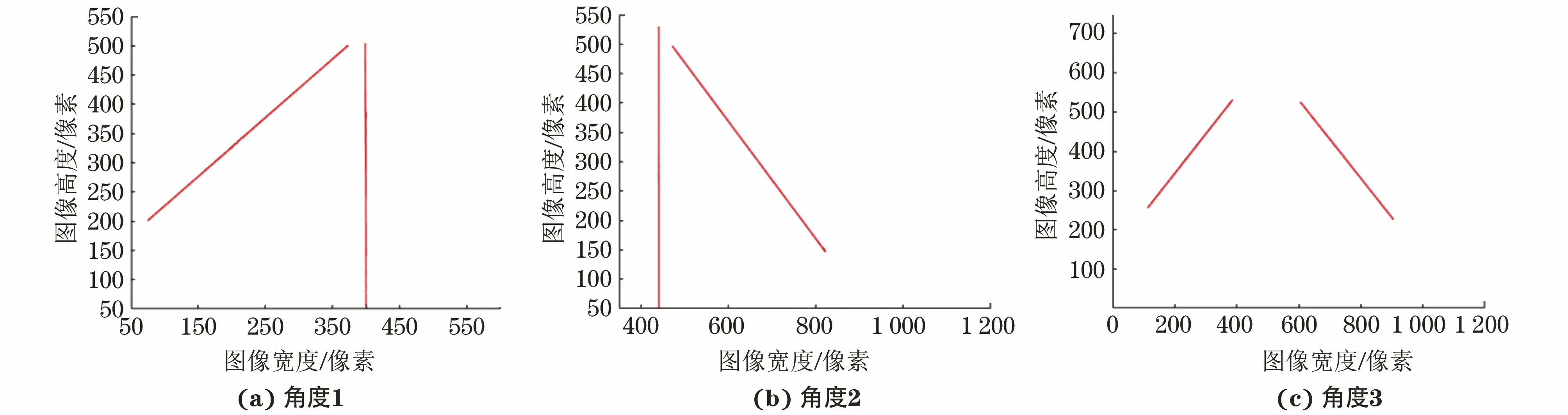
图6 无滤波片角度拟合结果

表3 WT-RSF算法角度测量结果
VG软件和WT-RSF算法角度测量误差对比如表4所示。由表4可以看出,未加滤波片时,由于受硬化伪影的影响,VG软件测量误差较大,而文中算法通过引入小波变换降低了干扰,测量误差相对较小;同时,当射线源前加1 mm厚的铜滤波片后,硬化伪影显著减少,有助于提升图像测量精度。即,相较VG软件测量结果,WT-RSF算法的角度测量误差总体较小。

图7 有滤波片角度拟合结果

表4 两种方法的角度测量误差对比
2.2 直径测量
第二组试验为直径测量,测量对象分别为一组圆柱试件和精密零件A(简称零件A)。其中圆柱试件组采用低能射线、线阵探测器CT设备进行扫描,零件A采用锥束微焦CT进行扫描,试件的CT三维图像如图8所示。图8(a)为直径分别为50,40,30,20,10 mm的圆柱试件组CT三维图像,分别标记为1#~5#;图8(b)为零件A的CT三维图像,其内部为空腔。试件的VG软件测量结果如图9所示。WT-RSF方法对圆柱试件组和零件A的CT图像分割结果如图10所示,分别提取分割图像中单个圆周各点的云数据,通过最小二乘拟合得到拟合圆的方程,进而得到待测圆的直径,不同零件拟合结果如图11所示。
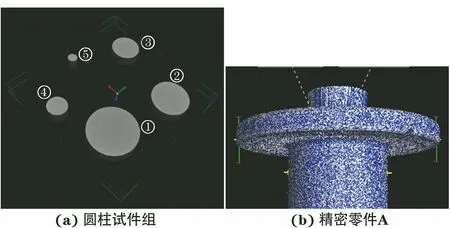
图8 试件的CT三维图像

图9 试件的VG软件测量结果

图10 WT-RSF方法分割结果
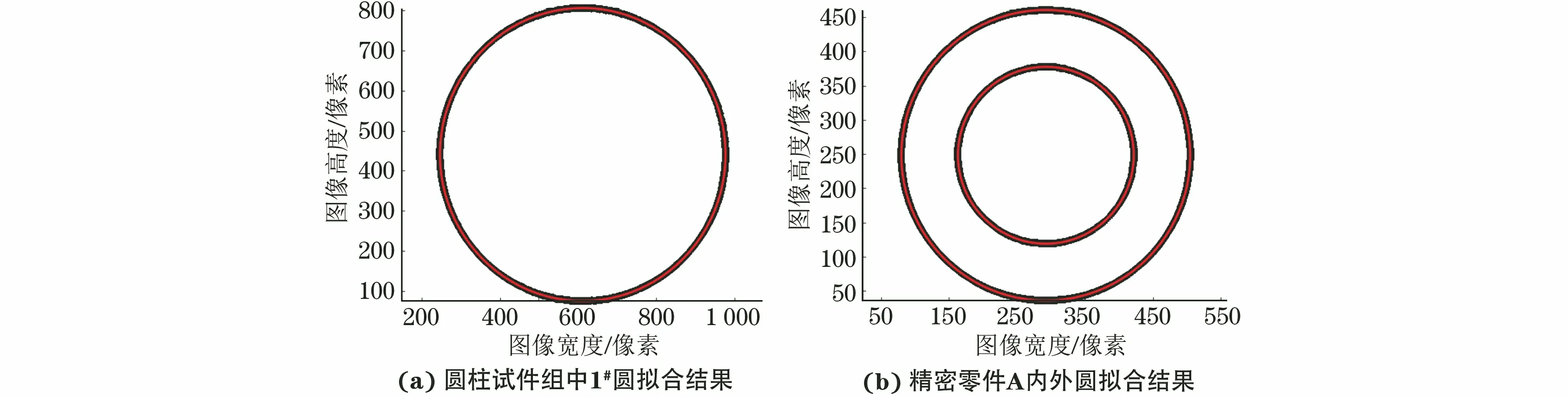
图11 不同零件拟合结果
不同试件不同算法下的直径测量结果对比如表5所示。由表5可以看出,VG软件和文中算法的测量误差均较小,但VG软件测量结果存在个别误差较大的情况。VG软件测量误差绝对值的均值为0.045 7 mm,标准差为0.043 7 mm;文中算法测量误差绝对值的均值为0.024 3 mm,标准差为0.016 8 mm。从整体上看,文中算法的测量误差更小、稳定性更好。

表5 不同试件不同算法下的直径测量结果对比 mm
2.3 壁厚测量
第三组试验为壁厚测量,测量对象为标准量块组件和精密零件B。其中,量块组件的量块依次排开并分别标号为1~9,其CT图像和WT-RSF分割图像如图12所示。量块组件厚度测量结果如表6所示。由表6可以看出,VG软件和文章算法测量误差基本为正值,这是系统几何放大倍数偏大所致。除10 mm厚量块测量误差较大外,文章算法测量精度略优于VG软件测量精度,达到工业CT测量指标要求。

图12 量块组件CT图像和WT-RSF分割图像
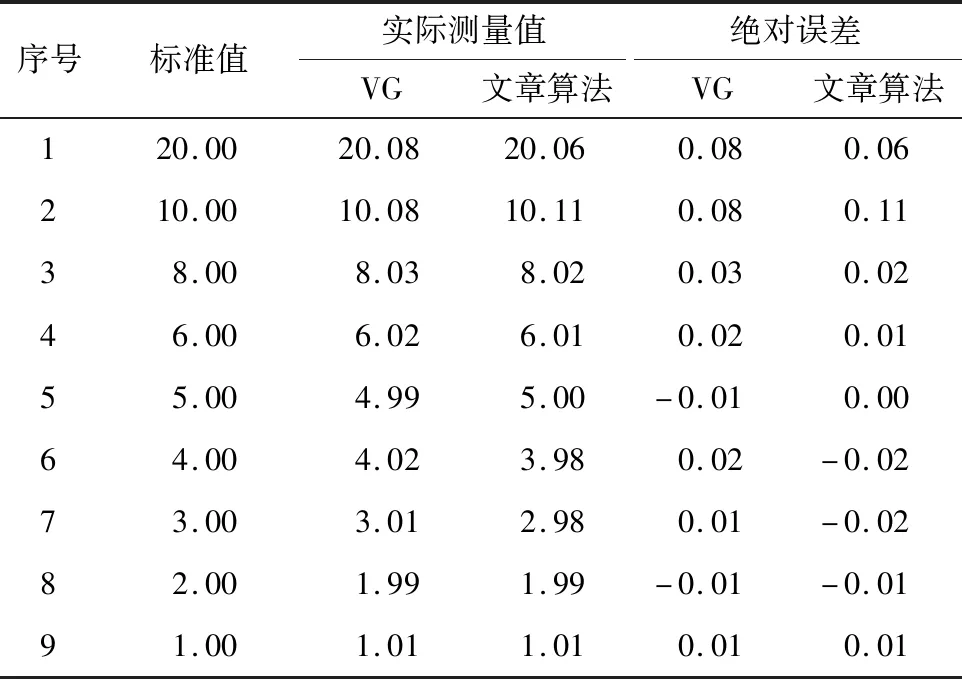
表6 量块组件厚度测量结果 mm
进一步采用具有空腔的精密零件B(简称零件B)检测壁厚测量误差。零件B检测图像如图13所示,微焦CT扫描三维图像如图13(a)所示,待测切片及其测量部位如图13(b)所示,WT-RSF方法分割图像如图13(c)所示。零件B不同方法测量结果对比如表7所示,包括采用千分尺、VG软件和文章方法的测量结果。若以千分尺测量值为真实值,由表7可看出,VG软件测量与文章算法测量精度相当。

表7 零件B不同方法的测量结果对比 mm
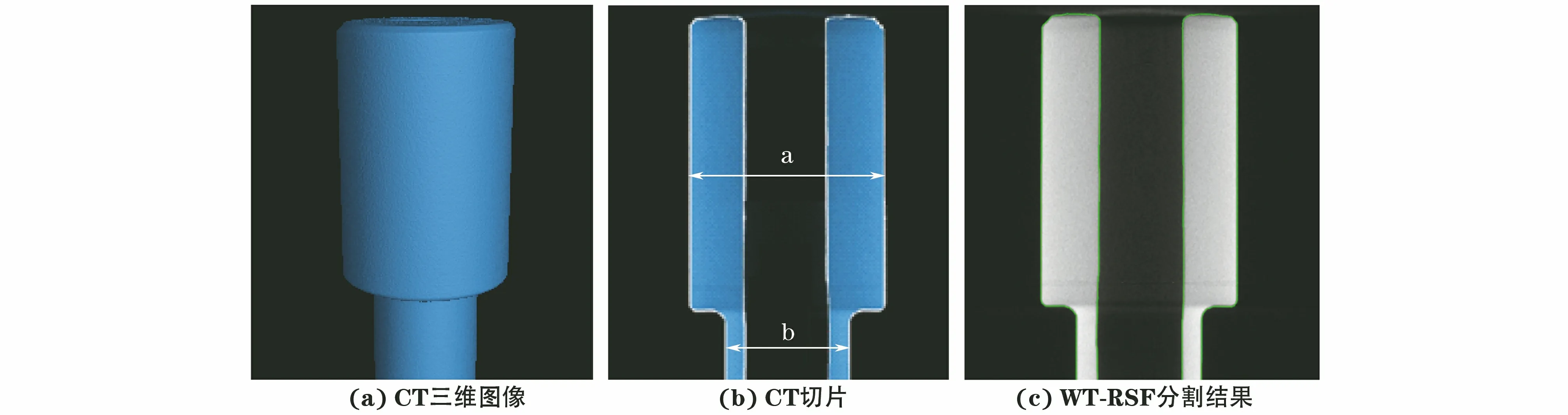
图13 精密零件B检测图像
可以看出,文章算法测量精度总体优于VG软件的精度。该算法不仅能提取到更精确的工件轮廓数据,且抗噪能力强,能满足实际工业CT检测中对精密零件的高精度测量需求。
3 结语
针对精密零件CT图像的精确分割和测量问题,提出了基于WT-RSF算法的图像分割方法,实现了直径、角度和壁厚等3种典型几何元素的测量,并与国际主流三维测量软件VG的测量误差进行对比。试验结果表明,该算法不仅能达到亚像素级的边缘定位精度,而且减少了射线硬化和射线散射伪影的影响,从而有效提高了CT图像测量精度,测量精度总体优于VG软件的精度,为相关软件的自主开发奠定了基础。
WT-RSF算法基于二维剖面或切片进行图像分割和拟合测量,后续研究工作需要将WT-RSF算法推广到三维CT图像分割,即由三维CT图像数据直接分割感兴趣区域轮廓,再进行三维拟合得到空间几何元素的测量值。同时,还需要进一步提高算法的运行效率,以满足精密零件CT图像的高效、高精度测量需求。

