基于VMD的相控阵超声信号降噪方法研究

俞燕萍，罗鹏斌，杨先明，郑 凯，胡斌定，王海涛

(1.江苏省特种设备安全监督检验研究院，南京 210036；2.南京航空航天大学 自动化学院，南京 210016；3.中国长城科技集团股份有限公司 中国长城研究院，北京 100083；4.南京华建检测技术有限公司，南京 210046)

0 引言

钢板作为钢材的主要产品之一，伴随着工业技术水平的飞速发展，如今在各行各业的应用十分广泛。不同厚度的钢板的应用场景也各有不同，中厚钢板作为航空航天、汽车、船舶、武器等高端且可靠性要求极高的产品原材料，钢板的质量直接决定了大型设备的整体质量和安全性。因此，在实际生产中对钢板的质量检测要求非常严格[1]。中厚钢板一般体积大，生产工艺链路复杂且耗时长，并且在实际应用中，常常会受到来自巨大冲击力和压力的威胁，加之还会受到温度、湿度、压强等诸多因素影响，导致其出现不同类型缺陷的概率大幅提高，如裂纹、夹杂、气孔等缺陷为钢板中常出现的几种缺陷，这些缺陷的出现不仅会影响钢板的使用寿命，而且若未能及时检测出，将带来严重的经济和人员损失。因此，为了加强钢板质量的可靠性，推动我国工业发展，保护生命安全以及财产安全，对钢板进行有效检测是重中之重[2]。

列车轮对是列车高速运行保障的重要部件之一，随着科技发展，轮对的健康状况直接关系到整部列车的安全，也是列车提速等相关研究的重要因素之一，列车在高速行驶过程中，车轮内部存在夹杂、车轮和轨道之间相互作用以及受到周围环境多变的影响，轮对极易出现内部缺陷，这对列车安全高速行驶带来了极大安全隐患，不仅会威胁到乘客的人身安全，还会带来巨大的经济损失[3]。因此，对列车轮对的健康状况的重视是关键，定期对轮对的全面检测，提高检测准确度是非常有必要的[4]。

作为无损检测中最常用的技术，超声检测基于超声波在接触不同介质时会产生反射和折射的原理，对有缺陷的试件缺陷检测时，可以利用超声波碰到缺陷界面反射波的信号来对缺陷信息做出判断。在超声传播方向上，声束指向性强，在同种材料中沿直线传播；在能量大小上，超声能量衰减较小，检测深度大并且穿透力强。综合来讲，超声检测过程成本低、检测精度高、易于便携，是工程检测的首选检测方式，在钢板质量检测领域具有重要工程价值。

目前，在钢板自动化检测中，常用方法为中心覆盖区域采用常规超声纵波直行希尔伯特变换检测，覆盖率达到一定要求即可，而板边缘的缺陷可能会产生漏检，板边检测常用的方法为常规超声纵波检测、相控阵超声检测技术[5-7]。在轮对检测中，常常通过人工超声检测，由于每天检测数量巨大，其检测效率极低，导致可能产生漏检。其中，相控阵检测技术检测精度高，效果直观，并且采用S扫，即同时可以拥有许多角度的超声波，等同于具有多种角度的探头同时进行检测，检测效率更高，故只需要沿着待检测钢板板边挪动，在实际生产过程中，具有极强的适用性。因此，展开基于相控阵超声的钢板板边和轮对内部缺陷定量检测研究。

超声回波信号既包含研究所需要的缺陷有效信息，也包含一些噪声信号，其中最常见的有电子白噪声，并且噪声在成像的研究和信号特征分析结果的好坏中起至关重要的作用，为了能得到可靠真实的信号，需要提高原始信号的信噪比，进而接着对信号进行时频域分析。常用的分析方法有小波包变换(WPT,wavelet packet tra-nsform)、希尔伯特-黄变换(HHT,hil-bert-huang transform)、集合经验模态分解(EEMD,ensem-ble empirical mode decomposition)、变分模态分解(VMD,variational mode decomposition)。以上方法各有特点，本质都是将原始信号按频率分解，得出频率随时间变化的情况，从分解后的信号中重构出有效信号来表征真实信号，提高信号信噪比。但是，他们分别存在小波基选择难，易发生模态混叠、自适应性差等缺点，然而，VMD是一种自适应、完全非递归的模态变分和信号处理的方法，对模态混叠、边界效应等具有很好的适应性，李宏坤等将模态个数和惩罚因子方法改为由中心频率和带宽自动确定，从而完成参数的确定[9-10]。蒋丽英等针对VMD中参数难以人为设定至合适值的缺点，提出了一种基于幅值谱的粒子群优化算法来对VMD方法中的参数进行优化，并得到了比人为确定参数更好的效果。因此，为了更全面的分析信号的特征，对信号进行时频域分析十分有必要。

VMD分解中参数的选择对分解的结果有非常重要的影响，K值选取较小，则会使分解略为粗糙，使得各分量无法精确重构表征原始信号，无法准确反映信号的整体信息;K值选取较大，则引起 VMD 的过度分解，使得分量信号与原始信号偏差较大。避免人为干扰，提出了一种参数寻优，自适应获取钢板和轮对散射信号的最优分解参数[11-14]。

综上，开展了基于瞬时频率均值优化的VMD算法相控阵超声内部孔缺陷与裂纹缺陷成像研究，来改善原始信号信噪比低的问题。

1 算法

1.1 变分模态分解

变分模态分解方法的本质上将一个实信号f(t)按照不同频率分解成K个子信号，通过对每个 IMF 的带宽进行计算，求解使模态带宽之和最小的变分约束方程。

1)变分方程的构造。

假设输入的实信号为f，f由有限个IMF模态相互叠加而成。每个固有模态都以某一固定的频率为中心，按照一定的带宽在其附近扰动。计算每个模态函数的带宽，最终找到带宽之和最小的K个模态。变分问题的限制条件是原始输入信号f的带宽与分解后各个带宽之和相等，具体的处理步骤如下：

①将所有模态函数进行希尔伯特变换，求取uk(t)的解析信号，就得到每个IMF分量

的单边频谱：

(1)

②将每个模态解函数的解析信号与预估中心频率进行混合，每个模态的频谱被调制到相应的基频带：

(2)

③计算调制后信号的梯度值L与L2的范数值，从而得到每个模态函数信号的带宽。加入限制条件后，受限制的变分问题方程变为：

(3)

{uk}={u1,…，uk}，{wk}={w1,…，wk}，

uk为中心频率，wk为瞬间频率，

2)变分方程的求解。

①在变分问题中引入惩罚因子α和拉格朗日乘法算子λ，引入这两个参数可以将分方程中的限制性问题变为非限制性问题。在信号存在高斯噪声的情况下，为了保证分解后信号的再次重构的精度，可以通过惩罚因子来判定，为了使约束条件更加严格，引入拉格朗日算子对其影响，引入后的拉格朗日方程变为：

(4)

uk最小化为：

(5)

wk最小化为：

(6)

VMD 算法流程：

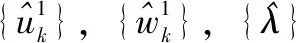
②根据公式5和式6更新uk和wk；

③更新λ；

(7)

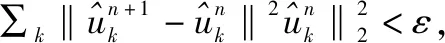
1.2 模态数K值的确定方法

根据VMD分解的基本原理可知，分解层数K的确定对信号的分解会造成较大影响，较小的K值将导致信号出现模态混叠现象，无法通过分量准确重构原始信号信息，较大的K值会使原始信号过度分解，此时每个分量信号与原始信号差距较大，各个频带范围窄，无法表征原始信号，而且运算量也会随着分解层数增多而显著提升。实际应用时通过反复尝试确定K值，根据实验所需要的频带宽度和中心频率来分析信号的特点，以此为依据来确定最优分解。针对上述问题，通过分析分量信号的瞬时频率均值曲线进而优化分解层数K。将信号分别以不同K值进行分解，K值范围选择由1取到9，分别绘制不同K值下的瞬时频率均值曲线，通过观察瞬时频率均值曲线变化规律来找到最佳的分解层数K。该优化方法思路是随着分解个数增多，信号会出现高频信号间断的情况，因此，尽管瞬时频率提高，瞬时频率均值反而会下降，瞬时频率均值会呈下降趋势；当K值较小时，瞬时频率均值曲线斜率较大且无过多斜率出现，表明此时信号分解中除了低频与高频部分，中间频带部分信息难以得到表现；当达到某一K值后，瞬时频率均值曲线以不同斜率下降且下降规律变化不明显，表明原始信号分解数过多，此时已达到最优层数K，因此，本文选择以瞬时频率均值曲线下降规律变化不明显时的K值为最优分解层数K。

因此，基于瞬时频率均值曲线的方法可以极大提高使用VMD分解时的效率，为使用VMD分解算法提供指导。

1.3 有效模态的选取

VMD 分解后得到的每个 IMF 分量中含有原始信号的特征信息不同，通常认为含有原始信号特征信息较多的分量可以表征原始信号的信息，与原始信号相关性较大，即为有效模态，反之，与原始信号相关性较小的分量由于不能表征信号信息，所含有的特征信息较少，即为噪声模态。通过选择实验所需的信号频带附近的IMF分量来表征原始信号，并比较各个模态与原始信号之间的均方根和信噪比，来评价筛选出的有效模态的可靠性，验证VMD算法的有效性，公式如下：

(8)

2 试验系统及实验结果

本次实验采用的是仪器型号为M2M的便携式超声相控阵设备,它是一款全集成64通道超声相控阵检测仪，可同时激发16孔径进行自发自收或一发一收检测[15]。本仪器最大数据传输速度为 10 MB/s，数字化频率为100 MHz，增益范围为 0～70 dB。采用了工程中常用的小尺寸探头，阵元数为16个，阵元间距是1 mm，中心频率为5 MHz，探头型号为 AXL-2.25 MHz，楔块型号为 AXL-55SW。

本次实验首先对材料为45号钢的轮对(如图1所示)，深度为15 mm处横通孔缺陷进行检测，后续对同材质的钢板(如图2所示)，深度为20 mm的裂纹缺陷进行检测，来验证该算法的可行性。

实验结果分析：

通过实验对钢板和轮对上缺陷处信号使用相控阵仪器进行信号采集，轮对15 mm深处横通孔缺陷信号与钢板20 mm深处裂纹缺陷信号以A扫描的形式显示，表现形式为检波信号。

将采集到的原始信号进行VMD分解后可以得到原始信号的相关的分量信号，接着将计算各个分量的瞬时频率均值，图3为钢板分解个数不同的情况下，个数分别为1～9时的各个信号瞬时频率的均值，图4为轮对分解个数分别为1～9的情况下的信号瞬时频率均值，横坐标为分解个数，纵坐标为当前分解个数下，信号各个分量的瞬时频率均值。

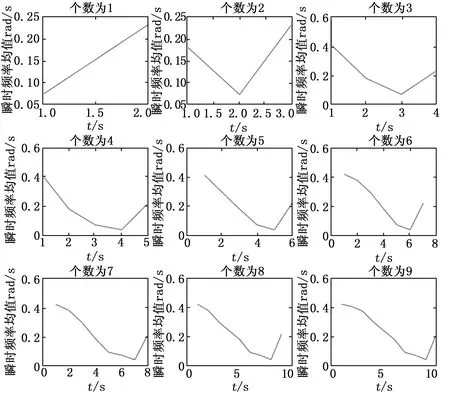
图3 轮对不同K值瞬时频率均值

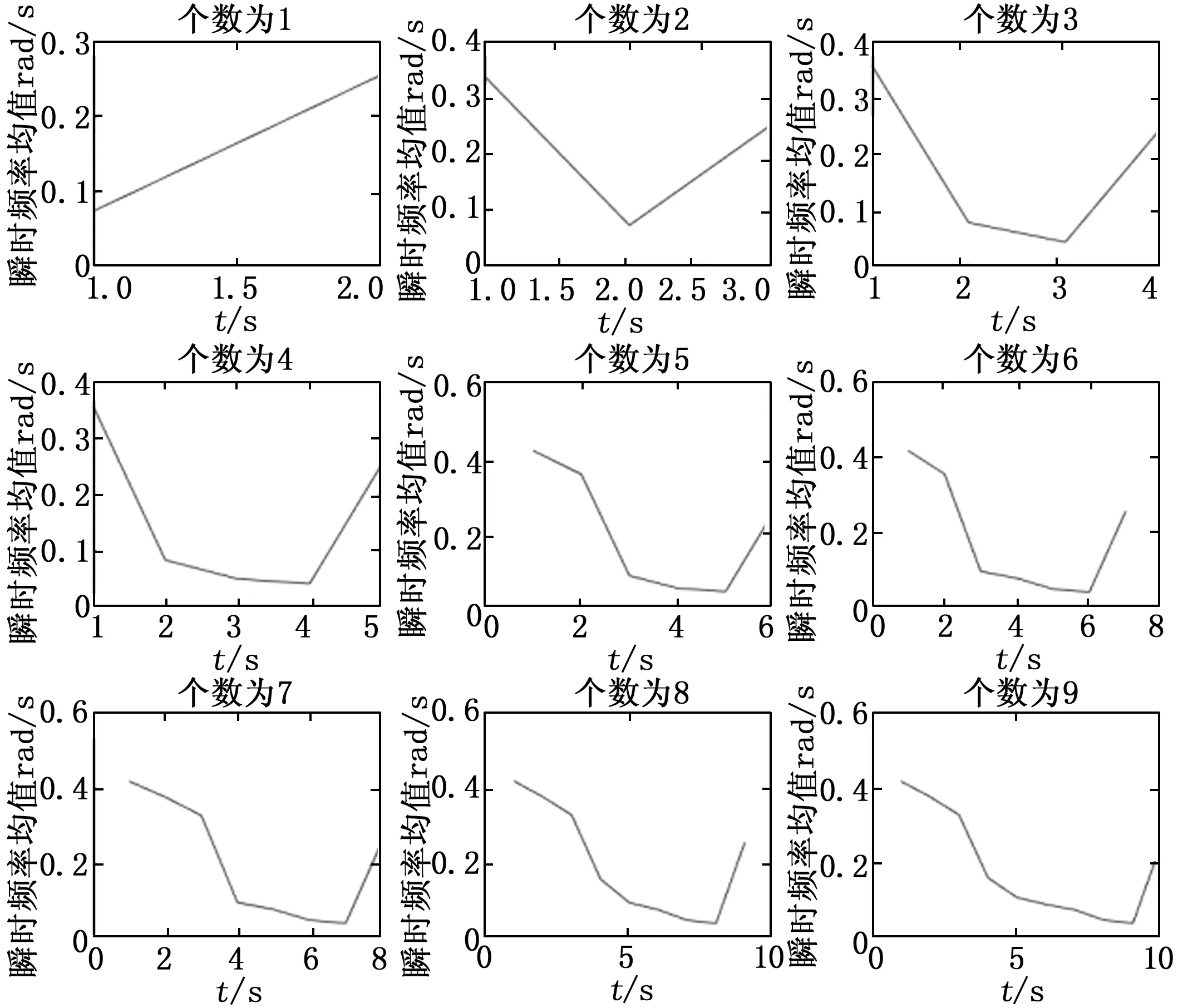
图4 钢板不同K值瞬时频率均值

观察图3和图4瞬时频率均值曲线特征，通过观察瞬时频率均值下降趋势，来分析K值的选择，随着分解分量个数提升，曲线整体呈下降趋势，表示原始信号因分解数量过大，高频部分开始陆续出现断断续续现象，导致瞬时频率均值下降。可以从图3中看出，轮对K值为1和2分解时，瞬时频率均值无下降趋势，说明分解个数较少，K值为3时首次出现下降，从0.4降至0.2，再由0.2降至0.1，说明此时分解不同频率的分量特征信息已经可以体现，但观察到K值为4时，会出现更多的斜率下降趋势，表明分解结果会更细致，故轮对信号分解时，本实验选择K值为4的分解。同理，钢板分解个数为1～4时，瞬时频率均值下降较快，从0.4降至0.1，说明此时分解个数不够导致中间部分的分量未能体现，只有低频和高频分量特征，在分解个数为5时，曲线首次下降至0.3～0.4之间后以不同斜率下降至0.1，此时说明更多频率分量在分解中都能体现。当分解个数K取大于5时，瞬时频率均值变化规律与K取5时基本一致，选取大于5的K值时对信号分解效果影响不大反而会极大增加计算量。从图中可以看出，首次出现非单一斜率下降的分解层数K为5，表示此时为临界分解层数，在实际实验中，可以通过在最佳临界K值和K-1的分解层数分别进行信号比较，通过分析实验所需信号所处的频带和分解结果，筛选出最佳K值，选择K值为4进行VMD分解。

在找到最佳分解层数K后，对缺陷信号进行相应K值的VMD分解，图5和图6分别为轮对原始信号K值为4的VMD分解和钢板原始信号K值为4分解后的结果，可以从图中看出分解过后将得到4个不同频率范围的分量IMF，从VMD分解的结果中分析得出，其中 IMF1与原始信号最相似，且IMF1分量的能量集中在0～5 MHz，与研究所需要的超声波纵波信号的频率一致。对比IMF分量与原始信号信噪比SNR和均方根误差，进而确定筛选出有效分量进行重构的可靠性。

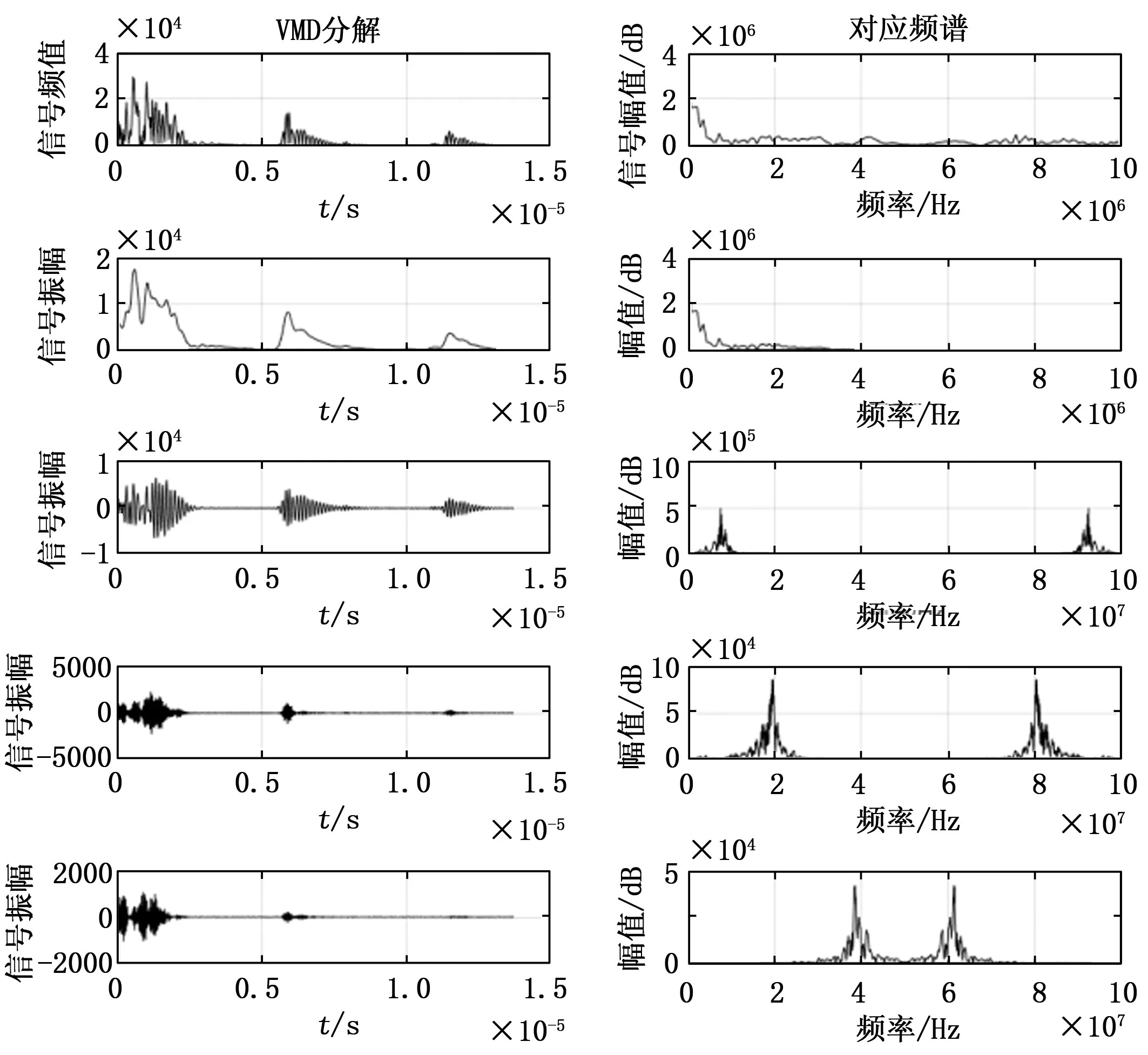
图5 轮对原始信号K值为4的VMD分解

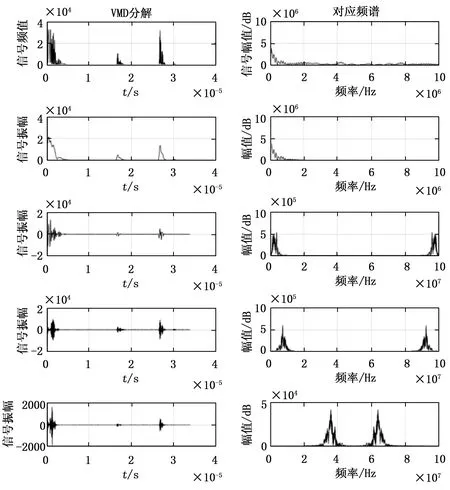
图6 钢板原始信号K值为4的VMD分解

通过计算各IMF分量与原始信号的信噪比和均方根误差，进而验证筛选出有效分量可靠性[14]。从VMD分解的结果可以直观的看出低频分量能很好地表征原始信号的整体特征，并且平滑性更好，接着通过分析原始信号与各个分量的均方根误差与信噪比，如表1～2所示，看出轮对横通孔缺陷信号分解后IMF1分量的信噪比相较于原始信号有显著提高，均方根误差表征信号的波动性大小，验证了分解后IMF1模态的有效性，故选取IMF1分量来表征原始信号用于后续成像研究。同理，表3，表4所示，看出钢板裂纹缺陷信号分解后的IMF1分量的信噪比相较于原始信号有显著提高，均方根误差也较小，同样验证了钢板裂纹缺陷信号分解后IMF1模态的有效性，故选取VMD分解后IMF1分量来表征原始信号。以此表征原始信号进行成像研究。根据公式(9)求出信噪比，其中，Asignal定义为回波信号的最大幅值，Anoise定义为图中局部噪声幅值的平均值，选取采集到信号中始波中一段信号取平均作为噪声信号，结果如表3、表4所示，可以看出IMF1分量信噪比比原始信号提高。

表1 轮对各个分量与原始信号比较

表2 轮对IMF1分量与原始信号信噪比比较 单位：dB

表3 钢板各个分量与原始信号比较

表4 钢板IMF1分量与原始信号信噪比比较 单位：dB

(9)

3 检测方法及检测信号分析

超声相控阵图像及信号分析：

对于钢板与轮对实验，通过上述瞬时频率均值选定VMD分解K值都为4，并通过比较分解后信号的信噪比以及均方根误差，选定IMF1分量为有效模态，对重构后的信号进行扇扫描成像(-30°- 30°),图7为轮对横通孔缺陷未经过处理的原始数据扇扫描图像，其中直径为2 mm埋藏深度为15 mm，可以看出轮对横通孔缺陷由于缺陷处散射信号信噪比低，扇扫描成像结果中有很多干扰波，很难清晰地看出缺陷的位置、形状及大小，能量也不够均匀。

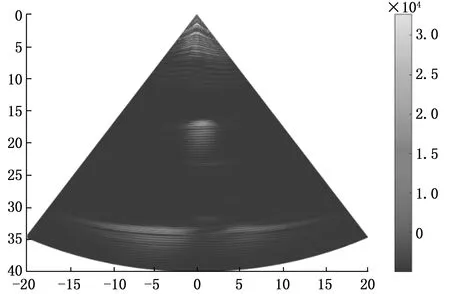
图7 轮对横通孔缺陷原始信号的扇扫成像

图9为钢板裂纹缺陷未经过处理的原始数据扇扫描图像，同样可以分析出裂纹缺陷成像的能量不均匀且不集中，有很多杂波干扰，对后续做缺陷定量以及缺陷特征提取有很大干扰；图8，图10分别为重构后轮对埋藏深度为15 mm横通孔缺陷和钢板中埋藏深度为20 mm的裂纹缺陷信号的扇扫描成像，可以清晰看出优化后的缺陷图像能量更加集中，并且杂波信号的影响基本消除，有效的解决了原始信号信噪比低的问题，通过观察结果，可以清楚定位到图中能量最大值点代表该缺陷的中心位置，方便后续缺陷定量分析。实验结果表明：VMD分解算法提高了原始信号的信噪比，有效的改善了钢板与轮对缺陷成像效果，为生产过程中缺陷的直观观察和精确定量分析提供了很大便利，同时也证明了使用有效模态表征原始信号的方法的有效性。

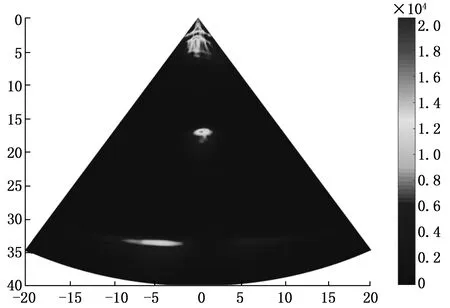
图8 VMD分解重构后的轮对横通孔缺陷扇扫成像

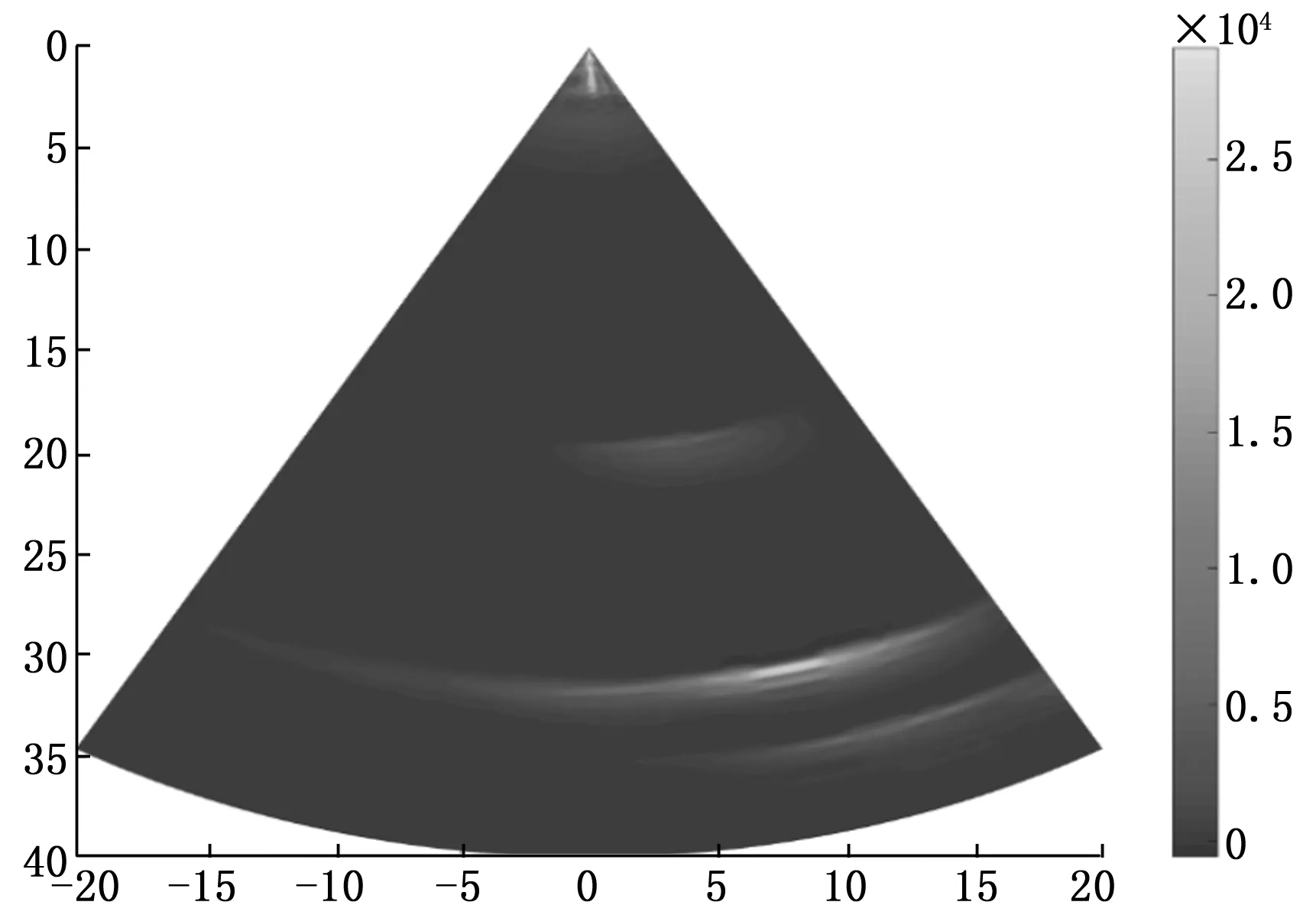
图9 钢板裂纹缺陷的原始信号扇扫成像

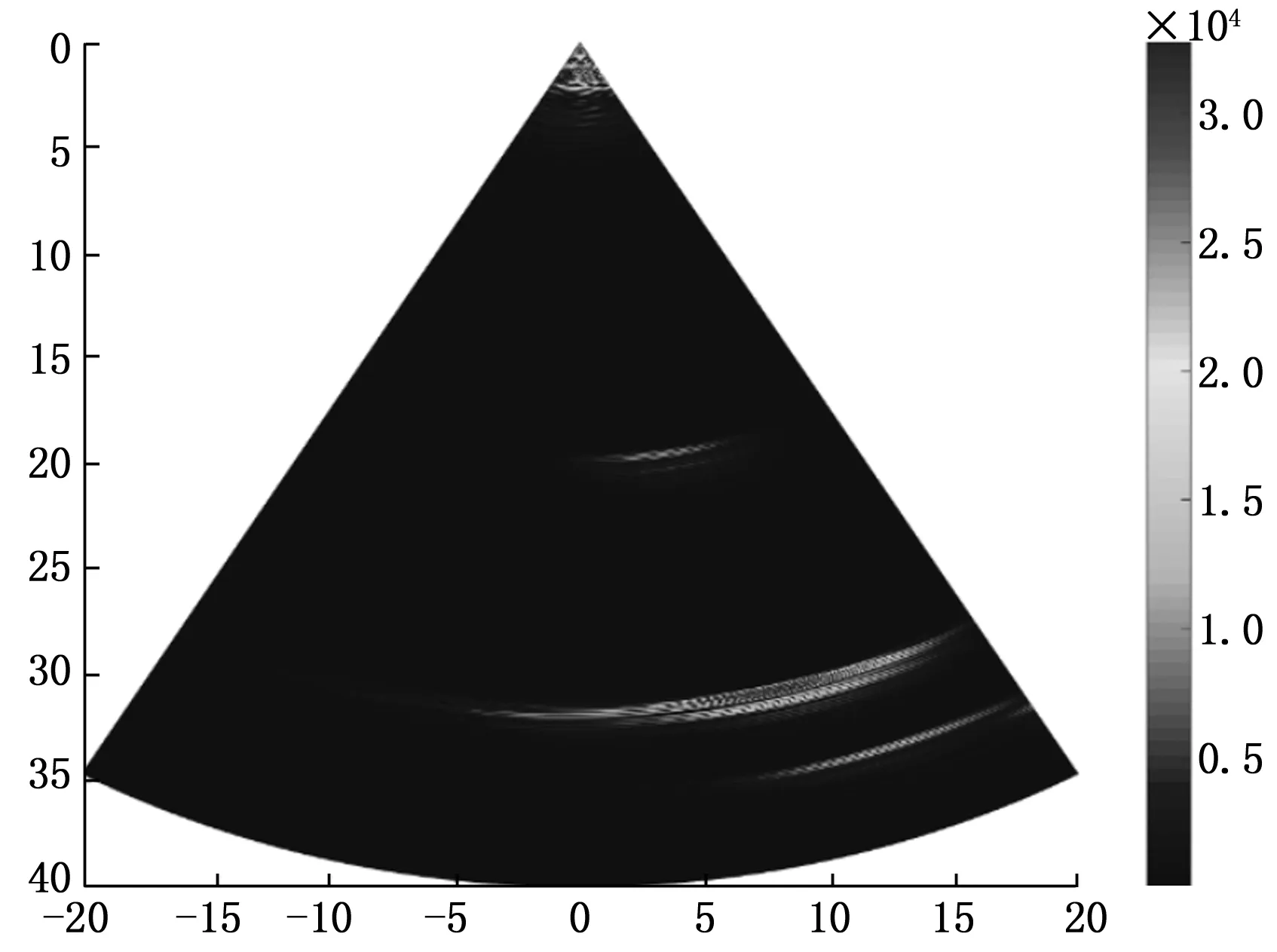
图10 VMD分解重构后钢板裂纹缺陷的扇扫成像

4 结束语

实验研究了相控阵超声对钢板裂纹缺陷和轮对横通孔缺陷检测，并提出一种有效的定位内部缺陷大小的方法，对深度为15 mm横通孔缺陷和20 mm裂纹缺陷进行检测，通过瞬间频率均值优化VMD算法，解决了传统VMD算法中存在的最佳分解层数K的选择问题，接着对采集到的检测区域超声纵波信号进行扇扫描成像。当对原始信号不做处理时，缺陷散射信号信噪比低的问题尤为明显，无法清晰定位及定量分析缺陷特征；对原始信号经过处理后，缺陷信号具有较好的保真度，信噪比与平滑度，较低的均方根误差，可以极大改善信号信噪比低的问题，清晰定位缺陷的位置及大小。综上，VMD分解算法可以提高信号信噪比，从而改善成像质量；结合分析信噪比与均方根误差，使用分解后分量表征原始信号特征的方法的可行性。为后期将对处理后的数据特征提取进一步进行缺陷识别奠定基础。