一种最小化安全多方计算任务的方法
姚友罡,肖 铮,2
(1.成都东软学院 保卫部,成都 611844;2.四川工商职业技术学院 信息工程系, 成都 611830)
0 引言
大数据分析是企业对外决策的关键环节之一,决策的数据往往来自不同的数据源。例如,从企业自身数据到城市数据、从基因数据到网络数据等,跨数据实体(数据源)分析是数据分析的迫切需求。然而,隐私数据或机密数据泄露已成为跨数据源分析的主要障碍,工业界、学术界致力于寻找跨数据源分析的实用技术。安全多方计算(MPC)作为一种密码技术,允许独立的参与方在不泄露自身私有输入的情况下联合执行所需的计算,是跨数据源分析的常用技术之一。自20世纪70年代末提出MPC概念[1-3],到如今的30多年历史里,一直是密码学研究的活跃领域。近年来,MPC的研究取得了重大进展[4-6],然而,由于以下四方面的原因,使得MPC的研究仍局限于概念验证阶段[7]:
1)因涉及密码学相关技术,MPC应用、部署较难。
2)MPC无法利用现有的成熟算法,需要从头开始部署。
3)现有的MPC引擎是孤立设计的,不适应如MapReduce之类的云编程范式。
4)MPC开发所需的编程/工程专业知识异于在敏感数据集上评估隐私泄露所需的专业知识。
与专注于MPC协议原语的实现不同,从MPC技术在云计算环境中的实际应用与企业项目开发角度考虑如何处理这些问题,即将MPC集成到云计算的编程范式中。更具体地说,同时扩展了MPC的MapReduce实现技术,允许多方利用自己的计算资源,支持多方计算(MPC)和MapReduce的混合编程。本文的创新点和主要贡献如下:
首先构建了MPC最小化的基本思想及实现步骤;其次,以线性聚类为例,提出了一种在确保安全性的同时最小化MPC实用计算的方法。该方法允许将计算划分为MPC计算部分和非MPC计算部分,其中非MPC计算部分在本地簇完成,无需多方通信,可并发执行,从而提高计算效率。最后,本文构建了一个实验原型系统,并以UCI数据集为例,验证了提出技术的可行性与正确性。
基于以上目标,全文的结构安排为。第1节讨论了大数据相关技术,特别是MapReduce编程基础,常用的MPC实现技术以及MPC与非MPC相关的划分技术。本文的技术创新性工作在第2节中展示,以线性聚类为例,分析MPC与非MPC划分方法及与MapReduce混合编程技术。第3节展示了以UCI机器学习数据集为基础的实验及实验结果数据。最后,第5节为结论以及对下一步工作的展望。
1 相关工作
文中主要讨论提高MPC计算效率的技术与方法,即如何有效地将MPC技术融入大数据处理流程,不涉及MPC协议原语的实现或大数据处理等技术问题。与本文相关的工作包括Pyspark数据分析技术、MPC技术以及提高MPC运行效率的现有方法与实践等。
1.1 Pyspark数据分析技术
Pyspark源自Apache的Spark项目,是为实现用Python语言编写Spark应用程序而对Spark的封装。作为Hadoop中MapReduce的改进与替代方案,Spark引入了弹性分布式数据集(RDD, Resilient Distributed Datasets)这一基于内存的数据结构,以适应交互式、实时、分布式与容错的低延时应用。Spark使应用开发人员专心于业务逻辑的开发而无需担心基础架构、环境等问题。文中利用Spark的并行处理能力,提高非MPC类计算的效率(完成的主要计算任务是矩阵乘法,该部分的内容在2.3节)。
1.2 MPC技术
安全多方计算作为一种通用的加密原语,在保护个人或组织数据隐私的同时实现多方私有数据的分析与挖掘。常借助电路 (布尔电路或算术电路)的概念以建立MPC的形式化定义。通用的安全多方计算的定义如定义1所示。
定义1:安全多方计算
在n个互不信任的参与方之间的安全多方计算(函数)F,常用是一个三元组来表示:
F=(C,Ti,To}
(1)
其中:C表示电路,是用户需求、功能、算法的抽象;Ti表示输入方及其输入数据的集合;To表示输出方及其输出数据的集合。在F的计算过程中,要求任意参与方pi除获得自身的输出信息外,均不能获得其他参与方的任何输入或输出信息。MPC的这一定义是较为严格的,实际应用中往往放宽某些限制,以提高效率。
已有一些基本子协议(技术)用于构建MPC协议:这些子协议(技术)主要包括:1)不经意传输(OT,oblivious transfer)协议;2)加密电路(GC,garbled circuit)技术;3)同态加密(HE,homomorphic encryption)技术以及秘密共(SS,secret sharing)协议。从这些基础协议构建MPC实用程序不是易事,需要了解密码学的相关知识。目前业界已提出MPC的实可编程式现框架,这些框架主要包括Obliv-C、ObliVM、SPDZ、Sharemind等。在实际应用中,借助于技术实现框架,即便是不具备密码学专业知识的应用程序开发人员也能编写实现数据安全分析的任务。另一方面,虽然这些框架都是基于MPC技术独立实现的,但各自拥有不同的特性及优缺点。因ObliVM及SPDZ不再维护或更新,本文的实验部分,采用了Obliv-c及Sharemind的作为MPC的评估版。为此,表1列出了这两种框架的特点差异。
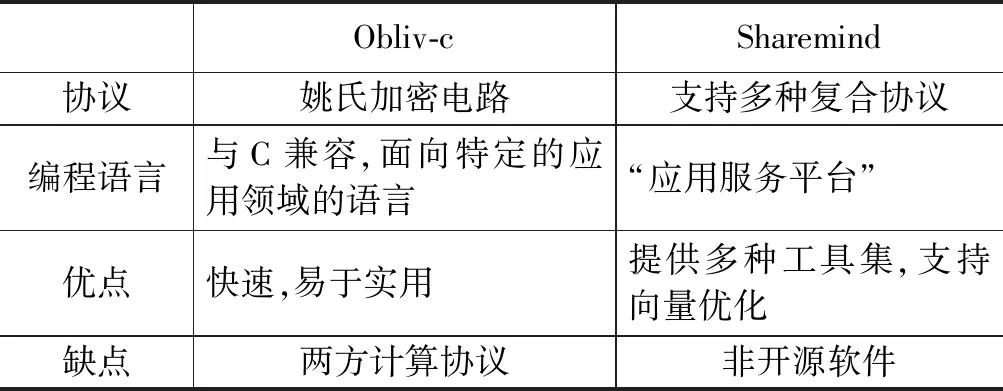
表1 常用MPC实现框架特点对比
1.3 现有方法
在本小节中,先后简要描述了加速MPC计算的方法,以提高多方计算高效可行。目前,有两种互补的提高MPC计算效率的方法。其一是直接提高MPC计算协议并发度;其二采用混合MPC计算。前者从MPC协议角度出发,通过并发实现茫然计算。这种对MPC效率的改进有限,特别是不适应大数据处理需求。后者将安全计算按照一定的规则划分为不安全的非MPC类计算及少量的安全MPC类计算,通过提高非MPC类计算的效率间接提高计算的整体效率。两种方式都基于到MapReduce编程范式的基本思想,文中着眼于第二种实现方式。
文献[9-10]先后提出并证明“并行有助于不经意”以及流式MapReduce的概念以及任何在流式MapReduce抽象中编写的程序都可以被转换为高效的不经意的算法,并利用这一想法涉及了网络ORAM方案。Liu等人[11]等人则基于MapReduce编程抽象构建MPC实现框架,即ObliVM 同年,Kartik等[4]设计并实现的GraphSC框架都属于提高MPC计算协议并发度的范畴。
Rastogi[12]等首先提出了混合MPC计算方法,其中非MPC的计算,各参与方在本地独立完成作业,类似普通的应用程序。MPC计算部分由各参与方协同,共同完成。然而,在Rastogi等人的设计中,需要程序设计人员手动标注非MPC类及MPC类计算。虽然这些标注是精细化的,但程序设计人员需要具备专业的MPC知识,使其应用受到限制。在此基础上,文献[12]进一步将MapReduce编程范式融入到本地非MPC计算中。在他们的设计中,参与计算的节点可以分为两种类型:控制节点和工作节点。其中,控制器节点作为任务分配器、作业监督器以及任务同步器并作为节点间共享公共数据的存储介质;工作节点跨参与方完成MPC任务,如访问参与方自身的私有数据,充当本地MapReduce任务的执行器。文献[14-15]借助有向无环图(DAG)研究与查询相关的MPC计算及其可扩展性问题。与上述工作不同,文中以线性回归问题及其扩展为主要研究目标。
2 实现方法
本节首先介绍了最小化安全多方计算的基本思想及步骤,然后以线性回归模型为例具体讨论相关技术及方法。
2.1 基本思想及步骤
本文提出的最小化安全多方计算(下文常称为计算)的基本思想是使MPC类的计算尽可能少,只实现必要的MPC,即能不用MPC实现的尽可能不采用。如何能最小化MPC类的计算,本文提出将计算分解、转换为有向图,进而简化MPC,重构MPC算法。步骤总结如下:
1)确定数据的属主。根据算法所属数据属主的差异,确定数据的“主人”。
2)确定信任标注(可选)。根据数据属主,确定参与者之间的信任关系。这种信任关系可能繁殖,或者终止,这些工作采用自动以及交互的方式来实现。
3)算法重写。即获得与当前算法等效的算法,但其需要的MPC类计算更少。区分本地计算以及多方计算等;采用的技术包括信任繁衍、组合、分割。
4)MPC优化。MPC优化技术包括:MPC前端(MPC操作与本地明文操作之间的边界)下移、MPC前端上移以及混合操作(如混合联接、公共联接和混合聚合)等。
5)算法优化。除了对单个计算节点的优化,算法的整体性能也应优化。常用的方法是减少对MPC底层算法的依赖。
本节的余下部分以线性回归预测模型为例,讨论最小化MPC计算的实现方法。
2.2 线性回归模型
线性回归预测模型是一种有监督的学习算法,是许多机器学习算法的基本组成部分。它通过拟合训练数据集的线性曲线来获得目标模型并实现预测,该模型的通用公式如式(2)所示。
Y=Xθ+ε
(2)
式中,Y∈Rn,是由n个元素的列向量组成的目标变量,也称为标签或因变量;X∈Rn×d,是n行d维的输入向量,即因变量;θ∈Rn,称为拟合参数或模型参数,ε是为了平衡模型两边的值而添加的部分,称为误差项。
求解方程(1)中的模型参数的过程称为模型的学习,常通过最小化均方误差来求解,如式(3)所示。
(3)
式(3)称为线性回归的目标函数。更一般地,线性回归模型的目标函数可写为如式(4)所示。
(4)
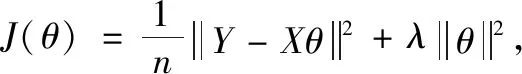
首先展开平方项得等待如下的式子:
(5)
式(5)对θ的一阶偏导数为:
(6)
在式(6)中,令导数等于0,可知回归系数满足式(7):
(7)
如第1节所述,提高大数据分析的安全计算效率的基本思路是,尽量降低MPC类计算的需求,为此文中采用如下两阶段的优化措施。
2.3 数据计算优化
该阶段从计算的内在需求出发,找出MPC类计算与非MPC类计算部分。为计算式(7)需考虑两种不同的数据分布情况:1)数据在参与方间水平分割,即一个参与者有一条完美的;2)数据在参与方间垂直分割。
2.3.1 数据水平分割
该阶段从计算的内在需求出发,找出MPC类计算与非MPC类计算部分。为计算式(7)需考虑两种不同的数据分布情况:1)数据在参与方之间水平分割;2)数据在参与方之间垂直分割。
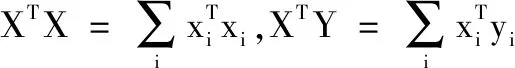
2.3.2 数据垂直分割
在垂直分割下,数据X按属性划分,并由各参与方持有。即X=[x1,x2,...,xi],xi∈Rn×β(β⊆d)由参与方i持有。特别地,考虑两方参与的情况,即数据X被划分成X1,X2两个子集,并分别由参与方p1和p2方持有。变量Y由其中一方持有,这里假设Y由p2持有。则式(7)中的因子XTX可以用式(8)表示:
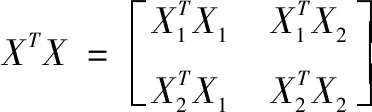
(8)
XTY的结果如式(9)所示:

(9)
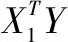
2.4 计算流程优化
该阶段从计算需求出发,使用DAG (Directed Acyclic Graph)图来表示计算流程,并利用DAG图的内在联系,进一步降低MPC类的计算需求。在利用共轭梯度下降法求解式(7)的解时,参考文献[8]可得如算法1所示求解思路。
使用DAG图表示程序流程及模板的通用性,如图1(a)所示。图中圆形内的阿拉伯数字对应算法1中的序号,圆形旁的字符是参与方的缩写。
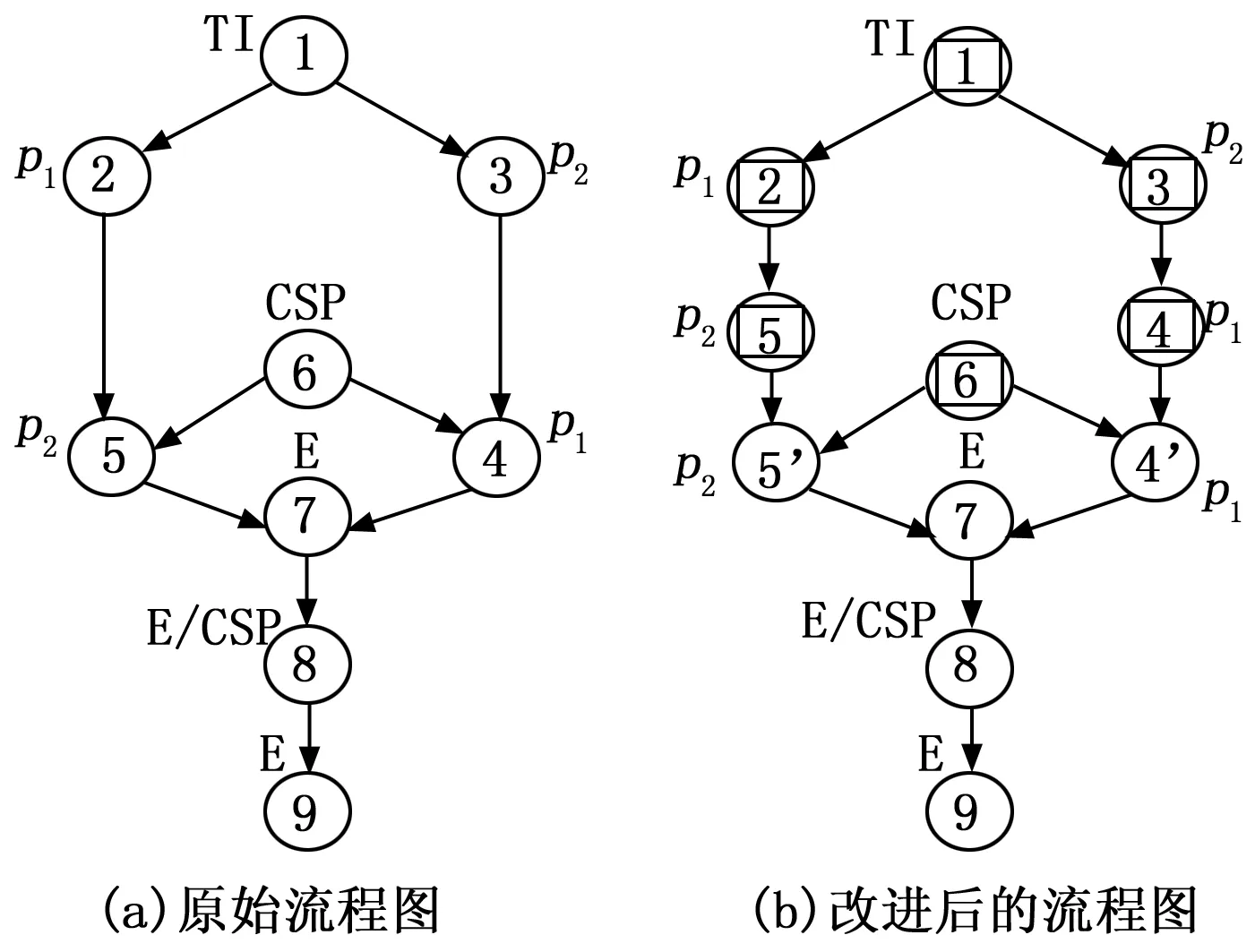
图1 安全计算流程及其改进措施
算法1:优化的安全多方(以两方为例)计算求解算法
参与方:数据提供者p1、p2,可信初始值设定者TI/加密服务提供商CSP、电路评估者evaluator
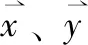
输出:数据提供者共同学习到的模型参数θ
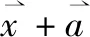
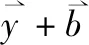
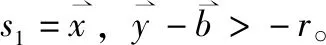
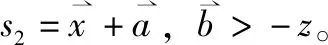
6)CSP生成重构及求解式(6)的混淆电路C ,并将其发送给评估者evaluator。
7)数据提供者与加密服务提供商CSP之间利用茫然传输协议获取其在混淆电路C中的共享输入,并将该共享值转发给电路评估者evaluator。
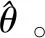
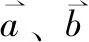
对于处理的数据,为提高安全计算的效率,增加三方面的额外信息:1) 增加计算数据所有者域及数据所有者传递规则(某计算节点的数据所有者域由该节点的数据提供者及其输入弧传递进来的数据所有者共同确定,数据所有者沿图结构向下传递,受信任标识集的影响而可能终止)。2) 增加计算结果数据的接收者域(由弧的终点确定)。3) 增加数据安全处理需求,用于表示该数据是否需要在MPC下完成计算。例如,图1(a)中,计算节点①的没有输入弧(入度为0),即该节点没有输入数据,其数据所有者域仅包含该节点自身,即可信初始值设定者TI。该节点有两条输出弧(出度为2),表示该节点有两条输出信息,其接收者分别是两条弧指向的节点,即数据提供方p1和p2。同时该节点数据不包含隐私信息,仅需通过安全通道传递给接收方即可,可见针对该节点的计算无需在MPC下执行。
增加数据信任标识集,即由数据提供者授权的可在明文状态下(非MPC计算类)使用其数据的使用方构成的集合。例如公共数据或多方共享数据的所有者构成了这些数据的信任标识集,同时信任标识集也可以是权威数据管理机构,他们拥有参与方的原始数据。信任标识集里的各参与方在明文状态下使用数据,降低了计算成本。
节点分裂与繁殖,即将复杂的MPC类计算节点细分成MPC类计算节点与非MPC类计算节点。目前,存在3种方式实现节点分裂与繁殖。其一是利用上述两项措施,即当节点计算执行参与方是节点计算数据的所有者或者执行方属于节点数据的信任标识集,该类计算可以划分为非MPC类计算。其二是通过添加混合协议,即将部分高负载的MPC类计算在可信方完成,从而分离出非MPC计算类与轻负载的MPC计算类,其三是利用数据已有计算结果及数据混淆技术减少计算茫然性的需求。节点分裂与繁殖进一步减轻了MPC计算负载。
图1(a)的DAG图,在经过上述处理后步骤后的DAG图如图1(b)所示。其中带方框的节点属于非MPC计算类。从中可以看出MPC安全计算结点的数量有所降低。
3 实验与评估
3.1 实验设置
本节建立了以Python编程语言为基础的实验开发环境。为突出实验效果,实验共设置了4个参与节点,各节点都配置有4核CPU(2.4G)以及8G的内存。其中2个作为数据提供者;一个作为可信初始值设定者TI及加密服务提供商;另一个作为数据评估者。各参与节点都配备有本地Pyspark组件、MPC组件、私有数据访问与存储接口以及用于与控制器节点通信的网络接口。其中,评估节点以及两个数据提供者节点组成了含3节点的Spark独立集群。评估节点作为Spark的主节点,数据提供者节点是Spark的工作者节点。MPC组件的实现采用的是Obliv-c,通过Python的模板替换工具Pystache,以及算法流程的DAG图自动生成MPC与非MPC代码。评估用的数据集来自UCI机器学习数据集,数据集及其主要特性如表2所示。各数据集按7∶3的比例随机选取作为训练数据集与测试数据集,并将数据按1∶1的比例随机分配给数据提供者p1和p2。
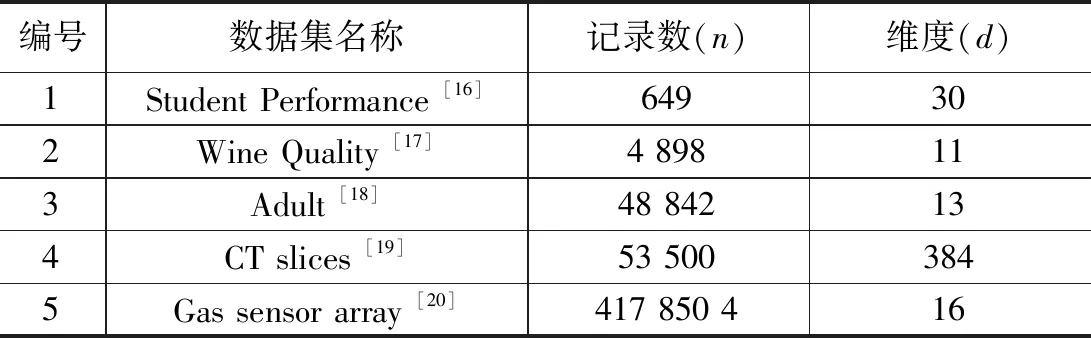
表2 实验数据集及其主要特性
基于以上的实验设置,主要完成了以下两方面的评估指标。
运行时间:针对不同数据集,在不同MPC优化层次下(包括在Pyspark下的全明文技术)运行时间不同的优化参数对MPC运行时间的影响。
预测精度:即在各种设置下所获得的预测值与真实值之间的根均方误差(RMSE)。
3.2 实验评估
本节从运行时间及精度两方面讨论算法的性能。
3.2.1 运行时间
针对不同的数据集,在相同的设置(如3.1节所述)不同的安全配置(全明文Pyspark、现有安全多方计算Obliv-c以及文中的优化设置)下,各重复实验10次,记录其平均值,实验结果如表3所示。
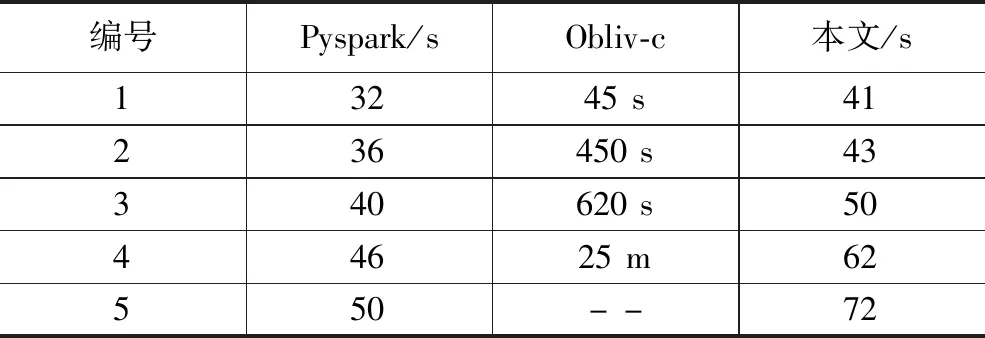
表3 不同设置下各数据集所需运行时间
实验结果表明,所有不同的安全配置下运行时间都随记录数的增加而增加,同时运行时间也受数据维度的影响。总体而言,全明文分析所需的时间最少,现有安全多方计算(Obliv-c)所需时间最多,本文提出的方法与全明文分析所需时间十分接近。另外,可以注意到当记录数达到万级以上时,Obliv-c的运行耗时迅速增加,如本例中的CT slices数据集,其运行时间在25分钟。当记录数继续增加时,该方案甚至不可接受,如本例的Gas sensor数据集。可见文中提出的方法显著降提高了运行效率,提高了应用在时间的可行性。接下来分析该方案在精度上能否满足要求。
3.2.2 精度
与3.2.1节运行时间设置相同,同时记录了现有安全多方计算Obliv-c以及文中的优化设置两种情况下的根均方误差,如表4所示。
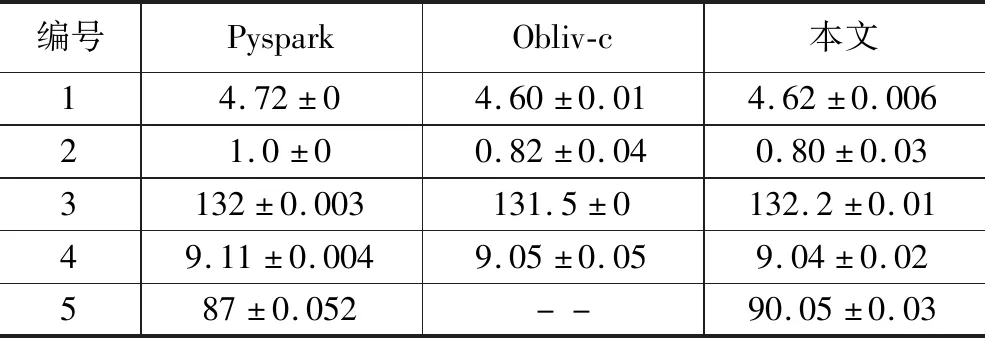
表4 不同设置下各数据集的根均方误差
可见,各种方法在精度上的差异并不显著,3种安全配置下的根均方误差大致相同,即文中设计的方法(在现有技术条件下)满足精度需要。
4 结束语
本文以数据分析中的常用方法——线性回归为例讨论在安全多方计算中如何提高数据分析的效率。提出的优化措施包括:计算优化以及执行流程优化。在实验部分,针对UCI真实数据集完成的实验验证。实验结果表明,文中提出的方案在精度、时间上都是可行的。下一步准备将混合MPC以及MPC并行化相结合,进一步验证文中提出的方法的可行性。另一方面,如何将混合MPC技术推广,以适应更多的真实应用场景也是未来工作方向之一。同时如何减少对可信初始值设定者、加密服务提供商、电路评估者的信任和依赖,从而提高系统可信性,也是未来应考虑的主要工作之一。以去信任为中心的区块链技术提供了相应的解决思路。

