基于响应曲面法的某转向桥减振器支架结构设计

王帅，王凯,吕兆阳，梅峰，王栋梁

安联(郑州)工程机械有限公司，河南郑州 450001

0 引言

在工程实际中经常会遇到安装位置可调整部件的零件设计工作，对于该类零件设计时需要考虑诸多因素，如结构尺寸、安装空间、调整范围以及区域内的力学性能等。通常情况下，设计师可依靠设计经验确定简单零部件的结构及材料参数，而对于复杂、多适应性的零件则需要综合考量上述因素开展设计工作。这就需要在设计时恰当地运用一些试验设计方法来提升设计效率，改善设计结果。

本文采用响应曲面法对一款转向车桥的减振器支架进行了结构参数设计选择，获得了该支架工作强度Von Mises应力与其板材厚度、减振器安装孔位竖直及水平方向尺寸等3个因素的关系方程式，并利用SolidWorks软件分析验证了上述方程式的精确性，最终取得了很好的效果，同时为后期同类产品以及系列产品的研发工作提供了参考和便捷。

1 工程问题描述

图1为某款在研转向桥产品。该款车桥为盘式自转向车桥，转向驱动油缸安装在轴管的两个油缸支架上；受限于车桥自身尺寸及其使用空间，减振器一端通过抱箍支架与车桥转动侧连接，另一端需与车桥固定侧连接(图中安装在油缸支架之间的减振器支架，即文中研究对象)。车桥转向动作时，油缸活塞杆动作，可推动车轮左右旋转，而减振器作为阻尼缓冲件可减少冲击和振动。

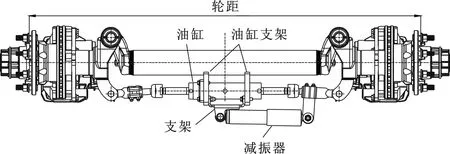
图1 某款在研转向桥产品

此外，车桥产品根据轮距不同，便可形成系列化产品。由图1可知，通过设计不同的减振器支架或者调整抱箍支架安装位置，便可实现减振器安装位置的调整以适应不同轮距的车桥产品。因此，有必要对该款车桥的减振器安装支架进行设计分析，以期获得既满足实际功能使用要求，同时又具有较大适用范围的支架设计方案。

2 试验设计及分析

2.1 试验方法及设计参数选择

2.1.1 试验方法选择

在工程应用中常用的试验设计方法有很多，文中针对减振器支架结构参数进行相关试验设计，从而获得选定因素的表达式关系，进而指导实际工程工作。对比多种方法后，选择采用响应曲面法进行相关设计。

响应曲面法是通过合理设计试验方案并利用仿真或试验获得一组数据，然后采用回归分析的方法以及最小二乘法原理来拟合存在于设计因素与设定响应目标间的函数关系，最后获得回归方程并通过对其分析以寻找最佳设计参数，从而达到解决多变量优化问题的一种统计学方法。RSM最初由英国知名统计学家GEORGE和WILSON于1951年提出，并已广泛应用于生物、电子、化工、机械、农业等领域中，成为工程实际中寻求最优方案的有效手段和工具。

2.1.2 设计参数确定

减振器支架主要涉及强度问题，而与支架强度相关的因素主要有以下两个方面：①所选的材料、规格、热处理状态等;②实际使用环境相关参数，如安装尺寸参数、环境温度等。针对所研究的减振器支架，综合对比公司现有同类产品及工程经验，最终选定了支架材料为Q355B(因减振器工作压力为4 320～6 240 N，以最大工作压力作为设计载荷条件，则对于常用工程材质Q235B，其屈服强度较低)。

试验设计参数如图2所示。支架安装尺寸受限于油缸两支架的位置，变动范围小，可作为固定尺寸；支架外翻用于安装减振器的翻边所处高度尺寸受限于油缸活塞杆中线尺寸，变动范围小，也作为固定尺寸；图中尺寸22.5 mm及38 mm为安装减振器所需空间尺寸，以确保减振器在工作过程中不会与支架发生碰撞。因此，最终选择支架板材厚度(mm)、减振器竖直安装尺寸(mm)以及水平安装尺寸(mm)为试验因素，以减振器支架工作应力Von Mises最大值(MPa)为响应对象进行试验分析。

图2 试验设计参数

2.2 试验因素水平选择及试验设计

2.2.1 因素水平选择

由上可知板材厚度、减振器竖直安装尺寸以及水平安装尺寸为因素进行响应曲面法规划设计，即三因素、两水平的模型。而本文选定了外切中心复合设计法(central composite circumscribed，CCC)，各因素水平分析如下：

(1)板厚。由于支架采用钣金结构，结合公司常备板材规格以及现有设备处理能力，确定板厚的取值范围为6～12 mm。

(2)竖直安装尺寸。考虑板厚内侧距离安装螺栓尺寸为15 mm(为保证充足扳手操作空间，最小尺寸为8 mm)，同时要控制车桥整体竖直方向的外廓尺寸，故选定竖直安装尺寸的取值范围为80～100 mm。

(3)水平安装尺寸。抱箍支架可调值为50 mm左右，主要考虑小轮距车桥应能满足50 mm的安装调整范围，转换为基准尺寸后，其取值范围为60～100 mm；而对于大轮距车桥，可通过增大支架尺寸来满足实际使用要求。

根据外切中心复合设计方法，得到20组试验数据。试验方案及仿真结果见表1。

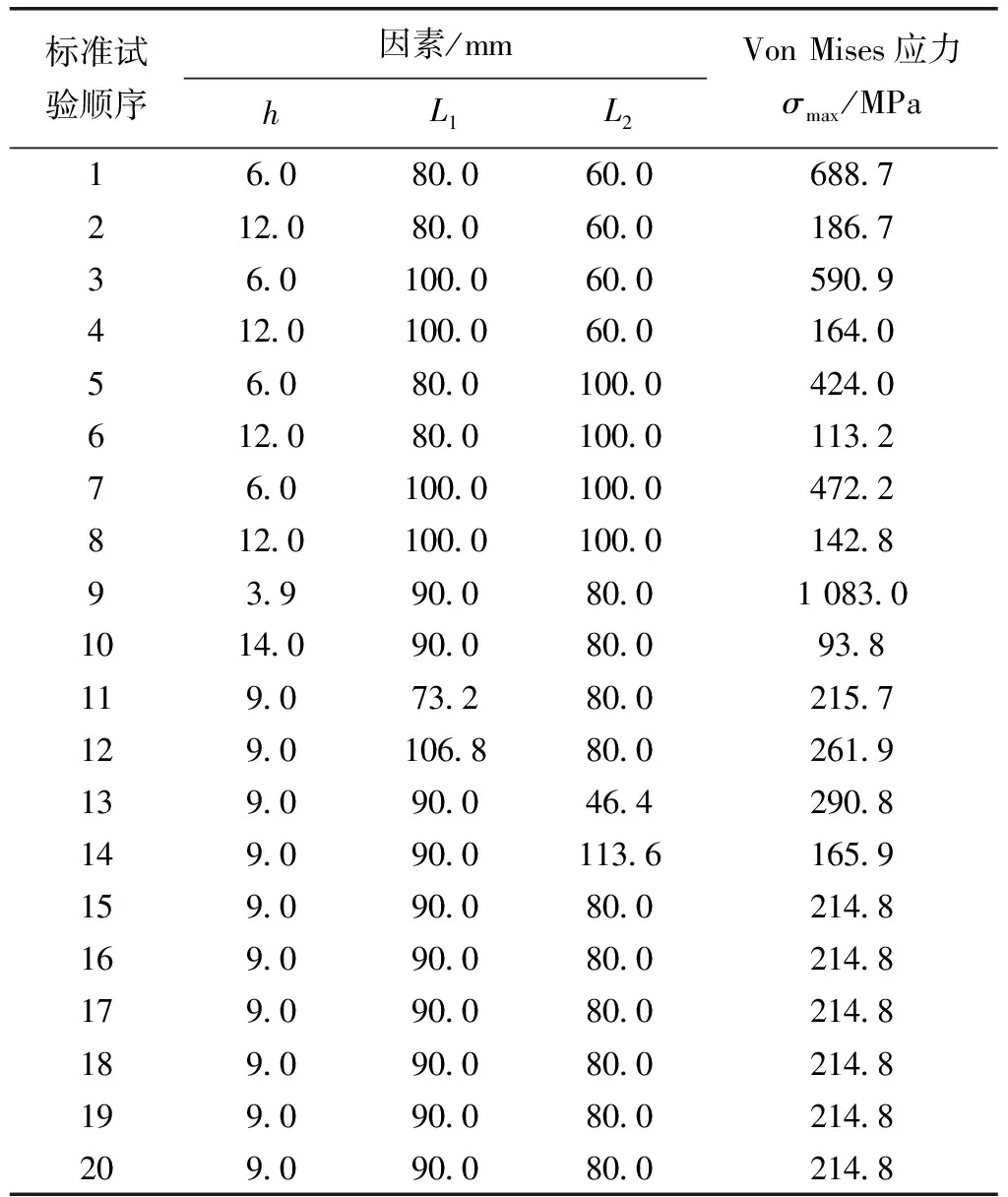
表1 试验方案及仿真结果

2.2.2 数据处理

响应分析模型如图3所示，利用SolidWorks软件按照表1参数建立响应分析模型，以支架侧面4个安装孔为固定约束面，以减振器安装孔为载荷作用面，载荷大小为6 240 N。依次仿真计算各组参数，并将结果汇集于表1。

图3 响应分析模型

2.3 公式拟合及评估

采用二阶模型进行响应曲面方程拟合，构建如下方程式：

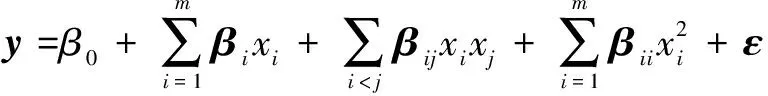
(1)

式中：=(，，…，)表示响应变量的试验数据向量即观测数值；=(，，…，，，…，，…，(-1)，…，，…，)表示模型的回归系数矩阵；=(，，…，)表示残差向量；和分别表示试验次数和影响因素数目。

利用Excel处理表1中数据，并将各因素转换代入，最终获得响应曲面方程为：

(,,)=4 296702 498-407149 603·-

22367 888·-19962 531·+0235 417··+

0601 458··+0123 938··+14386 035·+

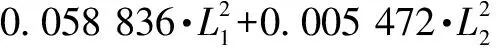
(2)

全二次响应方程方差分析结果见表2。

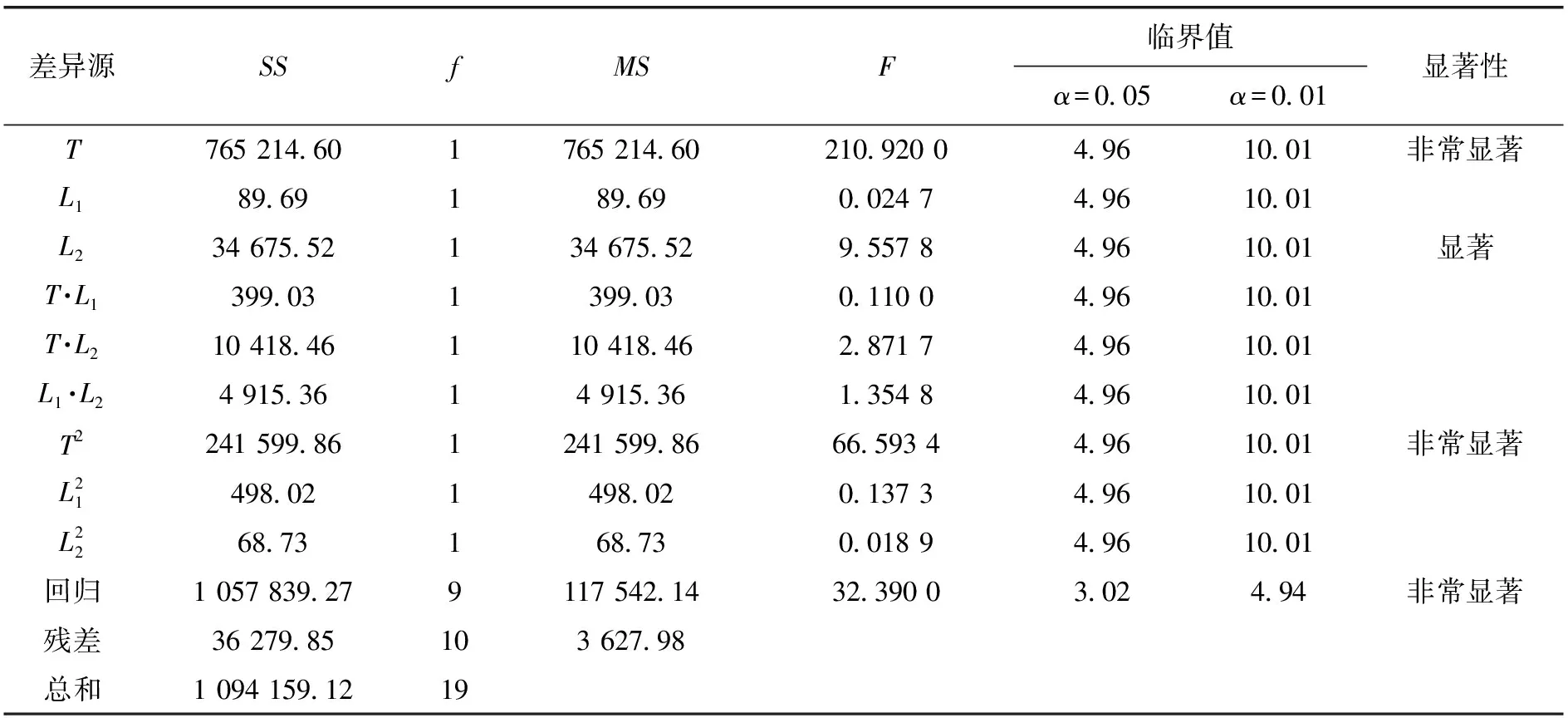
表2 全二次响应方程方差分析结果

由表2方差分析结果可知，该拟合方程具有很高的拟合度，可以作为预测支架工作应力的依据。同时，在各因素限定取值范围内，板厚与水平安装尺寸对支架最大工作应力影响较大，而竖直安装尺寸影响较小；交互项板厚与水平安装尺寸、竖直安装尺寸与水平安装尺寸对支架最大工作应力亦有影响；二次项中板厚起主要作用。因此在设计支架时，应优先选择合适的板材厚度，之后以水平安装尺寸为主并综合考量竖直安装尺寸来确定支架结构参数。

需要说明的是，为体现各因素在实际中的作用，本文未进一步将不显著因素剔除。

2.4 支架设计参数确定及仿真分析验证

2.4.1 支架设计参数确定

依照响应曲面分析流程，在得到拟合方程后，可进而分析获得优化解。而对于本文分析对象，支架板厚并非连续变量，需要根据国家标准规范以及公司库存等因素综合选定，而竖直及水平安装尺寸在实际中也都圆整取舍。因此在满足支架使用强度的前提下，结合拟合方程以工厂实际情况选定各因素取值更为实用。

查询公司近期原材料采购及库存情况得知，常用Q355B板材厚度规格为8 mm和10 mm，由表1所得仿真数据可知，选取8 mm板厚时支架工作应力较接近板材屈服强度355 MPa，故选定板厚为10 mm。同时，水平安装尺寸在取值范围内随着取值增大，同规格情况下所得支架应力值呈下降趋势，结合减振器抱箍支架的调整范围取其中值，即取25 mm，实现左右各25 mm调整范围，按实际基准位置尺寸圆整为90 mm。

考虑工程中常用安全裕度来衡量结构件的强度，其具体计算公式为：

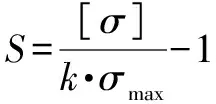
(3)

式中：表示安全裕度；[]表示许用应力(通常取材料的屈服强度),MPa；表示安全系数，可查阅相关资料选取，此处取1.35；表示材料所承受的最大应力值,MPa。

根据设计经验，暂取=1，代入式(3)可得=131.481 48 MPa。

对于竖直安装尺寸，可将上述已获得的参数代入拟合方程，即：

(10,,90)=4 296702 498-407149 603×10-

22367 888·-19962 531×90+0235 417×10·+

0601 458×10×90+0123 938·×90+14386 035×100+

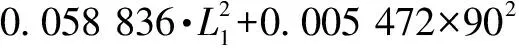
(4)

令(10,,90)==131.481 48 MPa，整理后得到关于的一元二次方程式为：

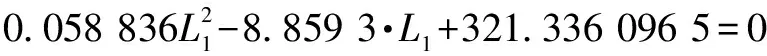
(5)

求解得到：=89666 6或=60909 61。

由计算结果可知，不满足要求(取此值时支架无法实际建模)，故舍去；因此取值,圆整后可得=90 mm。

将上述参数重新代入拟合方程，计算可得=132.048 5 MPa。该值与=1 时=131.481 48 MPa相比变化不大，而且此时安全裕度：

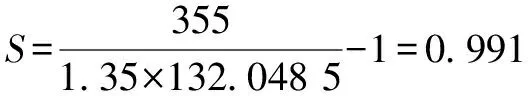
(6)

亦满足使用要求。故选取减振器支架设计参数(，，)=(10，90，90)。

2.4.2 仿真分析验证

以第2.4.1节所得参数建立支架实体模型，如图4所示。加载约束条件及工作载荷并进行仿真分析，得到支架Von Mises应力云图如图5所示。

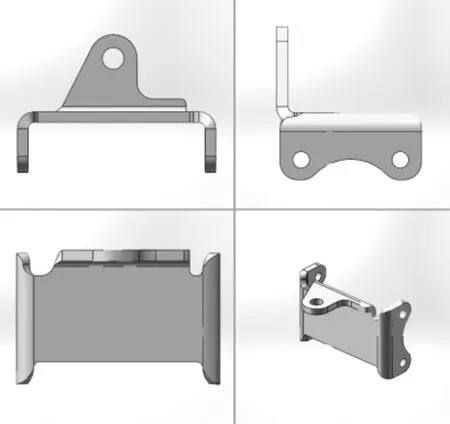
图4 支架实体模型

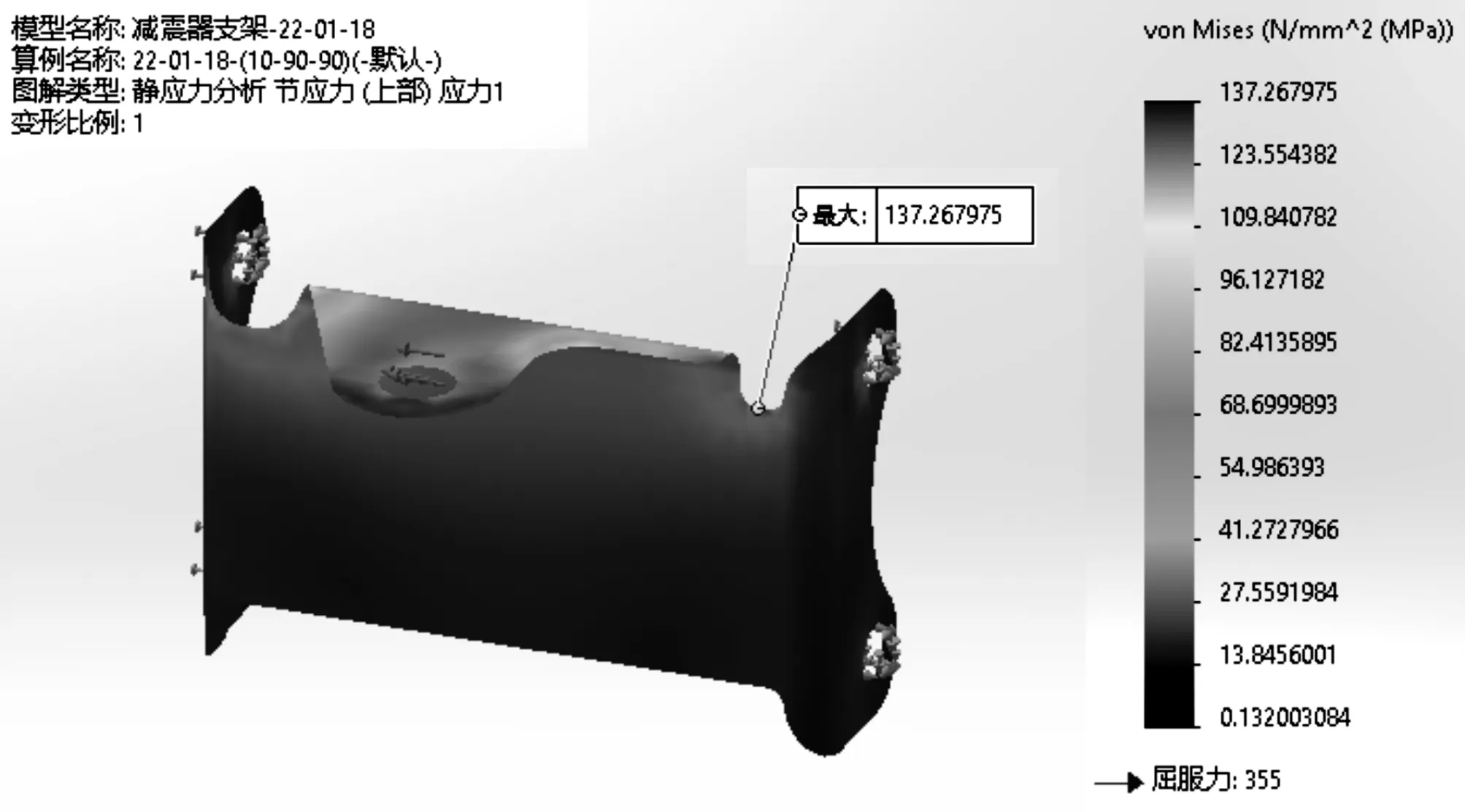
图5 支架Von Mises应力云图

由图5可以看出应力云图连续，最大应力值为137.267 975 MPa。此时，安全裕度：

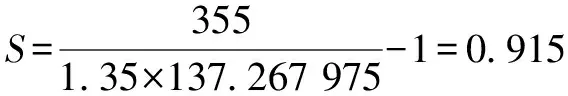
(7)

仍满足要求。而预测值偏差为:

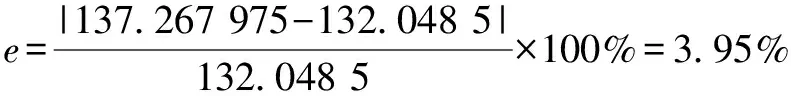
(8)

偏差较小，说明拟合公式有效可用。最终确定盘式车桥产品结构如图6所示。

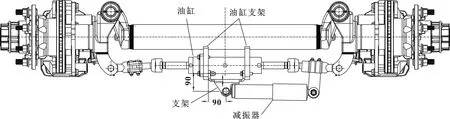
图6 盘式车桥产品结构

3 结论

利用响应曲面法对某盘式转向车桥的减振器支架进行了结构参数设计分析：

(1)得出了支架最大工作应力值与支架板材厚度、减振器竖直安装尺寸以及水平安装尺寸的拟合方程式；

(2)分析了3个因素在取值范围内对支架工作应力的影响程度，即板厚影响最大，水平安装尺寸影响次之，最后是竖直安装尺寸；

(3)依据上述拟合方程，并结合公司实际情况，确定了该款车桥的支架主要结构参数，并利用软件建模仿真与拟合方程预测结果进行了对比分析，显示拟合方程具有较高的预测精度，可以指导实际设计工作；

(4)利用拟合方程式，可以使后续同类配置但不同轮距车桥的减振器支架研发设计更为便捷，同时在具体装配过程中也可以利用该公式预测减振器调节安装位置后支架的工作应力状况。