非回转对称次波前退化下的干涉相干成像像差

吕思达，李明茁，胡海翔，薛栋林，张学军

（1. 中国科学院 长春光学精密机械与物理研究所中国科学院光学系统先进制造技术重点实验室，吉林 长春 130033；2. 中国科学院大学，北京 100049）

1 引 言

近年来，随着大口径光学元件需求的不断增大，大口径光学元件精度指标的要求越来越高，传统的加工与检测手段难以应对复杂的大口径自由曲面。干涉检测具有精度高、非接触测量等优点，广泛应用于大口径反射镜的检测，在实际的工程中具有重要的应用价值［1-2］。

按照补偿器的类型，干涉补偿检测可分为折射式、反射式和衍射式补偿法。其原理都是利用补偿元件对相位进行定量补偿，在提高检测精度［3-5］的同时，又可以对各种复杂面形进行高精度检测。例如，非回转对称表面进行干涉补偿检测时，需要设计出对应的计算机生成全息图（Computer Generated Hologram，CGH），入射波前经过CGH 补偿后，得到非回转对称波前，实现了对非回转对称表面的高精度零位补偿检测。然而，CGH 在补偿波前相位的同时，却引入了干涉相干成像像差，检测结果会受到影响，这种像差并不是由于制造精度产生的，而是因为补偿器存在衍射效应。尤其在大口径长焦距的光学元件检测中，成像像差与面形误差相互耦合，不能准确反馈原有的面形信息。而这种问题在小口径反射镜中影响较小，一般情况下其像差的影响域会通过焦深与景深来补偿。随着被检光学元件口径的增长，其检测光路越来越长。衍射效应带来的误差已经无法通过检测系统的景深与焦深来弥补，检测精度下降，严重影响整个检测系统中仪器的传递函数。传统干涉检验的误差分析仅考虑干涉和外界条件的情况［6-8］，往往忽略了衍射效应带来的成像像差，所以这种误差的影响还未有较为完善的理论分析。

研究发现［9-10］，干涉检测中衍射效应产生的误差主要表现为波前退化产生的像差，其主要表现为引入补偿器的同时，引入了成像像差，使得最终检测结果中所呈现的干涉条纹图案出现定位误差、相位模糊和振荡。Zhao 等利用Talbot 效应在一维情况下解释了成像像差产生振荡的原因，但这种方法只能进行定性分析，无法进行定量分析［9-11］。

本文从标量衍射理论出发，建立了非回转对称的次波前传播理论，并结合点源微扰的思想，基于微分几何原理建立了干涉相干成像像差模型［12］，定量分析干涉相干成像像差对于检测结果的影响，为提高检测精度提供了新的思路。

2 非回转对称的次波前传播理论

2.1 次波前退化的理论推导

次波前退化引起的干涉成像像差会使得检测结果出现偏差。图1所示为一个2 m 口径非球面的干涉补偿检测结果，其中像差具体表现为当对一个方向上对焦时，其他方向上呈现模糊的状态，即无法找到一个成像位置能获得全口径的理想成像。

图1 干涉相干成像像差对检测结果的影响Fig.1 Effect of interferometric coherence imaging aberration on detection results

由菲涅尔-惠更斯理论可知，波前传递可以理解为波前上的每一点都为一个小的点光源发散出球面波，此后的波前可以看作这些点光源发出球面波的“包络“形成的。因此，每个波前可以看作是次波前上每一点干涉叠加的结果。由标量衍射的角谱理论可知，在自由空间传播的传递函数如下：［13］

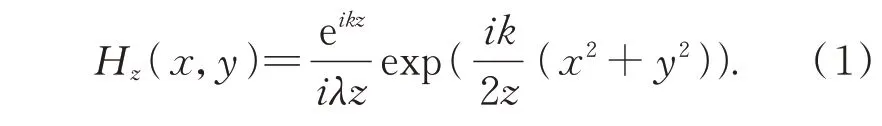
式（1）是标量衍射理论中描述球面波的波前传递情况。当引入CGH 补偿器之后，球面波虽然相位信息得到了补偿，但却引入了成像像差。这个像差主要表现为沿着CGH 表面的径向与轴向产生了场曲，使得通过CGH 的光束在成像空间上汇聚在了子午与弧矢两个焦点上。所以，针对非球面波传播上述的传递函数并不能描述其波前的传播情况，为了定量分析其波前传播情况，采用点源微扰的思想进行分析。由于常见的非球面分布都满足二阶连续可微的曲面，取其传播波前上的微元点进行分析，基于微分几何的原理，波前上任意一点的曲率可以看作两个正交曲率方向的矢量组合而成。而不同的曲率会导致其在光轴上的成像位置不同，这就不同于几何光学的假设前提，这里认为光线不仅仅只是一条理想的线，而是由一个点光源产生的一个很小角度锥体的光束。那么子午与弧矢两个方向的曲率在两方向上的光焦度不同，那么波前在成像面的光轴上出现两个焦点，即子午与弧矢方向的焦点，利用两焦点与像面位置之差（子午与弧矢方向上的离焦量）来构建其传递函数表达式，进而可以定量分析次波前的退化过程，如图2 所示。

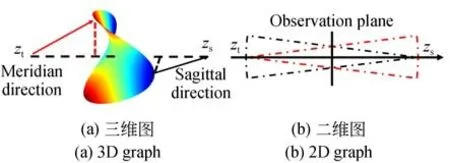
图2 非回转对称的离焦模型Fig.2 Out-of-focus model with non-rotation symmetry

基于标量衍射理论，对球面波传递函数的角谱表达式进行菲涅尔近似处理后，得到：

其中zt0，zs0为子午与弧矢焦点所在的位置。利用Mathematica 对式（3）进行傅里叶逆变换，得到传递函数的空域表达式：

将z-zt0，z-zs0设为子午与弧矢的离焦量zt，zs。引入子午与弧矢方向的离焦量后非回转对称的传递函数表达式如下：

其中：zs为弧矢方向的离焦量，zt为子午方向的离焦量。

2.2 仿 真

利用Matlab 对非回转对称的传递函数进行仿真分析，物平面尺寸设置为4 mm×4 mm，设置一个阶跃面作为参考。其中，发光平面尺寸为2 mm×2 mm，其余部分为暗面，从而获得一个理想阶跃的情况，其物平面模型如图3 所示。

图3 物平面仿真模型Fig.3 Object plane simulation model

为了方便观察其仿真现象，取子午与弧矢的离焦量为30 mm 时，观察分布在子午焦点、弧矢焦点和干涉仪焦点处其相位与振幅的变化情况。如图4 所示，通过对比发现，在对子午（弧矢）对焦的情况下，会出现一边锐利一边模糊的情况；而当介于两焦点之间时，会发现其子午和弧矢方向上都出现了振荡，其仿真结果与预期结果一致。这个理论模型为干涉检测成像像差模型的数值化以及定量分析提供了理论支持。

图4 次波前退化引起的成像像差对比Fig.4 Comparison of imaging aberrations caused by wavefront degradation

3 仿真模型建立

3.1 干涉相干成像像差模型的建立

基于非回转对称的次波前退化理论，得到了非球面波前的传递函数。整个波前退化的过程可以理解为携带真实面形信息的波前在经过传播过程中与干涉相干成像像差发生耦合，进而得到了退化后的波前，如图5 所示。类比点扩散函数（Point Spread Function，PSF）产生图像滤波效应的过程，将整个过程抽象为一个波前与调频函数的卷积过程，那么调频函数就是卷积核［14］。

图5 干涉相干成像像差模型Fig.5 Schematic diagram of interferometric coherent imaging aberration model

数学模型的建立从调频函数（卷积核）入手。首先，考虑到采样理想情况下的狄拉克采样形式，获得其调频函数的分布如图6 所示。观察其结果发现，仿真后所得到的调频函数的相位在边缘处的振荡十分剧烈，这就会导致最终像平面内存在过多的无效高频信息，而由于狄拉克采样，其振幅为常数，无法通过振幅的分布来截取其无效的高频部分，与实际情况不相符。

图6 狄拉克采样下卷积核相位与振幅的分布Fig.6 Distribution of phase and amplitude of convolution kernel for Dirac sampling

3.2 调频函数的数值化

为了抑制相位振荡的影响，采用改变卷积核的采样方式。由于高斯函数可以看作狄拉克函数的展宽，在保留其有效信息的同时，可以使其卷积核的振幅收敛，从而更好地解决其相位振荡的问题。所以，利用高斯采样的形式对卷积核进行数值化处理，如下：

为了提高计算的精确度，在考虑卷积核采样的同时，利用离散形式的高斯积分采样来代替原有的调频函数的表达式，即利用区域积分形式代替离散点采样形式，从而在保证计算精度的同时保证了计算速度。在新卷积核表达式的推导过程中，用误差函数代替积分取值的结果，进而在减小运算时间的同时保证计算精度。推导后得到其卷积核的最终表达式：

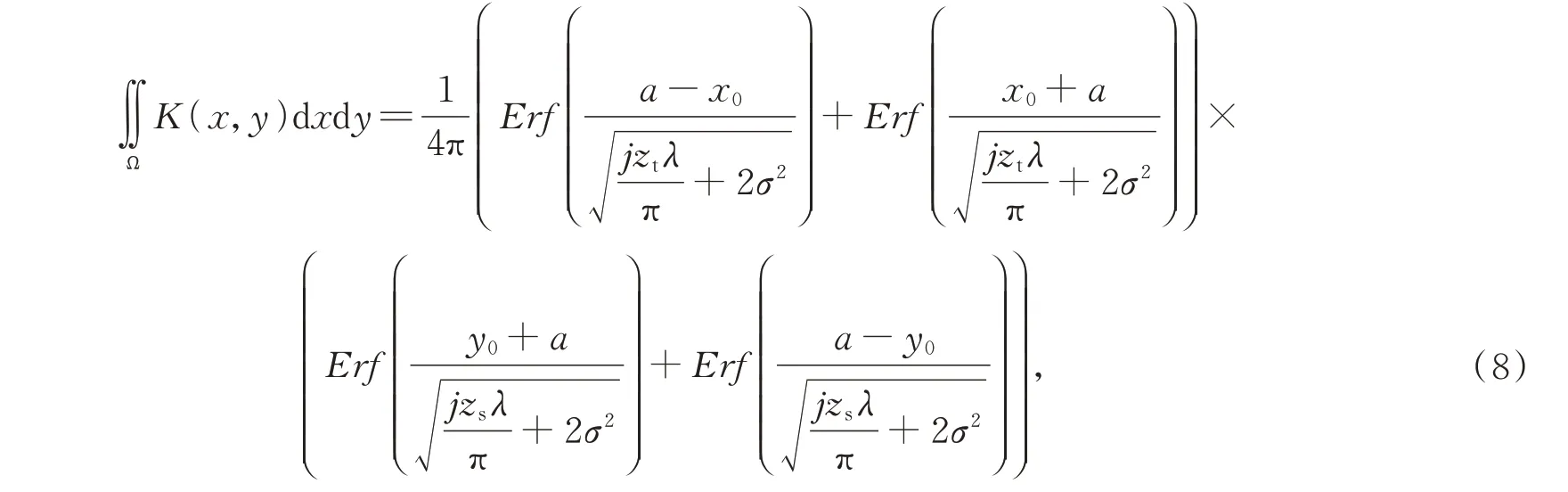
其中：zs为弧矢方向离焦量，zt为子午方向离焦量，a为采样尺寸的半宽度，σ为高斯采样的采样常数，（x0，y0）为卷积核采样点的坐标值。

3.3 仿真验证

在得到数值化的卷积核后，选取合适的数值进行仿真验证。取其离焦量为zs=-0.1 mm，zt=0.1 mm，σ=0.01，得到其卷积核的相位与振幅的分布如图7 所示。通过观察发现，虽然其相位的振荡很剧烈，但其振幅是收敛的，这也为卷积核尺寸的截取提供了依据。

图7 高斯采样的卷积核相位与振幅的分布Fig.7 Distribution of phase and amplitude of convolution kernel for Gaussian sampling

由于卷积核的振幅是收敛的，取一维下的卷积核振幅的分布，所以可以利用振幅来截取卷积核的尺寸。卷积核截取前后像平面的振幅与相位的分布如图8 所示（由于是两个方向正交，仅展示x方向上的相位与振幅的对比情况）。对比发现，改变采样方式，从而借助收敛的振幅所截取的卷积核所得到的像平面分布可以有效地抑制无效的高频信息，从而模拟出实际干涉成像中所呈现的真实情况。而离散形式的高斯积分采样结果的分布形式如图9 所示。与预期的结果一致，但运算速度提升了很多，为了保证算法的高效性，最终选用离散形式的高斯积分采样作为模型的调频函数的数值化方法。

图8 卷积核截取后的高斯采样的结果与卷积核未截取的对比结果Fig.8 Results of Gaussian sampling after convolutional kernel interception compared with convolutional kernel without interception

图9 积分高斯采样的相位分布与高斯卷积核结果的对比Fig.9 Phase distribution of integrated Gaussian sampling versus Gaussian convolution kernel results

3.4 干涉相干成像像差模型分析

首先对卷积核表达式进行分析，为了更好地分析卷积核的相位分布关系，对e 指数进行有理化，整理后观察其表达式分布，如下：

将式（9）中的前项分母设为-2p2后，将e 指数整理为：

其中：p为新的高斯函数的半宽，同时p也具有一定的物理意义。当z=0 时，p与σ相等。当离焦量增加时，p的宽度也随之展宽，也就说明影响的范围变大，即随着离焦量的增加，影响区域也越来越大。

在确定了卷积核矩阵的表达式与采样方式后，对结果进行进一步分析。由于子午与弧矢方向呈正交分布，彼此互不影响。取一维方向进行分析，利用小像差近似获得退化前的理想波前表达式如下：

传播后退化波前的分布表达式如下：

与理想情况下的对比发现，当σ=0 时，高斯采样转换为狄拉克采样形式，退化后的像面分布与理论推导的像面分布一致，故在原理上证明了高斯采样模型的正确性。

4 实 验

为了更好地验证干涉相干成像像差模型的正确性，设计一个柱面镜的检测实验光路，取一个柱面镜，并在其前方放置柱面镜对应的CGH 用于产生一个柱面波形，其中CGH 的直径为80 mm，主区域半径为70 mm，厚度为7 mm，其特征尺寸为15.2 μm，焦距为420 mm。在靠经柱面镜处放置一个十字光阑（用于观察其子午与弧矢方向的分布）。其工作原理与实际光路如图10 所示。

图10 实际光路与实验原理Fig.10 Actual optical path and experimental schematic

通过几何光学的光线追迹，算得子午与弧矢方向相对于干涉仪焦面的离焦量分别为zt=5 mm，zs=-1.4 mm，调节干涉仪的焦距，来模拟两个方向不同对焦的情况，基于干涉相干成像像差模型的仿真结果如图11所示。

图11 弧矢方向与子午方向的仿真结果Fig.11 Simulation results of sagittal and meridian directions

对不同位置进行检测，实验结果如图12 所示，并进一步分析得到它在子午与弧矢方向上的分布情况。

图12 子午与弧矢方向上的实验结果Fig.12 Experimental results in directions of meridian and sagittal

将实验结果与仿真结果进行对比，由于背景噪声等原因，获得的面形有一定的差异，选取实验结果的一部分作为验证结果。如图13 所示，实测结果与模型的残差分布，其残差结果均小于0.05waves。通过计算模型结果与实测结果的均方误差可得，其MSE 为0.001 1waves2，通过计算其对称平均绝对百分比误差（SMAPE）的值为8.26%，平均相对误差（MRE）为3.35%，由此说明该模型可以预测像差的影响情况。

图13 实测数据与模型对比及其残差分布Fig.13 Comparison of measured data with proposed model and its residual distribution

对比基于Talbot 效应与菲涅尔衍射积分分析方法得到的理论结果［7］（图14），通过计算求得理论值与实际检测值之间的对称平均绝对百分比误差（SMAPE）为10.23%，平均相对误差（MRE）为15.2%。显然，本文提出的模型的契合度更高，由此也验证了模型的正确性与准确性。模型的建立也从理论上分析出干涉相干成像像差的形成原因。那么对应干涉相干成像像差的解耦只需要对上述模型进行逆运算即可反解出真实的面形信息，也为干涉相干成像像差的解耦提供了新的思路。

图14 不同方法的结果对比Fig.14 Comparison of experimental results between different methods

5 结 论

本文对干涉补偿检测中干涉相干成像的像差进行了建模与仿真，提出了非回转对称波前传播理论，阐述了非回转对称波前的演化机理。结合细光束追迹与波前演化的混合分析方法，采用高斯积分采样的形式建立了干涉相干成像像差模型，从而获得子午与弧矢方向上离焦量与退化后波前分布的函数关系。实验结果表明，实测结果与模型的残差均小于0.05 waves，模型的均方误差（MSE）为0.001 1 waves2，对称平均绝对百分比误差（SMAPE）为8.26%，平均相对误差（MRE）为3.35%，模型的拟合结果明显优于亚利桑那大学提出的理论结果，由此验证了模型的准确性。本文提出的干涉相干成像像差模型不仅可以建立精确的干涉补偿检测结果的预测模型，也可以用于像差解耦，有助于提高高频处仪器的传递函数。