改进的动力学参数迭代辨识方法

朱成耀，张 波

(上海交通大学机械与动力工程学院，上海 200240)

0 引言

协作机器人具有拖动示教、碰撞检测、力/位混合控制等优势，这使得它在教育、加工、注塑和3C等领域中扮演着越来越重要的作用。协作机器人友好的动力学交互离不开精准的动力学模型，因此动力学参数的辨识工作十分重要。

摩擦力参数辨识是动力学参数辨识的重点和难点。目前,被广泛使用的摩擦力模型由库仑摩擦和粘性摩擦组成，但是无法描述摩擦的非线性特征。文献[1]中，使用和速度的指数成线性关系的粘性摩擦可以获得较好的实验效果。另外，机器人关节还存在正反向摩擦力不对称性，因此，建立更符合实际的摩擦模型可以提高动力学参数辨识的准确性。

动力学参数辨识的基本方法为最小二乘法[2]，最小二乘法保证了力矩误差的二范数达到最小。作为前者的改进，加权的最小二乘法则保证了动力学参数的方差达到最优[3]。然而上述方法均无法实现非线性摩擦模型的辨识。对此，Han等[4]提出了动力学参数的迭代辨识方法，该方法在提高动力学参数精度上表现了很大的优势，但是由于动力学参数众多，迭代的辨识方法需要消耗大量的时间。在动力学模型线性化后，基本惯性参数中部分参数对机器人关节力矩的贡献很小，剔除后并不影响动力学模型的精度，因此可以剔除。Janot等[5]在统计学意义上对基本动力学参数的作用进行了分析。

基于上述分析，为了获取更精准的动力学参数，本文引入了考虑速度指数和摩擦不对称常数的摩擦力模型，针对非线性模型采用一种迭代的方法进行参数辨识，引入F统计量剔除不影响关节力矩计算的基本动力学参数来提高迭代辨识的效率。通过实验验证了考虑复杂摩擦模型的迭代辨识的准确性，以及剔除影响小的参数后辨识的高效性。

1 动力学参数的迭代辨识

1.1 最小二乘法求解动力学参数

n自由度的串联机器人的动力学模型(考虑关节摩擦力)可以线性化为[6]

(1)

机器人的动力学方程可以简化为

(2)

假设有m个数据点，根据式(2)可以算出观测矩阵和观测响应为:

(3)

(4)

所以观测矩阵和观测响应的关系为

τ*=Y*p

(5)

因为mn>b，且Y*满秩，所以可以用最小二乘法求解惯性参数为

p=((Y*)TY*)-1(Y*)Tτ*

(6)

系统残差为

R*=τ*-Y*p

(7)

假设关节力矩的噪声是相互独立的,则力矩误差的协方差矩阵Λ是对角阵，且各关节力矩的噪声方差为

(8)

最小二乘法保证误差的二范数达到最小，加权最小二乘法可以使动力学参数的方差达到最小，即

p=((Y*)TDY*)-1(Y*)TD-1τ

(9)

D∈Rmn×mn为分块矩阵，其对角线由m个Λ组成。

(10)

因此，第i个动力学参数pi的相对标准差εpi为

(11)

辨识的动力学参数要满足物理可行性约束[7]，即辨识出的动力学参数应有实际的物理意义。对于关节j需要满足约束为

(12)

Ij为基于关节坐标系原点的惯性张量矩阵；mjrj为关节的一阶惯量;mj为关节质量;tr( )为迹函数；E3为三阶单位矩阵;>0表示矩阵是正定矩阵。

1.2 基于迭代的辨识

最小二乘法虽然简单，但是在辨识过程中无法考虑物理可行性约束，没有将采样数据的异常点剔除，也无法对复杂的摩擦力进行辨识，这都会影响动力学参数辨识的精度。因此，本文将最小二乘法改为有约束的优化问题，对辨识问题转化成三环迭代优化问题，以此提高动力学参数的辨识精度。

a.关节通道误差归一化迭代的内环。

如果去掉机器人关节噪声独立的假设，那么力矩误差的协方差矩阵便不再是对角阵，新的协方差矩阵为

(13)

由于协作机器人的1～3关节力矩要比4～6关节的力矩要大很多，因此误差的量级也不相同，因为要对式(7)中各关节通道的误差进行归一化处理，即

(14)

b.异常采样数据剔除的中环。

实验中采集的数据异常点会对最小二乘法的辨识结果产生很大影响，因此需要在辨识的过程中去除。定义迭代的权重变量W：

(15)

(16)

W∈Rmn为权重变量，We∈Rmn×b为扩展权重变量，其由b个W扩展组成；.*为按元素乘符号。

本实验采用最简单的T类硬权函数[8]，当归一化残差绝对值小于阈值φ时，该数据权重为1，否则为0。在既保证异常数据被清除，又保证剩余数据是正态分布的情况下，阈值φ=2.795。

去除异常数据后，则对动力学参数进行求解。由于需要考虑物理可行性约束，将最小二乘法转化为带约束的优化问题[9]，即

(17)

pb为与摩擦参数无关的基本惯性参数；pd为原始参数向基本惯性参数转换时被简化的参数，这部分参数是不确定、无法辨识的；pf为与摩擦相关的基本惯性参数；pt为变换后的基本惯性参数和不确定参数；G为原始惯性参数向基本惯性参数转换的映射矩阵；pt( )取pt参数集中对应的参数。该优化问题可以用MATLAB工具箱CVX的SDP模式获得最优解。

获取动力学参数后，计算出归一化的残差为

R#=τ#-Y#p

(18)

噪声的协方差更新为

(19)

E#为归一化残差R#的变形。这一过程即内环的关节通道误差归一化迭代。

内环稳定后，对计算出的归一化误差数据进行加权，更新权重变量，即

Wcur=min(Wpre,T(R#))

(20)

min( )为取较小值函数；T( )为T硬权函数。该迭代公式表明之前迭代异常的数据将不再参与计算，每次迭代去除新的异常数据。这一过程即中环的异常采样数据去除迭代。

c.指数粘性摩擦模型辨识的外环。

一般情况下，摩擦力模型被简化为库仑摩擦和与速度成线性关系的粘性摩擦,即

(21)

实际机器人关节摩擦力模型可表示为

(22)

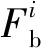
(23)

首先获取关节力矩中摩擦力的部分，即

(24)

对这部分摩擦力用式(22)进行拟合，即

(25)

这就是外环的指数粘性摩擦模型辨识迭代。该优化问题可以用MATLAB函数fmincon求解。

2 降维的迭代辨识

在动力学参数辨识的结果中，有些参数非常小，与此伴随的现象是相对标准差较大，这些参数几乎不贡献关节力矩，因此剔除这些参数不会影响力矩精度。在辨识之前找到这些参数可以降低内环优化问题的维度，提高辨识效率。

2.1 F检验

F检验是一种统计检验方法，主要用于方差齐性检验和方差比率检验等。它是在零假设之下，统计值服从F分布的检验。F检验可以进行线性回归方程整体的显著性检验，即线性方程回归系数中的1个或多个是否适用于估计母体。

使用F检验之前需要进行KS检验保证分析的数据符合正态分布。

2.2 动力学参数剔除

迭代的参数辨识的归一化残差通过KS检验(MATLAB中的kstest函数)满足正态分布：R#～N(0,1)。因此，可以使用F检验剔除对力矩没有显著影响的动力学参数[10]。

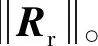
c.计算统计量F。

(26)

显著性水平α=0.05，自由度n1=b-br、自由度n2=mn-b≈∞，查阅F分布表获得边界值Fth。若F≤Fth，则说明剔除的参数对力矩就算精度没有影响，继续降低相对标准差阈值ε0，ε0根据经验可以从60向20递减直到F检验失效。

2.3 降维的迭代辨识

通过F检验后，对关节力矩计算精度有显著影响的参数变为br。式(17)的优化问题变为

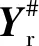
由于该优化问题处于三环迭代的最内层，是计算最频繁的优化环节，将动力学参数降维后将会提高辨识的效率。

3 动力学参数辨识实验

动力学参数辨识的实验在溱者协作机器人Chin7上进行，表1为Chin7的MDH参数。

表1 Chin7机器人MDH参数

3.1 激励轨迹的设计

为了保证机器人的动力学特性被充分激发，需要设计轨迹保证式(5)中的观测矩阵满足持续激励条件。根据文献[11]，机器人动力学参数辨识轨迹通常采用五阶傅里叶级数。

(28)

wf=0.2π为基频，轨迹周期T=10 s。每个关节轨迹有10个待定参数。

根据文献[12]，以式(5)的观测矩阵的条件数为优化目标，满足机器人的速度、加速度约束，求解

(29)

为了简化约束提高辨识效率，该优化问题没有将位置和速度起始点和结束点约束为关节原点。在运行激励轨迹之前可以各设计1段五阶多项式轨迹作为启动轨迹和收尾轨迹。本次实验采用的激励轨迹如图1所示。

图1 动力学参数辨识的关节激励轨迹

在获得降维的参数以后，可以用降维的观测矩阵作为优化的目标，观测矩阵的列数减少，同样可以提高激励轨迹优化问题的求解速度。

3.2 数据处理

将图1的激励轨迹输入到机器人控制器中运行，重复运行5次以便对数据集取平均降低误差。机器人以1 kHz的采样频率获得关节电流和关节角度。计算观测矩阵时需要关节的速度和加速度，因此先对位置进行滤波再一次差分和二次差分获得速度和加速度[13]。采用截止频率为7.5 Hz(轨迹最高频率的15倍)的四阶巴特沃斯滤波器(MATLAB中的butter函数),进行零相位滤波(MATLAB中的filtfilt函数)。关节电流和关节力矩成正比，在使用式(9)辨识时，采用和处理位置信号相同的滤波器。使用式(17)辨识时，由于迭代辨识中环的存在，电流不需要进行滤波即可参与计算[4]。

3.3 验证辨识效果

a.最小二乘法和迭代辨识法。

利用处理好的数据，分别使用最小二乘法直接计算机器人的动力学参数(方法A)，再用迭代辨识的方法计算机器人的动力学参数(方法B)。

求解出动力学参数后，再设计1条验证轨迹，观察验证轨迹的实际力矩和使用动力学参数计算出的预测力矩是否吻合，评价标准相对RMS为εRMS，即

(30)

2种方法的εRMS如表2所示。由表2可知，迭代的辨识方法考虑了物理可行性约束、对异常采样数据进行了剔除以及建立更符合实际的摩擦模型，其辨识出的动力学参数计算出的关节力矩都更接近实际力矩。证明迭代的辨识方法获得的动力学参数更加准确。

表2 3种辨识方法的验证轨迹各关节εRMS

b.降维前后的迭代辨识方法。

使用式(9)和式(11)求解动力学参数和相对标准差。然后使用F检验去除无影响的动力学参数，相对标准差阈值ε0从60开始以5的梯度递减直到F检验失效。在Chin7上，在ε0=35时，失效的参数为15个，在显著性水平α=0.05时，自由度n1=b-br=15、自由度n2=mn-b≈∞，查阅F分布表获得边界值Fth=1.68，求解F=1.604 2，满足F检验。此时，机器人的动力学参数由58个降为43个。

原始基本动力学参数的迭代方法(方法B)和使用F检验降维后的动力学参数的迭代方法(方法C)辨识的εRMS结果和验证轨迹力矩图如表2和图2所示。

图2 降维前后的验证轨迹各关节力矩

4 结束语

针对机器人动力学参数辨识需要考虑物理可行性约束、去除异常采样数据、建立更符合实际的摩擦力模型问题，本文使用了迭代的辨识方法。并针对迭代方法时间成本高的问题提出了一种改进的迭代方法，引入F检验的统计学方法，以相对标准差εpi作为基准递减至F检验失效，获得对关节力矩贡献很小的基本动力学参数并进行剔除，参数经过剔除后再参与迭代辨识。通过实验发现：

a.用三环迭代的动力学参数辨识方法比直接用最小二乘法获得的动力学参数精度高。

b.使用F检验降维后的参数参与的迭代辨识在没有损失各关节力矩精度的情况下，大大提高了三环辨识的效率。

c.未来将在降维的动力学模型框架下，考虑关节在低速下的Stribeck摩擦模型，从而进一步提高动力学参数辨识精度。