基于改进A*算法的四向穿梭车路径规划

余嘉雄，白红星

(1.浙江凯乐士科技有限公司，浙江 嘉兴 314000；2.武汉大学，湖北 武汉 430072)

0 引言

跨巷道多层四向穿梭车仓储系统(以下简称多穿库)是一种密集存储系统，与普通立体仓库相比，可以多层多区域并行作业，通过提升机连接各层，提高单位时间出库总量，缩短分拣时间，被广泛应用于“货到人”订单拣选模式。

在密集仓储系统中，常用的搬运设备为智能件箱式四向穿梭车(以下简称穿梭车)，它是一种智能的搬运设备，结合编码器、光电传感器和摄像头等技术实现实时位置的精确定位及货物与车体姿态检测；而仓储系统中的智能化穿梭库调度系统，则负责根据任务类型进行组合，调度穿梭车进行循环式作业，确保整体作业效率。由于穿梭车无需人员操作，运行速度快且智能化程度高，适用于各种物流存储系统，能够促进单元物料快速实现自动输送，但这在很大程度上取决于系统执行复合作业的路径是否合理。

对于穿梭车路径规划问题，当前应用较为广泛的方法为改进自动导引运输车AGV路径规划方法。然而，穿梭车是基于轨道行进的高速运行物流搬运设备，其轨道与AGV路网布局差异大，穿梭车无法具备AGV近距离跟随、短距离刹车和就近可变换通道的能力，因而其路径规划与AGV有类似的地方，同时也存在较大的差异。

刘国栋[1]提出了多 AGV 调度系统中的两阶段动态路径规划方法，被国内AGV厂商在实际应用中广泛采用，但是这种方法在路径规划时没有考虑正在执行任务车辆路径之间的相互影响，使得对地图以单向路径为主，降低了系统灵活性，而且也增加了系统实时路径冲突处理的难度与复杂程度。张喜妹[2]对多台类Kiva机器人的碰撞问题给出了处理机制。Sharon等[3]使用CBS方法(conflict-based search)对多车路径进行规划，适用于小规模的路径冲突情形，时间粒度小对软硬件要求高，实际应用中困难较大。李伟光等[4]提出基于改进A*算法的AGV路径规划，通过增加转弯因子，降低AGV的转弯次数，提升路径优化效果。万千[5]在基于CBS算法的物流分拣多AGV路劲规划的研究中，对基于冲突的多车路径规划的方法进行了优化。杨玮[6]、周奇才[7]、聂峰[8]等提出了对双载式多层穿梭车仓储系统复合作业路径优化研究，实现了多路径的优化方法，分别从多种应用场景角度设计优化算法。冉文学等[9]实现了动态立体仓库中穿梭车货到人多目标拣选路径的优化，将禁忌搜索算法应用到穿梭车拣选路径优化中。

本文从穿梭车库控制软件系统中路径搜索实际应用出发，提出了一种改进A*算法的路径规划算法，在搜索过程尽量减少各车在各路径节点行驶范围内与其他车辆的路径的点交叉与边冲突，既保证系统路径搜索时效要求，同时降低实时路径冲突处理规则的复杂程度，在穿梭车不同时间搜索路径时，动态考虑路径占用情况，从而保证整个系统的稳定高效运行。

1 问题描述

跨巷道多层穿梭车库，分别由穿梭车、入库提升机、出库提升机、层入库暂存位、层出库暂存位、纵向/横向移动通道、出/入库提升机、换层提升机及存储货位构成,具体如图1所示。

图1 多穿库平面布局

穿梭车行驶最大速度为4 m/s，加速度为2 m/s2。由于其速度快，减速停止距离大，因此，采用分段定位的方式进行定位，将路径分段执行并进行路径资源的占用与释放，而在停止位进行路径状态更新与位置校对。

多穿库路径规划需要解决的难题之一，是在任务聚集时，多辆穿梭车路径干涉问题。因此，期望能考虑正在执行任务的车的路径基础上，找出其干涉少、转弯少的路径，而不是单纯的最短路径(路径干涉会有等待)。

而在路径干涉检测中，如果只考虑2点之间最短路径，不考虑各穿梭车当前位置，则路径干涉过多，使得结果不理想。因此，需要对各车位置进行区分以及其占用路径情况，进行动态路径规划，所得结果更加合理。

对于穿梭车之间的路径干涉，分为如下3种情况：

a.路径成环，多个车辆运行形成多条路径，从而得到有向环，路径成环后造成路径封闭，从而不能进行后续工作。

b.点冲突，从不同方向在相同点发生碰撞。

c.边冲突，在相反位置路过2个点连边。

2 最大可靠路

在有向图网络中，往往需要利用已知的各边的可靠性概率，求出指定起始点S到目标点T的1条可靠性概率达到最大的路，此路称为由S到T的最大可靠路[10]。

在网络G中，各顶点间有向路完好概率为0≤pi,j≤1，定义为

(1)

为了利用最短路求解方法，2点之间距离矩阵为A=(ai,j)n×n，将pi,j做如下变换，即

(2)

ai,j中初始值为a0(除为0的值与∞外)，并根据点边占用情况进行处理。

多辆穿梭车路径干涉时，需对有向路的完好概率进行调整，实际应用时，保证车辆数增加初始阶段权值变化大，后续逐渐平缓，避免后续任务找不到路。

在最大可靠路基础上，做了一些调整，即将点所经过的边数进行汇总。

将对各路径中所有经过的边i→j即从i点出发到j点的边，进行总数量统计，对每条路径分别计算组成的边并进行汇总：Bi,j=Bi,j+1，而反向边为Bj,i=Bj,i+tmpR。

将冲突次数进行如下变换，即

(3)

对于距离矩阵A=(ai,j)n×n，ai,i=0。根据地图规模，设定N值，满足路径点对于多辆穿梭车占用敏感程度的要求。

3 改进A*算法

A*算法是目前应用最多的一种路径查找和图形遍历算法。可准确进行查找和筛选，算法性能优越。各节点级别由A*算法表示为

f(n)=g(n)+h(n)

(4)

f(n)为节点Vn的综合优先级；g(n)为节点Vn距离起点的代价；h(n)为节点Vn距离终点的预计代价。

穿梭车主要向4个方位运行，通过曼哈顿距离表示为

(5)

在栅格地图中，使用RCA(对于当前点的状态描述，R为地图行标，C为地图列标，A为方向)方式记录位置与状态，点的状态增加了方向A维度。方向记录方式如图2所示，如S(3,2,2)→T(2,2,2)为由S点(第3行第2列，方向向上)出发移动到T点(第2行第2列，方向向上)。

图2 穿梭车行驶方向示例

3.1 路径搜索基本思路

a.使用RCA方式进行记录位置与状态，点的状态增加了方向维度，使用A*的迭代结构进行计算。

b.在增加新点时，只考虑2点之间的邻接属性，不考虑方向，方向由起点到终点来确定，2点之间距离通过距离矩阵计算，转弯通过起点与目标点方向差异进行计算得出，避免了考虑方向维度产生的大量解的情况，减少转弯数量以及由于转弯计算产生的额外的距离值。

c.在新添加点时，添加其他车辆路径点约束冲突检测(边重合与边冲突数量)，计算重合边数及冲突边数，并根据函数计算添加的额外距离值。

d.终点方向通过最终方向与终点需要方向进行1次调整，使得最终方向与终点方向一致。

3.2 两点间距离以及冲突、转弯的额外增加距离值计算

数据说明，fromNode为每次迭代搜索时的一小段路径的出发点，toNode为每次迭代搜索时的一小段路径的目标点，startNode为整个任务的起点，goalNode为任务的终点。

a.距离值计算。

根据距离矩阵计算fromNode到toNode点的距离，即

D=A(fromNode,toNode)

(6)

b.边值计算与距离矩阵更新。

对路径边fromNode→toNode进行数量统计：

M(fromNode,toNode)=M(fromNode,toNode)+1

(7)

A(fromNode,toNode)=

(8)

计算有向边toNode→fromNode的总数量，InverseEdgeWeight为反向边变数放大权值，为常数，具体计算式为

M(toNode,fromNode)=M(toNode,fromNode)+

InverseEdgeWeight

(9)

通过将反向边的数量放大，从而将其在距离矩阵计算中统一处理，使得在搜索过程中，自动避开反向的边。但是在一定有反向边情形下，会选择反向边较少的路径。距离矩阵计算式为

A(toNode,fromNode)=

(10)

c.转弯距离值计算如式(12)所示：

(11)

transCost=a0×(1+transFlag)

(12)

d.f、g、h值的计算。

首先，根据距离矩阵计算fromNode到toNode点的距离，即：

D=A(fromNode,toNode)

(13)

g(toNode)=D+transCost+g(fromNode)

(14)

其次，计算启发函数值，由于采用曼哈顿距离，需要对其进行外加权值，才能与当前距离在同一量级进行比较，因此，其值取曼哈顿距离与距离D的乘积，即

(15)

toNodex、goalNodex为toNode、goalNode点x方向坐标；toNodey、goalNodey为toNode、goalNode点y方向坐标；g(toNode)为toNode距离起点的已寻路径的距离值；h(toNode)为toNode距离终点的预估的距离值，即

f(toNode)=g(toNode)+h(toNode)

(16)

3.3 任务路径搜索算法流程

在系统实际执行中，任务是不间断进入的，分别在不同时间进行搜索任务路径，而不是同时进行各任务路径的搜索。因此，多个任务分别进行搜索时，其任务搜索流程如图3所示。

图3 多车任务搜索流程

在每次任务搜索中，单任务搜索算法流程如图4所示。

图4 单车任务搜索算法流程

4 实验仿真与分析

为了验证本文方法的有效性，在MATLAB中进行了仿真。以图5所示穿梭车地图为例，分别通过改进A*算法生成每个机器人的路径，黑色正方形表示穿梭车库的货架货位(车不能进入)。穿梭车根据任务下发先后时间确定其路径搜索顺序，主要考虑的元素为：

a.路径中边冲突数量，即车辆路径行驶的反向边数量。

b.转弯次数。

c.路径点冲突数量，即重复经过的点数量。

在穿梭车执行任务中，边冲突需要更换路径才能继续执行任务，花费时间较长，转弯也需花费较长时间，点冲突则需进行等待，因此，结果比对中，主要参考这3个元素。对于穿梭车运行过程，有如下简单规则：

a.1段路径只能直行(横向或纵向)。

b.行驶路径段资源独占。运行1段路径，不能有其他车辆在此路段有相同的路径节点，即独占路径段上的所有节点资源。

c.路径段上节点资源释放为行驶的当前段路径，穿梭车停在终点时，释放其他点资源。

选取2个任务情形进行比较，分别为：[13,26]→[3,14]，[8,5]→[18,26](点分别由行数与列数进行组合表示)，其结果如图5所示。

图5 算法双车路径示例

根据穿梭车行驶规则，对上述路径进行行驶过程分解。由于A*与Dijkstra路径相同，所以只对A*与改进A*算法进行分析比较(后续距离单位为网格地图中方格之间的总长度，方格边长均为1)，具体结果如表1所示。

表1 2车路径运行解析

在A*搜索路径情形下， 2号穿梭车需等待1号穿梭车在N2点释放路径点资源时，才能开始执行任务，因此，整体完成距离变长，计算并运行距离数为25；在改进A*算法搜索路径情形下，2辆车路径没有干涉点，因此，可以同时并行运行，并运行距离数为19。比较分析结果如表2所示。

表2 2车路径数据比较

在多穿库系统实际执行过程中，根据穿梭车运行规则，车辆路径之间的距离最少，参考意义不是最优先的，因为路径之间存在交叉的或者某段路径边冲突，则使得实际执行中等待加长，且多辆车路径交叉严重时，还会造成路径之间死锁。因此，实际执行中需要参考穿梭车之间路径边冲突数量、转弯数量以及路径点重复程度，使得等待时间变少，整体执行效率提高。

由表2可知，采用改进A*算法后，穿梭车的路径在边冲突数量、转弯数以及并行行驶时间上明显优于其他方法搜索的路径，可显著提高整体运行效率。

由于边冲突可能会产生重新搜索路径(换路策略，不在本文讨论范围内)，因此在实验中，未统计时间并行运行中的时间长度。随机产生任务(每种情况随机100次任务)，根据车数与产生任务数量进行结果比较(取均值)。进行数据模拟，参数设置为a0=0.9，InverseEdgeWeight=100，N=30。模拟结果统计如表3所示。

从表3可知，改进A*算法可有效减少边冲突数量。随着车辆数量增加情形下，各算法对于边冲突数量均有增加，但是改进A*算法的增加数量显著少于其他算法，而对于计算时间的增加相对于A*算法来说增加很少，差别在毫秒级，因此在实际应用中有较好的适应性。

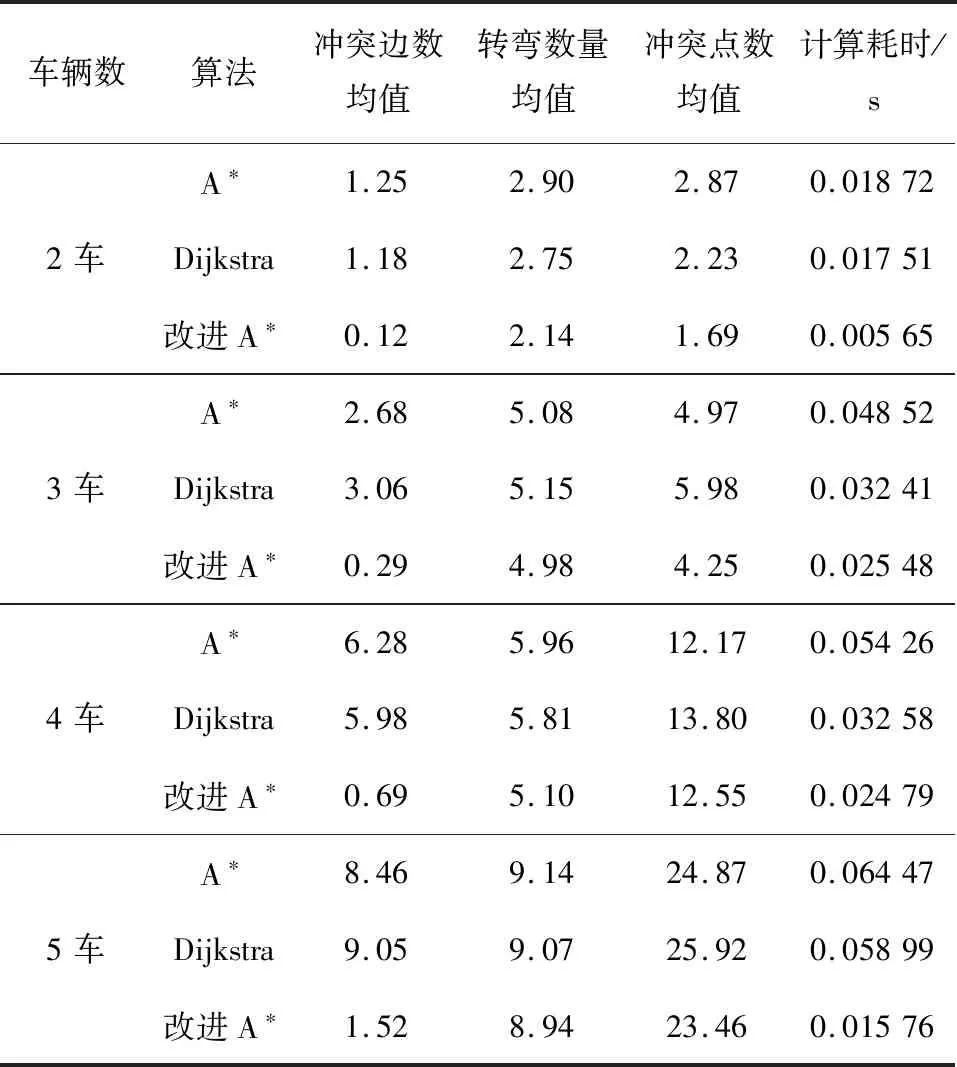
表3 模拟实验各算法数据结果比较

5 结束语

通过产生大量随机任务，使用改进A*改进算法进行穿梭车库多车路径规划，较好地解决了当前单独使用A*方法存在的路径方向冲突、路径转弯数量不可控的问题，验证了改进算法快速、有效性。通过调整配置权重参数方法，可以很好地应用于实际的穿梭车调度系统中。而在算法中，可以通过改变冲突变数与转弯数权值方式，重新计算距离矩阵，达到改变其优先顺序的目的，因此，在实现过程中可通过参数调整，较好地适应不同实际布局情形下对结果的要求。算法中存在一些可优化的地方，加入时间窗后，可以更精确地对路径交叉的部分进行控制，从而使等待时间降低到最少，提高多穿库整体运行效率。对于穿梭车库路径规划问题的研究，能够为箱式立体库提供一定的理论基础与思路，提高穿梭车的效率，并为大规模穿梭车库调度系统研发与应用提供借鉴，具有较强的应用价值和现实意义。