基于VMD联合RCMDE的特定辐射源识别方法
宋子豪,程 伟,李敬文,李晓柏
(1.空军预警学院 预警情报系,湖北 武汉 430019;2.空军预警学院雷达士官学校 教研保障中心,湖北 武汉 430019)
0 引言
特定辐射源识别(Specific Emitter Identification,SEI)技术是非合作通信领域的关键技术,特征提取作为SEI技术的关键步骤,对识别性能有着极为重要的影响。在日趋复杂的电磁环境中,用于SEI的典型一维特征,如瞬时频率[1]、脉冲幅度[2]、脉冲宽度[3]和功率谱密度[4]等,因表达信息能力受限等常常引发识别性能下滑等问题。因此,一些包含更多指纹信息的高维度特征被应用于SEI领域,如短时傅里叶变换[5]、双线性时频变换[6]、小波变换[7]、同步挤压小波变换[8]和希尔伯特谱[9]等。但是,将上述高维度特征数据输入至传统分类器中训练模型时,计算负担较重、耗时较长。
针对上述问题和通信辐射源信号存在的非线性非平稳特点,部分学者提出可以提取辐射源信号时域序列或频域序列的熵复杂度特征作为特征向量,完成SEI工作[10-12]。上述方法存在的问题有:部分变换方法在处理非线性非平稳信号时存在局限性;直接从原始信号或变换后序列的结果中提取特征区分能力有限。
基于上述考虑,一些学者开始尝试先利用经验模态分解(Empirical Mode Decomposition,EMD)[13]、经验小波变换(Empirical Wavelet Transform,EWT)、变分模态分解(Variational Mode Decomposition,VMD)等算法将原始信号分解成多个本征模态函数(Intrinsic Mode Functions,IMF)后进行熵复杂度特征提取的SEI方法。由于EMD算法存在模态混叠和端点效应问题,EWT不适用于非线性时间序列的分析,VMD算法在SEI领域得到了更为广泛的应用。国内外学者提出了诸多VMD联合熵复杂度特征的SEI方法[14-15]。但是,多数方法仍然将单一尺度熵作为识别特征,使得识别性能的上限不高。基于多尺度熵的方法选取的特征仍然以多尺度排列熵(Multi-scale Permutation Entropy,MPE)和多尺度样本熵(Multi-scale Sample Entropy,MSE)为主,前者未能考虑幅值之间的大小关系,后者的计算速度慢、受突变信息影响较大。
本文提出了一种基于VMD与精细复合多尺度散布熵(Refined Composite Multi-scale Dispersion Entropy,RCMDE)的SEI方法[16]。由于RCMDE拥有更高的计算精度和更强的细微特征提取能力,使得该方法克服了过往基于VMD和多尺度分析方法的弊端和应用上的不足,以更小的耗时获得了更高的识别准确率。
1 辐射源指纹特征
辐射源个体的细微差异主要来源于辐射源系统中元器件的物理层面。一个典型的辐射源发射机系统如图1所示。

图1 典型辐射源发射机系统Fig.1 Typical emitter system of radiation source
在图1中,经数字信号处理的基带信号被数模转换器转换为模拟信号,模拟信号被滤波后经过正交的上变频器,最后被送入功率放大器。功率放大器的作用是增大信号的强度和传播距离。辐射源的个体特征主要来源于系统内各元器件的容差,容差效应使得电子元器件的实际参数值与标称参数值发生了偏差[17]。容差效应在各电子元器件中普遍存在,其中,频率源和功放的容差效应对辐射源个体特征的形成影响较大。在辐射源发射机系统中,频率源的稳定度受振荡电路工艺、电源电压变化、机械振动等因素影响,难以人为控制,常常引发不可避免的载频偏移及相位噪声。此外,实际应用情形下的功率放大器的输入输出曲线不可能严格线性。随着功放输入信号功率或幅度的持续增大,输出信号将不可避免地产生非线性失真,而不同辐射源个体的非线性曲线则存在较为明显的差异,上述因素的存在为辐射源个体发出的信号添加了“指纹”[18]。然而,伴随着频率源的晶体品质以及制作工艺的不断提升,不同辐射源发射机载波频偏越来越接近,使得载波频偏已难以体现辐射源的个体差异[18]。因此,本文主要围绕影响辐射源个体特征的相位噪声以及功放非线性特性进行建模分析。
1.1 相位噪声
相位噪声是指发射机系统在各类噪声的作用下引起的输出信号的相位产生的随机变化。相位噪声可由高频振荡器、功放等发射机器件引起。
理论上辐射源发射的信号为:
s(t)=Aej(2πfct+θn+φ0),
(1)
式中,A为信号幅度;fc为载波频率;θn和φ0分别为信号相位和初始相位。
以相位噪声建模辐射源个体差异,则实际的发射信号为:
x(t)=Aej(2πfct+θn+φ0+Δφ(t)),
(2)
式中,Δφ(t)为信号的相位噪声,表达式为:
(3)
式中,Mf为调相系数;fm为随机正弦波的频率。
1.2 非线性特性
在辐射源发射机中,功率放大器作为重要的元器件,起着放大信号功率的作用。理想条件下,功率放大器的增益保持不变。然而,由于制造工艺的限制以及长期使用下的损耗,即使同型号、同批次的功率放大器,其增益也存在差异。不同辐射源个体非线性特性存在的差异,为信号添加了“指纹特征”。目前,针对窄带非理想功率放大器的建模方式主要有Taylor级数模型、Rapp模型和Basel模型等,其中Taylor级数模型应用最为广泛,当功率放大器的非线性较弱时,应用Taylor级数模型建模更能表征功放的非线性特性。Taylor级数模型的表达式为:
(4)
式中,x(t)为输入信号;y(t)为输出信号;an为功放Taylor级数模型的第n阶参数,an的不同直接导致了不同功率放大器的非线性差异。
2 相关理论
2.1 VMD
VMD是在变分问题的整体框架下,最终将原始信号f(x)分解成K个中心频率不同的IMF的自适应分解方法[19]。
首先,定义每个IMF为调频-调幅(FM-AM)信号,表达式为:
uk(t)=Ak(t)cos(φk(t)),
(5)
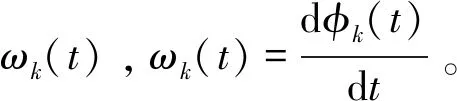
(6)
式中,ωk为各IMF的中心频率,k=1,2,…,K。
为求解最优解,将约束性变分问题转化为非约束性变分问题引入二次惩罚因子α和拉格朗日乘数算子λ,得到增广的拉格朗日函数:

(7)
VMD算法运算步骤如下:

步骤2:n=n+1,更新uk,ωk,从1循环至K,
(8)
(9)
式中,ω为频率。
步骤3:更新λ
(10)
式中,σ为保真度系数。
步骤4:满足
(11)
时,迭代终止,其中ε为判别精度。
2.2 RCMDE
在信息论领域,熵是由香农提出的用于检测时间序列动态特征的强大工具[20]。近似熵、样本熵、模糊熵、排列熵和散布熵等特征被广泛应用于信号分类和故障检测等领域[21-25]。但是,上述特征均为单一尺度提取获得,不能完全反映序列性质。因此,多尺度分析方法越来越受到研究者的关注。常用的多尺度模糊熵(Multi-scale Fuzzy Entropy,MFE)往往会忽略各尺度时间序列的相互关系而不能准确地表征原信号,MSE及MPE存在计算复杂度高和耗时较长的问题。相较于其他多尺度熵,Azami等人[16]在散布熵的基础上提出的RCMDE计算更为迅速,更适合分析长时间序列。求解RCMDE的步骤如下:
步骤1:将待分析时间序列设为uk,长度为Ψ,对uk进行粗粒化操作,得到的第h个粗粒度近似信号为
(12)

步骤2:将粗粒度近似信号a={a1,a2,…,aN}通过正态分布函数映射为b={b1,b2,…,bN},
(13)
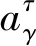
步骤3:将b以线性变换的形式映射到{1,2,…,c},记为z,即,
(14)
式中,R()为取整运算;c为类别个数。
步骤4:嵌入维数为m,时间延迟为d。时间序列定义为
(15)
式中,i={1,2,…,N-(m-1)d}。
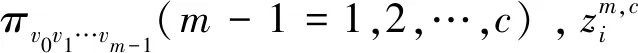
步骤6:计算每种散布模式πv0v1…vm-1的概率P(πv0v1…vm-1),表达式为
(16)

步骤7:对于各尺度下的τ,RCMDE的定义如下
(17)

3 实验仿真与分析
3.1 仿真数据
利用相位噪声及功放非线性特性建模辐射源个体差异,实验所用的信号数据均由计算机软件仿真得到。辐射源信号参数如表1所示。各辐射源的相位噪声和功放非线性特性参数如表2所示。单个信噪比下单个发射机产生的样本个数为50。
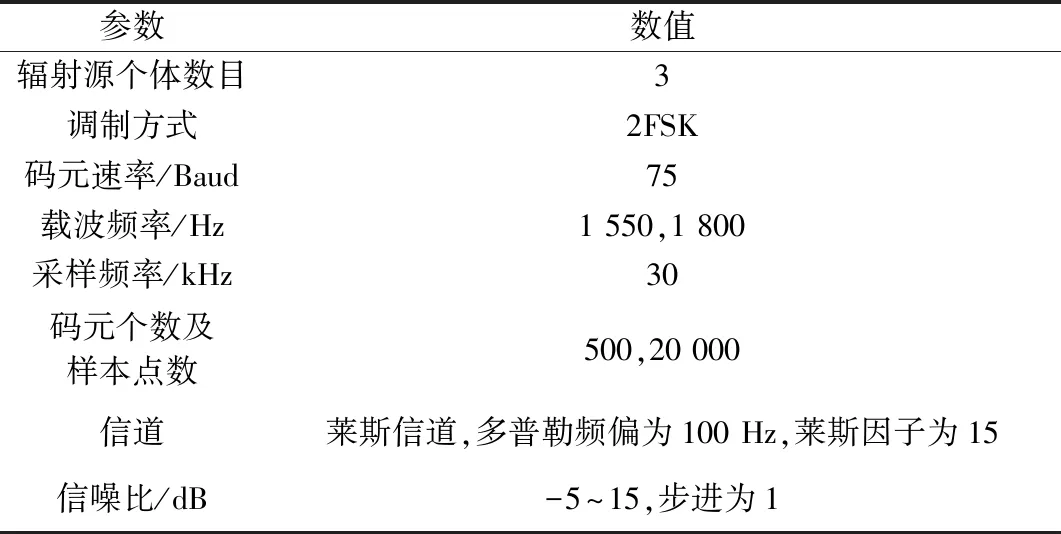
表1 辐射源信号参数Tab.1 Parameters of signal of radiation source

表2 各辐射源的相位噪声和功放非线性特性参数Tab.2 Phase noise and non-linear characteristic parameters of each radiation source
10 dB时,选取3个辐射源个体的某一样本,分别绘制其时域、频域波形,如图2和图3所示。可知,3个辐射源个体发出的信号的包络整体上较为接近,但仍然存在细微差异;3个辐射源发射信号的中心频率一致,其他频率下的幅值有细微差异。

(a) 个体1时域波形

(a) 个体1频域波形
3.2 模态分解
在对信号进行VMD分解前须确定分解的层次数KVMD。KVMD值过小会造成信号的欠分解,不能提取到原始信号的最有效信息;而KVMD值过大往往会引发模态混叠现象,影响分类效果。因此,随机选取某一信号样本,对其进行分解,通过实验,不同KVMD值下各IMF的中心频率如表3所示。
由表3可以看出,当KVMD<6时,分解得到的模态分量未能提取到主要的频率成分;KVMD=6时,主要的频率成分1 550,1 800 Hz均被提取出。因此,本文选取的KVMD值为6。KVMD为6时,随机选择个体1的某一信号,对其进行分解后各IMF的时域信号波形及频谱如图4所示。

表3 不同KVMD值下各IMF的中心频率Tab.3 The center frequency of each modal component under different KVMD values 单位:Hz
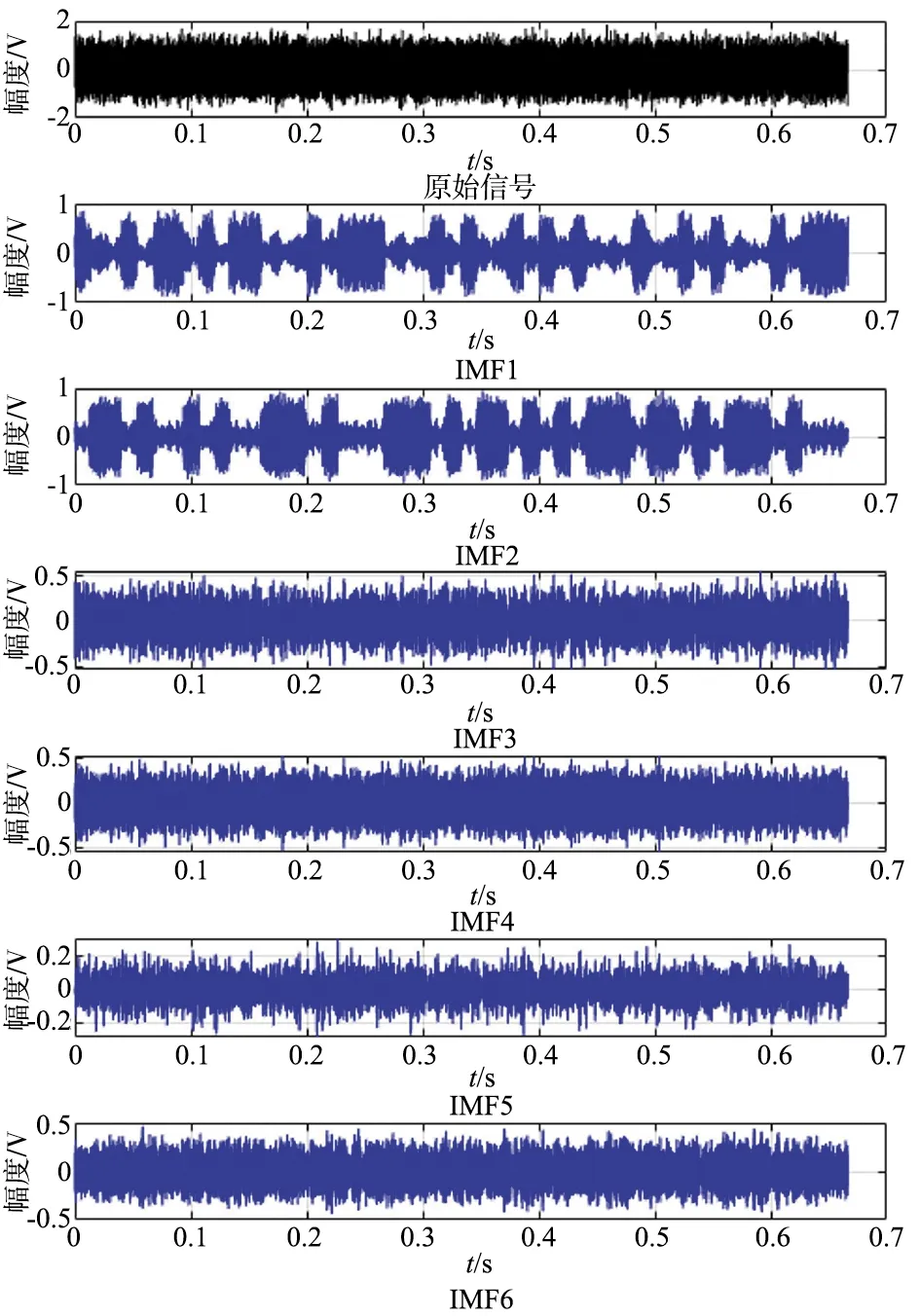
(a) 原始信号和各IMF的时域波形
随后,计算各IMF与原信号的相关系数ri,如图5所示。IMF1~IMF6与原始信号的相关程度均较高,剔除任何IMF都会造成较多有效信息的损失。因此,本文选择保留所有分量。KVMD设置为6时,对维度为1×20 000的原始时域信号序列进行VMD分解,最终得到维度为6×20 000的IMF矩阵。

图5 各IMF与原信号的相关系数Fig.5 Correlation coefficient of each IMF and the original signal
3.3 特征提取
本文对6个有效IMF分量分别提取RCMDE,MPE,MFE等多尺度特征。由式(12)~式(17)可知,计算RCMDE需要分别设置类别个数c、嵌入维度m、时间延迟d和尺度因子τ。MPE,MFE的计算同样需要设置m,d,τ。c,d的设置一般依从过往研究的经验。根据文献[16]的建议,本文将c设置为6,m设置为4,d设置为1。由于τ的设置直接决定特征的维度、耗时以及识别准确率,本节改变τ的取值,分别计算各IMF在不同τ值下的RCMDE,MFE,MPE,MSE等特征,随后对比计算耗时并将特征分别输入至支持向量机(SVM)中比较分类识别性能,SVM最优参数通过网格搜索获得。不同τ值下,计算长度为20 000的IMF的RCMDE,MDE,MSE,MPE的耗时如表4所示。可知,MSE的计算耗时最长,计算耗时是其他特征计算耗时的10倍以上;MDE,MPE,RCMDE的计算耗时差距较小,均为1.10 s左右。

表4 各熵特征计算耗时Tab.4 Calculation time of different entropy feature 单位:s
在相同计算机配置、使用相同软件条件下,不同τ值,RCMDE,MDE,MSE,MPE输入至SVM中的识别准确率如图所6示。由图6可知,不论使用何种特征,识别准确率基本随τ值增大而增大。此外,当1≤τ≤6时,在4种特征中,RCMDE的识别准确率均优于其他特征;τ=6时,RCMDE的识别准确率达到了99.237 6%,达到了最高值。
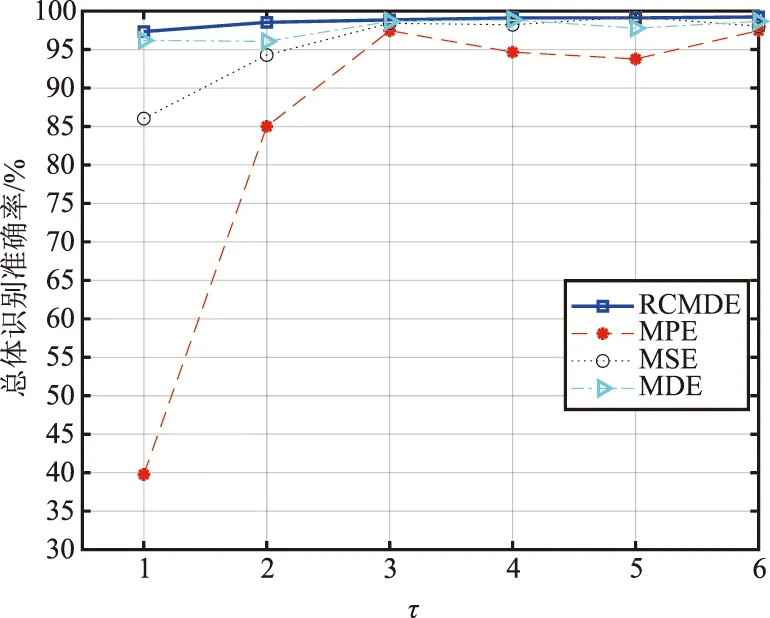
图6 不同τ值下不同特征输入至SVM的识别准确率Fig.6 Recognition accuracy of different features input to the SVM under different τ
在权衡计算耗时和识别准确率后,最终选择RCMDE作为识别特征,其中τ设置为6,特征重构后的维度为1×36。
3.4 分类器选择
在确定将维度为1×36的RCMDE矩阵作为特征向量后,按照1∶1划分训练集和测试集,将训练集分别输入AdaBoosting、GaussianNB、Gradient Boosting(GDBT)、 KNN、多层感知器(Multi-Layer Perceptron,MLP )、随机森林(Random Forest,RF)、SVM等机器学习常用分类器,在参数寻优过程中采用网格搜索法及5折交叉验证,得到最优参数分类器后将测试集样本输入,得到识别结果并对比各分类器识别准确率。分类器参数确定后,不同机器学习方法500次蒙特卡罗实验的平均识别准确率如图7所示。

图7 500次蒙特卡罗实验下不同机器学习方法的识别准确率Fig.7 Recognition accuracy of different machine learning methods under 500 Monte Carlo experiments
在所选取的7种机器学习分类算法中,AdaBoosting及GaussianNB算法的分类效果远远低于其他算法;MLP,GBDT,SVM,RF的识别准确率均超过了99%。各机器学习算法在样本规模均为3 150时进行500次蒙特卡罗实验的耗时如表5所示。其中,GBDT,AdaBoosting以及MLP进行500次蒙特卡罗实验的时间均超过了270 s,远远高于其他方法。此外,GaussianNB方法耗时最短,为3.597 9 s,但是该方法识别性能较一般。RF,SVM以及KNN计算耗时较为接近,且三者识别性能均超过99%,识别性能差距微小。综合识别性能及计算耗时表现,本文选择SVM作为识别算法。
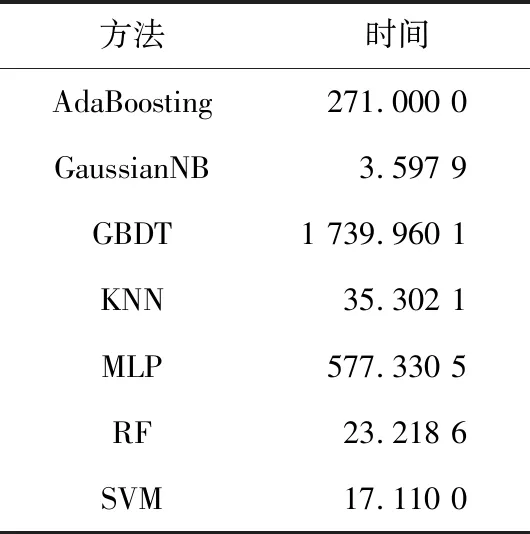
表5 不同机器学习方法的计算耗时Tab.5 Calculation time of different machine learning methods
3.5 对比实验
实验1 不同样本个数下的识别性能分析
在机器学习领域,部分方法受样本个数的影响较大,在样本量过小的时候会出现性能严重下滑的情况。本部分在其他条件不变的情况下,改变样本个数,对比识别性能,分析本文方法在小样本条件下的性能和鲁棒性。原有的样本个数为3 150,将样本个数设置为原有样本个数的10%~90%,间隔为10%。训练集和测试集的比例为1∶1,SVM分类器的参数为3.4节寻优后得到的数值。不同样本个数下的识别准确率如图8所示。由图8可知,当样本个数提升时,识别的准确程度随之上升,当样本个数达到1 890时,识别准确率超过了98.9%。样本个数为315时,识别准确率达到了97.46%。这说明本文方法在小样本条件下仍能保持较高的识别准确率。

图8 不同样本个数下的识别准确率Fig.8 Recognition accuracy under different sample numbers
实验2 不同训练集占比下的识别性能分析
在本实验中,将样本个数设定为3 150,改变训练集样本占全体样本个数的比例,训练集占比10%~90%,间隔为10%。SVM分类器的参数为3.4节寻优后得到的数值。在经过500次蒙特卡罗实验后,得到不同训练集占比下的识别准确率,如图9所示。由图9可以看出,识别准确率总体上随着训练集占比的提高而提升,在训练集占比超过50%后,识别准确率超过了99.2%,此后,训练集占比的提高也不会带来明显的性能提升。此外,当训练集占比为10%时,识别准确率为97.46%,这表明本文提出的方法在训练集占比较低时也有较好的识别性能。

图9 不同训练集占比下的识别准确率Fig.9 Recognition accuracy under different proportions of the training sets
实验3 与其他文献方法的对比
将本文方法命名为VMD-RCMDE,在同等的实验条件下,与文献[26]提出的VMD-LZC方法、文献[14]提出的VMD-SE-PE方法以及文献[15]提出的VMD-MPE-PCA方法进行对比。LZC 指代Lempel-Ziv 复杂度。训练集占比为50%。本文方法与其他文献方法的识别性能及不同信噪比下的识别准确率如图10和图11所示;不同方法在样本规模均为3 150时进行500次蒙特卡罗实验的耗时如表6所示。

图10 本文方法与其他文献方法的识别性能Fig.10 Recognition performances compared with other literature methods

图11 不同方法在不同信噪比下的识别准确率Fig.11 Recognition accuracy of different methods under different SNRs
由图10和图11可知,在-5~15 dB的信噪比范围内,VMD-RCMDE方法总体识别性能优于其他文献方法,500次蒙特卡罗实验的平均识别准确率达到了99.237 6%;信噪比为-5 dB时,识别准确率达到了93.7%,较其他方法高27%以上;信噪比在-1 dB及以上时,识别准确率达到了100%。此外,VMD与熵复杂度特征结合的方法识别性能优于VMD-LZC方法,这说明熵特征在挖掘个体指纹特征上更具有优势。在上述VMD与熵复杂度特征结合的方法中,VMD-RCMDE性能最优,这是由于RCMDE从多尺度进行特征提取后得到的指纹特征更为细腻丰富。同时,不对RCMDE进行降维操作保留了全部的有效信息,避免了识别性能的下滑。由表6可知,在同等样本规模下进行500次蒙特卡罗实验,VMD-RCMDE方法耗时17.110 0 s,远低于其他方法,这说明该方法不仅提升了识别准确率,还使耗时大为降低。
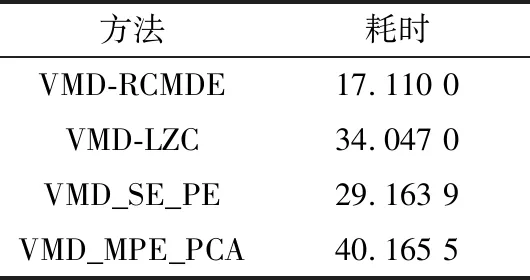
表6 不同方法同等样本规模下500次蒙特卡罗实验的耗时Tab.6 Calculation time of 500 Monte Carlo experiments with different sample sizes 单位:s
4 结束语
针对用于SEI的典型一维特征常常引发识别性能下滑,高维度特征维度较大、与一般分类器结合使用时计算效率较低等问题,本文提出了一种基于VMD和RCMDE的SEI方法。仿真结果表明,当信噪比在-5~15 dB时,以IMF的RCMDE为输入的SVM的识别准确率达到99.237 6%。通过实验,验证了所提出的方法在样本个数、训练集占比等变化时仍具有较强的鲁棒性。最后,与其他SEI方法相比,所提出的方法在识别性能上更优、耗时更短。

