对高中物理沿绳方向加速度关系的探讨
邓 伟
(重庆市开州中学 405499)
1 一道高三复习题的思考
在高中物理教学过程中,笔者遇到一个很有争议的题目,题目如下:
例1如图1所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.现将环从与定滑轮等高的A处由静止释放,当环沿直杆下滑距离也为d时(图中B处),下列说法正确的是(重力加速度为g)( ).
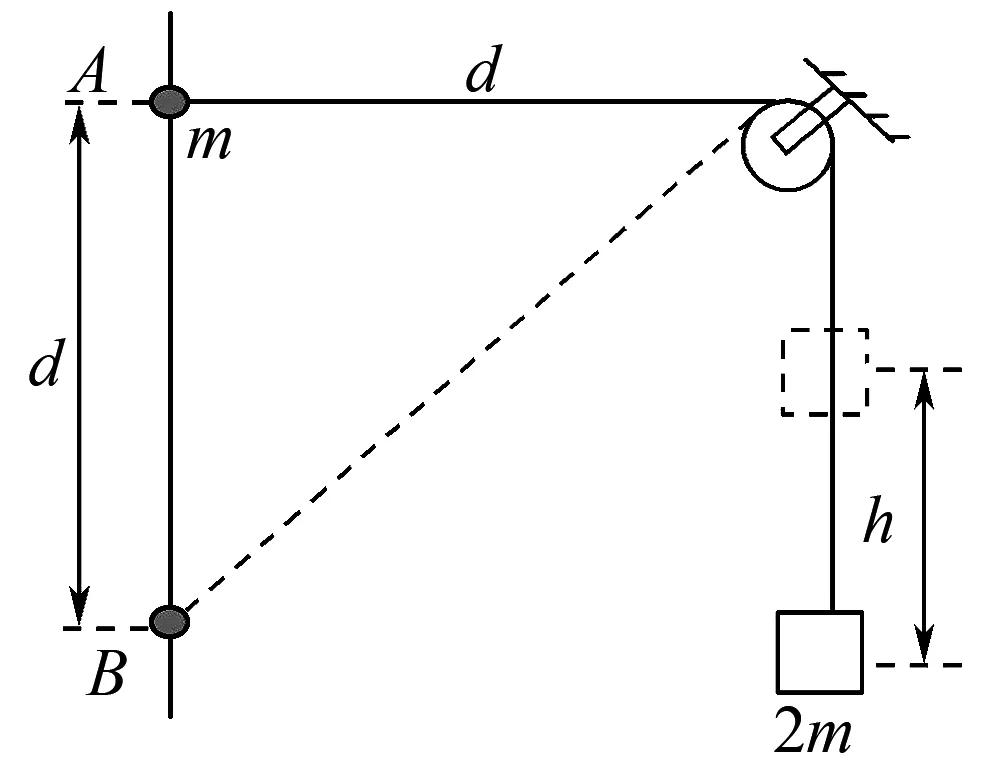
图1
A.环刚释放时轻绳中的张力等于2mg
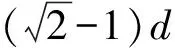
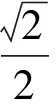
D.环减少的机械能大于重物增加的机械能
原参考答案:B.
解析环刚开始释放后,重物由静止开始加速上升,故重物有向上的加速度,根据牛顿第二定律有F-2mg=2ma,得F>2mg,得,故A项错误;
通过与老师的研讨中也发现有的认为A为正确答案,解答如下:环刚开始释放时,环的加速度为g,通过沿绳子方向加速度相等,得到重物在瞬间加速度为0,则绳子的张力F=2mg,故A正确.那究竟哪种说法是正确的呢?
2 沿绳子方向加速度关系与速度关系是否相同
假设我们认为两者关系是一致的,以例1为例,设环到B点的加速度向下为aB,此时绳子与杆的夹角为θ,如果我们类比速度之间的关系,可以得到重物加速度a物=aBcosθ.我们用特例进行反证:如果环在外力作用下保持匀速下落,则aB=0,从加速度关系可得,重物上升加速度a物=aB=0,说明重物也是匀速上升.但从速度关联的角度,当环匀速下落时,因为两者速度满足v物=vBcosθ,当环下落过程中,角度θ越来越小,利用余弦函数单调递减得出重物上升速度是越来越大的,说明重物的加速度竖直向上不为0.两个结论产生了矛盾,说明假设是错误的:沿着绳子方向加速度关系与沿绳子方向速度关系不一定相同.
3 沿绳子方向加速度关系的推导
同样借助例1,我们用数学方法来推导:
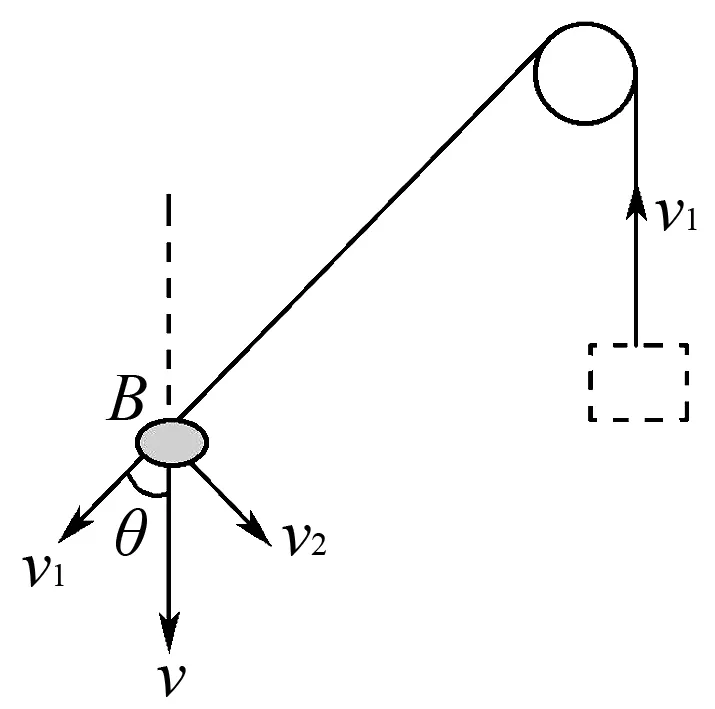
图2
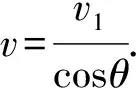
[f(g(t))]′=f′(g(t))·g′(t)得:
①
②
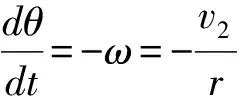
③
(其中r为此时环到滑轮与绳的接触点(后面简称接触点)之间的绳长、v2是环沿着接触点转动的线速度,角度θ随时间增加而减小,所以有负号).
④
将②式、③式和④式代入①式得:
⑤
⑥
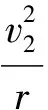
综上分析,我们可以得出结论:环的加速度沿绳子的分量等于重物上升加速度(左端绳子伸长的加速度)与环绕点转动的向心加速度矢量和.
4 高中范围内,哪些情况物体沿绳子方向加速度相等?
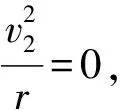
4.1 绳子两侧的物体速度方向与连接的绳子平行,都做直线运动,不存在绕点转动.
例2如图3所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为4m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计.开始时整个系统处于静止状态;释放A后,A沿斜面下滑至速度最大时,C恰好离开地面.求:斜面的倾角α;
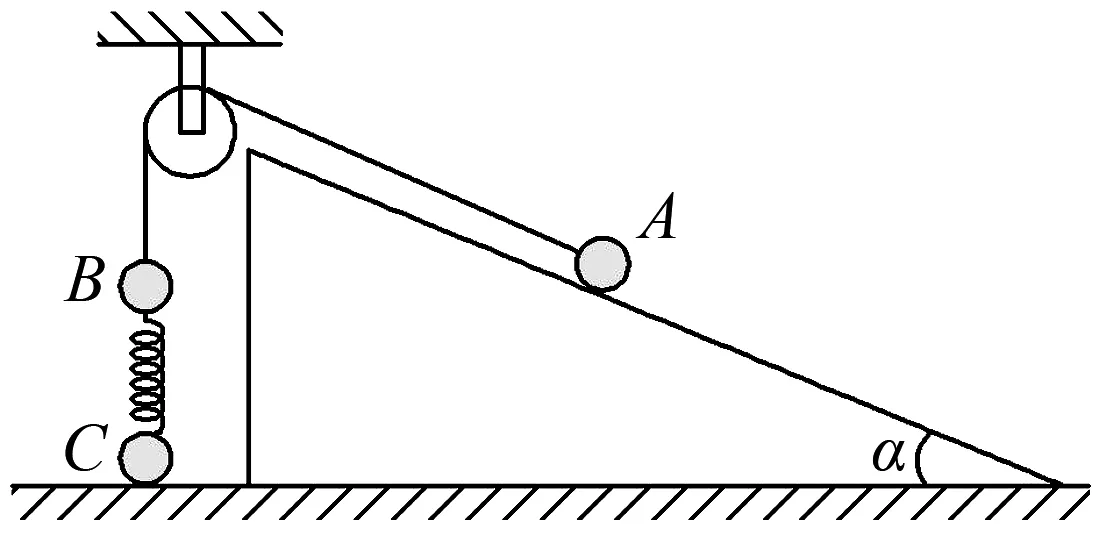
图3
解析由题意可知,当A沿斜面下滑至速度最大时,C恰好离开地面,C的加速度为0;AB加速度时刻相等,此时为零.将ABC作为一个整体:
由牛顿第二定律得4mgsinα-2mg=0,
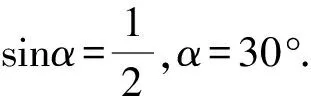
4.2 物体做圆周运动等存在绕点转动的情况,但速度为0
物体即使存在绕点转动的情况,如果速度为0,向心加速度也为0,所以沿绳子方向的加速度仍然相同,这些情况一般出现在开始运动时或运动结束时.在2018年江苏卷中,直接涉及到沿绳子方向加速度相等结论的应用.
例3(2018江苏卷14题)如图4所示,钉子A、B相距5l,处于同一高度.细线的一端系有质量为M的小物块,另一端绕过A固定于B.质量为m的小球固定在细线上C点,B、C间的线长为3l.用手竖直向下拉住小球,使小球和物块都静止,此时BC与水平方向的夹角为53°.松手后,小球运动到与A、B相同高度时的速度恰好为零,然后向下运动.忽略一切摩擦,重力加速度为g,取sin53°=0.8,cos53°=0.6.求:
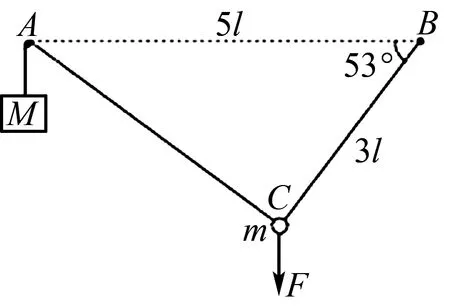
图4
(1)小球受到手的拉力大小F;
(2)物块和小球的质量之比M∶m;
(3)小球向下运动到最低点时,物块M所受的拉力大小T.
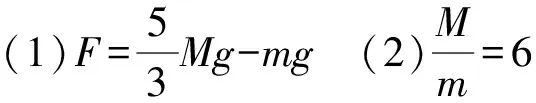
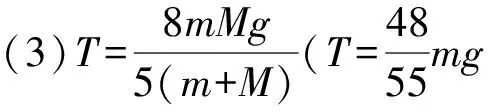
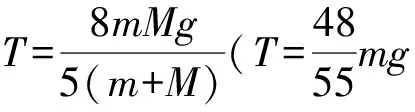
5 综述
通过对本问题的探讨,笔者获得如下结论:连接体沿绳方向加速度的关系与速度间的关系不一定相同.我们既要考虑平动的加速度,也要考虑转动时的向心加速度.在高中物理学习中,下列情况的加速度之间的关系和速度关系是相同的:1.绳子两侧的物体速度方向与连接的绳子平行,都做直线运动,不存在绕点转动的情况.2.物体做圆周运动存在绕点转动时,但速度为0的情况.

