Design optimization of broadband extreme ultraviolet polarizer in high-dimensional objective space

Shang-Qi Kuang(匡尚奇)， Bo-Chao Li(李博超)， Yi Wang(王依)，Xue-Peng Gong(龚学鹏)，‡， and Jing-Quan Lin(林景全)，§

1School of Science，Changchun University of Science and Technology，Changchun 130022，China

2Key Laboratory of Ultrafast and Extreme Ultraviolet Optics，Changchun University of Science and Technology，Changchun 130022，China

3State Key Laboratory of Applied Optics，Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China

Keywords: extreme ultraviolet polarizer，multilayer design，multi-objective genetic algorithm

1. Introduction

Recently， because extreme ultraviolet lithography(EUVL) is becoming the predominant technology for high volume manufacturing of semiconductor device， the production of EUV mirrors coated by Mo/Si multilayers has become a critical technique in EUVL.[1]The throughput of EUVL strongly depends on reflection spectra of multilayer coating and integration result of multilayer spectra. Therefore，a mass volume accurate reflectance measurements of Mo/Si multilayers are important for the production of EUVL systems， and then the EUV reflectometer should be essential.[2–4]For an accurate reflectometry， a polarizer with broadband and flattop reflection spectrum is required，[5]and the related works have attracted much attention of many research centers around the world， presumably due to pursuance of polarization measurements with the use of synchrotron radiation.[6]In order to increase the reflected bandwidth， the non-periodic multilayer structure has been used，thus multilayer design is the key step in the broadband polarizer development.[7，8]We realize this multilayer design is an issue of multi-objective optimization，which requires to simultaneously optimize the reflectivity throughput，polarization degree and flatness of reflectivity profile. Furthermore，the layer thickness fluctuation is inevitable in the multilayer fabrication process， and the broadband reflectivity is sensitive to the layer thickness errors，[9，10]thus the robust multilayer design must be an additional objective.As a result，the comprehensive design of EUV broadband polarizer requires the optimizations of four targets. Meanwhile，it is worth pointing out that multi-objective optimization is a quite common requirement in the designs of EUV multilayers，such as EUV broadband mirror，[11，12]EUV beam splitter，[13]and EUV chirped mirror.[14]Therefore， the multi-objective optimization is a fundamental issue to be addressed for the development of EUV optics.

Until now，the traditional method of EUV multilayer design is to convert all objectives into a single goal by optimizing the summation of different merit functions，[10，12，15]and presetting the aimed reflectivity as a constant， it is hard for this method to disclose the relations between objectives，and sometimes it is even impossible to supply a proper weight between the objectives and explore the potential ability of the multilayer system. Furthermore， an advanced optimization technique is very important for the design of multilayered coating in other wavelength range，[16]and multi-objective optimization is also needed in the designs of optical coatings.[17，18]Most recently， we introduced the multi-objective genetic algorithms(MOGA)in the design and fabrication of broadband EUV multilayer，[19，20]but the basic MOGA can not go forward to find optimal solutions when encountering a task with more than three objectives， especially many parameters need to be optimized.

In the last decade，a lot of different MOGAs had been supplied and performed well on optimizing many objectives.[21]Because the targets usually are conflicting， the optimization based on MOGA generates a set of solutions representing the best possible trade-offs， which form the Pareto-optimal set， and its distribution in the solution space is defined as Pareto-optimal front. Furthermore，in order to solve the manyobjectives problem and obtain an unique solution efficiently，the MOGA using a reference direction has also been developed in soft computing.[22]In this paper， the MOGA was improved to design the broadband EUV polarizer with four objectives， and MOGA with reference direction (MOGAANGLE) was developed to search the desired regions in the 4D solution space. In theory，the optimal EUV multilayer designs have been obtained，and this research has demonstrated that our method has a great potential application in the designs of optical thin films.

2. Theoretical design of EUV broadband polarizer based on MOGAs

2.1. Mathematical modeling of EUV multilayer polarizer

The transfer matrix method is very suitable to calculate the reflectivity of multilayer system，and we used it to calculate the propagation of electromagnetic wave in the non-periodic multilayer stack. In the multilayer system，the continuity condition and conservation of wave propagation in the direction perpendicular to the multilayer are considered，and the propagation of wave in a homogeneous layerjwith a thicknessdjin the multilayer stack can be characterized by a transfer matrixMj，and this matrix which connects the electric field between the layersjandj+1 can be given by

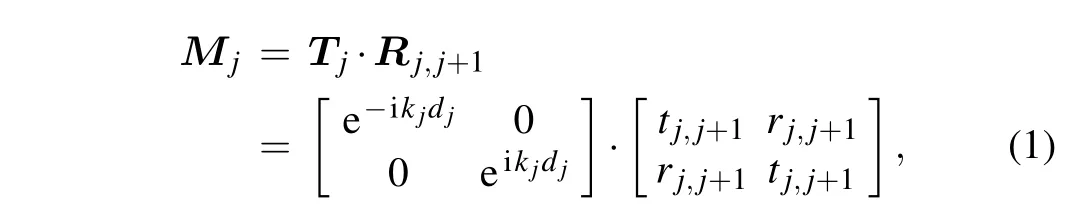
whereTjandRj，j+1are the translation and refraction matrices，respectively. Meanwhile，the Fresnel reflection and transmission coefficients can be written as

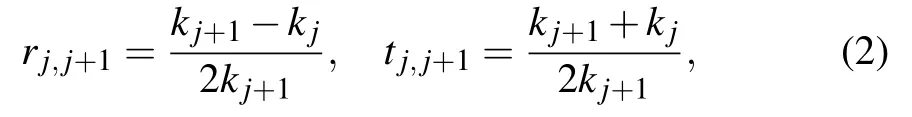
wherekjandkj+1represent thez-components of the wavevectors for layersjandj+1， respectively. For the different polarization of the incident wave，the value ofkjcan be given by

whereλis the wavelength of plane wave andθjis the incident angle of the layerj. Here ˜nj=1-αj-iβjrepresents the complex refractive index of layerj， and the optical constants are obtained from CXRO database.[23]In an actual multilayer，the reflectivity is very sensitive to interfacial roughness，so we consider this effect in the simulation，and the Fresnel reflection coefficientrj，j+1should be modified by[24]

whereσj，j+1is the interfacial roughness between the layersjandj+1. We assume the multilayer stack containsnlayers，and the electric field amplitude on the surface of multilayer mirror can be obtained by multiplying all the refraction and translation matrices in each layer starting from the substrate

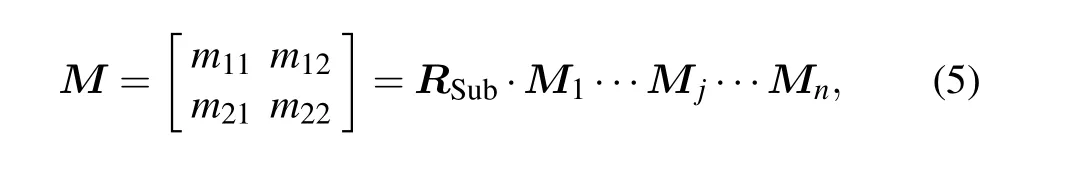
whereRSubrepresents the reflection matrix between the substrate and the first layer. At the surface of multilayer system，the Fresnel reflection coefficient of the electric field can be given by

and then the reflectivity of multilayer stack can be given by

For a multilayer polarizer in the range of EUV wavelengths， the incidence angle of reflected multilayer is set to be quasi-Brewster angle，where the reflectivity of p-polarized radiation is at a minimum， and its degree of polarization is defined by

whereRsandRpare the reflectivities for s- and p-polarized radiations，respectively.

2.2. Multilayer design of EUV polarizer based on improved MOGA

The design optimization of reflected EUV multilayer polarizer having a wide wavelength bandpass is very representative，which needs to meet many requirements such as reflectivity throughput，polarization degree，flatness and stability of the reflectivity profile. Therefore， the corresponding merit functions of these performances can be written as

where the first merit functionf1is the reciprocal of reflected throughput， and ¯Rsis the average reflectivity for the s-polarized radiation. Meanwhile，λmin=12.5 nm andλmax=15.0 nm are the minimum and maximum wavelengths，respectively.[4]The second merit functionf2characterizes the deviation of calculated reflectivity profile for s-polarized radiation from its average reflectivity. The third merit functionf3means the proportion of p-polarized radiation，thus the minimization of this merit function can lead to an enhancement of reflected s-polarization degree. The fourth merit functionf4characterizes the sensitivity of reflectivity profile for s-polarized radiation to the random thickness errors of all the layers，[25]anddiandδiare the thickness and thickness error’s standard deviation of theith layer，respectively. We assumemlayers contained in the multilayer system should be optimized，and these layers have the thickness errors which originate from imprecision deposited control of quartz crystal monitoring or time monitoring. Therefore， the layer thickness errors of individual layers are non-correlated， which distribute in accordance with the normal law with zero mathematical expectation and a given standard deviation. These four performances of multilayer can be optimized by the minimization of functions in Eq.(9)，and we set them as optimized targets of MOGA.

The MOGA used in the multilayer optimization is based on the evolutionary algorithm named as nondominated sorting genetic algorithm II (NSGA-II)，[26]where the gene of each individual in the population is characterized by a set of parameters which are the layer thicknesses of the multilayer system.For searching the solutions in the 4D objective space， several improvements have been made for NSGA-II. It is found that the operation of crowding distance is a good choice of remaining the diversity of population when the number of optimized targets is no more than three， and this is the reason why NSGA-II becomes the representative of state-of-the-art MOGAs. However，for dealing the optimization with four objectives， we at first adopt the archive truncation method from SPEA2[27]in the archive update process，that is，if the number of nondominated solutions is larger than the population sizeN，theNleast-crowed nondominated solutions based on their Euclidean distances to the nearest neighbor are kept， and this way can somehow enhance the diversity of population. Secondly， we use a larger population sizeN=200 and run the program until 20000 generations， which can lead to an effective searching，and the distribution index of mutationηm=1，distribution index of crossoverηc=1， crossover probabilitypc=1，and mutation probabilitypm=1/mare used. Thirdly，we add a penalty function in evaluating values of merit functions for each individual，that is，if the value of merit functionf1＞1.25 orf2＞0.00075，all its values of merit functions are revalued byfi+β(i=1，2，3，4)，whereβ=106.This strategy can exclude the individual whose average reflectivity is lower than 32%or average deviation between the calculated and average reflectivities is larger than 2.0%，and then we can search the multilayer designs in the solution region where all the solutions meet the basic requirements of EUV polarizer. Although the calculation of our multilayer design method is somewhat larger， this evolutionary algorithm is very suitable for parallelization at multi-core and multi-processor high-performance computing systems.

2.3. Multilayer design of EUV polarizer based on developed MOGA-ANGLE

Although the multilayer design optimization based on MOGA can supply a series of representative efficient solutions， the limited nondominated solutions are difficult to go forward the Pareto-optimal front and they are impossible to distribute over the whole solution space. Therefore，we introduce the angle-based preference selection mechanism[22]into NSGA-II，where the angle assigned to each individual belonging to the set of Pareto-equivalent solutions is considered as the second selection criterion during the evolutionary process.In the operation of angle-based preference selection mechanism，the original point in the solution space is set as the aspiration point， and then for a desired solution (f1r，f2r，f3r，f4r)in the solution space，the searching direction can be defined asFr=[f1r，f2r，f3r，f4r]. In the same way， for each individualjin the population， a vectorFj=[f1j，f2j，f3j，f4j]is formed by connecting it with the original point，and then the angle between this vector and the desired searching direction can be calculated by[22]

Because the procedures and parameters of MOGA and MOGA-ANGLE are nearly the same，both algorithms are consistent. As a result，our approach not only supplies a stronger selection pressure but also takes advantage of the preference information of nondominated solutions supplied by MOGA to guide the further search toward the desired region.

3. Results and discussion

3.1. Global optimization of EUV multilayer polarizer using MOGA

In this research， we consider the design of Mo/Si multilayer used for reflective polarizer， and the incident angle is set to be Brewster angle of 42.5°.[4]In the realistic Mo/Si multilayer system， the reflectivity is sensitive to the imperfections of interface， interlayers and oxidation of the top layer， thus we consider all these effects in our simulations.It is a good assumption that the two interlayers have the same chemical composition of MoSi2and fixed layer thicknesses， and the certain multilayer system can be defined as Sub/[MoSi2/Mo/MoSi2/Si]49/SiO2，[7，11]which can be a good example for the multilayer design. Here the SiO2oxide layer results from the oxidation of top silicon layer with a thickness of 2 nm and a surface roughness of 0.5 nm r.m.s. Furthermore， the densities of all materials in the layered system are assumed as their bulk densities and the interfacial roughness is 0.3 nm r.m.s. Therefore，this layered system can be a suitable model for the Mo/Si multilayer deposited by DC magnetron sputtering.[7，28]We optimize the thicknesses of Mo and Si layers in the multilayer system，and assume the random thickness errors of these layers having a normal distribution with a standard deviation of 0.05 nm.

According to different generations，the nondominated solutions of MOGA are demonstrated in Fig. 1. Because the population evolves in the 4D solution space， we present the nondominated solutions in two 3D maps，where the values of merit functionsf1andf3have been converted to mean value of reflectivity for s-polarized radiation and average polarization degree，respectively. An investigation of Fig.1 shows that the nondominated solutions gradually spread in the 4D solution space in the process of evolution.In Fig.1(a)，we focus on the distribution of nondominated solutions of the 20000th generation，it is found that there is a conflicting relation between the average reflectivity and average polarization degree， and the average polarization degree of multilayer can be easily optimized to higher than 99.8%. In Fig.1(b)，one can see that the multilayer design with a flatter reflectivity profile usually can supply a more stable reflectivity with respect to the random layer thickness errors. Because the average reflectivity and reflectivity flatness are the main performances，it is meaningful to achieve two kinds of multilayer designs，one has flattest reflectivity profile，and the other has an acceptable deformation of reflectivity plateau，and both kinds of solutions should have the average reflectivities as high as possible. In the nondominated solutions of the 20000th generation，we chose the solution having smallest value off2，and according to the variation trends of function values off2andf4，we setf2r=10-5andf4r=0.0025 in Eq. (10) to form the desired solution I with the coordinates(0.3364，0.00001，0.9984，0.0025)as shown in Fig. 1. In the same way， we chose the solution with value off2r=0.0005 which characterizes the acceptable deformation of reflectivity profile， and setf1r=1.1 andf4r=0.0035 in Eq. (10) to form the desired solution II with the coordinates(0.3636，0.0005，0.9980，0.0035) as presented in Fig. 1. As a result， both desired solutions are used by MOGA-ANGLE to guide the searchings toward desired solution regions， respectively.

Fig.1. Obtained nondominated solutions according to different generations of MOGA.(a)Nondominated solutions in 3D map with the coordinates of average reflectivity，deformation of reflectivity profile and average polarization degree. (b) Nondominated solutions in 3D map with the coordinates of average reflectivity， deformation of reflectivity profile and sensitivity to random layer thickness errors. Two desired solutions are used to form the searching directions for the optimizations of MOGA-ANGLE.

3.2. Local optimization of EUV multilayer polarizer using MOGA-ANGLE

By using the desired solutions shown in Fig. 1， the obtained nondominated solutions based on MOGA-ANGLE are demonstrated in Fig.2，where the nondominated solutions obtained by MOGA are also presented for a better comparison.In Fig.2，after 20000 generations of MOGA-ANGLE，all the solutions concentrate in a small region，which means the local searching has been realized，and we define the obtained solutions based on desired solutions I and II as designs I and II，respectively. An investigation of Fig. 2 shows that designs I and II localize at regions which are beyond the nondominated solutions obtained by MOGA， thus MOGA-ANGLE can be used to extend the searching region and both solutions should be closer to the Pareto-optimal front. It is found that all the performances of designs I and II are worse than that of desired solutions I and II，respectively，which means the obtained solutions are the feasible ones which are closest to the searching directions.

In order to compare our design method with the traditional method of multilayer design，we derive the EUV multilayer structure based on the genetic algorithm(GA)，[7]and the merit function used can be written as[9，10]

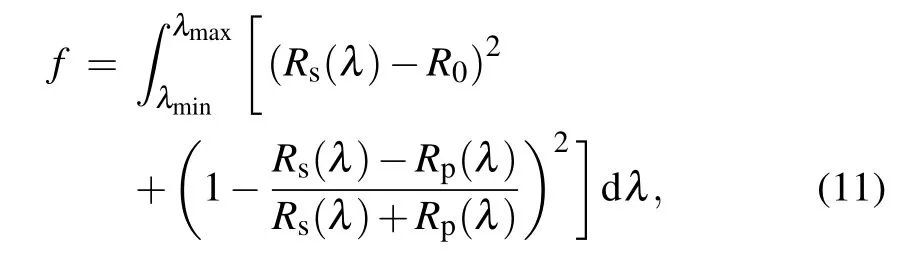
where the aimed reflectivity isR0， and we set its value to 32.5%， 32.7% and 33.0%， respectively. Furthermore， we use the same population size and control parameters of MOGA in the evolutionary process of GA， and then the optimized multilayer design based on Eq. (11) is obtained. Using the optimized multilayer designs based on GA，we calculate the function values in Eq.(9)and demonstrate these solutions， which are named by designs GI， GII and GIII in Fig. 2. Those solutions correspond to the aimed reflectivities of 32.5%，32.7%and 33.0%，respectively. In Fig.2，it is found that the performances of optimized multilayer design strongly depend on the value of aimed reflectivity in the traditional design method，because the aimed reflectivity value of design GII is equal to the preferred value of average reflectivity of design I， the design GII can supply a better reflectivity profile，while the reflectivity profiles of designs GI and GIII have much more fluctuations， and it is very difficult for traditional designing method to obtain this preferred value of aimed reflectivity. The solutions of designs GI and GIII are not beyond the nondominated solutions obtained by MOGA as shown in Fig.2，thus the performances of design GII are better， however， it is found that all the performances of design I are better than that of design GII，and there are three reasons for this result. Firstly，basing on the merit function of Eq. (11)， only the reflectivity profile and polarization degree can be optimized in the process of GA， and it is very difficult to obtain the multilayer design which has a higher average reflectivity than the aimed reflectivity. Secondly， the weight between deviation of calculated profile and proportion of p-polarized radiation is not considered in Eq.(11)，thus the deviation of reflectivity profile which usually has a larger value is mainly optimized， and the average polarization degree can not be fully optimized. Thirdly，one can not obtain the robust design via GA with a single target described by Eq. (11). As a result， our designing method based on MOGA has a higher probability to obtain the optimal multilayer design，where all these performances of multilayer can be optimized simultaneously，and the robust multilayer designs have been obtained.

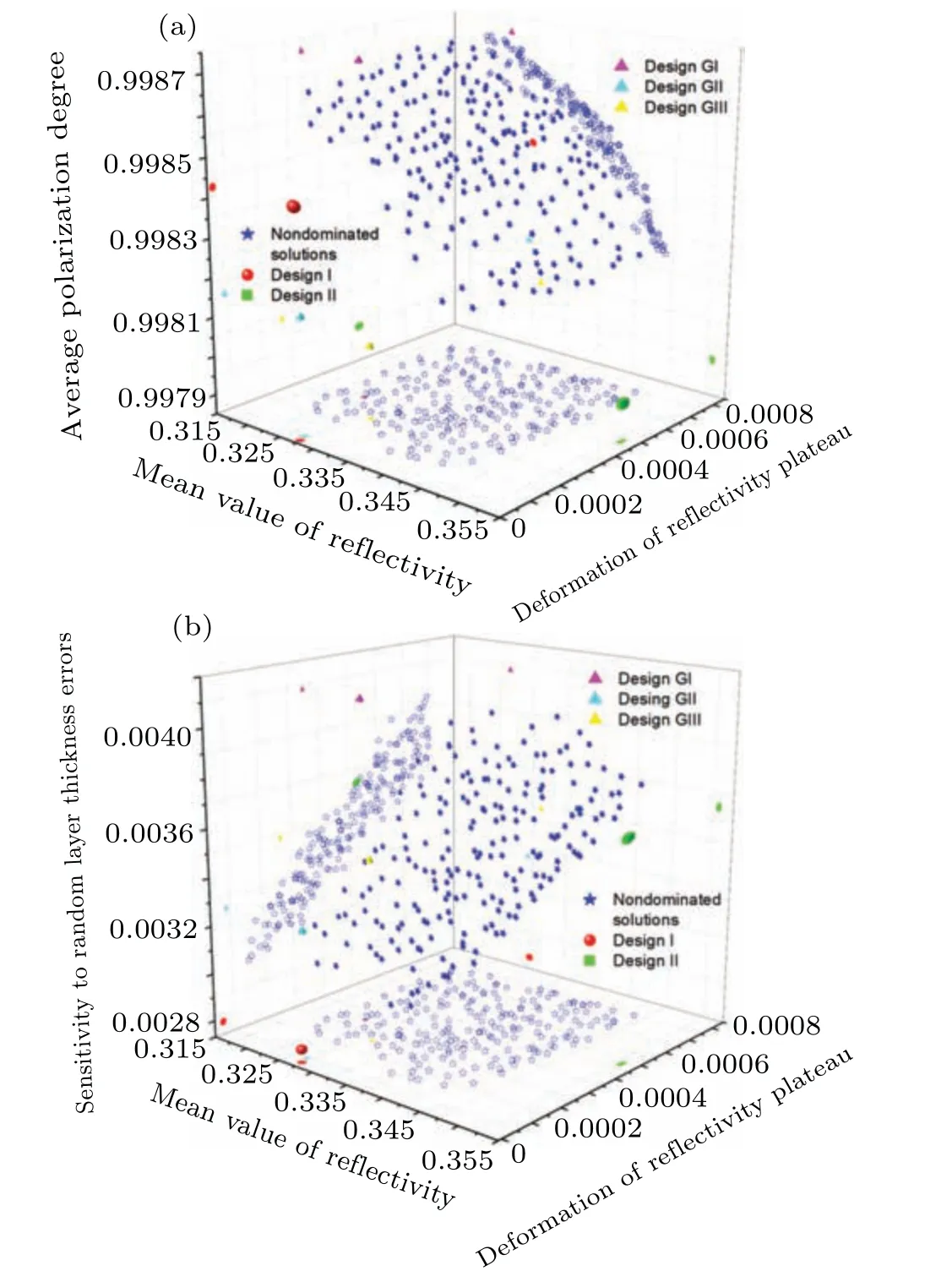
Fig.2. Obtained nondominated solutions of MOGA after 20000 generations，and nondominated solutions obtained by MOGA-ANGLE after 20000 generations according to different desired solutions as shown in Fig.1.(a)Solutions in 3D map with the coordinates of average reflectivity， deformation of reflectivity profile and average polarization degree.(b) Solutions in 3D map with the coordinates of average reflectivity，deformation of reflectivity profile and sensitivity to random layer thickness errors. The designs GI， GII and GIII are the multilayer designs obtained by the conventional design method which is based on genetic algorithm with a single target，and the values of aimed reflectivites are 32.5%，32.7%and 33.0%，respectively.

With the purpose to further compare the EUV multilayer designs as shown in Fig.2，the thickness distributions，reflection spectra for s-polarized radiation and polarization of design I，design II and design GII are respectively demonstrated in Fig. 3. An investigation of Fig. 3(a) shows that the depthdistributions of layer thickness for design I and design GII are quite different， thus our design method is totally different with the traditional design method based on GA. In order to consider the variations of reflectivity profile induced by the random layer thickness errors， the reflectance mathematical expectationRs+MΔRswith standard deviation corridorRs+MΔRs±SΔRscan be calculated by[25，29]

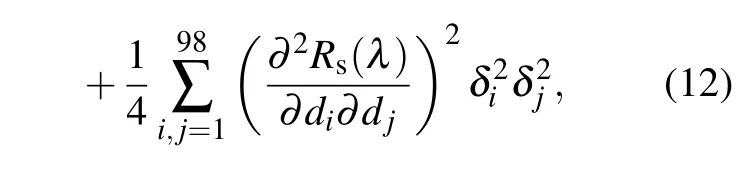
wheredjandδjare thickness and thickness error’s standard deviation of thejth layer， respectively. As a result，the reflectivity profile， average reflectivity， polarization， and reflectance mathematical expectation with standard deviation corridor of design I， design II and design GII are demonstrated in Figs.3(b)，3(c)and 3(d)，respectively. The corridor characterizes possible deviation of reflectance from the calculated curve，which is induced by the layer thickness errors，and a smaller corridor indicates the multilayer design has a lower sensitivity to the random thickness errors. Comparing Figs. 3(b) and 3(c)， it is found that although the average reflectivity of design II is 2.6%higher than that of design I，the flatness，polarization and corridor of design II are much worse than that of design I，thus one can obtain the optimized multilayer design via searching the desired region in the 4D objective space. It is worthwhile to point out that design II is the multilayer structure with the highest average reflectivity and the acceptable fluctuation of the reflectivity profile in the solution space. Comparing Figs.3(b)and 3(d)，one can see that all the performances of design I are better than that of design GII，which are consistent with the results shown in Fig.2，and then we supply a new way to achieving the optimized multilayer design. Owing to the information of nondominated solutions in the solution space， our proposed designing method has a higher probability of achieving the optimal multilayer design.

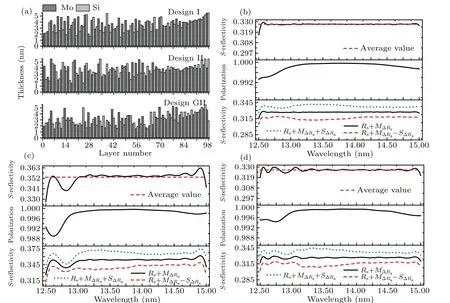
Fig.3. (a)The depth-distributions of layer thickness for the different Mo/Si multilayer structures as defined in Fig.2. The naturally formed interlayers are considered，and the thicknesses of Mo-on-Si and Si-on-Mo interfaces are 1.0 nm and 0.5 nm，respectively，but these interlayers are not presented. The roughnesses of interface and top layer are 0.3 nm r.m.s and 0.5 nm r.m.s，respectively. In(b)，(c)and(d)，the reflectivity for s-polarized radiation (top)， polarization degree (middle) and mathematical expectation Rs+MΔRs and standard deviation corridor Rs+MΔRs±SΔRs of reflected plateau(button)are given according to design I，design II and design GII，respectively.

4. Conclusion

In summary， we theoretically combined the improved MOGA and developed MOGA-ANGLE in the multilayer design of broadband EUV polarizer. The main contribution of the optimization based on MOGA is the globe searching of solutions， which supplies the relations between different objectives and the interesting solution regions. The optimization via MOGA-ANGLE can supply a local search to obtain the further optimized solution，and then both algorithms can complement each other in the multilayer design optimizations.Our researches demonstrate the capability of our method in designing EUV broadband polarizer，and it has a potential to extend to design other optical multilayers， such as EUV broadband mirror，[11，12]EUV beamsplitter，[13]and chirped mirrors.[14，17]

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 62175018， 61905239，and 61974142) and Jilin Scientific and Technological Development Plan， China (Grant Nos. 20190201013JC and 20200401052GX).