Current-driven dynamics of skyrmion bubbles in achiral uniaxial magnets

Yaodong Wu(吴耀东)， Jialiang Jiang(蒋佳良)， and Jin Tang(汤进)2，，†

1School of Physics and Materials Engineering，Hefei Normal University，Hefei 230601，China

2School of Physics and Optoelectronics Engineering Science，Anhui University，Hefei 230601，China

3Anhui Province Key Laboratory of Condensed Matter Physics at Extreme Conditions，High Magnetic Field Laboratory，HFIPS，Chinese Academy of Sciences，Hefei 230031，China

Keywords: skyrmion bubbles，dynamic motion，artificial neural computing

1. Introduction

Skyrmions are promising information carriers applied in future high-performance spintronic devices owing to their particle-like and topological properties.[1–9]Particularly， the easy dynamic manipulations of skyrmions at very small currents predict the potential energy-efficient functional operations in skyrmion-based spintronic devices such as racetrack memory.[10–12]Skyrmions are typically stabilized by chiral Dzyaloshinsky–Moriya interactions in noncentrosymmetric magnets.[1，4]The spin-torque-driven motion dynamics of chiral skyrmions such as velocity and Hall angle have been well constructed in theory and experimentally identified.[13–17]Besides，skyrmions(also called skyrmion bubbles)can be also stabilized by dipole–dipole interactions in centrosymmetric uniaxial magnets.[2，18–26]There are two types of bubbles in centrosymmetric uniaxial magnets，i.e.，type-I skyrmion bubble and type-II topologically-trivial bubble.[24]Because of the absence of chiral interactions， skyrmion bubbles in the centrosymmetric magnets are achiral and have two helictites at a given field.[19，20]Achiral skyrmion bubbles have been found in many room-temperature centrosymmetric ferromagnets， such as Fe3Sn2，[22]Fe/Gd，[20]and BaFeScMgO.[21]The size of achiral skyrmion bubbles can be as small as～50 nm and is comparable with room-temperature chiral skyrmions.[20，27]In previous bubble memory， the motion of achiral skyrmion bubbles can be driven by Oster fields，[23，28，29]which， however，is not superior in now spintronic devices. Recent studies have shown current-induced emergent dynamic manipulations of achiral skyrmion bubbles， such as topological skyrmionbubble transformations.[19，30]However， the current-induced coherent dynamic motions and their physical mechanisms of achiral skyrmion bubbles are less demonstrated.

Here，using a micromagnetic simulation approach，[31]we present the dynamic behaviors of achiral skyrmion bubbles driven by Zhang–Li spin-transfer-torque in uniaxial ferromagnetic stripes.[32]The role of dipole interaction in preventing the skyrmion from the central nanostripe and its potential application for neural computing is demonstrated.[33–36]Our results provide further insights into the current-induced dynamic manipulation of achiral dipole-stabilized skyrmion bubbles.

2. Methods

We used MuMax3 to simulate the current-induced dynamics of achiral skyrmion bubbles.[31]The total energy terms are given by

3. Results and discussion

Figure 1 shows the current-driven dynamic motion of a skyrmion in the ferromagnetic nanostripe withKu=54.5 kJ·m-3. The skyrmion is initialed at the center of the nanostripe. When a spin-polarized currentjalong the-xaxis with a density of 2×1011A·m-2is on， the skyrmion moves along thexaxis with an initial velocityvx=18.2 m·s-1(Fig. 1(b)). However， the velocityvxdecreases gradually to zero， the motion distanceGxreaches a maximum value of 388 nm at timet=37 ns.A reverse skyrmion motion along the-xaxis is obtained in the time dual of 37.5 ns–75.5 ns.Finally，the skyrmion stops at the distanceGx=340 nm even the currentjis still on. Once the currentjis off，the skyrmion moves along the-xaxis with an initial velocityvx=-18.2 m·s-1，whose magnitude is equal to that att=0 ns. The relaxed velocityvxdecreases when the guiding center of the skyrmionGxdecreases. Finally， the skyrmion stops at the initial center of the nanostripe，i.e.，Gx=0 nm. The results suggest that the skyrmion prefers to stay at the center of the nanostripe.To deduce the main interaction which prevents the skyrmion from moving away from the center，we also obtain the motion dependence of free energy， as shown in Fig. 1(c). The total free energy of skyrmion is not isotropic but increases asGxincreases. The exchange interactionεex，ZeemanεZeeman，and uniaxial anisotropy energiesεuall decrease asGxincreases.In contrast，only the demagnetization energyεdemincreases asGxincreases. Thus， the dipole–dipole interaction forces the skyrmion to stay at the central location of the nanostripe.

Fig.1. (a)Snapshots for current-driven motions of a skyrmion in the middle layer(z=50 nm)of a ferromagnetic nanostripe. The central location of the nanostripe is set as the original zero-point. A spin-polarized current j with a density of 1011 A·m-2 is applied for 0 ＜t ＜200 ns and then is off for t ＞200 ns. The colors white and black represent out-of-plane up and down magnetization orientations， respectively， according to the colorwheel.(b)The skyrmion motion velocity along with the x axis vx and the skyrmion guiding center Gx as a function of time t. (c)The varied total free energy density Δεtotal， exchange energy density Δεex， Zeeman energy density ΔεZeeman， uniaxial anisotropy energy density Δεu， and demagnetization energy density Δεdem as a function of time t during the motion. The gray(0 ns ＜t ＜200 ns)and white(t ＞200 ns)regions in panels(b)and(c)imply that the current is on and off，respectively. Magnetic field Bext=450 mT is applied along the z axis.

Fig.2.(a)Three-dimensional spin textures of the skyrmion in the nanostripe.(b)Enlarged cross-sectional spin textures in the red zone of panel(a).Spin configurations at the top surface z=100 nm(c)，middle layer z=50 nm(d)，and bottom surface z=0 nm(e). (f)Skyrmion location Gx dependence of increased demagnetization energy Δεdem. Magnetic field Bext=450 mT is applied along the z axis.

Fig. 3. (a) Skyrmion locations x as a function of time t for current density varying from 1×1010 A·m-2 to 40×1010 A·m-2. Inset of (a) shows the motion trajectory of the skyrmion bubble driven by the current with a density of 40×1010 A·m-2. (b) Initial transient velocity at t =0 ns vx and dynamical equilibrium distance Gx-m as a function of current density. The red curve shows the fitting velocity based on Eq. (2). Magnetic field Bext=450 mT is applied along the z axis.

Figure 3 shows the current density dependence of dynamic motion of the skyrmion bubble in the nanostripe.Skyrmions are particle-like topological magnetic objects，whose motion is described using Thiele’s collective coordinate approach.[4，17，38，39]Without the consideration of the demagnetization field，the velocity of the skyrmion bubble in our simulated case can be expressed by[4]

where the parametersg，μB，andeare the Land´e factor，Bohr magneton，and electron charge，respectively. For the skyrmion is located at the center，the skyrmion is free in motion. Thus，the initial velocityvxatGx=0 nm can be well fitted using Eq.(1)，as shown in Fig.3(b).When the skyrmion moves away from the center of the nanostripe，the repulsive force from the sample edge induced by the demagnetization field prevents the motion of the skyrmion driven by the current. Thus，the velocity decreases gradually to zero when the driving force is balanced with the demagnetization field. The balanced motion distanceGx-mincreases nonlinearly with the current density(Fig.3(b))as the increased demagnetization energy is not linear with the distanceGx(Fig.2(f)). The repulsive force from the border of geometry has been also demonstrated in chiral skyrmion motion in non-centrosymmetric magnets.[40，41]But the repulsive force plays a role only when the chiral skyrmion gets very close to the edge. In contrast， for the dipolarstabilized skyrmion bubbles in our case， the repulsive force works even if the skyrmion is 1000 nm away from the border.Noted that the skyrmion shrinks when getting approaching the edge of the nanostripe because of the repulsive force from the edge，[17]as shown inset of Fig.3(a).

The current-induced dynamic motion of the skyrmion bubble in the ferromagnetic nanostripe withη= 0.22 could be applied for artificial spiking neurons.[33–36]Artificial neural networks are promising in dealing with massive parallel tasks including pattern recognition and big data mining.[42]Artificial neural networks typically comprise synapses for memory and neurons for computing (Fig. 4(a)). Synapses have been experimentally demonstrated by current-controlled skyrmion counts.[36]The implementation of artificial neurons is mostly realized by integrating many transistors on Si-based circuits with a high energy cost and low device density.[43]The high mobility and small size of skyrmions enable promising highefficient skyrmion-based neuron devices.[33，34]The leakagelike functions of skyrmion-based neurons are proposed by the artificial design of energy gradients， which are usually obtained by very complex geometrical designs including wedgeshaped nanotracks and gradient anisotropic films.[33，34]We will demonstrate the realization of the leakage-integrate-fire(LIF) behavior of neurons (Figs. 4(d)–4(d)) using a dipolar skyrmion in the simple regular nanostripe.[44]Figure 4(e)shows the schematic neuron based on the achiral skyrmion bubble. We used pulsed spin-polarized currents as the input of spiking neuronIspk-in. The membrane potentialVmemis represented by the driving distanceGxof the skyrmion. Once the skyrmion enters the 100-nm width detection region whose center is 500 nm away from the center of the nanostripe， the spiking neuron fires an outputVoutthat is represented by the measured topological Hall voltageVTHE.[45–49]

Fig. 4. (a) Schematic biological neural network includes neurons for memory and synapses for computing. (b)–(d) LIF behavior of artificial spiking neurons. (e)Schematic neuron based on current-induced skyrmion bubble motion in a nanostripe. The red box indicates the detection zone based on the topological Hall effect. (f)Period(blue curve)and stochastic(green curve)current stimuli are used as the input of spiking neurons Ispk-in. (g)Motions of the skyrmion are driven by the period(blue curve)and stochastic(green curve)current stimuli. Once the location Gx reaches 500 nm，the device is reset with j=0 A·m-2 and fires an output topological Hall voltage VTHE. (h)The measured topological Hall voltage VTHE in the detection region during the whole LIF behavior. Magnetic field Bext=450 mT is applied along the z axis.

We considered period and stochastic waveforms of the input current stimuli(Fig.4(f))，the distanceGxof the skyrmion integrates when the current is on and leakages when the current is off (Fig. 4(g)). OnceGxreaches 500 nm， the device fires an output topological Hall voltage(Fig.4(h))that is proportional to the total charge in the detection region:[45–49]

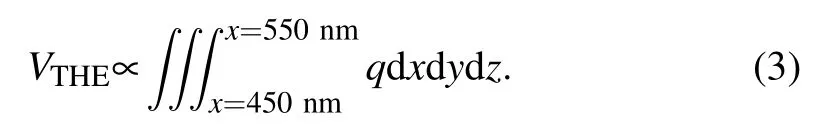
The device is then reset with zero current， the skyrmion will finally move back to the initial central locationGx= 0 nm because of the repulsive force of edge induced by the demagnetization field. Thus， the LIF behavior of artificial spiking neurons can well be mimicked by the dynamic motion of dipolar skyrmion driven by current stimuli. The LIF-like behavior is mainly contributed by the anisotropic demagnetization energy (Fig. 2(f)) in the confined nanostripe. When the periodical boundary condition along thexaxis is applied in our simulation， the demagnetization energy is then independent of the skyrmion bubble location. Thus， the skyrmion bubble can be steady driven by the current without the LIF-like behavior， as shown in Fig. 5(a). Furthermore， because the anisotropic demagnetization energy as a function of skyrmion location remains when considering the skyrmion Hall effects and thicker thickness，the LIF-like behavior inη ＜1 cases can be also achieved forα／=β(Fig.5(b))and in thicker nanostripe(Fig.5(c)).

Fig.5. (a)Current-driven dynamics of the skyrmion bubble in the nanostripe with the periodical boundary condition along the x axis. β =α，thickness=100 nm，and Bext=450 mT.(b)Current-driven dynamics of the skyrmion bubble in the nanostripe for β =2α and β =0.5α. Thickness=100 nm，Bext =450 mT without the periodical boundary condition. (c) Current-driven dynamics of the skyrmion bubble in the nanostripe with a thickness of 200 nm. β =α，Bext=450 mT without the periodical boundary condition. The gray and white regions imply that the current is on and off，respectively.

Fig. 6. 3D spin configurations for the skyrmion located at the center of the nanostripe for magnets with η =0.45 at B=400 mT (a)， η =1.12 at B=310 mT(b)，and η =4.48 at 175 mT(c). The spin configurations at the top surface z=100 nm for magnets with η =0.45(d)，η =1.12(e)，and η=4.48(f). (g)Quality factor dependence of initial averaged velocity in first 10 ns after releasing a skyrmion at Gx=500 nm. (h)Velocity and guiding center of a skyrmion driven by current in a magnet with η =4.48 at B=175 mT.The gray(0 ns ＜t ＜2 ns)and white(t ＞2 ns)regions in(h)imply that the current is on and off，respectively.

We have shown that the demagnetization field forces the skyrmion to stay at the central nanostripe， which could be used for neuron devices but is not applicable for racetrack memory.[11]We then discuss the current-induced coherent motion of the skyrmion in a stronger perpendicularly magnetized nanostripe. The quality factor is then modified by varying only the magnetic anisotropyKu. By increasing the quality factor of the uniaxial ferromagnet， we observed that the background magnetizations turn to be uniform (Figs. 6(a)–6(f)). A skyrmion is initialed atGx=500 nm， we then obtain the average relaxed velocityvrelaxin the first 10 ns after releasing the skyrmion. The relaxed velocity is proportional to the gradient of demagnetization energy along thexaxis，i.e.，vrelax∝∂εdem/∂x.[50]When the background magnetization turns to be uniform for highη(Fig. 6(c))， the gradient of demagnetization energy decreases， thus the relaxed velocityvrelaxdecreases as the quality factor increases and turns to zero forη ＞3.8 (Fig. 6(g))， suggesting the repulsive force from the edge of geometry induced by the demagnetization field is strongly suppressed for increasedη. We then test the current-induced coherent motion of a skyrmion forη=4.48(Fig. 6(h)). The skyrmion can be continuously driven by the current. Importantly，the skyrmion remains but does not move to the initial central location of the nanostripe when the current is off，providing the possible racetrack memory application.

4. Conclusions

In summary，we have shown the role of dipole–dipole interaction on motion dynamics of skyrmion bubbles in achiral uniaxial ferromagnets. The LIF and coherent motion behaviors are demonstrated for uniaxial magnets with low and high quality factors， respectively. Besides， as the dipole–dipole interaction is also important in stabilizing antiskyrmion bubbles in MnPdPtSn and hybrid skyrmion bubbles in multi-layer films with perpendicular anisotropies，[51，52]our results should also provide a guide in their current-controlled dynamic manipulations.

Acknowledgements

This work was supported by the National Natural Science Foundation of China(Grant Nos.12174396 and 12104123).