Influence of Rashba spin–orbit coupling on Josephson effect in triplet superconductor/two-dimensional semiconductor/triplet superconductor junctions
Bin-Hao Du(杜彬豪), Man-Ni Chen(陈嫚妮), and Liang-Bin Hu(胡梁宾)
Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials,School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou 510631,China
Keywords: Josephson effect,Rashba spin–orbit coupling,triplet superconductor,0-π transitions
1. Introduction
In recent years, the study of various effects related to spin–orbit interaction (SOI) of conducting electrons in solidstate materials and their hybrid structures has been an active research field in condensed matter physics. Such studies are not only of fundamental interest but also of practical importance because they may provide some potential routes for spinbased electronics(spintronics)and quantum computation.[1,2]And in this context, strong SOI intrinsic in some narrow-gap semiconductors or topological insulators and various effects related to them have attracted considerable interest.The strong SOI intrinsic in such materials may originate from bulk inversion asymmetry[3]or structural inversion asymmetry due to confining potentials[4]and can be externally controlled by the application of electric field, gate voltage, or mechanical strain,etc., for instance.[5–7]Such tunability has a great potential for the application to spintronic devices and quantum information processing. A variety of interesting phenomena were predicted based on such strong SOI,to name a few,spin Hall effect[8–11]and quantum spin Hall effect,[12,13]topological insulators,[14]topological superconductivity,[15]etc.
An interesting subject within these studies is that what influences strong SOI may have on Josephson supercurrent when two superconductors having a phase differenceφis connected by a semiconductor channel with strong SOI.This issue has been investigated recently for a variety of junctions containing various semiconductor nanostructures with strong SOI,such as quantum dots,[16–19]carbon nanotubes,[20,21]semiconductor nanowires,[22–25]2D electron gas,[26]and others.[27]The possibility to control various parameters of the nanostructures allows one to explore different influences of strong SOI on Josephson effect in such devices. It was predicted that Josephson supercurrents through such nanostructures may exhibit a number of novel features. For instance, in some nanostructures the coexistence of strong SOI and Zeeman effect can induce a supercurrent atφ=0,the so-called anomalous Josephson current.[25–32]From a generic point of view,such novel features arise from the specific spin structure on the Fermi surfaces due to the spin–orbit coupling,which plays an important role in connection with Josephson effect.
In this work we investigate theoretically Josephson effect in planar ballistic junctions consisting of two triplet superconductors (TSCs) withp-wave orbital symmetries and connected by a 2D semiconductor channel with strong Rashba SOI. While there has been a growing interest in understanding coherent transport phenomena in Josephson junctions with strong SOI, most of previous studies were focused on hybrid heterostructures involving conventional superconductors with spin-singlet pairing ands-wave orbital symmetry. From theoretical points of view, since the pairing potentials are momentum-dependent and change sign on the Fermi surface and the Cooper pairs take the forms of spin-triplet pairing in TSCs, different behaviors would be anticipated compared to the singlet cases.[33,34]For example, due to the intimate relationship between spin-triplet pairing and ferromagnetism,one would anticipate that the effect of strong Rashba SOI, which behaves as a momentum-dependent effective magnetic field,may have sensitive dependence on the orientation of Rashba effective field relative to the TSC vector order parameter, a key parameter of such systems.[35]Moreover,in such systems zero-energy bound states may form at interfaces in a junction,which may also affect significantly the transport properties of a junction.[36]In view of these facts, a deeper understanding of the effect of strong SOI and its interplay with Zeeman magnetic field upon Josephson supercurrents in such systems is desirable. In the current study, we focus on the coherent transport in connection with Josephson supercurrents in planar ballistic junctions consisting of two triplet superconductor leads withp-wave orbital symmetries and connected by a 2D semiconductor channel with strong Rashba SOI.Using the Bogoliubov–de Gennes(BdG)formalism,we investigate systematically the effect of strong Rashba SOI and its interplay with Zeeman effect upon coherent transport in connection with Josephson supercurrents in such junctions.
The paper is organized as follows. In Section 2 we illustrate the theoretical model and the solution of the scattering problem used for the calculations of Josephson supercurrents.In Section 3 we present the numerical results for Josephson supercurrents and current-phase relations obtained by use of the formalism illustrated in Section 2. The features of the variations of supercurrents and current-phase relations with the changes of relevant physical parameters are investigated in some detail. A summary is given in Section 4.
2. Model and formulation
The system under current study is a planar ballistic junction consisting of two identicalp-wave superconductors connected by a 2D semiconductor channel with strong Rashba SOI.The junction is grown along thezdirection and lies in they–zplane. The two interfaces between the two superconductor leads and the semiconductor channel are located atz=0 andz=L, respectively, and extend along theydirection. An out-of-plane Zeeman magnetic field is applied along thexdirection in the semiconductor channel. The BdG equation for quasiparticle(QP)states in the system is given by


wherek=(ky,kz)is the 2D wave vector,σ0is the 2×2 identity matrix,andσ=(σx,σy,σz)the Pauli matrices,Θ(z)is the step function,αRis the strength of Rashba SOI in the semiconductor channel,Vx=gμBBis the Zeeman energy, withBthe magnitude of the Zeeman field andgthe Lande factor andμBthe Bohr magneton. For simplicity, we assume equal effective massmand chemical potentialμin all regions of the junction.

wheredL,Rdenote thedvectors in the left (L) and right (R)superconductor leads andΔL,R(k) the superconducting order parameters, respectively. In particular, we assume that thedvectorsdL,Rlie in thex–yplane and their orientations are defined two anglesaLandaR, respectively, whereaL,Ris the angle between thexaxis anddL,R. The explicit forms ofdL,Rare then given by

The Josephson supercurrent is related to a difference in the overall phases of the superconducting order parameters in the left and right leads of the junction. We assume that the two superconductor leads differ only in a overall phase of the order parameter,with

in whichΔ(k)denotes the orbital pairing states andφthe overall phase difference of the superconducting order parameters.We will consider three types of orbital-pairing states,with

We first solve the BdG equations separately in different regions of the junction to obtain the eigenfunctions of quasiparticles(QPs). For dc Josephson effect,only low-energy excitations (withμ ≫E,|Δ(k)|) are involved. Under this assumption,the wave vectors can be regarded as approximately equal in magnitude for electron-like and hole-like QPs in the superconducting regions,i.e.,ke≈kh≈kF,the so-called Andreev approximation. For convenience, in the following we will use a superscript L (R) in the eigenfunctions to denotes QPs in the left lead(z <0)or in the right lead(z >L)of the junction and use a subscripts r (l) to denote right-going (leftgoing) QPs. Definingk ≡(kz,ky) = (kFcosθ,kFsinθ) and-^k ≡(-kz,ky),whereθis the angle of the wave vectorkof a QP relative to thezdirection, the eigenfunctions of rightgoing (left-going) QPs in the left lead (z <0) or in the right lead(z >L)of the junction can be given by

The corresponding eigenfunctions of right-moving (leftmoving) electrons (holes) in the semiconductor channel between the two superconductor leads will be denoted asψe(h),r(l),γ, in which the subscriptsγ(=+ or-) denote the spin helicity. Since the system is translational invariant along theydirection, theycomponent of the wave vector is conserved when a QP is transmitted through the interfaces between the superconductor leads and the semiconductor channel. For electrons(holes)with energyEand theycomponentkyof the wave vector,the eigenfunctions of right-moving(leftmoving) electrons (holes) in the semiconductor channel can then be expressed as


whereCe,r(l),γis the normalization factor,s= + for rightmoving ands=- for left-moving electrons (holes),kz,e(h),γdenotes thezcomponent of the wave vector of an electron(hole) with the spin helicityγ, andu↑,u↓,v↑,v↓are defined by
Note that the wave vectorske(h),γdepend on both the Rashba SOI strength and the Zeeman energy in the semiconductor channel. This has significant influence on the propagation of electrons and holes in the semiconductor channel. For example, if the Zeeman energyVx >μandαR=0, the wave vectorske(h),-of minority-spin QPs will be imaginary, implying that their propagations will be exponentially suppressed in the semiconductor channel.
Now we consider the scattering problem of QPs through the junction. By use of the eigenfunctions(9)–(12)and(18)–(19),the following wavefunction ansatz can be constructed for a spin-σelectron-like QP injected from the left lead of the junction:
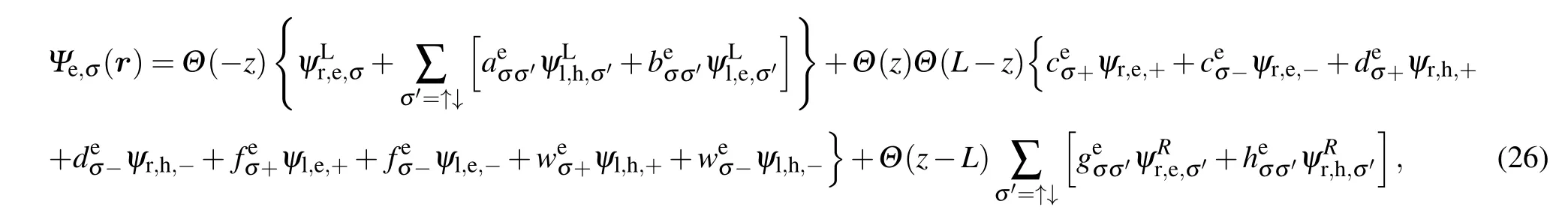

where



where the energy argument is analytically continued to Matsubara frequencies[E →iωn=i(2n+1)π/β]andβ=1/kBT.
3. Results and discussion
In this section we present the numerical results obtained by using the formalism outlined above. For convenience, in the numerical calculations we re-scale the strength of Rashba SOI to a dimensionless parameterα ≡2mαR/¯h2kF, and the superconducting pairing potentialΔ0and the Zeeman energyVxare both measured in units of the chemical potentialμ. The temperatureTis measured in units of the critical temperatureTcand the lengthLof the semiconductor channel between two superconductor leads is measured in units of 1/kF. The supercurrent is measured in units ofeΔ0/¯h.
For clarity, we first investigate the effect of Rashba SOI in the absence of Zeeman effect. We calculate numerically the supercurrent as a function of the phase differenceφof the superconducting order parameters for several different values of the Rashba SOI strengthαand the Zeeman energyVx=0.The corresponding results forpy-wave pairing,pz-wave pairing,and(pz+ipy)-wave pairing are plotted in Figs.1(a)–1(c),respectively.From Figs.1(a)–1(c)one can see that,in the presence of Rashba SOI,the current-phase relations are still nearly in the ordinary form of a sinusoidal function for the three types of orbital symmetries, as in the absence of Rashba SOI. But the magnitude of supercurrent can be changed significantly in the presence of Rashba SOI and can be tuned effectively by varying the strength of Rashba SOI.More interestingly, from Figs. 1(a)–1(c) one can see that the so-called 0–πtransitions can be driven by varying the strength of Rashba SOI,i.e., as the strength of Rashba SOI is varied, the direction of supercurrent is reversed at some critical values of the Rashba SOI strength and the current-phase relation changes from the form ofI(φ)∝sinφ(0-state)to the form ofI(φ)∝sin(φ+π)(πstate),orvice versa.Such transitions can be more clearly illustrated by analyzing the sign changes of the supercurrentI(φ)at a fixed phase differenceφwith the variation of the Rashba SOI strengthα. In Figs.2(a)–2(c)we plotI(φ)atφ=π/2 as a function of the Rashba SOI strengthαforpy-wave andpzwave and(pz+ipy)-wave pairing,respectively. Figures 2(a)–2(c)show that the magnitudes of the supercurrents atφ=π/2(the critical supercurrents)oscillate in an approximately periodic way with the variation of the Rashba SOI strengthα,but the amplitudes of the oscillation decrease gradually with the increase ofα. Accompanying with the oscillation of the magnitude of supercurrent,the direction of supercurrent is reversed for several times at some critical values of the parameterα,resulting in a sequence of 0–πtransitions. In Fig. 2(a)–2(c),the sequence of alternating 0 andπstates is separated by a sequence of critical points of the parameterαat which the supercurrent changes sign,beginning with a 0-state atα=0 for all the three types of pairing symmetries. Since the strength of Rashba SOI can be tuned by electrical means, this result suggests that it is possible to realize 0–πtransitions by electrical means. We also note that as the Rashba SOI strength is varied,the magnitude of the supercurrent remains vanishing atφ=0,i.e.,no anomalous Josephson supercurrent is exhibited,unlike the results found in somes-wave Josephson junctions with Rashba SOI.[25–32]
From Fig. 2(a)–2(c) one can note that the features of the oscillations of the supercurrents with the variation of the Rashba SOI strength depend on the orbital symmetries of the pairing potentials in the superconducting leads. For example, for the cases ofpy-wave pairing, the amplitude of the oscillation of the supercurrent with the increase of the parameterαdecreases rapidly, while for the cases ofpz-wave and (pz+ipy)-wave pairing, the amplitude of the oscillation of the supercurrent with the increase of the parameterαdecreases more slowly. For the cases ofpy-wave pairing shown in Fig. 2(a), the oscillation of the supercurrent is substantial only in the range ofα <1. Outside this range,the oscillation of the supercurrent is much weak and the oscillation almost can not result in 0–πtransition as the value ofαis increased.In the range ofα >1.5,theπ-state is much robust to increasingαand no 0–πtransitions are observed. In contrast, for the cases ofpz-wave and (pz+ipy)-wave pairing shown in Figs. 2(b) and 2(c), the oscillations of the supercurrents with the variation of the parameterαare substantial and can lead to 0–πtransitions in a more wide range of the parameterα. For a given value of the parameterα,whether the ground state is a 0-state or aπ-state also depends on the orbital symmetries of the pairing potentials in the superconducting leads. For example,for the cases shown in Fig.2(a)–2(c),the ground state is a 0-state atα=0.5 forpy-wave pairing but is aπ-state forpz-wave and(pz+ipy)-wave pairing.

Fig. 1. The supercurrent as a function of the phase difference φ of the superconducting order parameters for several different values of the Rashba SOI strength α. The corresponding results for py-wave and pz-wave and(pz+ipy)-wave pairings are plotted in panels(a),(b),and(c),respectively. The values of the parameter α are shown in the figures. The other parameters are Δ0/μ =0.001,Vx=0,T/Tc=0.4,kFL=20,aL=aR=0.

Fig. 2. The supercurrent at the phase difference φ =π/2 as a function of the Rashba SOI strength α for (a) py-wave pairing, (b) pz-wave pairing, (c)(pz+ipy)-wave pairing,respectively. The parameters are Δ0/μ =0.001,Vx=0,T/Tc=0.4,kFL=20,aL=aR=0.
From the theoretical point of view, for the system considered above,when a QP incident from one superconducting electrode is reflected at the junction interfaces or is transmitted to the other superconducting electrode through the semiconductor channel between them, since theycomponent of the wave vector is conserved but thezcomponent is not conserved,the strength of the pairing potential experienced by a QP does not change if the orbital symmetry of the pairing potential ispy-wave type but will be changed if the orbital symmetry ispz-wave or (pz+ipy)-wave type. The phase changes of the wave functions of reflected (or transmitted) QPs will also be different for different orbital symmetries. Due to such differences,the features of the oscillations of the supercurrents with the variation of the Rashba SOI strength depend on the orbital symmetries of the pairing potentials in the superconducting leads,and compared with the cases ofpy-wave pairing,the oscillations of the supercurrents with the variation of the Rashba SOI strength are more substantial in the cases ofpz-wave or(pz+ipy)-wave pairing, as shown in Fig. 2. And from this point of view,one may expect that thepz-wave or(pz+ipy)-wave type of junctions should be the optimal for observing such oscillations in experiments.
The effects of Rashba SOI illustrated in Figs. 1 and 2 are similar to that of an external magnetic field. This is reasonable since Rashba SOI is equivalent to a momentumdependent Zeeman field in principle. To illustrate this point more clearly, in Figs. 3(a)–3(c) we plot the supercurrent as a function of the phase differenceφof the superconducting order parameters for several different values of the Zeeman energyVxand the Rashba SOI strengthα= 0 forpy-wave andpz-wave and(pz+ipy)-wave pairings,respectively,and in Figs. 4(a)–4(c) we plot the corresponding results for the supercurrent at the phase differenceφ=π/2 as a function of the Zeeman energyVx. From Figs. 3 and 4 one can see that, in the regimeVx/μ <1,the supercurrent exhibits significant oscillations with the increase of the Zeeman energyVx, similar to that as shown in Figs. 1 and 2. In the regimeVx/μ >1,the supercurrent is suppressed significantly. This suppression is due to the fact that the wave vectorke(h),-of minority-spin QPs become imaginary whenVx/μ >1(as can be seen from Eq.(25))and their propagations in the semiconductor channel between the two superconductor leads is exponentially suppressed and hence do not contribute to the supercurrent. In the regimeVx/μ <1,the magnitude of the supercurrent decreases in an oscillatory manner with the increase of the Zeeman energyVx,and accompanying with the oscillation of the magnitude of the supercurrent, the direction of the supercurrent is also reversed for several times,i.e., the oscillation of the supercurrent with the increase of the Zeeman energy also leads to a sequence of 0–πtransitions. In Fig.4(a)–4(c),such transitions are indicated by the sign changes of the supercurrent at some critical values ofVx,which separate a sequence of alternating 0 andπstates,beginning with a 0-state atVx=0 for all the three types of pairing symmetry.

Fig.3. The supercurrent as a function of the phase difference φ of the superconducting order parameters for several different values of the Zeeman energy Vx.The corresponding results for py-wave pairing, pz-wave pairing,and(pz+ipy)-wave pairing are plotted in panels(a),(b),and(c),respectively. The values of Vx (in units of μ)are shown in the figures. The other parameters are Δ/μ =0.001,α =0,T/Tc=0.4,kFL=20,aL=aR=0.

Fig.4. The supercurrent at the phase difference φ =π/2 as a function of the Zeeman energy Vx for(a) py-wave pairing,(b) pz-wave pairing,(c)(pz+ipy)-wave pairing,respectively. The parameters are Δ0/μ =0.001,α =0,T/Tc=0.4,kFL=20,aL=aR=0.
If both Rashba SOI and Zeeman magnetic field are present, the supercurrent and current-phase relation will depend both on Rashba SOI and Zeeman magnetic field. In such cases, some features of the supercurrents and current-phase relations illustrated above may be altered significantly if the interplay of Rashba SOI and Zeeman magnetic field is strong.As an example, in Figs.5(a)–5(c)we plot the supercurrent at the phase differenceφ=π/2 as a function of the Zeeman energyVxfor several different values of the Rashba SOI strengthα. From Figs. 5(a)–5(c) one can see that, in the presence of the interplay of Rashba SOI and Zeeman effect,the 0–πtransitions can still be driven by varying the strength of Zeeman magnetic field or varying the strength of Rashba SOI,but the basic patterns of the variations of the supercurrents with the relevant parameters may be altered significantly due to their interplay. For instance, for the cases withα=0.1 in Fig. 5,the variations of the supercurrent with the Zeeman energyVxare similar to that as shown in Fig. 4. But as the value ofαis increased,e.g., for the cases withα=1, the onset of the oscillation of the supercurrent will require a largerVxand the oscillation will become smoother and smoother. As the value ofαis increased further, the oscillation of the supercurrent may eventually be smeared out(e.g.,for the cases withα=2 in Fig.5).Another interesting result of the interplay of Rashba SOI and Zeeman effect is that,if the value ofαis sufficiently large,the supercurrent will not be suppressed completely even whenVx/μ >1. Such features are different from that illustrated in Fig. 4. From the theoretical point of view, Rashba SOI not only modify the spin structure on the Fermi surfaces and change the Fermi momenta which affect the Josephson supercurrent but also cause precession of the spins of QPs,which tends to wash out the spin polarization of QPs due to Zeeman effect. In strong spin–orbit coupling regime, the Andreev reflection may be influenced significantly by the wash-out of the spin polarization of QPs and hence the suppression of Josephson supercurrent due to Zeeman effect may be weakened even whenVx/μ >1. This is similar to the result obtained in a recent study,[35]where the interplay of Rashba spin–orbit coupling and Zeeman effect on the tunneling conductance of a 2D Rashba metal/superconductor junction is investigated. It was found that, when the Zeeman energy is larger than the Fermi energy,the zero-bias conductance is suppressed in weak spin–orbit coupling regime but may revive in strong spin–orbit coupling regime.[35]
In all cases considered above we have assumed that the directions of thedvectors in two superconducting leads of a junction are parallel to each other and bothdLanddRare along thexaxis,with the anglesaL=aR=0. From the theoretical point of view,the relative orientations of thedvectors in different superconducting leads of a junction may also have significant influence on coherent transport of QPs in connection with Josephson supercurrent. To illustrate this point, we keep the direction ofdLalong thexaxis and rotatedRin thex–yplane,i.e., keeping the angleaL=0 and varying the values of the angleaR. In Fig. 6 we plot the supercurrent as a function of the phase differenceφof the superconducting order parameters foraR=0,π/2,andπ,respectively. The other parameters areΔ/μs=0.001,α=0.1,Vx=0.1,T/Tc=0.4,kFL=20. For the parameters chosen, the ground state of the junction is a 0-state foraR=0 (the directions ofdLanddRare parallel to each other) and is aπ-state foraR=π( the directions ofdLanddRare antiparallel to each other)for all the three types of orbital symmetries considered. ForaR=0 andaR=π, the periodicity of the current-phase relationship is 2π. ForaR=π/2,the periodicity of the current-phase relationship isπbut not 2π,indicating that the sinφcomponent of the Josephson supercurrent is suppressed and the sin2φcomponent is enhanced when the directions of thedvectors in two superconducting leads are perpendicular to each other. Such differences indicate clearly that inp-wave Josephson junctions the relative orientations of thedvectors in different superconducting leads may have significant influence on Josephson supercurrent, and both the magnitude of supercurrent and the current-phase relation may be manipulated effectively by tuning the relative orientations of thedvectors in different superconducting leads. Such features are significantly different from that found in conventionals-wave Josephson junctions.

Fig.5. The supercurrent at the phase difference φ =π/2 as a function of the Zeeman energy Vx for several different values of the Rashba SOI strength α.The corresponding results for py-wave pairing, pz-wave pairing,and(pz+ipy)-wave pairing are plotted in panels(a),(b),and(c),respectively. The values of the Rashba SOI strength α are shown in the figures. The other parameters are Δ/μs=0.001,T/Tc=0.4,kFL=20,aL=aR=0.

Fig. 6. The supercurrent as a function of the phase difference φ of the superconducting order parameters for several different values of the angle aR. The corresponding results for py-wave pairing, pz-wave pairing,and(pz+ipy)-wave pairing are plotted in panels(a),(b),and(c),respectively. The values of the angle aR are shown in the figures. The other parameters are Δ/μs=0.001,α =0.1,Vx=0.1,T/Tc=0.4,kFL=20,aL=0.
4. Conclusion
In summary, we have theoretically studied the influence of Rashba SOI on Josephson effect in junctions consisting of two spin-tripletp-wave superconductors connected by a 2D semiconductor channel with strong Rashba SOI. The variations of the supercurrent and current-phase relation with the relevant physical parameters are investigated in some detail. It is found that the magnitude of the supercurrent exhibits signifciant oscillations with the Rashba SOI strength,but the amplitude of the oscillation decreases gradually with the increase of the Rashba SOI strength. Accompanying with the oscillations of the magnitude of the supercurrent, 0–πtransitions may also be driven by varying the Rashba SOI strength. It is also shown that if both Rashba SOI and Zeeman magnetic feild are present,the signifciant oscillation of the supercurrent with the Rashba SOI strength or with the magnetic feild strength may be suppressed substantially or may even be smeared out by their interplay. Furthermore, it is shown that the relative orientations of thedvectors in two superconducting leads of a junction may also play an important role in the supercurrent and the current-phase relationship, and 0–πtransitions can also be realized by changing the relative orientations of thedvectors in two superconducting leads.
- Chinese Physics B的其它文章
- Real non-Hermitian energy spectra without any symmetry
- Propagation and modulational instability of Rossby waves in stratified fluids
- Effect of observation time on source identification of diffusion in complex networks
- Topological phase transition in cavity optomechanical system with periodical modulation
- Practical security analysis of continuous-variable quantum key distribution with an unbalanced heterodyne detector
- Photon blockade in a cavity–atom optomechanical system

