Tunable anharmonicity versus high-performance thermoelectrics and permeation in multilayer(GaN)1-x(ZnO)x

Hanpu Liang(梁汉普) and Yifeng Duan(段益峰)

School of Materials and Physics，China University of Mining and Technology，Xuzhou 221116，China

Keywords: thermal transport，anharmonicity，thermoelectricity，nonisovalent alloys

1. Introduction

Nonisovalent(GaN)1-x(ZnO)xalloys introduce a variety of potential applications in optoelectronic and thermoelectric devices，due to the abrupt reduction of band gap，compared to their binary counterparts.[1–9]Moreover， dimensional reduction always introduces significant changes in structural configurations and physical properties.[10，11]The few-layer haeckelite phase is more energetically stable and suitable in optoelectronic applications than the wurtzite structures， because that the nearly zero internal electrostatic field (IEF) greatly enhances optical absorption efficiency.[12]The lack of 2D configurations as well as complete stoichiometries hinders to further explore physical properties，e.g.， optical absorption and thermal transport. For example， an open question is how the electronic band gap evolves with ZnO composition. In theory，due to the same crystal symmetry and the very close lattice constants， GaN and ZnO can combine in many ways to form various 2D compounds and structures，especially in multilayer configurations. We aim to establish stable multilayer phases as well as complete stoichiometries in 2D (GaN)1-x(ZnO)x，which remain unclear so far and are expected to provide novel performances better than their binary counterparts.

It is a hot issue on how to strengthen the anharmonicity，since the thermoelectric performance is effectively improved by the ultralow lattice thermal transport. The asymmetrical charge distribution is much close to the structural properties，e.g.， in the lone pair cation systems.[13–20]The irregular configurations are adopted to destroy the symmetry in charge distribution，e.g.， the square，[21]pentagon，[22]octagon，[23]and other irregular structures.[24，25]In multi-layer structures， the interlayer interactions inspire more phonon vibrational modes，therefore，it is feasible to further suppress the thermal transport and thus to continue to improve the thermoelectrics. However， the novel effects were seldom reported so far because of the lack of multilayer configurations. In van der Waals(vdW) SnSe，[26]a moderate interlayer distance induces high thermoelectric performance by overlapping the antibonding state wave functions in the out-of-plane direction. Herein，due to the very close electronegativity and atomic size in 2D(GaN)1-x(ZnO)x， it is much promising for multilayer configurations to be stable at ambient conditions. The interlayer interactions via covalent bonds introduce more asymmetry into the charge distributions， thus the stronger anharmonicity further improves the thermoelectrics. Therefore，it is technologically necessary and important to deeply explore multilayer(GaN)1-x(ZnO)x， which would provides more colorful properties in the fields of physics，chemistry and materials.

Adsorption- and permeation-based selection processes are key to evaluate the ionic transport properties in porous multilayer alloys.[27，28]For example， monolayer T-C3N，which is inspired by T-carbon，[29]is a good semipermeable membrane for desalination and can permeate the H2O molecular at room temperature，because of the large porous.[30]Multilayer MoS2shows the high H2/CO2separation performance at the excellent H2permeability at the high-temperature 2H phase， which decreases the interlayer space and enlarges the interbundle spaces and thus increases the gas permeability.[31]Therefore，to deeply explore the application potential in multilayer (GaN)1-x(ZnO)xmaterials， a comprehensive understanding of the ionic adsorption/permeation processes is necessary.

In the present study， we identify the stable multilayer (GaN)1-x(ZnO)xas wurtzite-likePm-(GaN)3(ZnO)1，Pmc21-(GaN)1(ZnO)1，andP3m1-(GaN)1(ZnO)2，and haeckeliteC2/m-(GaN)1(ZnO)3using an evolutionary variablecomposition searches based on first-principles calculations.The interlayer coupling indeed greatly enhances the thermoelectrics due to the intrinsically ultralow lattice thermal conductivity because of the stronger anharmonicity by the asymmetry in charge distributions. The anomalous band structure versus ZnO composition is attributed to the forbiddenp–dcoupling inC2/m-(GaN)1(ZnO)3from the group theory， which is helpful to modulate the optoelectronic performance. Finally，we uncover the remarkable Na+/H+selectivity in Na+aqueous solution by the multilayer configurations.Our work would stimulate deeper understanding of the nonisovalent semiconductors.

2. Computational methods

Stable phases in the 2D system are predicted using a first-principles variable-composition evolutionary algorithm as implemented in the USPEX code.[32–34]At each promising composition， the fixed-composition searches are carried out，in combination with structural relaxations and total energy calculations using the density functional theory (DFT[35，36])within the generalized gradient approximation parameterized by the PBE.[37]The projector augmented wave method[38，39]implemented in the VASP package[40–42]is employed. The vdW interaction is considered by the vdW-DF2 exchange functional.[43]The band alignments are aligned with respect to the vacuum level. We adopt the plane-wave energy cutoff of 500 eV， andΓ-centeredk-point meshes for sampling the Brillouin zone with a reciprocal-space resolution of 2π×0.05 ˚A-1. The electronic band structures are calculated by the HSE06 hybrid functional.[44]Electronic transports are calculated by the semiclassical Boltzmann transport equation within the constant relaxation time approximation in the BoltzTraP package.[45]Phonon dispersion and the second-order interatomic force constants (IFCs) are calculated by the Phonopy package.[46]The third-order IFCs and the lattice thermal conductivity are evaluated by the ShengBTE.[47]During structural searches，the initial population includes 80 structures with up to 16 atoms per primitive cell， with the thickness of 2D crystals in a range from 0 ˚A to 6 ˚A. The succeeding generations are obtained from heredity(50%)，softmutation(10%)，transmutation operators(10%)，and randomly symmetric generator(30%).

To describe the thermal transport，the IFCs are calculated by applying a small displacement on one atom.The high-order term of interatomic potential dominates the anharmonic effect from the collision between phonons. Three-phonon scattering processes，including absorption(+)and emission(-)，satisfy the energy and momentum conservations

TheKis zero for normal process and nonzero for umklapp process. In the phonon Boltzmann transport equation(BTE)，the lattice thermal conductivity is defined as[47]

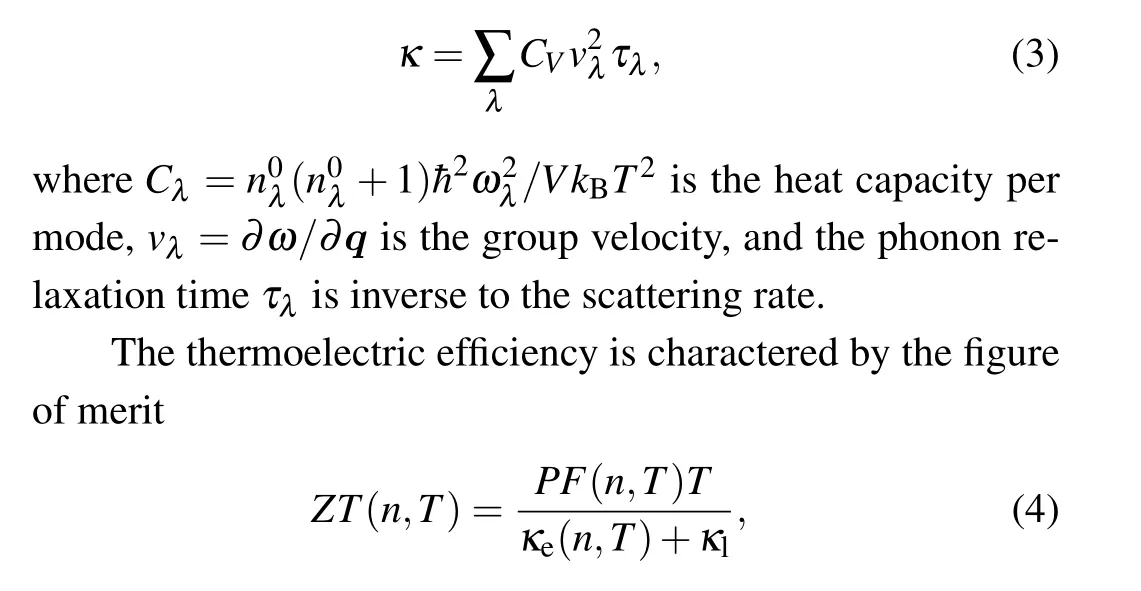
wherenandTare the carrier concentration and temperature，respectively. The power factorPF(n，T) describes the electronic features inZT，andκeandκlare the electronic and lattice thermal conductivities，respectively.

3. Results and discussion

The 2D GaN and ZnO share the most stable planar hexagonalsp2configuration and was successfully fabricated by reconstructing the bulk wurtzite into the graphite structure[48，49](see Figs.1(a)and 1(b)). The band gaps atΓpoint of hexagonal GaN(h-GaN)and ZnO(h-ZnO)are 3.71 eV and 3.30 eV，respectively. Although the valence band maximum(VBM)is atMpoint in h-GaN，the main optical absorption occurs atΓdue to the much higher conduction band minimum(CBM)atMthan atΓpoint (see Fig. 1(c)). The stable phases of 2D(GaN)1-x(ZnO)xare identified by the complete convex hull，which is expressed by the formation energy (see Fig. 1(d))，with h-GaN and h-ZnO as the starting-and ending-points，respectively. A structure on the convex hull is thermodynamically stable， while above the hull is metastable. The groundstate multilayer configurations appear at the 1/4，1/2，2/3，and 3/4 stoichiometries with thePm，Pmc21，P3m1， andC2/msymmetries， respectively (see Figs. 1(e)–1(h)). Phonon spectra and stress-strain relationship are shown in Figs.S1 and S2 in the Supplemental materials(hereafter SM)，as well as structural parameters and elastic constants listed in Tables S1 and S2，which indicate that the predicted configurations satisfy the dynamical and mechanical stability.[50]

Fig.1. (a)Structural model of the hexagonal lattice. (b)Distributions of GaN and ZnO in the periodic table. (c)Electronic band structures of hexagonal GaN and ZnO monolayers. (d)Thermodynamic convex hull of 2D GaN–ZnO multilayers at ambient conditions. The stable and metastable phases are highlighted in red and gray dots， respectively. Crystal structures， schematic diagrams of structural force， and ELF of top and side views in (e) Pm-(GaN)3(ZnO)1，(f) Pmc21-(GaN)1(ZnO)1， (g) P3m1-(GaN)1(ZnO)2， and (h) C2/m-(GaN)1(ZnO)3. Red， gray， blue， and green balls represent Ga， N， Zn， and O atoms，respectively.

To suppress the IEF is the key to stabilize the multilayer configurations，since the strong dipoles associated with the opposite charges on surfaces tend to destabilize the structure. InPm-(GaN)3(ZnO)1， the difference in atomic species induces the deformed tetrahedrons，e.g.， the bond angles around Zn and O atoms derivating from～109°to～118°and～113°，respectively. The close electronegativity and atomic size prefer the planar layers to reduce the in-plane IEF and thus stabilize the configuration. InPmc21-(GaN)1(ZnO)1， the interlayer Ga–N bonds are overall alternately arranged in opposite directions to reduce the dipole moments along the[001]direction.P3m1-(GaN)1(ZnO)2displays the planar configuration and the alternate arrangements of interlayer dipoles in opposite directions，thus the net IEF is nearly zero both in the plane and along the out-of-plane direction. Furthermore， the interlayer Bader charge and bond length are～0.04eand～2.28 ˚A，while the in-plane results are～1.32eand～1.90 ˚A， which agree well with 1.34eand 1.86 ˚A in monolayer GaN.[51]This implies that the in-plane interactions dominate the structural configuration rather than the interlayer interactions. HaeckeliteC2/m-(GaN)1(ZnO)3is constructed by the alternating octagons and squares along the [110] direction and exhibits a nearly zero IEF along the [001] direction since the adjacent dipoles have opposite directions.

Figure 2(a)illustrates the optical absorption coefficients，where the absorption thresholds perfectly match the band gaps at theΓpoint. Although， inP3m1-(GaN)1(ZnO)2， the VBM is at theKpoint， similar to hexagonal GaN and ZnO monolayers，[48]the main absorption actually occurs at theΓ，due to the 4.37 eV higher CBM at theKthan at theΓ. It is remarkable that the absorption intensity inC2/m-(GaN)1(ZnO)3is stronger at least two times than that in other structures due to the nearly zero IEF according to the quantum confined Stark effects.[12]Thereby， this structure is more promising in lighting devices with excellent absorption efficiency. Although the nearly zero IEF is also realized inP3m1-(GaN)1(ZnO)2， the covalent bonds by fivefold-coordinated atoms do not originate from the conventionalsp2orsp3hybridization，as a result，the higher-symmetry bonding significantly suppresses the optical absorption.

The band gap increases from 1.87 eV inPm-(GaN)3(ZnO)1to 2.51 eV inPmc21-(GaN)1(ZnO)1， and to 3.00 eV inP3m1-(GaN)1(ZnO)2， but unexpectedly slightly decreases to 2.91 eV inC2/m-(GaN)1(ZnO)3. This is consistent with that the symmetry first rises fromCstoC2vand toC3v， and then drops toC2h， thereby the anomalous trend closely correlates with the group theory and thep–dcoupling.When thepanddorbitals have the same irreducible representations，thep–dcoupling occurs(see Fig.2(b)). In multilayer(GaN)1-x(ZnO)x， the N-2porbital dominates the VBM and the binding energy is much smaller in Zn-3dorbital than in Ga-3d(see Fig.S3)，thus the possiblep–dcoupling originates from N and Zn atoms(see Fig.2(c)).

Table 1 reveals that thepanddorbitals have one common representation (A′) inPm-(GaN)3(ZnO)1， three (A1，B1，andB2)inPmc21-(GaN)1(ZnO)1and all(A1andE)inP3m1-(GaN)1(ZnO)2，thus thep–dcoupling is allowed，i.e.，Vp–d ／=0. The coupling strength is defined as

which is inversely proportional to the energy differenceεp–εdbetween thepanddorbitals. According to thep–dcoupling theory，[52–54]as the symmetry continuously rises， the down-shift ofdorbital greatly weakens thep–dcoupling and thereby enhances the band gap (see Fig. 2(d)). InC2/m-(GaN)1(ZnO)3， N-3porbital belongs to theAuandBurepresentations， while Zn-3dorbital belongs to theAgandBgrepresentations. Thepanddorbitals have distinct representations， thereby thep–dcoupling is forbidden，i.e.，Vp–d=0.Meanwhile， inP3m1-(GaN)1(ZnO)2， the huge differenceεp–εdmakes the coupling negligible in the band structure，thus the band gaps are very close to each other inP3m1-(GaN)1(ZnO)2andC2/m-(GaN)1(ZnO)3. Moreover， due to the lack ofp–dcoupling，the band alignment ofC2/m-(GaN)1(ZnO)3is overall higher than the others.

Table 1. Irreducible representations of p and d orbitals in the Cs，C2v，C3v，and C2h point groups，respectively. In the Cs，C2v，and C3v symmetries，the p–d coupling is allowed and is forbidden in the C2h symmetry.

Fig.2. (a)Optical absorption coefficients and band gaps(inserted panel)in multilayer GaN-ZnO.(b)Shapes of p and d orbitals. (c)Sketches p–d atomic orbital hybridization. (d) Band alignments of the VBM and CBM with respect to the vacuum level. (e) Electronic band structures in Pm-(GaN)3(ZnO)1，Pmc21-(GaN)1(ZnO)1，P3m1-(GaN)1(ZnO)2，and C2/m-(GaN)1(ZnO)3. The inserted panels are the partial charge distribution at the VBM.

Figure 3(a) displays the lattice thermal conductivityκLby solving the phonon BTE with the iterative method， which is determined by the phonon relaxation timeτλ， the phonon group velocityvλ， and the volumetric specific heat capacityCv. At room temperature， the lowestκLis～3.1 W/mK inP3m1-(GaN)1(ZnO)2， the highestκLis～42.3 W/mK along the armchair direction inPmc21-(GaN)1(ZnO)1，which，however， is much smaller than in most 2D materials. TheκLis～27.2 W/mK and 12.1 W/mK inPm-(GaN)3(ZnO)1andC2/m-(GaN)1(ZnO)3，respectively. The dependence ofκLon the phonon mean-free-path (MFP) is plotted in the inserted panel for multilayer (GaN)1-x(ZnO)xreveals that， to maximize theκL，the boundary sizes are required to be larger than 104nm.

Fig. 3. (a) The temperature-dependent lattice thermal conductivity as well as the thermal conductivity versus the MFP relationship. (b) The scattering rates， (c) the group velocity， and (d) the Raman spectra in multilayer (GaN)1-x(ZnO)x. (e) The scattering-rate distributions of each phonon branch in P3m1-(GaN)1(ZnO)2 with the Born effective charges and the dielectric constants in the first Brillouin zone. (f) The aao scattering channels of (q1，v1)→(q2，v2)+(q3，v3)in the first Brillouin zone in P3m1-(GaN)1(ZnO)2，where q1=(0.0，0.0，0.0)，v1=3.45A1，and v2 and v3 run over the acoustic branches，together with the sketch of the scattering processes of 3.45A1 →LA+TA.

The scattering rates inP3m1-(GaN)1(ZnO)2are at least 50 times higher than at other stoichiometries (see Fig. 3(b))，which finally results in the ultralowκL， although thevλandCvare overall comparable， even slightly larger inP3m1-(GaN)1(ZnO)2(see Fig. 3(c) and Table S3). Another result of huge scattering rates is that theκLwell obeys the～1/Ttrend according to the Bose distributionn0λ=(exp[(Eλ-EF)/kBT]-1)-1.[55]Figure 3(b)also reveals that，inP3m1-(GaN)1(ZnO)2，the phonon scattering mainly occurs at low frequency， which indicates the decisive contributions from the acoustic modes to theκL.

To deeply explore the anomalous scattering inP3m1-(GaN)1(ZnO)2， the Raman spectra are plotted together in Fig. 3(d) for comparison. The in-plane vibrational mode shares a smaller Raman frequency(～3.45 THz)than the outof-plane mode inP3m1-(GaN)1(ZnO)2， while the opposite is true at other stoichiometries(see Fig.S4). Note that 3.45 THz is the phonon frequency of the third optical branch at theΓpoint with theA1representation (labeled as the 3.45A1mode in Fig.S1). The red shift of in-plane Raman peak arises from the high symmetry of theC3vpoint group， which strengthens the in-plane interaction， and thus the in-plane collective vibrational mode phonons 3.45A1are more easily activated due to the relatively weaker out-of-plane interaction， thereby the in-plane mode 3.45A1downshifts.P3m1-(GaN)1(ZnO)2prefers the perfectly planar hexagonal configuration with the AA stacking， where each atom is fourfold coordinated， but not by the conventionalsp3tetrahedrons. One surface layer is purely composed of the Ga–N bonds and another of the Zn–O bonds， with the bond angles of 120°. Thereby each atom locates at the equilibrium position，which effectively suppresses in-plane vibrations.

The scattering channels are greatly activated for the acoustic branches by the down-shift of in-plane optical 3.45A1mode inP3m1-(GaN)1(ZnO)2(see Fig. 3(e))， thereby the phonon population significantly increases at low frequency，which greatly enlarges the phase space and finally reduces theκL. However， at other stoichiometries， the scattering mainly originates from the high-frequency optical modes(see Figs.S5–S7).Figure 3(f)emphasizes on the three-phononaaoscattering channels of (q1，v1)→(q2，v2)+(q3，v3) inP3m1-(GaN)1(ZnO)2. As the phonon frequency increases， the scattering zone shifts from theKpoint of the FA branch to theΓof the 3.45A1branch (see Fig. 3(e))， thereby theq1is fixed to(0.0，0.0，0.0)andv1=3.45A1. As a result，the distributions of the FA， TA， and LA branches are perfectly symmetrical in the Brillouin zone to keep the momentum conservation，i.e.，q2=-q3. The low-frequency scattering rates are dominated by the 3.45A1→LA+LA， 3.45A1→TA+LA， and 3.45A1→FA+LA channels in sequence.

The low lattice thermal conductivityκLusually results in an excellent thermoelectric performance. TheZT versusthe carrier concentration and temperature along the armchair and zigzag directions are plotted in Fig. 4， which displays the obvious asymmetry for p- and n-type dopings. InP3m1-(GaN)1(ZnO)2，the maximumZTis 3.08 along the armchair direction at 900 K for a p-type doping concentration of 0.15×1015cm-2. TherebyP3m1-(GaN)1(ZnO)2is a promising thermoelectric material at medium temperature by properly doping.

Fig.4. Figure of merit ZT along the armchair and zigzag directions versus the carrier concentration and temperature.

TheZTis determined by the power factorPF=σS2，the electronic thermal conductivityκeand the lattice thermal conductivityκL. According toS=8π2k2Bm*T/(2eh2)(π/3n)2/3，the predominant Seebeck coefficientSalong the armchair and zigzag directions favors the highPFand arises from the large effective massm*inP3m1-(GaN)1(ZnO)2(see Fig. S8 and Table 2). This is consistent with the nearly flat top valence band， since the VBM is composed of the fully localized Npzstates， the details are displayed in Fig. 2(e). On the other hand， the low electric conductivityσalong the armchair direction seriously reduces thePF， and then theZT， inP3m1-(GaN)1(ZnO)2(see Figs. S8 and S9). Although a relatively lowκealong the armchair direction for the p-type doping prevents theZTto further drop (see Fig. S10)， the ultralowκLeventually results in the ultrahighZTinP3m1-(GaN)1(ZnO)2.Note that the maximumPFappears inPm-(GaN)3(ZnO)1along the armchair direction for the p-type doping， which favors the highZT， but the relatively largeκeandκLsuppress the thermoelectric performance. Therefore， the phonon contributions are usually more dominant than the electronic contributions in the thermoelectric performance.

Table 2. Carrier mobility μ (in units cm2/V·s) at 300 K and effective mass m* (m0) in Pm-(GaN)3(ZnO)1， Pmc21-(GaN)1(ZnO)1， P3m1-(GaN)1(ZnO)2，and C2/m-(GaN)1(ZnO)3.

Our next focus is the molecular adsorption/permeation capabilities inAA-stackingPm-(GaN)3(ZnO)1，P3m1-(GaN)1(ZnO)2， andC2/m-(GaN)1(ZnO)3. Figure 5(a)shows the energy profilesversusthe relative positions of the H+，Na+， and OH-ions to the multilayer configurations. To realize the permeation， the structural models are constructed as the sketch of Fig. 5(b). The diameters of the hexagonal-ring pores are～3.7 ˚A，thus the H+，Na+，and OH-ions can permeate through the multilayer structures if only the ionic sizes are considered. This is the case for H+ion. However， the Na+ion is only adsorbed near the multilayer surfaces with at least 2.28-˚A distance and the energy well is deeper than-24.0 kcal/mol (see Fig. 5(c)). Surprisingly， the OH-adsorption does not occur. The sketch of H+， Na+， and OHdistributions with respect to multilayer GaN–ZnO is plotted in Fig.5(d).

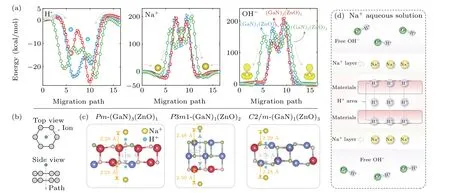
Fig. 5. (a) Energy profile of H+， Na+， and OH- ions along the minimum migration path through the hexagonal ring in Pm-(GaN)3(ZnO)1， P3m1-(GaN)1(ZnO)2， and C2/m-(GaN)1(ZnO)3. (b) Sketch of the ionic position with respect to multilayer structures. (c) Configurations of the H+ and Na+potential wells. (d)Sketch for the molecular permeation of Na+ aqueous solution.

The permeation is determined by the pore diameter， the interaction between the ion and the multilayer structure， and the ionic size. Because of the electron distribution in the inner hexagonal ring(see the ELF in Fig.1)，the Coulomb attractive interactions of H+and Na+ions result in the potential wells near both surfaces，while the Coulomb repulsive force pushes the OH-ion away from the surface.Furthermore，the potential barrier between adjacent adsorption states actually determines the permeation of H+and Na+ions. The Na+radius is relatively large，and thus introduces the huge deformation energy once it is placed in the multilayer structures， which greatly raises the barrier over 200 kcal/mol， thereby the permeation impossibly occurs at ambient condition. On the contrary， the H+barriers are always lower than 8.0 kcal/mol because of its almost negligible radius， thereby it is easy for the H+ion to jump from one adsorption state to another across the barrier zone. The similar results are obtained in the energy profiles of Li+and Be2+ions in Fig. S11. Note that the OH-and Na+ions share very close energy barriers due to the similar ionic sizes.

4. Conclusion

In summary， inspired by the structural anharmonicity， we focus on the effects of the interlayer interactions on the thermal transport， thermoelectrics， electronic structure， and ionic adsorption/permeation in multilayer(GaN)1-x(ZnO)x. The structural searches identify stablePm-(GaN)3(ZnO)1，Pmc21-(GaN)1(ZnO)1，P3m1-(GaN)1(ZnO)2，andC2/m-(GaN)1(ZnO)3. In theP3m1-(GaN)1(ZnO)2， the 3.45A1→LA+LA，3.45A1→TA+LA，and 3.45A1→FA+LA channels dominate the low-frequency scattering，which results in the ultralow thermal conductivity and thereby the ultrahigh thermoelectrics. The anomalous band structure versus ZnO composition inC2/m-(GaN)1(ZnO)3arises from the forbidden N:3p–Zn:3dcoupling according to the group theory. Finally， the potential wells and barriers are deeply explored from the Coulomb interaction and the ionic size to reveal what kinds of ions permeate through multilayer structure. This study provides a new insight into the thermal transport， thermoelectrics， electronic structure， and ionic adsorption/permeation in novel multilayer(GaN)1-x(ZnO)xconfigurations.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 11774416)， the Fundamental Research Funds for the Central Universities (Grant Nos. 2017XKZD08 and 2015XKMS081)， the Postgraduate Research&Practice Innovation Program of Jiangsu Province，China (Grant No. KYCX202039)， and the Assistance Program for Future Outstanding Talents of China University of Mining and Technology(Grant No.2020WLJCRCZL063).