THz wave generation by repeated and continuous frequency conversions from pump wave to high-order Stokes waves

Zhongyang Li(李忠洋)， Qianze Yan(颜钤泽)， Pengxiang Liu(刘鹏翔)， Binzhe Jiao(焦彬哲)，Gege Zhang(张格格)， Zhiliang Chen(陈治良)， Pibin Bing(邴丕彬)，Sheng Yuan(袁胜)， Kai Zhong(钟凯)， and Jianquan Yao(姚建铨)

1College of Electric Power，North China University of Water Resources and Electric Power，Zhengzhou 450045，China

2Shenyang Institute of Automation，Chinese Academy of Sciences，Shenyang 110016，China

3College of Precision Instrument and Opto-electronics Engineering，Institute of Laser and Opto-electronics，Tianjin University，Tianjin 300072，China

Keywords: THz wave generation，optimized cascaded difference frequency generation，aperiodic periodically poled lithium niobate

1. Introduction

In the last two decades， THz science and technology have gained great developments and widely used in biomedicine，[1–3]communications，[4–7]security check，[8，9]THz spectroscopy，[10，11]THz imaging，[12–14]etc. Cascaded difference frequency generation(CDFG)for THz wave generation is a promising method，which can exceed single-photon conversion efficiency.[15–18]However，two problems should be solved for further improving the optical-to-THz energy conversion efficiency (OTECE). Firstly， a large amount of pump photons are not converted to Stokes photons. Two input pump waves and generating Stokes waves pass through optical crystal only once，and the above optical photons are not repeatedly converted into the high-order Stokes photons. Secondly，loworder Stokes photons are difficult to be converted to high-order Stokes photons because phase mismatches are very large especially in high-order cascaded Stokes processes (CSPs).[15，17]Furthermore， THz photons generated by CSPs are consumed by cascaded anti-Stokes processes (CASPs)， which further depresses the OTECE.[16]In this work， we introduce a new scheme for THz wave generation with a high OTECE. The scheme solves the above first problem by setting a resonant cavity (RC) for cascaded Stokes waves (CSWs) where loworder Stokes waves(LSWs)are repeatedly converted to highorder Stokes waves (HSWs). The scheme solves the above second problem by optimized cascaded difference frequency generation (OCDFG) where the phase mismatches of CDFG are optimized.

2. Theoretical model

Figure 1(a) is the structural drawing of the proposed scheme. The Bow-tie RC is composed of four cavity mirrors C1， C2， C3and C4， which is used in Ref. [19]， and the optical crystal is aperiodic periodically poled lithium niobate(APPLN). C1and C2are two concave mirrors， while C3and C4are two plane mirrors. C1is manufactured with a high transmittance at pump wave(ω0)，signal wave(ω1)，and a high reflectivity at CSWs.C2and C3set reflecting more than 99.9%for all optical waves. C2is specially manufactured with silicon， which transmits THz wave with a small absorption. C4has a high transmittance atω0，ω1and anti-Stokes waves，and has a high reflectivity at CSWs. The specialized fabrication of C1and C4has been described by Ito.[20]The above cavity mirrors ensure that pump wave， signal wave， THz wave and anti-Stokes waves do not oscillate within the RC， while only the CSWs oscillate within the RC.

In Fig.1(b)，ω0，ω1and THz wave(ωT)satisfy the firstorder phase matching. As long as phase mismatches of CDFG are not large enough， a series of CSWs and THz photons are generated through the CSPs.Simultaneously，CASPs in which THz photons are consumed and a series of cascaded anti-Stokes waves (CASWs) are generated are stimulated. In this work，ωm(mis an integer)is CSWs withm ＞1 and CASWs withm ≤-1， respectively. The CSWs oscillate within the cavity，so the frequency conversions among Stokes waves are repeatedly performed. The CASWs are not retained in the resonator， which limits the energy transfer fromω0to the CASWs.

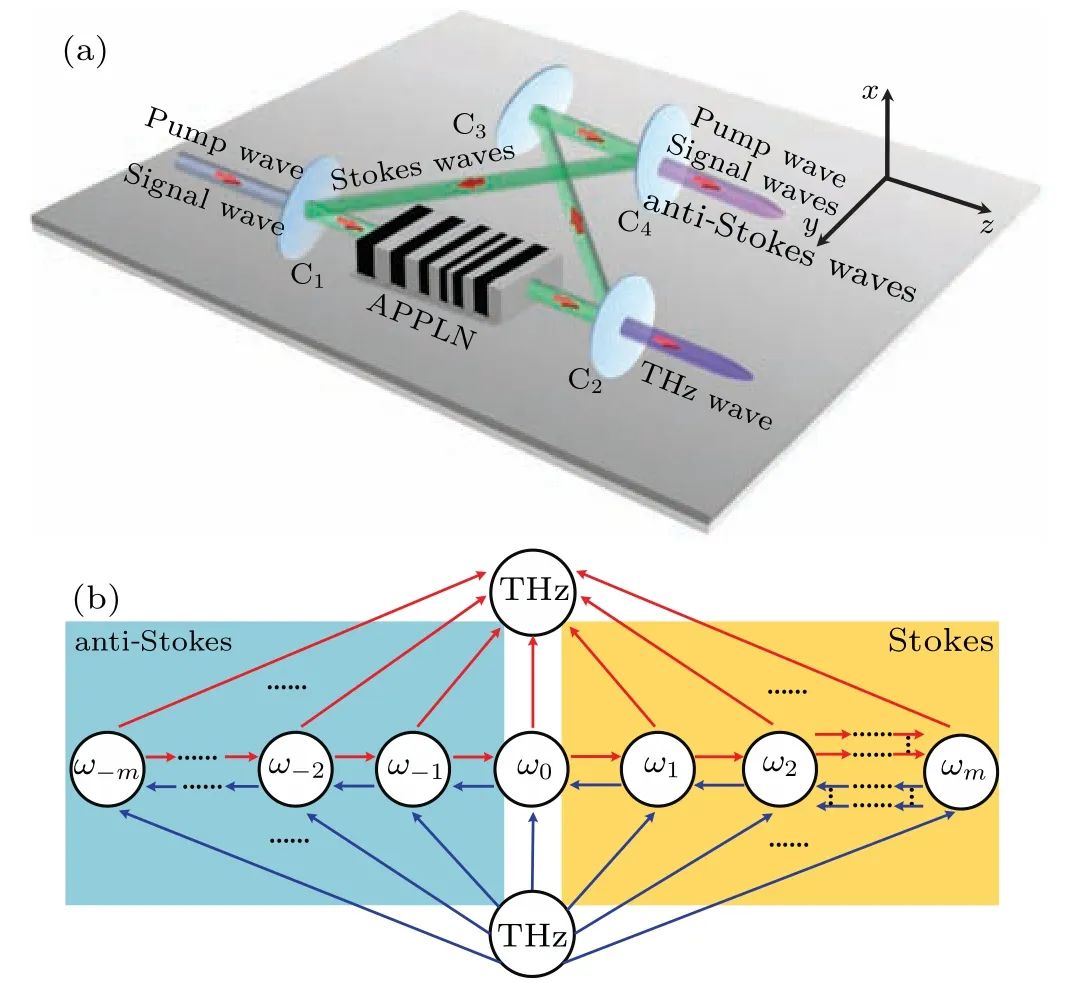
Fig. 1. (a) Schematic diagram describing THz wave generation by OCDFG and the oscillations of Stoke waves in a bow-tie cavity. C1，C2， C3 and C4 are cavity mirrors. (b) Principle diagram of CSPs and CASPs.

Coupled wave equations of CDFG are reported in Ref. [15]. Different from CDFG， CSWs oscillate within the RC in this work. At each time CSWs interact in APPLN crystal， THz wave is generated and coupled out from RC. Combined the coupled wave equations of CDFG with the theory of optical parametric oscillation，we deduce the coupled wave equations which describes the interactions of CSWs，CASWs，and THz wave，given by

whereωandΩare the frequency and angular frequency， respectively，αis the absorption coefficient，κis the coupling coefficient，kis the wave vector，nis the refractive index，and the subscriptsmand T representmth-order cascaded wave andωT，respectively.Eis the electric field strength，Δkrepresents the phase mismatch，cis the vacuum speed of light，ε0represents the vacuum permittivity，Irepresents the intensity， andΛrepresents the poling period of the APPLN.R1andR2are the reflectance of C1and C2， respectively.Pis the oscillation number of Stokes waves，andηrepresents the OTECE.In Eq. (1)， the first item indicates absorption ofωTand the second item indicates the interaction of cascaded waves to generateωT. In Eq.(2)， the first item indicates absorption of the cascaded waves，and the second item indicates the generation and consumption of cascaded waves.

3. Calculations

In this work， the pump frequencyω0is 291.5 THz， the signal frequencyω1is 291 THz， and the generated THz frequencyωTis 0.5 THz. The calculation of the refractive index of MgO:LiNbO3crystal in the near-infrared[21]and THz[22]regions is given by the Sellmeier equation. The nonlinear optical coefficient of the MgO:LiNbO3crystal is 336 pm/V.[15]At 100 K， the absorption coefficient is 0 cm-1for cascaded optical waves and 2.10 cm-1forωT.[22]At 300 K， the absorption coefficient is 0 cm-1for cascaded optical waves and 7.20 cm-1forωT.[23]The laser induced damage threshold of APPLN with sub-nanosecond is about 10 GW/cm2.[15]R1andR2are 0.9999 for CSWs and 0 forω0，ω1and CASWs. The frequency range of theωmis set to 60–500 THz. As shown in Fig. 1(a)， the pump and signal waves do not oscillate within the cavity， so the energies of pump and signal waves should be rapidly transferred to Stokes waves firstly，and then further transferred to HSWs. To realize the above anticipation， the APPLN crystal is designed to be two parts，part I and part II.The poling period distributions in part I are given by

where 0＜z ＜L1，L1is the length of part I，andLis the total crystal length.M1=m-0，m ＞1. Equation(8)leads the Δkmto be zero step by step fromω0toωm(m ＞1)，which accelerates the frequency conversions from LSWs to HSWs uninterruptedly and unidirectionally. The poling period distributions in part II are given by

whereL1＜z ＜L.M2=mf，m ＞1 andf ＜0 (fis an integer).ωfrepresents the CASWs with the highest intensity generated by part I. Equation (9) leads the Δkmto be zero step by step fromωftoωm(m ＞1)， which accelerates frequency transformation from the anti-Stokes waves with the highest intensity to HSWs. In Eqs. (8) and (9)，M1andM2which represent the cascading orders from pump frequency or anti-Stokes frequency to high-order Stokes frequency，respectively，are determined by the pump and signal intensities. Figure 2 shows poling period distributions and phase mismatches Δkmwith different pump and signal intensities at 100 K. As shown in Figs. 2(a) and 2(b)， whenIp=Is=3 MW/cm2，ΛIchanges from 237.18 μm to 236.76 μm andΛIIchanges from 237.22 μm to 236.77 μm， corresponding to the phase matching of CSPs one order by one order from the first order cascaded Stokes process (CSP) to the 20th order CSP in part I and from the first order cascaded anti-Stokes process(CASP)to the 39th order CSP in part II. As shown in Figs. 2(a) and 2(c)，whenIp=Is=3 MW/cm2，ΛIchanges from 237.18 μm to 236.55 μm andΛIIchanges from 237.34 μm to 235.76 μm，corresponding to the phase matching of CSPs one order by one order from the first order CSP to the 40th order CSP in part I and from the third order CASP to the 147th order CSP in part II. As shown in Figs. 2(a) and 2(d)， whenIp=Is=300 MW/cm2，ΛIchanges from 237.18 μm to 236.36 μm andΛIIchanges from 237.49 μm to 234.54 μm，corresponding to the phase matching of CSPs one order by one order from the first order CSP to the 54th order CSP in part I and from the ninth order CASP to the 291th order CSP in part II.ΛIandΛIIare different with different pump and signal intensities.This is because the speed of photon transfer from themth-order to the(m+1)th-order Stokes wave depends on the pump and signal intensities. As the pump and signal intensities increase， the variation ofΛIandΛIIis fast and the crystal length is shortened.

Fig. 2. Poling period distributions and phase mismatches Δkm with different pump and signal intensities at 100 K. L=2×L1. Ip =Is =3 MW/cm2， ωf =292 THz， M1 =20， M2 =40; Ip =Is =30 MW/cm2， ωf =293 THz， M1 =40， M2 =150; Ip =Is =300 MW/cm2，ωf =296 THz，M1 =54，M2 =300. (a)Poling period distributions，(b)Δkm with Ip =Is =3 MW/cm2，(c)Δkm with Ip =Is =30 MW/cm2，(d)Δkm with Ip=Is=300 MW/cm2.

Fig.3. THz wave intensities and cascaded optical spectra generated by OCDFG in combination with the oscillations of Stoke waves at 100 K.(a)THz wave intensities with Ip =Is =3 MW/cm2，(b)THz wave intensities with Ip =Is =3 MW/cm2，(c)THz wave intensities with Ip =Is =30 MW/cm2，(d)cascaded optical spectral evolution corresponding to(a)， (e)cascaded optical spectral evolution corresponding to(b)， (f)cascaded optical spectral evolution corresponding to(c)，(g)energy distributions of THz wave and cascaded optical waves within the APPLN crystal with P=200 corresponding to (a)， (h) energy distributions of THz wave and cascaded optical waves within the APPLN crystal with P=200 corresponding to (b)， (i) energy distributions of THz wave and cascaded optical waves within the APPLN crystal with P=200 corresponding to(c).

The intensities ofωTand the spectral evolution resulting from OCDFG in combination with the oscillations of Stoke waves at 100 K are calculated， as shown in Fig. 3. In Figs.3(a)–3(c)the anti-Stokes region is above the dashed line and the Stokes region is below the dashed line. The pump and signal photons are converted to high-order Stokes photons one order by one order with the increase of oscillation numberP.At each oscillation numberPthe photons are accumulated to few cascaded optical frequencies. WithIp=Is=3 MW/cm2the energy transfer is slow and the pump photons are not converted to 60 THz， while the energy transfer is rapid and the pump photons are converted to 60 THz atP=140 withIp=Is=300 MW/cm2. From Figs.3(d)–3(f)we find that cascaded optical spectral evolution is rapid with the oscillation numberP. The cascaded optical spectra comprise only a few frequency components. The above results inspire us to generate mid-infrared laser by the novel scheme proposed in this work. Figures 3(g)–3(i) show energy distributions within the APPLN crystal withP=200. The intensity of each cascaded optical wave is constant， while the intensity ofωTincreases rapidly with the crystal length. The maximumωTintensities of 0.22 MW/cm2，9.89 MW/cm2，and 260.2 MW/cm2are realized when both the pump and signal intensities are 3 MW/cm2，30 MW/cm2and 300 MW/cm2，respectively.

Cascaded optical waves intensities generated by OCDFG in combination with the oscillations of Stoke waves at 300 K are calculated，as shown in Fig.4. The pump and signal photons spread rapidly to the HSWs. Compared with Figs.3(a)–3(c)，the spectral evolution range at 300 K is smaller than that at 100 K with the same inputs. This is because the absorption coefficient ofωTat 300 K is much larger than that at 100 K， which in turn weakens the OCDFG process. Therefore，the values ofM1andM2at 300 K are smaller than those at 100 K.Figure 5 shows the OTECE corresponding to Figs.3 and 4，respectively.When both the pump and signal intensities are 3 MW/cm2， 30 MW/cm2and 300 MW/cm2， the OTECE reaches 0.12%，7.65%and 26.57%at 300 K respectively，and reaches 3.73%，16.49%and 43.37%at 100 K respectively.The higher the pump intensity stimulated， the higher the OTECE obtained. OTECE exceeding 40%at 100 K indicates thatωTare efficiently generated by repeated and continuous frequency conversions fromω0to HSWs in the cavity.

Fig.4. Cascaded optical spectra generated by OCDFG in combination with the oscillations of Stoke waves at 300 K.(a)Ip=Is=3 MW/cm2，ωf =292 THz， M1 =20， M2 =20 and L=50 mm. (b) Ip =Is =3 MW/cm2， ωf =292 THz， M1 =20， M2 =100 and L=8 mm， (c)Ip=Is=300 MW/cm2，ωf =293 THz，M1=28，M2=175 and L=3 mm.

Cascaded optical waves intensities generated by OCDFG without RC at 100 K are calculated， as shown in Fig. 6. The pump and signal photons simultaneously spread to the Stokes and anti-Stokes region. At each pump intensity， a large portion of photons are converted into anti-Stokes region， which consumes THz photons and reduces the OTECE. Moreover，the cascaded Stokes frequency cannot reach 60 THz. Without repeated frequency conversions fromω0to HSWs， OCDFG cannot substantially compress the CASPs. As a result， intensity ofωTgenerated by OCDFG without RC is significantly suppressed.

Fig.5. OTECE at 100 K and 300 K，respectively.

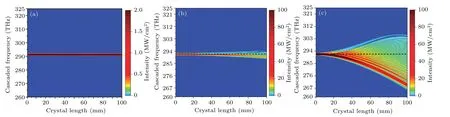
Fig.6. Cascaded optical spectra generated by OCDFG without RC.The anti-Stokes region is above the dashed line and the Stokes region is below the dashed line. (a)Ip=Is=3 MW/cm2，(b)Ip=Is=30 MW/cm2，(c)Ip=Is=30 MW/cm2.

4. Discussion

Recently，THz wave generations by THz wave parametric oscillator (TPO)，[24]difference frequency generation(DFG)，[25]and CDFG[18]develop rapidly. For the scheme of TPO， noncollinear phase-matching configuration restricts the interaction volume of mixing waves and depresses the photon conversions from pump wave to THz wave. Jiaet al.reported a TPO generating THz waves with a KTiOPO4crystal. When the incident Stokes pulse energy was 36.6 mJ and the pump energy was 580.0 mJ， the obtained maximum THz wave energy was only 17.0 μJ and the quantum efficiency was below 1%.[26]For the scheme of DFG， one pump photon can generate one THz photon at most. Satoet al.reported a DFG scheme generating THz waves with a 2D InxGa1-xSe crystal.The maximum energy of the generated THz wave was 39 pJ and the conversion efficiency was only 1.7×10-5J-1.[27]CDFG is a promising method to generate numerous THz photons from a single pump photon. Raviet al.reported a theoretical work generating THz wave with CDFG under broadband phase matching conditions.[18]The maximum OTECE of 35%was realized at 10 K.Compared with the Ravi’s work，though the absorption coefficients for 0.5 THz at 100 K and 300 K are 8.4 times and 28.8 times higher than that at 10 K respectively， the maximum OTECE of 26.57% at 300 K and 43.37% at 100 K in our work are realized. Compared with the schemes of TPO， DFG and CDFG， the high OTECE in this work is originated from the usage of APPLN in combination with the oscillations of Stoke waves，which can efficiently boost the generation of THz wave by repeated and continuous energy conversions from pump wave to HSWs.

The scheme in this work is practically feasible. Experimental equipment mainly consists of four cavity mirrors， a specially manufactured APPLN crystal and two pump lasers.The fabrication technology of the cavity mirrors has been reported by Ito in 2006. APPLN crystal has been widely utilized for mid-infrared and THz wave generations.[28，29]The Yb:YAG laser with 1030 nm wavelength can be employed as the pump lasers. The intensities of 300 MW/cm2，3 MW/cm2and 3 MW/cm2can be provided by pulsed， quasi-continuous and continuous Yb:YAG lasers respectively，so pulsed，quasicontinuous and continuous THz waves can be generated with the scheme in this work.

5. Conclusions

We introduce a new scheme for high-efficiencyωTgeneration by OCDFG in combination with the oscillations of Stokes waves. We find that oscillations of Stoke waves rather than other optical waves can repeatedly transfer energies fromω0to HSWs， and the modulation of phase mismatches of cascaded optical processes can continuously transfer energies fromω0to HSWs.Combined with OCDFG and oscillations of Stokes waves the OTECE exceeds 26%at 300 K and 43.37%at 100 K with the pump intensities of 300 MW/cm2. The new scheme proposed in this work provides an effective technique to generate pulsed，quasi-continuous or continuous THz waves.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 61735010， 31671580， and 61601183)， Natural Science Foundation of Henan Province，China (Grant No. 162300410190)， and Program for Science&Technology Innovation Talents in Universities of Henan Province，China(Grant No.18HASTIT023).