Spatio-spectral dynamics of soliton pulsation with breathing behavior in the anomalous dispersion fiber laser

Ying Han(韩颖)， Bo Gao(高博)，†， Jiayu Huo(霍佳雨)， Chunyang Ma(马春阳)， Ge Wu(吴戈)，Yingying Li(李莹莹)， Bingkun Chen(陈炳焜)， Yubin Guo(郭玉彬)， and Lie Liu(刘列)

1College of Communication Engineering，Jilin University，Changchun 130012，China

2Collaborative Innovation Center for Optoelectronic Science&Technology，Key Laboratory of Optoelectronic Devices and Systems of Ministry of Education and Guangdong Province，Institute of Microscale Optoelectronics，Shenzhen University，Shenzhen 518060，China

3College of Electronic Science and Engineering，Jilin University，Changchun 130012，China

Keywords: soliton pulsation，dispersive Fourier transform，numerical simulation，breathing behavior

1. Introduction

In recent decades， researchers’ enthusiasm for passively mode-locked fiber lasers (PMFLs) has not diminished.[1–3]Due to the dissipative properties of such fiber lasers， solitons can change their shapes，amplitude，and pulse width regularly under the adjustment of system parameters， which is called soliton pulsation. As a unique local structure in the fiber laser， soliton pulsation has been paid much attention by researchers. Although soliton period-doubling bifurcation[4]and multi-period pulsation[5]have been observed in nonlinear polarization mode-locked fiber lasers as early as 2004，due to the lack of experimental instruments capable of capturing real-time spectra of solitons， the research on soliton pulsation was mainly based on theoretical analysis and simulation analysis. For example， researchers have used a complex cubic-quintic Ginzburg–Landau equation (CQGLE) to study pulsating，[4]creeping，[5]and erupting solitons[6]in fiber lasers.[7]And the soliton pulsation with breathing behavior was studied by the CQGLE[8，9]in recent years. At the same time， researchers have used a simpler nonlinear Schr¨odinger equation (NLSE)[10]to study the Akhmediev breathers that show similar breathing behavior to soliton pulsation. And the Ginzburg–Landau equation (GLE)[11，12]can be used to observe the breathing behavior of soliton pulsation in a fiber laser mode-locked by the nonlinear polarization rotation (NPR)technique. Modeling fiber lasers based on such two equations is closer to actual fiber lasers and deserves more in-depth research.

The dispersive Fourier transform (DFT) technique is a new way to study the real-time spectral of the soliton.[13]The soliton spectrum is mapped to the time waveform by employing dispersive elements that have large group velocity dispersion. Therefore， people can obtain the ultrafast spectrum through the real-time oscilloscope together with the high-speed photodetector. A variety of soliton transient dynamics was observed in passively mode-locked fiber lasers adopting the DFT technique: the build-up of dissipative soliton pulsation，[14]successive soliton explosion，[15]explosion induced rogue waves.[16]Breathing behavior of dissipative soliton pulsation，[17–19]multiple soliton pulsation，[20，21]dissipative soliton explosion[22]and the pulsating soliton molecule[23]are observed in the normal dispersion NPR mode-locked fiber laser by the DFT. In the anomalous dispersion region，the soliton pulsation with chaotic behavior[24]and the soliton pulsation sideband characteristics[12]are also studied. However， there are few studies on soliton pulsation with breathing behavior in anomalous dispersion NPR modelocked fiber lasers. It is found in references[25–27]that the soliton pulsation has obvious breathing behavior in the real-time spectral evolution.

In this research， the breathing behavior of soliton pulsation in anomalous dispersion NPR passively mode-locked fiber laser is studied by numerical simulation and experiment.Specifically， we studied the influence of the phase difference caused by the polarization controller on the breathing period of soliton pulsation through theoretical modeling of such fiber lasers. At the same time，we obtained the single-shot spectral evolutions of the soliton pulsation via the DFT technique to further explore the breathing behavior in the experiment. The breathing behavior is achieved by adjusting the polarization controller. It has similar features such as energy oscillation and bandwidth breathing to simulation results.

2. Physical model and DFT technique

2.1. Physical model of the passively mode-locked fiber laser

The pulse tracing technique can numerically simulate the pulse evolution in PMFLs. Such a method takes into account the effect of each element in the fiber laser on the light field.All the components in the laser are successively distributed in the laser cavity. Figure 1 is the physical model of the typical PMFL. The doped fiber usually includes Er-doped fibers(EDF)，Yb-doped fibers(YDF)，Tm-doped fibers(TDF)，Hodoped fibers， etc. The undoped fiber usually contains singlemode fibers (SMF)， dispersion compensation fibers (DCF)，etc. Saturable absorber(SA)mainly includes artificial SA and real SA. Researchers used the NLSEs to calculate the transmission of pulses in undoped fibers and the GLEs to calculate the transmission of pulse in the doped fiber. When the pulse passes through other components，such as SA and output coupler (OC)， the Jones matrix equation of the component is directly multiplied by the light field to represent its influence on pulse transmission. In the simulation， the initial input signal is arbitrary. When the pulse runs in the cavity for one roundtrip (RT)， the result is regarded as the next RT input pulse.Using the pulse tracing method for numerical simulation can observe the output pulse at any time and any position in the cavity，the evolution process of the pulse，and the influence of each element on the pulse evolution， which is impossible in the experiment.

2.2. Introduction of DFT technique

The DFT technique is based on the analogy between spatial Fraunhofer diffraction and time dispersion: the diffraction of the light beam in the far-field through the lens is analogous to the transmission of pulse in the dispersive element，which is also called spatiotemporal duality. Figure 2 is the schematic diagram of the DFT technique. The DFT system consists of the dispersive element with large group velocity dispersion， photodetectors， and a real-time digital oscilloscope: the pulse is stretched due to the large group velocity dispersion of dispersion element when there is pulse transmission in it. After being stretched， the soliton intensity envelope has the same shape as the spectrum; that is， the soliton spectrum is mapped to its time profile to realize the timedomain measurement of the soliton spectrum. Such a timedomain stretched pulse is obtained via the high-speed photodetector，therefore，the single-shot spectrum information can be observed and analyzed through the real-time digital oscilloscope.There are many kinds of dispersive components used in the DFT technique，including SMF，DCF，chirped fiber Bragg grating，multi-mode waveguide，etc.In the DFT technique，the spectrum detection speed can reach the same level as the repetition frequency of the mode-locked lasers and can realize the measurement and observation of a single real-time spectrum.Using this technique， researchers have a better understanding of the physical mechanism of various soliton transient dynamics， which has important implications for optimizing the performance of fiber lasers and promoting basic research in the field of fiber lasers.

Fig.2. Schematic diagram of the DFT technique.

3. Numerical simulation results

3.1. Simulation model

Figures 1 and 5 are the simulation schematic and the experiment schematic of anomalous dispersion NPR passively mode-locked fiber laser， respectively. It consists of the EDF，SMF， NPR as the saturable absorber， and an OC. The OC is utilized to extract 40% of the intracavity pulse energy for decreasing intracavity nonlinearity and avoiding excessive pulses. As shown in Fig.5，two PCs，an isolator，and birefringent fiber constitute the NPR.The pulse with any polarization state becomes linearly polarized after passing through the isolator. When it propagates in the fiber， it will split into two orthogonal elliptical polarization components along the two main axes of the fiber. Due to the influence of the nonlinear effects of the fiber，the polarization state of the pulse will undergo intensity-related evolution when it is transmitted in the fiber. As the pulse passes through the NPR，the low-intensity wings of the pulse are absorbed， and the high-intensity center passes smoothly. The pulse will be narrowed slightly after an RT in the cavity，and it will be significantly narrowed after multiple RTs.

Since NPR is related to the birefringence effect of the fiber，our simulation is based on coupled GLE(in doped fiber)and coupled NLSE(in single-mode fiber)，which can be solved via the symmetric split-step Fourier method. The coupled GLE is expressed as follows:

whereuandvdenote the envelopes of the optical pulses，which propagates along the two orthogonal polarization axes of the optical fibers. 2β=2πΔn/λrepresents the wavenumber difference between the two orthogonal polarization modes， and 2δ=2βλ/2πcis the reciprocal of the group velocity difference.γis the nonlinear coefficient.β2represents the group velocity dispersion.gis the gain of the fiber given by the spectrally correlated parabolic frequency domain expressiong(ω):

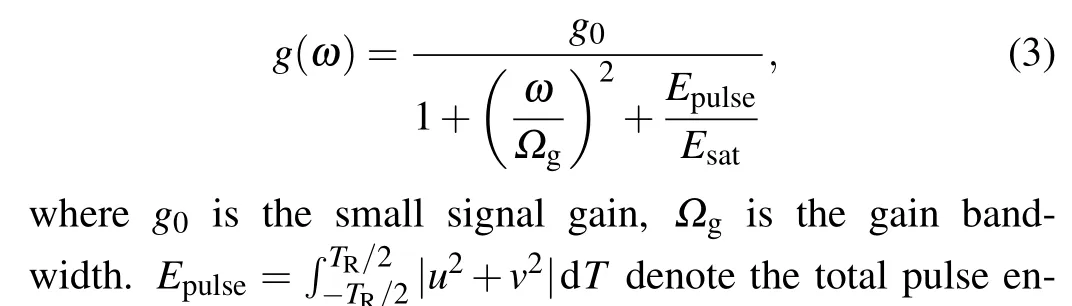
whereθis the angle between the fast axis of the birefringent fiber and the polarizer， andφrepresents the angle between the fast axis of the birefringent fiber and the analyzer. ΔΨL=(2πL/λ)(nx-ny)+ΨPCis the linear phase delay. The phase difference of the pulse caused by polarization controllers (PCs) is represented byψPC.λandLrepresent the light wavelength and the cavity length，respectively.The nonlinear phase delay caused by self-phase modulation and cross-phase modulation can be expressed as ΔΨNL=-(2πLn2P/3λAeff)cos(2θ)， wheren2denotes the nonlinear coefficient.Aeffis the effective mode area，andPis the optical power. In the time domain，this simulation grid consists of 214points. The detailed parameters of our simulation are shown in Table 1.

3.2. Result and discussion

To explore the influence ofψPCon the breathing behavior of soliton pulsation，firstly，we find the stationary soliton with the value of system parameter taken as Table 1， at the same time，takenψPCas 0°. Figures 3(a)–3(a4)includes the correlation graphs of stationary soliton. Figures 3(a)–3(a4) shows that both time-domain and frequency-domain soliton exhibit similar shapes during the evolution，and the energy shows the constant value of 20.2 pJ. Later， we change the value ofψPCto explore its influence on soliton evolution. When it is taken as 7°，6°，3°，the soliton exhibits breathing behavior(the characteristic of soliton pulsation).

Table 1. Parameters of the fiber laser.

Fig.3. Column(a)and column(b)represent the correlation graphs when ψPC=0°and 7°，respectively:[(a)，(b)]time-domain evolution;[(a1)，(b1)]spectral evolution; [(a2)，(b2)]energy evolution of stationary soliton and soliton pulsation; (a3)extracted spectral evolution diagram of(a1); (b3)extracted spectral evolution diagram of one breathing period;(a4)single-shot spectral of stationary soliton;(b4)single-shot spectral for the maximal and minimal bandwidths.

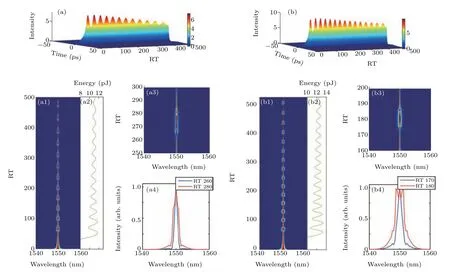
Fig. 4. Column (a) and column (b) represent the correlation graphs when ψPC =6°， 3°: [(a)， (b)] time-domain evolution; [(a1)， (b1)] spectral evolution;[(a2)，(b2)]energy evolution;[(a3)，(b3)]extracted spectral evolution diagram of one breathing period;[(a4)，(b4)]single-shot spectral for the maximal and minimal bandwidths.

Figures 3(b)–3(b4)and 4 show correlation graphs of different soliton pulsation with breathing behavior. It is evident in Figs. 3(b)， 4(a)， and 4(b) that the soliton presents pulsation characteristics;that is，the soliton width and soliton intensity of the soliton change periodically as the increase of RT.As can be seen in Figs. 3(b1)， 4(a1)， and 4(b1)， the soliton spectrum shows breathing behavior， and the breathing period is around 35 RTs(Fig.3(b3))，50 RTs(Fig.4(a3))and 40 RTs(Fig. 4(b3))， respectively. Researchers defined the ratio between the maximum and minimum spectral bandwidth in one period as the breathing ratio. According to Figs.3(b4)，4(a4)，and 4(b4)the breathing ratio is～2.5，～2，and～2.5，respectively. The periodic energy changes during the soliton pulsation dynamics in Figs.3(b2)，4(a2)，and 4(b2)indicate that the gain saturation effect has an impact on the soliton of PMFLs.

Comparing Figs. 3(b)–3(b4) and 4， it can be seen that the angle of the polarization controller may affect the breathing characteristics of the soliton pulsation， including different fluctuations in the time domain evolution， changes in the breathing period and the shape of the spectrum. Since NPR produces saturable absorption characteristics based on intensity-sensitive polarization evolution， its parameters can be determined by the polarizer，nonlinear phase accumulation，and linear phase bias controlled by the polarization controllers.It can also be used as a birefringent filter[30]to achieve wavelength tuning or use its spectral filtering effect to achieve soliton pulsation with breathing behavior.

4. Experimental results

4.1. Experimental setups

We constructed an NPR mode-locked fiber laser as shown in Fig.5 as the test-bed system to verify the above simulation results. The gain medium is 0.7-m EDF，which is pumped by a 976-nm laser source through the wavelength division multiplexer. The parameters of EDF，SMF，and other elements used in the experiment are the same as in Table 1. Therefore， the cavity net dispersion is about-0.13 ps2. The combination of two polarization controllers (PCs) with the polarizationdependent isolator between them produces the saturable absorption effect known as NPR mode-locking. That makes it possible to simply rotate the blades of the PCs to adjust the transmission function of NPR and modify the linear cavity loss and the interaction between pulses. At the same time，we recorded the single-shot spectrum using the DFT technique，in which the frequency-to-time transformation is realized by using 10-km SMF.It is subsequently fed to a 5-GHz photodetector(PD，THORLABS DET08CFC/M)that is connected to a 12.5-GHz real-time oscilloscope (Tektronix DP071254C).The corresponding spectral resolution(in nm)is conveniently expressed as Δλ= (B|D|z)-1[31]whereB= 12.5 GHz is the overall detection bandwidth， andD=-(2πc/λ2)β2=20 ps/(nm·km) is the dispersion parameter，zis the propagation distance. Therefore， in our case， the real-time spectral resolution is about 1 nm.

Fig. 5. Schematic diagram of NPR mode-locked fiber laser for the experiment.

4.2. Result and discussion

By properly adjusting the pump power to the modelocking threshold of about 460 mW and the paddle direction of the PCs， a mode-locked soliton spectrum is observed and shown in Fig.6(b). We employ the DFT technique to further validate the real-time soliton spectrum. The real-time spectral evolution(Fig.6(a))and the evolution process(Fig.6(c))of the soliton show that it has a similar shape， and uniform intensity，indicating that it is a stationary soliton. The stationary soliton has been commonly seen and fully investigated.Nevertheless， the research of soliton pulsation with breathing characteristics is not comprehensive.

Fig.6.(a)Spectrum，(b)real-time spectral and evolution of stationary soliton and(c)the evolution process of the stationary soliton.

Soliton pulsation is related to the nonlinear gain saturation and spectral filtering， so the conversion from stationary to pulsation can be realized by adjusting the pump power. In previous simulations， various pulsation solitons has been observed by changing the intracavity spectral filtering effect.[32]It has been proved that if an in-line polarizer(ILP)[33]is added to the single-wall carbon nanotube(SWNT)mode-locked fiber laser， the spectral profile changes with the adjustment of the intracavity-loss-dependent gain spectrum[34]and the spectral filtering effect.[35]The characteristics of NPR are determined by the polarizer， nonlinear phase accumulation， and PCscontrolled linear phase bias. Adjusting the PCs will change the intracavity total birefringence， which can affect the bandwidth，and the free spectral range of the NPR filter effect，resulting in the soliton pulsation. We have taken pump power at about 460 mW in the experiment，while the only variable is the paddle direction of PCs.

Fig. 7. (a) Real-time spectral evolution of soliton pulsation with breathing behavior; (b) energy evolution; (c) extracted spectral evolution diagram of one breathing period;(d)single-shot spectrum for the maximal and minimal bandwidths;(e)evolution process of soliton pulsation.

The real-time spectral evolution dynamics in Fig.7(a)exhibit similar breathing dynamics in references[25–27]and above simulation. Figure 7(d) shows spectral profiles for the maximal bandwidth and the minimal bandwidth， proving that the breathing ratio is～3.25. The soliton spectrum is continuously compressed and stretched with a period of 2000 RTs(Fig. 7(c)). The energy of the pulse was obtained by integrating the power spectral density over the whole wavelength band， as shown in Fig. 7(b). Pulse energy variation and the evolution process(Fig.7(e))show periodic oscillations corresponding to the change of pulse width， bandwidth， and peak power. And the amplitude of the energy oscillation echoes the spectral breathing ratio. The breathing behavior of the soliton complex in NPR mode-locked fiber lasers was proved in reference，[25]and the experimental results were verified by CQGLE.Our experiment further proves that the single soliton pulsation can also show breathing behavior in the same fiber laser. At the same time，the simple and practical couple GLEs are used to verify breathing behavior which is closer to actual fiber lasers and deserves more in-depth research.

In the simulation， there is little difference between the single-shot spectral for the maximal bandwidth and the minimum bandwidth， and the shape will change slightly. In the experiment， the shape of the spectrum remains almost unchanged， and the intensity of the spectrum changes greatly.The intensity of the maximum spectrum is 2.5 times the minimum spectrum. Usually， the simulation considers the ideal situation such as taking the parameters of gain fiber and the transfer function of the mode-locked device as ideal values，ignoring the influence of fiber loss，environmental factors，etc.However，some factors need to be considered in actual operation， for instance， the influence of temperature on the dispersion value of the gain fiber， the influence of fiber bending on the fiber birefringence， the influence of the loss of the fiber，and other components in the laser cavity on the evolution of soliton，the influence of the loss of fiber and other components in the laser cavity on the evolution of the soliton， the error of the photoelectric detector and oscilloscope in the measurement process will also affect the results. These factors cause the difference between the change of spectral intensity in the experiment and the simulation，which is inevitable.

Pulse temporal duration also varies， and the temporal resolution of existing detection systems cannot capture these changes. A temporal magnifier technique known as time-lens may solve such constraints.[36，37]Nevertheless， the time-lens technique can be difficult to implement when the pulse undergoes large breathing. The time magnifying window is limited by the width of the pump pulse in the time-lens technique，which requires the pump pulse to be synchronized with the signal. When the signal is beyond the magnifying window，the information that can be measured is very limited and sometimes not even available. It is very difficult to study the full field soliton transient dynamics in mode-locked fiber lasers.

5. Conclusion and perspectives

In conclusion， we have experimentally and theoretically investigated the breathing behavior of soliton pulsation in the anomalous dispersion NPR mode-locked fiber laser. Through the model based on the couple GLE and transfer function for NPR， the simulation shows that the breathing characteristics of soliton pulsation can be influenced by the angle of the polarization controller.Subsequently，the breathing behavior of soliton pulsation is observed by continuously adjusting the polarization controller with the dispersive Fourier transform technique in the experiment. The experimental results in this letter qualitatively agree with the numerical results，which demonstrate the couple GLE as a powerful equation to model the behaviors of the fiber lasers. The complex properties of the NPR effects，as well as the complex dissipative properties of fiber laser， result in breathing phenomena in our case even with the fixed pump power. The experimental results are qualitatively consistent with the simulation results，indicating that the couple GLEs are powerful equations to model fiber lasers.In our case，the complex properties of the NPR effect and the complex dissipative nature of the fiber laser cause soliton pulsation even if the pump power remains constant. The limited examples presented above do not fully represent the complex soliton pulsation dynamics. However， these results will appeal to the community dealing with ultrafast lasers and nonlinear optics and better designing ultrafast fiber lasers. Further explanation of the time-domain formation (via the time-lens technique) of the observed soliton pulsations will be the aim of our future work.

Acknowledgments

Project supported by the Jilin Province Science and Technology Development Plan Project， China (Grant Nos. 20190201128JC and 20200401125GX)， the National Natural Science Foundation of China (Grant No. 62105209)，Foundation and Applied Foundation Research Fund of Guangdong Province， China (Grant No. 2019A1515111060)， and Science and Technology Project of the 13th Five-Year Plan of Jilin Provincial Department of Education， China (Grant Nos.JJKH20190157KJ and JJKH20190169KJ).