利用模糊Laplace变换的方法求解模糊分数阶积分微分方程
李慧敏,顾海波
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
模糊性微积分方程中模糊性的概念是模糊分析中的重要组成部分,在数学和应用科学的其他领域也起着关键作用。近年来分数阶微积分在数学的应用方面产生了相当大的影响,被应用于许多物理和化学过程的建模和工程[1-2]。在过去的几十年里,许多研究者探索了模糊分数阶微积分,并在模糊分数阶微分方程和模糊分数阶积分方程中引入了一些新的概念,这些研究成果被用于解决应用数学中的各种问题,如物理、医学、地理、电磁、控制理论和黏弹性等[3-6],其中的变量和参数通常是模糊而非精确的。
由于模糊数空间中的分析学和代数学理论远没有经典理论那样完善,各类导数特别是高阶导数定义复杂烦琐而且条件苛刻,从微分方程到积分方程的等价转换也相对困难,所以研究分数阶模糊微分方程需要可靠的分析方法和高效的数值技术。所以,对分数阶模糊微分方程基本理论和基本性质进行更加深入系统地研究,不仅可以为分数阶模糊微分方程理论的进一步发展奠定坚实的基础,还可以为其他科学领域提供强有力的理论支撑。
本文主要研究具有Caputo分数阶导数的非线性模糊分数阶积分微分方程
(1)
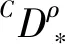
1 预备知识
给出文中所涉及的基本概念、定义、引理和性质,更多的细节可见参考文献[7-14]。
先给出模糊数的定义[7]:用R表示所有实数的集合,R上所有模糊数的集合用E表示。一个模糊数是一个映射v:R→[0,1],具有以下性质:
(1)v是上半连续的;
(2)v是模糊凸的,即对于任意的x,y∈R,λ∈[0,1],满足v(λx+(1-λ)y)≥min{v(x),v(y)};
(3)v是正规的,即∃x0∈R,有v(x0)=1;
(4) suppv={x∈R|v(x)>0},其闭区域cl(suppv)是紧致的。
再给出一个等效的参数定义,如下:
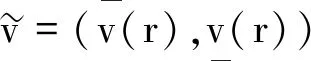
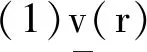

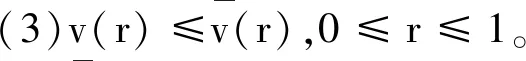

定义3[10]根据Zadeh的扩展原理,RE上的模糊数加法公式和模糊数标量乘法公式分别为

定义4[11]对任意μ,v∈RE,如果存在ω∈RE,使得μ=v⨁ω,则称ω为u和v之间的差,记为ω=μ⊖v。在本文中,⊖表示模糊数差的运算,注意u⊖v≠u+(-v)。
定义5[12]函数f(y)的Riemann-Liouville型分数阶积分定义为
在讨论分数阶模糊微积分之前,首先引入两个符号:CE[a,b]表示区间[a,b]上所有连续模糊值函数的集合;LE[a,b]表示区间[a,b]上所有可测且可积的模糊数值函数的集合。


其中
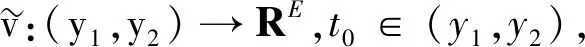





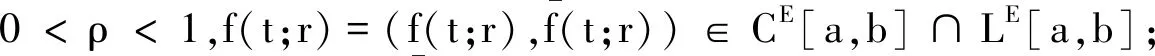
当f是(2)型可微时有
其中[11]
2 模糊Laplace变换与Adomian分解法
2.1 模糊Laplace变换
在本节中,给出模糊值函数的模糊Laplace变换的定义。此外,将考虑模糊Laplace变换的性质,然后给出一个导数定理,以便将分数阶导数的Laplace变换与相应的模糊值函数联系起来。首先,Allahviranloo等[15-16]提出了模糊值函数的Laplace变换,并研究了其一些已知的性质。
定义7函数f(x)(x>0)的经典Laplace变换被定义为
[f(x)]=F(s)=f(x)e-sxdx,
其中s为实数或复数。
定义8[15]模糊函数的模糊Laplace变换为
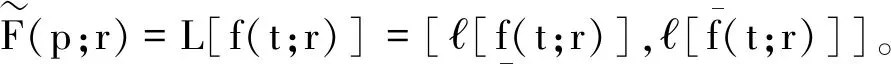
其中
定义9Caputo型导数的Laplace变换[f(x)]为
定理2[15](模糊卷积定理) 假设函数f(t)和g(t)是定义在[0,+∞)的连续的模糊值函数,则
L{f(t)*g(t)}=L{g(t)*f(t)}=L{f(t)}·L{g(t)}。
定理3(导数定理) 假设f∈CF[0,∞)∩LF[0,∞),α∈(0,1]。然后有
L[(CDαf)(t)]=sαL[f(t)]⊖sα-1f(0)。
(1)假设f是C[(i)-α]-可微模糊值函数,则L[(CDαf)(t)]=-sα-1f(0)⊖[-sαL[f(t)]];(2)假设f是C[(ii)-α]-可微模糊值函数,有上式Hukuhara差。
性质1[15]设f和g是连续的模糊值函数,假设c1和c2是常数,则有
L[(c1⊙f(x))⨁(c2⊙g(x))]=(c1⊙L[f(x)])⨁(c2⊙L[g(x)])。
2.2 Adomian分解法
对所研究的Caputo意义下模糊分数阶积分微分方程 (1)两边同时作用Iρ,有
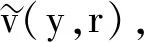
(2)
将非线性项N1和N2分解为
(3)
其中Pn和Qn是Adomian分解,为
因此可以得到

2.3 改进的模糊Laplace变换分解方法
在本节中,通过模糊Laplace变换及其逆变换来推导模糊分数阶微分方程的数值解。根据Caputo分数阶导数算子应用模糊Laplace变换,将模糊Laplace变换应用于方程(1)两侧可以得到
(4)

由引理1和定理3得到
(5)
(6)
将式(6)代入式(4),可以得到
因此,给定的方程等价于
将式(2)(3)代入上式,得到
相似地,有

由引理1和定理3得到
(7)
(8)
将式(8)代入式(4),可以得到
类似于情形1的迭代步骤,可以得出相关结论:
相似地,有
3 例子
利用基于模糊Laplace Adomian 分解法来求解模糊分数阶积分微分方程的近似解。
(9)
采用改进的模糊Laplace Adomian分解方法。将模糊Laplace变换应用于式(9)两侧:
利用模糊Laplace变换的性质和初始条件(9),得到
然后有
将式(2)(3)代入上式,得到
通过将Laplace逆变换应用于上述方程,即可得到模糊分数阶积分微分方程的近似解
根据求出的前三项和的解的形式,由计算机算法得到所得到的近似解的图像,见图1、图2。由于上函数与下函数类似,同上也可以得到相似的结果如图3所示。

图1 不同r值对应的模糊近似解

图2 不同r和y值对应的模糊近似上解
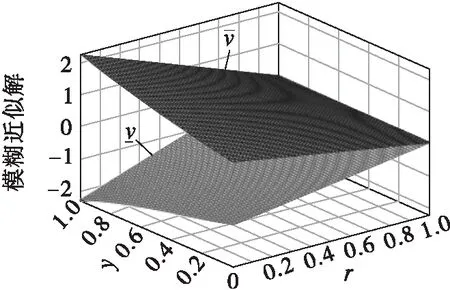
图3 不同r和y值对应的模糊近似上下解
4 总结
本文研究了在Caputo导数下的模糊分数阶积分微分方程,利用模糊Laplace变换和改进的Adomian分解方法确定给定问题的近似解。为了更好地理解改进的Adomian分解方法,本文利用数值例子来理解改进的Adomian分解方法及其在工作中的实现。为了检验近似解的确定性,用计算机算法在不同的不确定性点上绘制了与每个数值例子对应的二维和三维图。

