基于改进Wallis滤波器算法的无人机影像匀光匀色方法

杨海成 李茂森 伦更永 李云涛 梁四幺

(1. 核工业航测遥感中心, 河北 石家庄 050000;2. 中核三维地理信息工程技术研究中心, 河北 石家庄 050000)

0 引言

无人机影像生成数字正射影像主要包括3个步骤:影像几何纠正、影像色彩一致性处理和影像镶嵌。由于无人机摄影受不同拍摄环境(如太阳高度角、云雾等)、地形起伏(如高山、平地等)、相机自身特性(如曝光、白平衡等)、航摄比例尺等因素的影响,使得拍摄的影像之间和影像内部容易出现色彩不均匀、明暗不一致等问题[1]。如果这些差异不进行处理,镶嵌影像就会有明显的色彩和亮度差异,影响最终数字正射影像的色彩质量和用户的目视判读,还会给后续影像处理工作带来相应的困难[2]。无人机影像间匀光匀色是为了解决影像间亮度和色彩差异问题,按照处理思想主要分为3类:基于直方图的匀光匀色算法,基于统计方法的匀光匀色算法和基于全局的匀光匀色算法[3]。

基于直方图的匀光匀色算法[4]实质是校正影像的直方图分布,将源影像和模板影像直方图进行均衡化处理,再将均衡化影像按照映射关系进行校正。文献[5]指出直方图匹配算法虽然能直接修改影像直方图的分布形状,但是当两幅影像差异较大时,直方图匹配结果会出现偏色现象。

基于统计方法的匀光匀色算法实质是一种数学变换,先统计源影像和模板影像的相关参数,再通过数学变换把源影像的参数校正为模板影像的参数。文献[6]提出了基于Wallis滤波器的算法,将模板影像的均值和方差作为标准,通过变换源影像的灰度值,使其均值和方差与参考图像均值和方差近似,从而实现影像的匀光匀色处理。但是线性传递会出现累积误差,在纯色区域容易出现不均匀的斑点。文献[7]基于重叠区域的Wallis匀色方法,将相邻影像重叠区域内的均值和方差进行Wallis变换,当重叠区域色差较大或重叠度数较大时,影像间的色彩差异无法彻底消除。文献[8]采用分段直方图表示影像的颜色分布,将源影像局部特征结构与模板影像进行特征匹配,该方法能处理大尺度影像的色彩校正。

基于全局的匀光匀色算法一般以影像在相同地理位置有相同颜色为先验证知识,在整个测区内利用最小二乘平差使得全局色彩差异最小。为了更准确地实现色彩映射,文献[9]提出了一种新的方法,独立校正每个像素的颜色,通过颜色特征对应求解最小二乘概率移动,直接得到每个像素的独立仿射模型,但是该方法不能保证匹配特征的数量和分布合理性。文献[10]在梯度感知分解的基础上,分别进行颜色映射和细节增强,该方法很好地保留了纹理和细节。按照相同的策略,文献[11]利用梯度增强技术,开发了一种更完整和更复杂的算法来抑制细节损失,但是该方法保留的结构与原始结构在幅度上可能出现不一致。文献[12]提出多视色彩校正算法,同时考虑了单张影像的质量以及全局影像的色彩一致性,在重叠区域建立影像间颜色差异、梯度保护、对比度优化为目标方程的能量函数,求解得到颜色校正模型,通过二次样条的插值得到每个像素的颜色值,该方法校正模型比较复杂,计算量大。

以上色彩一致性处理算法在传统航空影像色彩处理中已经取得了较好的效果,但在无人机影像色彩处理过程中有一定的局限性,与传统航空摄影测量相比,无人机摄影测量的飞行高度更低,影像重叠度更大,获得的影像具有张数多、数据量大、分辨率较高等特点。而且由于雾霾或建筑物的遮挡易在局部区域形成暗区、由于镜面反射物体的强曝光易在水面形成亮斑,这让无人机影像在进行色彩一致性处理时变得更加复杂和困难[13]。为了解决无人机航摄影像色彩差异问题,本文提出了一种基于乘性系数和无人机影像像元信息的变换参数改进方法,此方法的改进在尽可能保持待匀色影像色彩损失小的条件下,使得影像间整体色调和影像内亮度均值反差一致,具有良好的匀光匀色效果。

1 传统的Wallis滤波器匀光匀色方法

Wallis滤波器实质上是一种影像增强的滤波算法,将局部影像进行变换,通过保证影像内部不同位置、不同影像之间的灰度均值和标准差近似相等来实现影像的匀光匀色处理[14]。同时,它也是一种特殊的线性变换,线性数学模型表达式为式(1)。

(1)

式中,g(x,y)表示原始影像的灰度值;f(x,y)表示结果影像的灰度值;r1表示乘性系数;r0表示加性系数,见式(2)和式(3)。

式中,sg表示原始影像的标准差;sf表示模板影像的标准差,c∈[0,1];b表示标准差系数,b∈[0,1];mg表示原始影像的灰度均值,mf表示模板影像的灰度均值。

Wallis变换的目的是将结果影像的均值和标准差强制变换到模板影像的均值和标准差,Wallis变换的一般表达式为式(4)。

(4)

式中,g(x,y)表示原始影像的灰度值;f(x,y)表示结果影像的灰度值;mg表示原始影像的灰度均值;sg表示原始影像的标准差;sf表示模板影像的标准差,c∈[0,1];b表示标准差系数,b∈[0,1];mf表示模板影像的灰度均值。

典型的Wallis滤波器中取b=1、c=1,此时式(4)变为式(5)。

(5)

式中,g(x,y)表示原始影像的灰度值；f(x,y)表示结果影像的灰度值；mg表示原始影像的灰度均值；sg表示原始影像的标准差；sf表示模板影像的标准差；mf表示模板影像的灰度均值。

2 改进的Wallis滤波器匀光匀色方法

2.1 基于乘性系数的改进

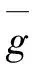
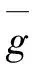
2.2 基于像元信息的变换参数改进

待处理影像块每个像元的变换参数由像元的周围信息来确定。通过以像元点为中心按照一定尺寸设定不同层级的局部区域,求取各区域均值与方差,并根据各层级分块中心像元到待处理像元的欧式距离赋予反距离权重,根据权重大小对各层级分块的均值与方差进行加权求和获取最终的变换参数,局部区域的形状通常选为正方形,如图1所示。每个小方格作为一个像元,L为指定局部尺寸。

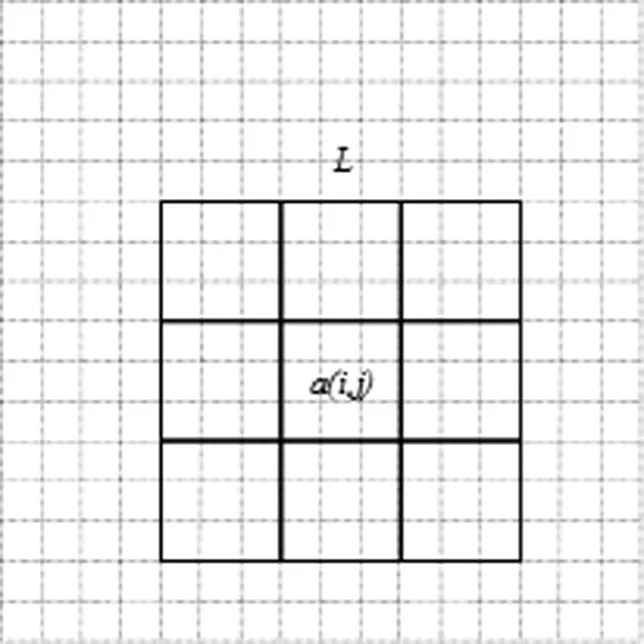
图1 影像块局部参数示意图

该像元点变换参数由自己所在方块以及周围次级分块共同决定,公式如式(8)和式(9)所示。

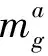
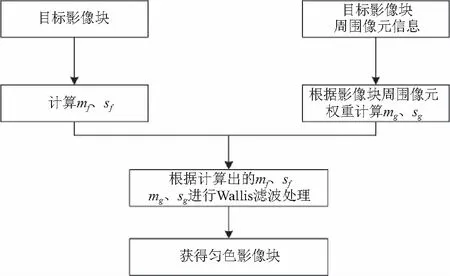
图2 基于像元信息的变换参数改进流程图

3 实验及分析

3.1 匀光匀色实验

本文使用了两组不同地形的数据分别进行实验:安徽测区对应平原地形、湖北测区对应山地地形。依次对两个测区进行Wallis滤波器实验本文改进的Wallis滤波器方法对比实验。对同一组数据从整体和局部细节采用主观视觉进行定性评价和客观指标进行定量分析,得出实验结论。实验数据如下:

(1)安徽测区。该地区气候温和,四季分明,光照充足,但是由于太阳高度角的影响,使得拍摄的像片光照不同,影响了影像的质量。由无人机影像经几何纠正和影像镶嵌后的正射影像如图3所示。经无人机影像经几何纠正、影像匀光匀色和影像镶嵌后的整体正射影像和局部放大效果如图4所示。

(2)湖北测区。该地区四季分明,冬冷夏热,雨热同季,但是由于地形起伏较大,拍摄的像片出现亮区和暗区,且有些区域影像模糊,整体来说影像的质量不佳。由无人机影像经几何纠正和影像镶嵌后的正射影像如图5所示。经无人机影像经几何纠正、影像匀光匀色和影像镶嵌后的整体正射影像和局部放大效果如图6所示。

图3 无人机源影像直接镶嵌结果

(a)Wallis滤波器整体

(b)本文方法整体

(c)Wallis滤波器局部

(d)本文方法局部

图5 无人机源影像直接镶嵌结果

(a)Wallis滤波器整体

(b)本文方法整体

(c)Wallis滤波器局部

(d)本文方法局部

3.2 主观视觉评价

安徽测区从视觉评价而言,图4(a)中Wallis滤波器实验结果:整体色调变暗,对比度下降,影像出现斑点,地物出现偏色现象,影像清晰度降低,匀光匀色效果不好;图4(b)本文实验结果影像色彩一致性,对比分明,细节清晰,目视效果良好,虽然在水面存在细微拼接的痕迹,但是总体来说,本文匀光匀色实验结果良好。

湖北某测区从视觉评价而言,图6(a)中Wallis滤波器实验结果:整体色彩一致性较好,但与源影像的色调发生了较大变化,影像出现偏色,细节模糊,影像清晰度降低,匀光匀色效果较差;图6(b)本文实验结果:影像色彩一致性好,镶嵌线处的色彩差异较小,目视效果良好。

3.3 客观数据分析

客观指标评价是通过计算能够反映结果影像色彩质量的参数指标,再进行定量分析参数值的一种方法。本文采用的客观指标评价参数[15]有:均值、标准差、平均梯度、信息熵等。

3.3.1安徽测区客观指标评价参数

如表1和表2所示,安徽某测区从客观指标评价而言,本文算法均值与源影像的均值最接近,说明色彩保持较好;本文算法信息熵最大,说明影像信息丰富;本文算法平均梯度分别最高和次高,说明细节保持良好,影像清晰;本文算法的标准偏差为次小,说明影像灰度分布比较集中,像素之间差异较小。总体来说,本文算法在客观指标评价中具有优势。

3.3.2湖北测区客观指标评价参数

如表3和表4所示,湖北某测区从客观指标评价而言,由于测区内明暗差异较大,本文实验均值与源影像的均值差异较大,但是与其他方式而言是最接近和次接近源影像均值的,说明色彩虽有调整,但是保持较好。本文方法信息熵最大,说明进行色彩调整时保持了影像的信息。本文方法平均梯度分别为最高和次高,保持了影像的细节,明暗一致,消除了条带现象。总体而言,湖北测区实验结果表明本文算法的校正效果最佳。

表1 安徽测区整体匀光匀色实验结果客观指标参数

表2 安徽测区局部匀光匀色实验结果客观指标参数

表3 湖北测区整体匀光匀色实验结果客观指标参数

表4 湖北测区局部匀光匀色实验结果客观指标参数

4结束语

(1)针对传统Wallis滤波器匀光匀色算法不能解决无人机影像内部存在的亮度不均、反差不一致等现象,影响无人机影像匀色效果。本文提出了一种基于乘性系数和无人机影像像元信息的变换参数改进方法,此方法的改进在尽可能保持待匀色影像色彩损失小的条件下,使得影像间整体色调和影像内亮度均值反差一致,具有良好的匀光匀色效果。

(2)通过对实验数据分别进行Wallis滤波器和本文改进方法实验结果的主观视觉和客观数据评价分析证明,在传统的Wallis滤波器算法上对乘性系数和像元信息的变换参数的改进,验证了在无人机影像匀光匀色处理效果上的显著优势,具有一定的推广应用价值。