基于EMD方法的组合预测模型在建筑物基坑沉降监测中的应用

杜建广 沈 尤 常旭辉

(中国电建集团北京勘测设计研究院有限公司, 北京 100024)

0 引言

近年来,我国高层建筑物数量快速增长,在影响高层建筑物安全建设的众多因素中,基坑的沉降最为严重。建筑物基坑沉降不仅会造成基坑的变形与坍塌,还会对基坑保护区内其他建构筑物的安全造成影响。为了保障建筑物施工过程中基坑本身及周围建构筑物的安全,基坑的沉降监测尤为重要,能够对基坑是否发生变形提供数据支撑,为了准确评估建筑物基坑的变形趋势,控制变形量,基于基坑当前监测数据对未来一段时间内的变形量进行预测可以有效对基坑的安全性进行评估。

目前常用的变形预测模型有时间序列分析模型、反向传播(back propagation,BP)神经网络模型、灰色系统分析模型等[1]。相比于其他预测模型,灰色系统GM(1.1)模型的优势在于基于规律性与样本量都较小的原始数据就可进行变形预测,有着较强的规律性搜索能力,解决了“小样本、贫信息”的变形预测问题[2]。BP神经网络模型是一种智能化预测模型,通过自适应学习与计算可以对非线性信号进行较为准确的预测[3]。结合上述两种预测模型的优势,不少学者进行了研究,文献[4]有效结合灰色理论有BP神经网络模型,将组合模型应用于实际变形监测项目中,得到的预测精度较高;文献[5]将遗传算法添加至灰色神经网络中,实现全局最优求取的效果。然而,上述算法没有考虑到非平稳时间序列中的趋势项,直接将灰色预测残差作为BP神经网络输入项会导致模型预测精度的受损。

本文在灰色神经网络模型的基础上,提出了一种改进型组合模型。该组合模型通过经验模态分解(empirical mode decomposition,EMD)方法实现信号的自适应分解,得到不同频段分量,对于稳定性较高的低频分量使用差分灰色神经网络模型进行预测,提高了灰色预测残差的稳定性,相比于灰色神经网络模型的预测精度更高;针对稳定性较差的高频分量,使用自相关性强的AR时间序列预测模型进行预测。将本文提出的组合模型应用到某在建建筑物基坑沉降监测数据预测中,并将预测结果与传统预测模型预测结果进行对比。

1 EMD分解与重构

EMD方法对信号进行处理的思想是:任何信号都是由一些频率不同的本征模态函数(intrinsic mode function,IMF)组成[6],IMF分量满足条件为：①上下包络线均值为零,也就是上下包络线关于时间轴对称;②过零点个数与极值点个数相差在一个以内。信号的时频特征通常由相邻极值点的间隔进行反映，如果信号不存在极值点,可对信号进行多次求导获得极值点。

使用EMD方法对高层建筑物基坑变形数据进行预处理,获取不同频率的IMF分量,得到理想分辨率下的低频分量与高频分量。针对高频分量,由于其具有较强的自相关性,采用自回归模型(autoregressive model,AR)进行预测;针对低频分量,采用差分灰色神经网络模型进行预测。

2 差分灰色神经网络模型

作为对灰色神经网络的一种改进,差分灰色神经网络模型实现变形数据的预测与分析的原理为:对经灰色预测得到残差进行差分化处理,将差分化处理得到的平稳序列输入至BP神经网络中,利用神经网络的自适应学习预测变形数据。

2.1 GM(1.1)模型

假设有一时间序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)},x(0)(n)表示第n期观测值。通过GM(1.1)模型实现时间序列预测的步骤为[7]:

(1)通过对原始观测数据进行累加:X(1)={x(1)(1),x(1)(2),…,x(1)(n)}。

(2)紧邻均值生成序列:z(1)(k)=1/2(x(1)(k)+x(1)(k-1)),k=2,3,…,n,得到新数列z(1)={z(1)(2),z(1)(3),…,z(1)(n)}。

(3)通过对新序列构建白化方程,得到式(1)。

(1)

式中,b表示灰色作用量;a表示发展系数,a可通过最小二乘原理求解得到,其中a=[ab]T=(BB)-1BTY,B与Y可表示为式(2)。

(2)

求解白化方程,得到式(3)。

(3)

通过累减对原序列进行还原,得到:¯x(0)(k+1)=¯x(1)(k+1)-x(1)(k),同时得到预测值x(0)(n)。

2.2 灰色预测的残差差分化

将灰色模型预测残差作为BP神经网络的输入数据可能会造成网络无法收敛。因此,需要对GM(1.1)模型预测得到的残差进行差分处理,避免因残差序列的不平稳造成的模型收敛速度慢以及预测精度降低。

将GM(1.1)模型预测得到的残差序列记为e(0),对e(0)进行差分处理,得到一阶差分项e(1)，见式(4)。

(4)

将平稳化残差序列e(1)(t)输入至BP神经网络中进行训练。

2.3 BP神经网络模型

BP是一种多层前馈神经网络,信息向前传播、误差逆向传递。使用BP神经网络进行数据预测不需要事先将输入与输出的映射关系进行确认,而是通过纯机器学习的方法,在算法中输入集,算法自动对输入集学习、训练,从而得到某种特定的规则[8]。

对网络进行训练的具体步骤为[9]:

(1)网络初始化。根据输入序列X与输出序列Y对输入层节点n、隐含层节点l与输出层节点m进行确定,初始化输入层与隐含层神经元间的连接权值wij以及隐含层与输出层神经元间的连接权值wjk,同时还要初始化的参数有神经元激励函数、给定学习速率lr以及隐含层阈值与输出层阈值a1、a2。

(2)隐含层输出计算。通过隐含层阈值a1与输入层、隐含层神经元间的连接权值wij对隐含层输出进行确定，见式(5)。

(5)

式中,Hj表示隐含层输出;f表示隐含层激励函数,本文选择sigmoid作为隐含层激励函数，见式(6)。

(6)

(3)输出层输出计算。通过输出层阈值a2、隐含层与输出层神经元间的连接权值wjk以及隐含层输出Hj对预测输出进行确定，见式(7)。

(7)

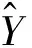
(4)误差计算。通过期望输出与预测输出计算得到预测误差ek，见式(8)。

(8)

式中,Y表示期望输出值。

(5)权值更新。使用预测误差ek对各层之间的权值wij与wjk进行反向更新。

(6)阈值更新。使用预测误差ek对节点阈值a1、a2进行反向更新,见式(9)。

(9)

(7)迭代是否结束判断。若迭代结束,将预测值输出,若没有结束,重复上述步骤。

3 AR自回归模型

在构建自回归模型前首先计算时间序列的自相关系数。假设有一时间序列X,该时间序列的相关系数为r1,r2,…,rn。t时刻观测值为xt,t+k时刻观测值为xt+k,二者之间的自相关系数rk表示为[10]式(10)。

(10)

式中,¯x表示时间序列X均值。

AR模型能够得到广泛使用的原因在于在建模时不需要涉及白噪声序列解算,只要对线性方程组进行求解即可，见式(11)。

(11)

式中,φ1,φ2,…,φp表示自回归系数;p表示阶数;εt表示与xt不相关的白噪声序列。

4 基于EMD的组合预测模型

综合上述算法的优势,本文提出了一种基于EMD的差分灰色神经网络-AR模型,该组合预测模型的具体算法为:

(1)将建筑物基坑沉降监测数据进行EMD自适应分解,得到一系列不同频率的IMF分量,其中c1表示低频分量,d1、d2、d3表示高频分量。

(2)对于低频分量c1,使用本文提出的差分灰色神经网络进行预测,得到拟合值与预测值y。

(3)对于高频分量d1、d2,使用AR模型进行预测,分别得到拟合值与预测值y1、y2。

(4)对于高频分量d3,将其视为噪声项予以剔除。

(5)综上可以,建筑物基坑变形监测数据X可表示为X=c1+d1+d2+d3,c1、d1、d2的预测值分别为y,y1、y2,将各自预测值进行累加即可得到建筑物基坑沉降预测值Y=y+y1+y2。

图1为本文提出算法的技术路线。

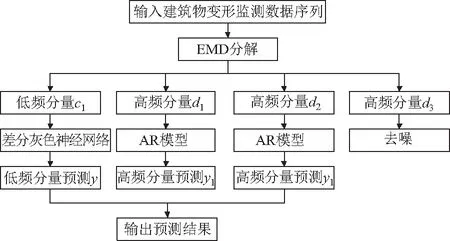
图1 本文提出算法的技术路线

5 实例分析

5.1 工程概况

本文以北京市朝阳区某在建居民楼项目的基坑沉降监测数据为例进行算法的验证,该基坑深度约6 m。为保障项目在建设过程中的安全,经实地踏勘,按照三级基坑控制的思想布设7个监测点,分别为J1～J7。使用二等水准按闭合路线,结合成本与效率的考虑对7个监测点实施复测。

5.2 变形预测与分析

选取该基坑监测点J4点连续40期累计沉降监测数据为例进行变形预测,其中前30期监测数据用于建模,后10期监测数据作为预测数据期望值,对模型预测的效果进行检验。

使用EMD分解前30期监测数据序列。使用差分灰色神经网络对低频分量c1进行预测,其中参数设置为:输入层、隐含层、输出层神经元个数分别为4、9、1,分别选择tan sig、purelin作为隐含层与输出层的神经元传递函数。选择最大最小值法对训练样本进行归一化处理,以避免训练结果受数据本身影响。

本文通过计算排列熵(permutation entropy,PE)区分高频分量与低频分量,排列熵是一种对时间序列随机性程度进行检测的方法,信号的复杂程度越高,排列熵值就会越大；反之,排列熵值越小。多尺度排列熵(multi-scale permutation entropy,MPE)是对排列熵方法的一种改进,它能够更加准确地对信号的随机性进行分析。多尺度排列熵的基本思想是对时间序列的多尺度粗粒化,将多尺度阈值熵的阈值设置为0.6,也就是说,多尺度排列熵的值大于0.6的分量为高频分量,多尺度排列熵的值小于0.6的分量为低频分量。

计算经EMD分解沉降监测数据得到的IMF分量的MPE值,区分出高频IMF分量与低频IMF分量,各分量的MPE值如表1所示。

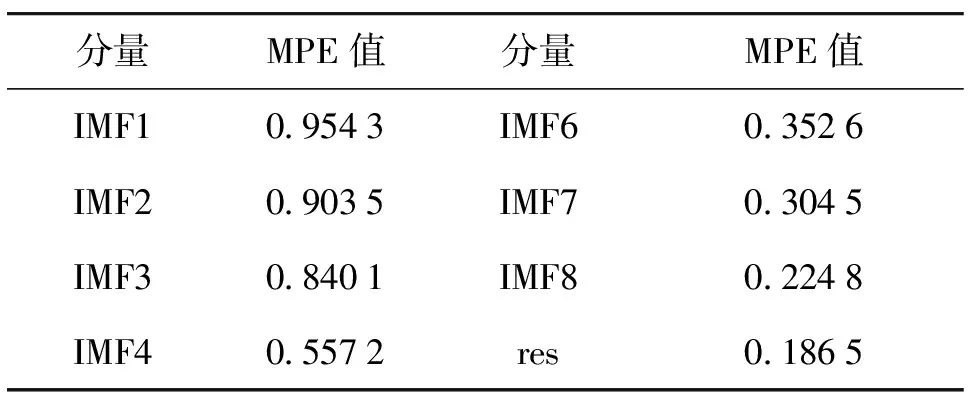
表1 各IMF分量多尺度排列熵

从表1中可以看到,前3个IMF分量的MPE值均大于0.6,故可将前3个IMF分量定为高频分量。通过频谱计算得知,第1个IMF分量主频位于0.25～0.5 Hz频段,振幅小于1 mm,呈现噪声特征,可将前第1个IMF分量认定为高频噪声分量,予以剔除;第2、第3个IMF分量的主频位于0.1～0.25 Hz频段,可认为此频段反映了建筑物基坑的沉降特性,将第2、第3个IMF分量认定为高频分量d1、d2;将剩余分量认定为低频分量c1。

使用AR预测模型对高频分量d1、d2进行建模,使用PACF定阶段法确定d1、d2分量均为2阶。

使用差分灰色神经网络对低频分量进行预测得到结果如图2所示;使用AR模型对高频分量进行预测得到结果如图3所示,同时给出了预测结果误差百分比。

对上述各分量预测结果进行重构,最终得到建筑物基坑沉降拟合值与预测值。将GM(1.1)模型、灰色神经网络模型与本文提出预测模型预测结果进行对比,如表2所示为利用3种预测模型对建筑物基坑J4点第31～40期沉降预测结果。

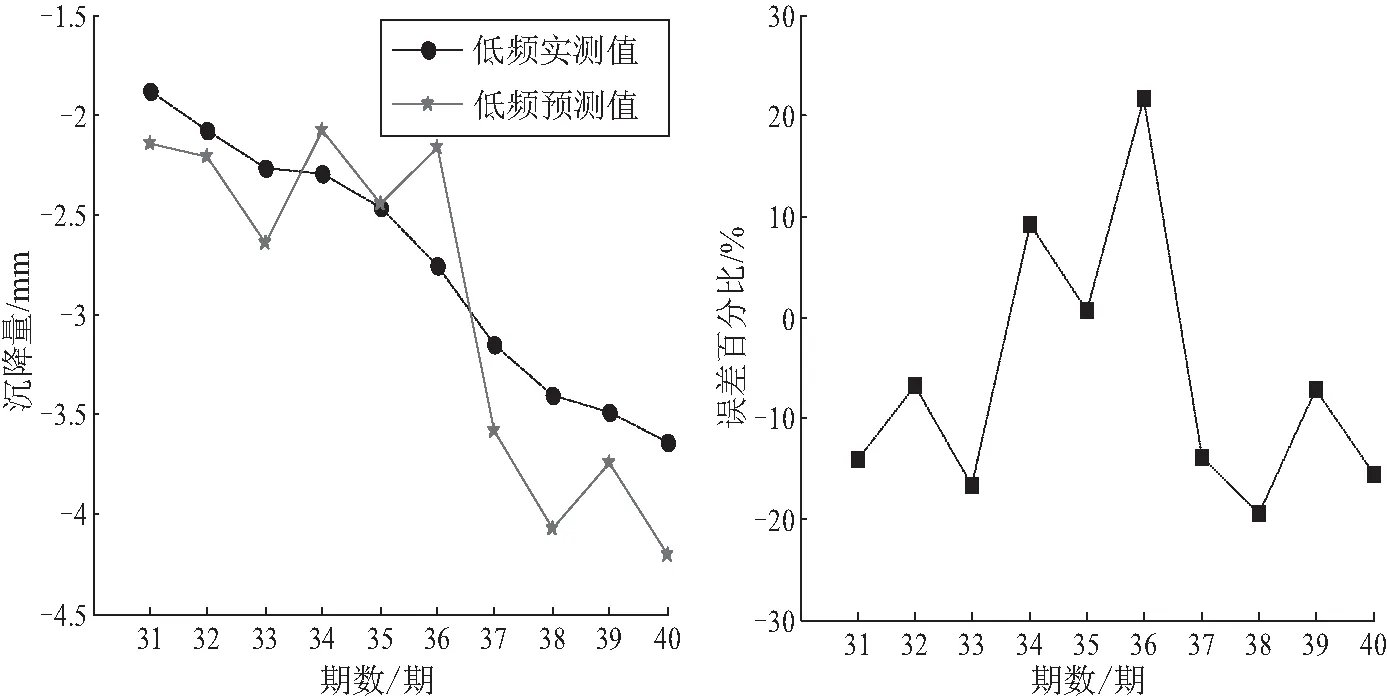
图2 低频分量预测结果

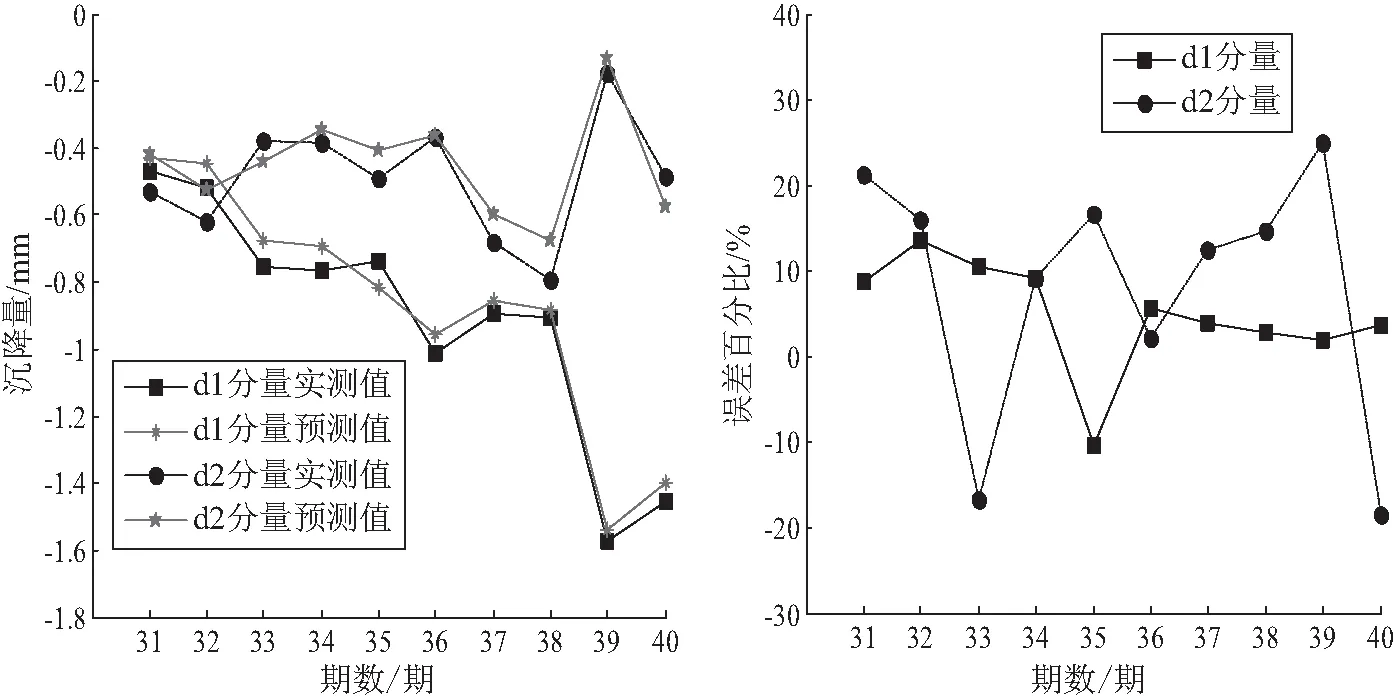
图3 高频分量预测结果

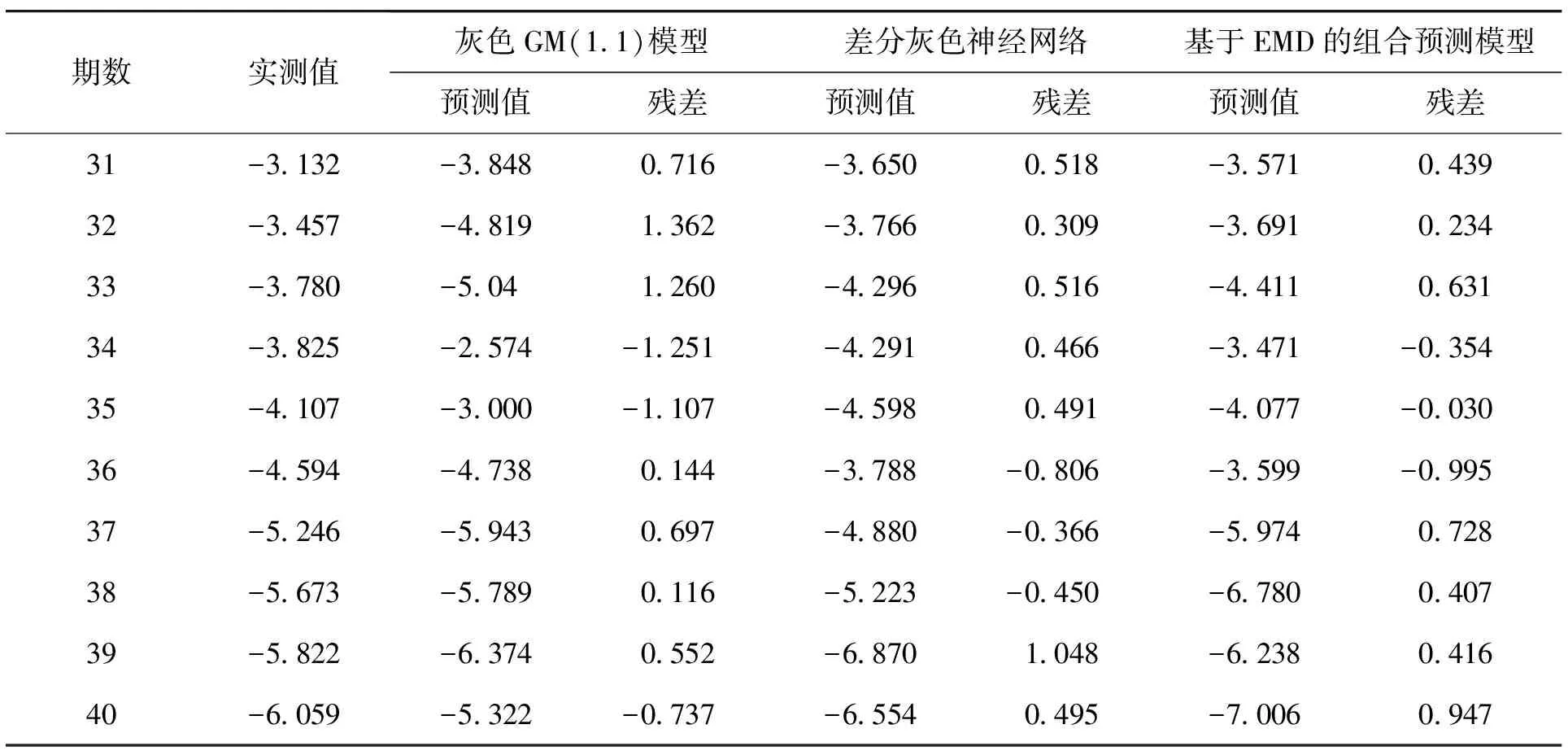
表2 3种模型预测结果单位:mm

通过表2计算可知,利用GM(1.1)模型进行建筑物基坑沉降监测数据预测结果的残差平均绝对值为0.794 mm;利用差分灰色神经网络进行建筑物基坑沉降监测数据预测结果的残差平均绝对值为0.547 mm;利用本文提出的基于EMD的组合预测模型进行建筑物基坑沉降监测数据预测结果的残差平均绝对值为0.518 mm。相比于前两种预测模型,本文提出的预测模型预测效果更好,验证了本文算法的可靠性与优越性。传统变形预测模型仅考虑单因子变化,不适用于具有非线性、非稳定性特征的建筑物基坑变形预测的情况。充分考虑建筑物基坑非线性、非稳定性的变形特征,提出了基于EMD的组合预测模型并应用到建筑物基坑变形监测中,通过差分灰色神经网络模型消除了由于灰色预测残差不平稳而导致的预测误差,同时发挥了AR时间序列模型自相关强的优势[12-15]。

6 结束语

针对传统时间序列预测模型在针对非平稳序列预测中的劣势,本文结合多种预测模型优势,提出了一种基于EMD方法的改进预测模型。该预测模型有效消除了灰色预测残差不稳定的问题,通过EMD方法对基坑沉降监测数据进行分解,得到不同频段的IMF分量。针对低频段稳定性更好的序列,使用差分神经网络模型进行预测;针对高频段不稳定的序列,使用AR模型进行预测,充分利用了AR模型自相关强的优势。将不同频段分量经预测模型预测得到的序列进行重构得到最终预测结果。

将灰色GM(1.1)模型、差分灰色神经网络模型与本文提出组合模型应用于北京市朝阳区某在建小区建筑物基坑沉降监测数据预测中,通过对比3种模型预测结果,得到改进后的模型预测精度更高,能够会建筑物基坑沉降的变形趋势做出更加准确的预报。