基于蚁群优化支持向量机的电力人因事故预测模型*

王 鹏 董建房

（陆军炮兵防空兵学院基础部 合肥 230031）

1 引言

近年来，随着科技的快速发展，社会的不断进步，各行各业对电力供给的要求不断提高，但是电力人员死亡事故、大规模停电事件还是不时发生，这引起了政府和公众的注意，特别是电力人员伤亡事件更是每年在各地都有发生，极大地影响了电力的供给，而在这些电力人员伤亡事故中人因又占了90%［1］，因此对电力行业的生产安全现状进行评估和预测成为了一件刻不容缓的工作，对电力安全的评估和预测可以为改良电力行业生产模式，减少电力安全事故发生数量，提高电力生产行业安全性提供有效参考。目前国内外对人因事故［2～3］评估模型主要有层次分析法［4］、模糊综合评判法［5］、贝叶斯网络［6～7］等，但是这些评估方法具有太多主观因素，而支持向量机［8～10］是一种建立在统计学习理论基础上的学习方法，SVM 的原则是实现结构风险最小化，因此SVM 在小样本、非线性问题中表现突出，而电力人因事故每年的发生次数并不是很多，但是每次发生都影响广泛，造成极严重的后果，而利用一般的方法如线性规划等对电力人因事故进行预测效果并不理想，但是支持向量机完美契合了电力人事故的特点，因此选用支持向量机对电力人因事故进行预测比较合适。所以，为对电力行业安全生产情况进行预测，本文基于蚁群算法优化的支持向量机建立了电力人因事故数量预测模型，并且根据全国2009 年～2018 年10 年内的电力人因事故数据，进行评估和预测，达到了较好的预测精度。

2 电力人因事故数据统计模型

2.1 支持向量机原理

支持向量机［11］的工作目标是最大化不同类别之间的间隔，使得支持向量机的分类具有更高的可信度和泛化能力。支持向量是指在支持向量机分类过程中那些靠近边界的数据点。支持向量机的目标是寻找一个最优超平面，这个最优超平面能够正确地分割正类和负类样本。最优超平面ωT x+b=0 可通过做一个非线性映射得到。当样本集线性可分时，寻优问题为

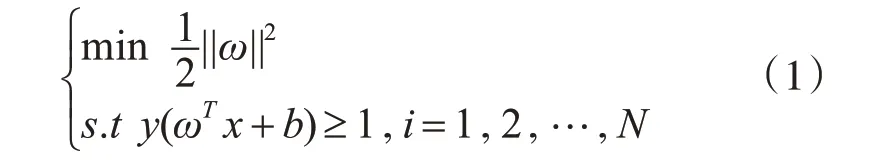
当样本集线性不可分时，加入松弛变量ξi＞0和惩罚因子C，它代表了对离群点的容忍程度，因此，式（1）成为凸二次规划问题：

为解决线性不可分问题，通常方法是寻找核函数［12～13］。将一个低维的样本集向高维空间做映射，在这个过程中找到的一种函数，它能够使得样本集在低维空间与高维空间的内积结果一致，这种函数称为核函数。常用的核函数有高斯径向基核函数、多项式核函数等。

引入核函数k(xi,xj)和拉格朗日乘子αi，可以将式（2）变为如下形式：

本文选用应用较为广泛的径向基核函数，其表达式为

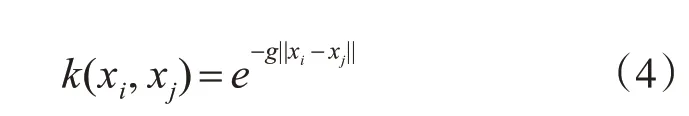
其中g为核参数，代表了径向基核函数作用的宽度，C为惩罚因子，因此，为使得本文的电力人因事故数量预测模型更加精确，必须要选择合适的参数。

2.2 基于蚁群算法的支持向量机优化模型

蚁群算法是一种主要用于寻找最优路径的算法，作为一种仿生算法，它主要运用了正反馈和分布式计算的特征进行搜索［14］，是一种贪婪式启发式的优化算法。利用上述特点，本文利用蚁群算法［15～16］来选择合适的参数，优化参数的选择过程，建立精度更高的的电力人因事故数量预测模型。结合传统的支持向量机和蚁群算法，建立基于改进支持向量机的电力人因事故预测回归模型，目标函数为

其中l为样本的数量；yi为实际值；f(xi)为预测值。

蚁群算法的具体搜索方法如下：1）初始化相关参数；2）生成节点及路径；3）迭代搜索；4）终止。

3 电力人因事故预测

3.1 基于CAC-SVM的电力人因事故预测

以我国2009 年～2018 年电力人因事故死亡人数为例，运用改进的支持向量机进行电力人因事故死亡人数预测，使用Matlab 软件进行运算，过程如下。

步骤一：数据归一化。为更加方便地进行对比和运算，利用本文的模型得到更加精准的预测结果，对统计得到的数据进行归一化，可得到处理结果如表1所示。

表1 事故死亡人数归一化

步骤二：利用蚁群算法优化参数选择路径。利用蚁群算法对本文的支持向量机预测模型进行参数优化，首先初始化相关参数：c取值为（0.01，200），ε取值为（0，0.8），σ取值为（0.001，100）；m=50 ，Nmax=500 ，ρ=0.7 ，α=1 ，β=5 ，Q=100。利用计算软件Matlab 进行计算，可得到最优训练参数。

步骤三：将上一步骤中得到的最优参数代入回归方程，可以得到电力人因事故死亡人数预测结果如表2。

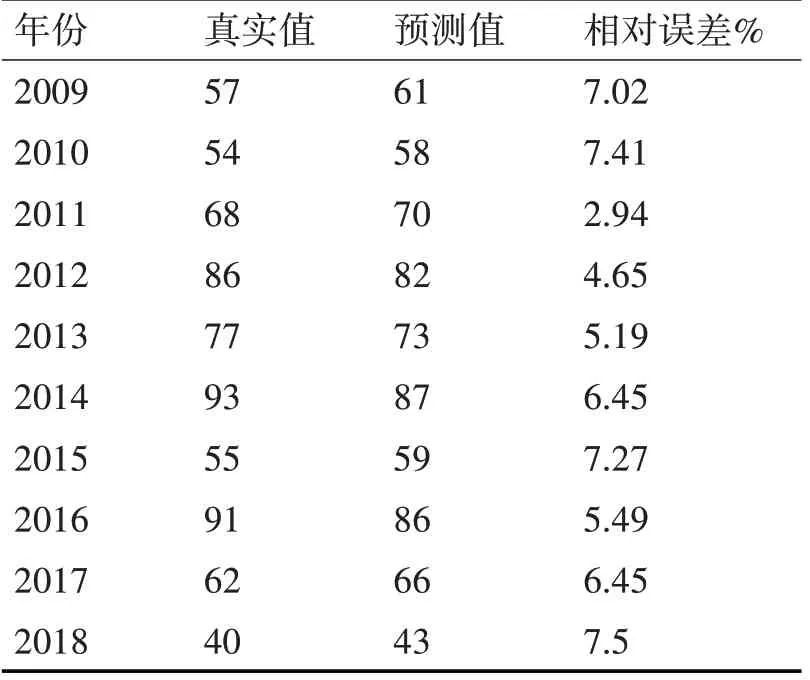
表2 ACA-SVM预测结果

3.2 预测模型的有效性

为了确定本文提出的基于优化支持向量机的电力人因事故预测模型的正确性，本文利用传统的支持向量机方法对同样的数据样本进行回归计算，得到了预测结果。为更加直观地对比两种预测结果，本文使用相对误差来判断两种方法的预测精度。对于从传统支持向量机模型，选择最优参数后，代入模型，可得到预测结果如表3所示。

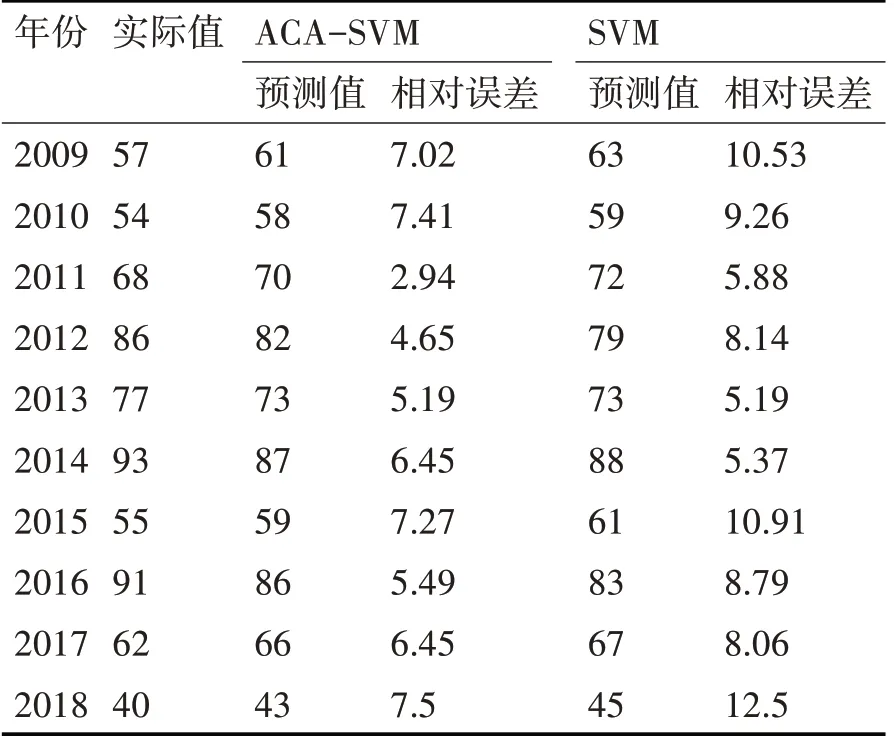
表3 ACA-SVM与SVM对比结果

为方便进行对比分析，将人因事故的实际值、ACA-AVM 的预测值、SVM 的预测值做成对比图，如图1 所示。图2 为ACA-AVM、SVM 的两种方法进行预测的相对误差。

图1 预测值对比

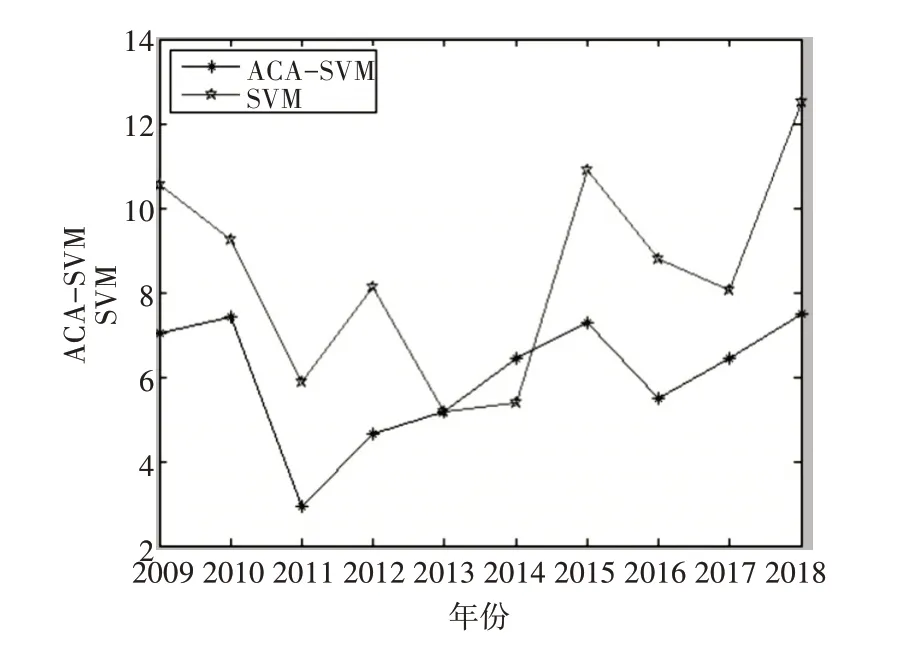
图2 相对误差对比

由表对比可知，使用蚁群算法优化的支持向量机对电力人因事故预测精度比单纯使用支持向量机高，这说明使用蚁群算法优化的支持向量机可以较为准确地预测近年的电力人因事故数，从而为电力行业的发展提供一定的依据。

在对比完成后，利用蚁群算法优化的支持向量机对2019 年、2020 年的电力安全人因事故数量进行预测，得到结果为67、84，虽然因为电力人因事故为小样本的原因，可能预测精度不是很高，也可能会发生很大的误差，但是根据上文实验的相对误差情况分析，支持向量机的预测结果还是具有一定参考价值的。分析10 年来的电力人因事故数量，从2009 年～2018 年电力人因事故数量呈现波浪状起伏态势，2017、2018 两年电力人因事故数量很少，所以2019、2020 年事故数量上升是有一定意义的。

4 结语

1）支持向量机建立在统计学习理论基础上，在小样本、高维、非线性问题上表现突出。因此作者利用SVM 构建了电力人因事故数据统计模型，用该模型能够较为准确地预测电力人因事故次数，能够增加管理部门决策的科学性和准确性。

2）两种不同预测模型的对比结果显示，基于蚁群算法的支持向量机电力人因事故预测模型预测精度更高，误差更小，可以用来进行电力人因事故预测，在实际生产生活中具有一定的应用价值。