西安市空气质量影响因素的分位数回归分析

刘 笑

(西安财经大学 统计学院, 西安 710100)

当前各国经济的快速发展导致了环境问题越来越严重,不论是何种原因造成的空气中PM2.5的浓度增加，都应该受到关注。

近几年,西安市雾霾日益严重，人们生活以及健康受到了一定的影响。研究发现PM2.5并非是一种成分单一的空气污染物，空气中的很多成分，例如小分子污染物、可溶性的气体和固体都组成了空气中的PM2.5。另外，有一部分学者更关注于空气中PM2.5的组成，最终发现不仅仅空气中的二氧化硫、二氧化氮对PM2.5的浓度有影响，还有很多不能想象的风速、湿度等气象的因素，甚至于降水量都会对空气中PM2.5的浓度产生或多或少的影响。

大部分空气质量方面的预测都是点估计，无论是国内还是国外都鲜少有人会对空气质量整个分布的预测进行研究，而分位数回归的预测方法几乎没有被提到。在已有研究中，学者们选择建立线性分位数回归模型得出污染物排放是导致PM2.5浓度升高的最主要原因，气象因素对PM2.5浓度变化有一定影响，但其影响小于污染物排放。在不同分位点上，PM2.5浓度在不同的季节差异较大，且数据大都是2009年至2015年的，缺少近几年环境影响的变化，需要取得更新的数据进行完善分析。

由于各因素对PM2.5浓度的影响也有可能是非线性的，因此选择建立线性分位数回归模型和普通多元回归模型，检测空气污染物和气象因素对PM2.5存在的影响。由于西安市空气质量影响最严重的因素为PM2.5的浓度，因此着重研究PM2.5的构成以及成因，研究对PM2.5浓度的影响因素。

1 文献综述

近年来，很多学者对大气环境污染情况进行了一定的研究。徐衡对宝鸡市空气质量的主要污染物PM2.5、O3的影响因素以及变化规律进行了研究，得出PM2.5和O3严重污染空气质量的结论[1]；杜越首先描述了中国AQI(空气质量指数)的时空分布，然后通过贝叶斯时空模型和广义线性模型研究气象和经济因素对AQI产生的影响，得出大气污染呈现明显的时空聚集性的结论[2]；武鹏程利用数据挖掘中的遗传神经网络模型以及灰色关联度的方法对武汉市的空气质量影响因素进行了实证分析[3]；梁鑫等通过引入次要污染物，建立新的空气质量评价模型，对中国近几年主要城市的空气质量进行了评价分析[4]；张燕杰运用相关分析法和主成分回归分析法研究了空气污染物对AQI的影响程度[5]；李雪超建立了线性分位数回归模型以及半参数可加分位数回归模型，对兰州市2013—2016年的PM2.5浓度的影响因素进行了分析[6]；颜如玉于2019年建立了普通多元回归模型和分位数回归模型来预测和研究上海市空气质量及污染源的研究[7]；随后郑林昌等对河北省城市空气污染物对PM2.5浓度值的影响做出研究[8]。

从上述的这些文献中可以看出，大多数学者是从某一种空气污染物，或其中某一种外在因素入手来进行研究，得到大气污染物会对空气质量产生负向影响的结果，但很少有学者从分位数回归的角度去研究空气质量的影响因素或是研究真正影响空气质量物质的成因[9]。基于以上分析结果，本文选择建立线性分位数回归模型和普通多元回归模型，检测空气污染物对PM2.5存在的影响。

2 数据来源及模型

2.1 数据来源

所选择的数据是2017年1月到2019年12月西安市空气质量监测月数据和气象记录月数据，总共有900个数据。其中包含PM2.5浓度、SO2浓度、NO2浓度、月平均风速、月平均温度、月平均降水量。然后分别对污染物浓度指标以及各气象因素指标进行描述性统计，来分析不同季节的PM2.5浓度情况，具体结果见表1、表2。

表1 污染物浓度指标描述性统计

表2 气象指标描述性统计

2.2 模型选择

2.2.1 多元线性回归模型

在相关变量中将其他一个或多个变量视为自变量，而只有一个因变量。在实际问题中，一个变量往往受到多个变量的影响，表现在线性回归模型中的解释变量有多个，为此构建多元线性回归模型[10]。

多元线性回归模型的一般形式为

Yi=β0+β1X1i+β2X2i+…+βkXki+μi，
i=1,2,…,n

(1)

式中：k为解释变量的数目；βj(j=1,2,…,k)称为回归系数。式(1)也被称为总体回归函数的随机表达式。它的非随机表达式为

E(Y|X1i,X2i,…,Xki)=
β0+β1X1i+β2X2i+…+βkXki

(2)

式中，βj被称为偏回归系数。

在做多元线性回归模型的参数估计时选取和一元线性回归方程的参数估计是相同的，所以可以选用相同的方法进行参数估计，也是在要求误差平方和(∑e)为最小的前提下，用最小二乘法求解参数。以二线性回归模型为例，求解回归参数的标准方程组为

(3)

解此方程可求得b0、b1、b2的数值。

2.2.2 线性分位数回归模型

分位数回归相对于普通的多元回归来说更加方便,所包含的信息也更加全面,不仅仅能看出整体的分布特点，也能看出不同分位点上的变化情况。

给定τ∈(0，1)，Y/X的τ阶条件分位数为

(4)

式中，βτ为τ分位数的回归系数，可以用最小化来解决这个估计量问题，即

(5)

式中，z′i=(1,x′i)′，ρτ(u)=u{τ-I(U<0)}称为检验函数，常用单纯型算法、内点算法和平滑型算法求解。

3 实证分析

3.1 多元线性回归模型

在做多元线性回归模型时，需要了解各因素和被解释变量的相关性，确定是否能够合理构建模型。各因素的相关性具体结果见表3。

表3 Pearson相关性分析结果

由表3可知，相关系数因为是两两相关，各变量之间相关系数较高，所以可能存在多重共线性。

由表4可以看出除了月平均二氧化硫的浓度之外其他的变量均不显著。因此选择用逐步回归的方法选择自变量，具体结果见表5。

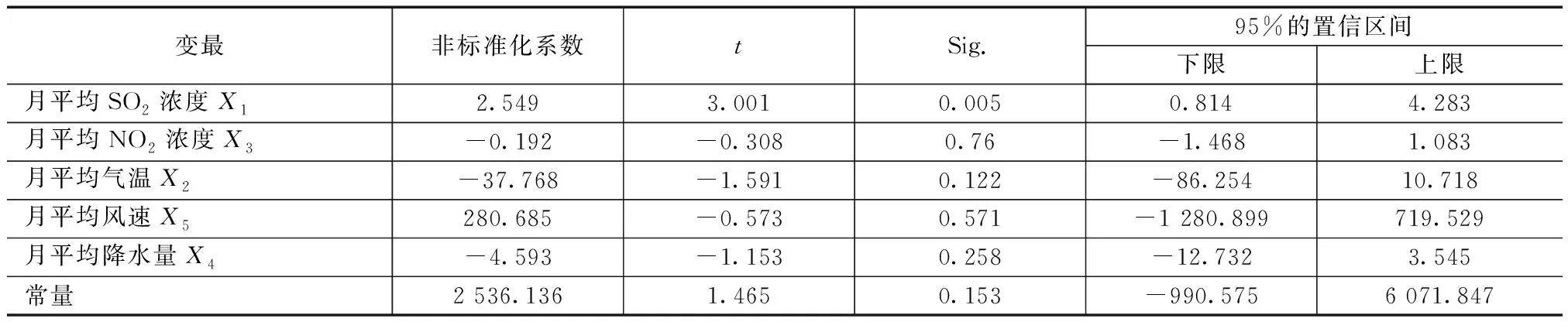
表4 各影响因素系数

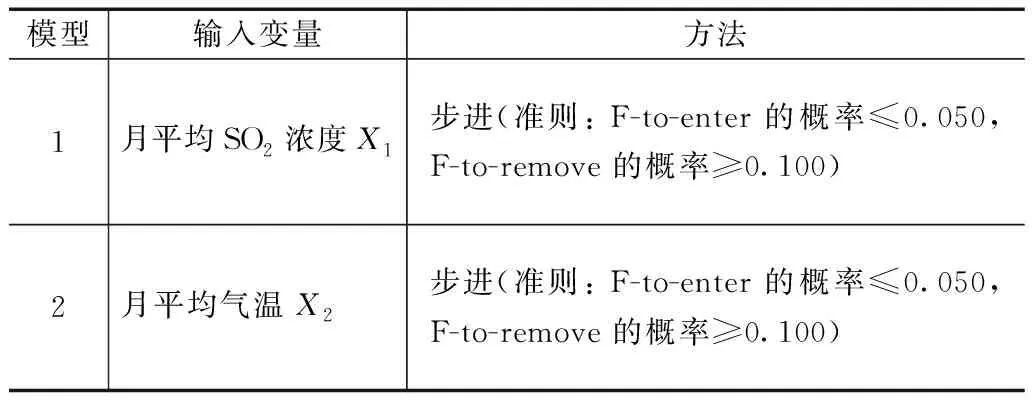
表5 逐步回归结果

由表5可以看出，最终的回归结果是月平均SO2浓度和平均气温。

为研究模型整体是否显著，需要通过方差分析来判断整体是否显著，具体结果见表6。

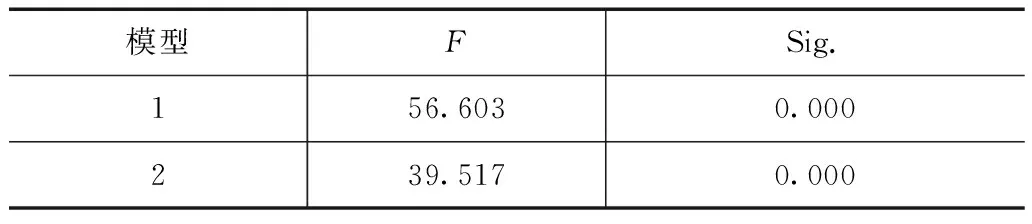
表6 方差分析结果

由表6可以看出，模型整体显著。

根据逐步回归的结果筛选出合适的变量，将所选取的变量进行残差检验，具体结果如图1所示。

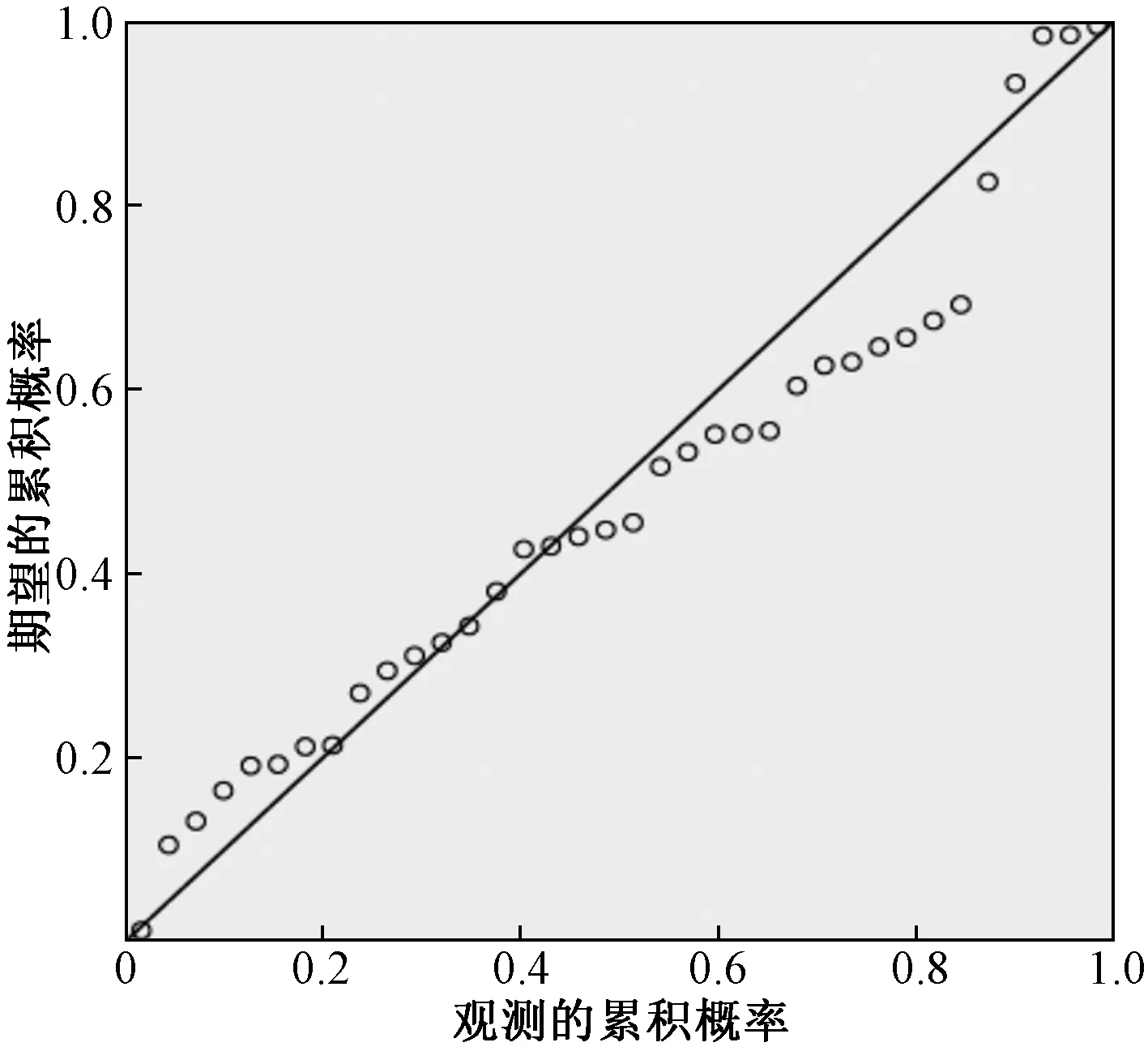
图1 回归标准化残差的标准P-P图

根据图1可知，各因素通过正态性检验,所以适合运用普通多元回归模型进行检验。因此构建普通多元回归模型。具体结果见表7。

根据表7可以得出回归方程为

Y=2.495X1-51.084X2+1 605.009

(6)

由表7可以看出，月平均SO2的浓度与月平均气温的t检验均低于0.05，说明月平均SO2浓度与月平均气温对月平均PM2.5浓度具有显著影响。

表7 各因素系数

3.2 分位数回归模型

为了解决变化趋势的问题，对所求的变量之间构建线性分位数回归模型，分析0.1、0.25、0.5、0.75、0.9分位点上5个不同变量对空气中月平均PM2.5浓度的影响。

表8为构建的线性分位数回归模型所输出的在不同的分位点上的回归系数的结果。在每一个分位点上月平均SO2浓度对PM2.5浓度是正影响。SO2系数在0.1分位点的值最大，在0.75分位点的值最小，但在0.25和0.9分位点的值基本是相差不多的，所以它所表现出来的是类似于一个二次函数分布特点的形状，具有起伏波动。

月平均NO2在0.1和0.75分位点时对PM2.5浓度是负影响。而在其余3个分位点基本都是差不多的，这说明月平均NO2浓度对月平均PM2.5浓度的影响基本为均衡状态。

月气温系数在0.25、0.5、0.75、0.9分位点时为负值且系数越来越大呈现上升趋势，说明月平均气温对月平均PM2.5浓度是负影响且随着PM2.5浓度增加，气温的影响逐渐下降。

月平均降水量在任何分位点上对月平均PM2.5浓度都是负影响。

月平均风速在0.1、0.25、0.9分位点上对月平均PM2.5浓度存在负影响，而在0.5和0.75分位点是正影响。

不同分位点上5个变量对PM2.5浓度影响存在差异。根据表8可以得到不同分位点上的回归方程。

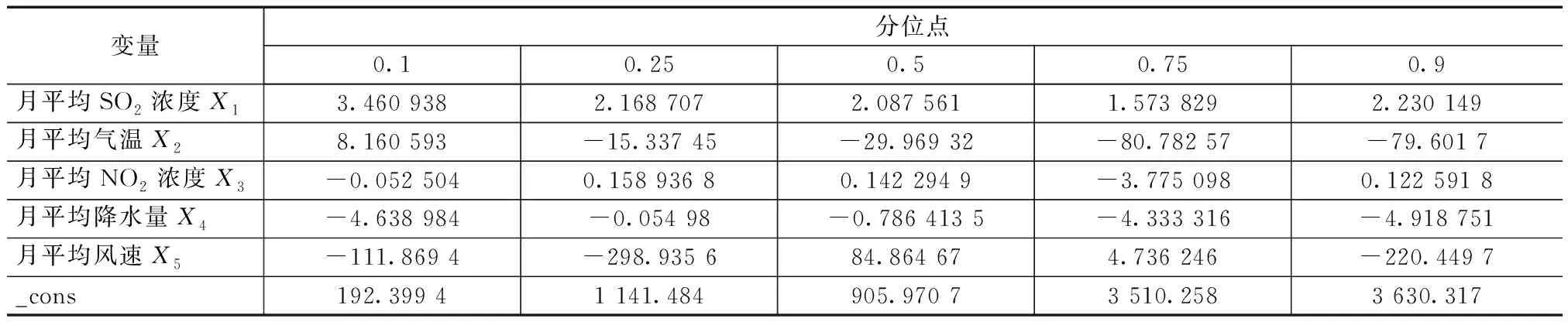
表8 线性分位数回归系数

0.1分位点下：

0.25分位点下：

0.5分位点下：

0.75分位点下：

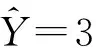
0.9分位点下：

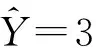
对不同分位点下的各个变量对月平均PM2.5浓度的影响建立的线性分位数回归模型进行显著性检验，具体结果见表9。

表9 系数检验

根据表9可以看出，在不同分位点上不同变量对月平均PM2.5的影响的显著性并不相同。在0.1分位点时月平均SO2浓度(X1)与月平均气温(X2)对月平均PM2.5浓度的影响都是显著的且月平均气温(X2)对PM2.5浓度的影响要比月平均SO2浓度(X1)要明显。

在0.25分位点时，月平均NO2浓度(X3)与月平均风速(X5)均对月平均PM2.5的浓度有显著影响且月平均NO2浓度(X3)比月平均风速(X5)对月平均PM2.5浓度的影响更为明显。

在0.5分位点时只有月平均SO2浓度(X1)对月平均PM2.5的浓度影响是显著的。这说明在0.5分位点时，只有月平均SO2的浓度(X1)显著影响着月平均PM2.5的浓度。

在0.75分位点上只有月平均气温(X2)与月平均降水量(X4)对月平均PM2.5浓度的影响是显著的且月平均气温(X2)比月平均降水量(X4)对月平均PM2.5的浓度影响更加显著。

在0.9分位点时只有月平均气温(X2)与月平均降水量(X4)对月平均PM2.5浓度的影响是显著的且月平均气温(X2)比月平均降水量(X4)对月平均PM2.5的浓度影响更加显著。

通过普通多元回归模型和分位数回归模型的检验结果都可以看出，月平均SO2浓度(X1)对空气中PM2.5的浓度影响都是很显著的。对比表4可以看出，在分位数回归模型中各因素可能会在不同的分位点上显示出显著性的特点，而普通的回归模型中只有一个变量显著，因此相比之下，分位数回归模型更加合理。

3.3 分位数回归与多元回归模型的比较

从上述的比较分析中可以看出，普通多元线性回归模型与分位数回归模型相比较来看，分位数回归模型较为宽松得到的信息量更加多。它不仅可以分析出各个因素的变化情况，还能看出不同分位点上的不同的影响即趋势性的变化情况。特别当误差为非正态分布时，分位数回归模型比普通多元模型有效，因此它弥补了最小二乘回归的不足。

首先进行普通的多元线性回归，在回归过程中发现不同变量的显著性特点也能正确地分析出各个变量对于所求变量的影响以及相关关系，得到了一个总的分析概括。然后，在数据整理过程中大多数的数据无法通过检验，变量也十分不显著，因此又建立了分位数回归模型，完成了线性分位数回归的拟合。可以看出，分位数回归模型相比较与普通多元回归模型更好，问题也更加明显和具体化，可以更加直观并且可以更加明白地得到不同分位点下的各个变量的显著性特点，也更能具体地分析得到该变量的详细变化趋势以及它在不同分位点下对所求变量的影响，以及各个分位点下的线性关系以及趋势性变化，对变量与所求变量间的关系更加明确清晰。

4 结论

选择月平均SO2浓度与月平均气温，构建了普通多元线性回归模型用来分析月平均SO2浓度与月平均气温对于月均PM2.5浓度的影响，建立回归方程，观察它们是否显著是否构建合理模型。与此同时构建了线性分位数回归模型，用于比较了在不同分位点上各个变量对不同浓度的PM2.5的影响大小的不同以及变化规律和变化程度，分析不同月份、不同季度PM2.5浓度的差异。构成成分的不同空气的流动速度不同众多因素的共同作用、共同影响造成了不同分位点下PM2.5的浓度不尽相同。SO2对PM2.5的浓度影响可以看作一个类似于二次函数的分布形式，在中间达到峰值，而在不同分位点上的显著性不同，会有不同的差异。

而月平均气温在各分位点上系数与显著性不能一并回答，因为月平均气温在对空气中PM2.5的浓度影响在不同分位点的表现并没有特殊分布。在某几个分位点展现出负向影响，而在个别分位点显出正向影响。

空气中存在的物质不同，所以也并非全部都表现出线性关系。因为受着多种因素的影响和相互作用，不同分位点下的因素也会不完全相同，因此不同的分位点下不同因素对空气中PM2.5浓度的变化影响也不同。

总之，即使是相同的影响因素也会在各个分位点对不同浓度的PM2.5浓度产生较大的影响差异，这具体表现在PM2.5浓度在不同月份里存在明显的差异上。

普通的多元回归只能得到月平均SO2浓度与月平均气温对月平均PM2.5浓度都是有显著性影响的。而在做分位数回归分析时发现，其实在某些分位点下,月平均SO2浓度与月平均气温是不显著的，比如月平均SO2浓度只在0.1分位点时是显著影响的，而同样可以看出，月平均气温在0.75与0.9分位点时对月平均PM2.5浓度的影响是不显著的。所以分位数回归模型要比普通多元回归模型更加清晰，也使分析更加准确。